北京课改版数学九年级上册同步课时练习:20.5 第2课时 坡度与解直角三角形(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级上册同步课时练习:20.5 第2课时 坡度与解直角三角形(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 192.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览



文档简介
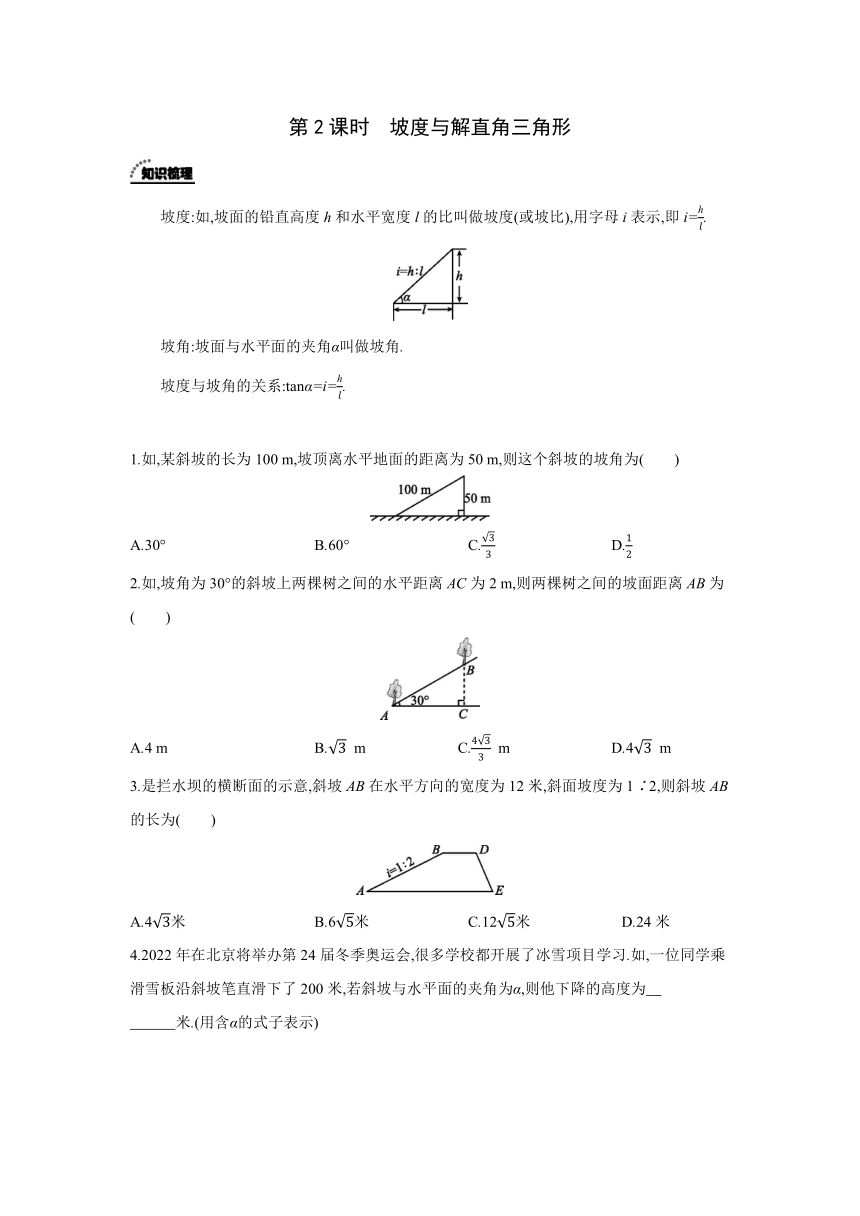
第2课时 坡度与解直角三角形
坡度:如,坡面的铅直高度h和水平宽度l的比叫做坡度(或坡比),用字母i表示,即i=.
坡角:坡面与水平面的夹角α叫做坡角.
坡度与坡角的关系:tanα=i=.
1.如,某斜坡的长为100 m,坡顶离水平地面的距离为50 m,则这个斜坡的坡角为( )
A.30° B.60° C. D.
2.如,坡角为30°的斜坡上两棵树之间的水平距离AC为2 m,则两棵树之间的坡面距离AB为( )
A.4 m B. m C. m D.4 m
3.是拦水坝的横断面的示意,斜坡AB在水平方向的宽度为12米,斜面坡度为1∶2,则斜坡AB的长为( )
A.4米 B.6米 C.12米 D.24米
4.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如,一位同学乘滑雪板沿斜坡笔直滑下了200米,若斜坡与水平面的夹角为α,则他下降的高度为
米.(用含α的式子表示)
5.[2019·石景山区期末] 如,某中学综合楼入口处有两级台阶,台阶高AD=BE=15 cm,宽DE=30 cm,在台阶处加装一段斜坡作为无障碍通道,设台阶起点为A,斜坡的起点为C,若斜坡CB的坡度i=1∶9,则AC的长为 cm.
6.北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.是某滑雪场为初学者练习用的斜坡示意,出于安全因素考虑,决定将斜坡AB的倾角由45°降为30°,已知原斜坡坡面AB的长为200米,求改善后的斜坡坡角向前推进的距离BD.(结果精确到1米.参考数据:≈1.41,≈1.73,≈2.45)
7.如,小阳发现电线杆AB在太阳光下的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,斜坡CD的坡度为1∶,且此时测得1米长的木杆在太阳光下的影长为2米,则电线杆的高度为( )
A.9米 B.28米 C.(7+)米 D.(14+2)米
8.响应“绿色环保,畅通出行”的号召,越来越多的市民选择乘地铁出行,为保证市民方便出行,我市新建了多条地铁线路,与旧地铁线路相比,新建地铁车站出入口上下楼梯的高度普遍增加.如,已知原楼梯BD长20米,在楼梯水平长度(BC)不发生改变的前提下,楼梯的倾斜角由30°增大到45°,那么新修建的楼梯AB高度将会增加多少米 (结果精确到1米.参考数据:≈1.414,≈1.732)
9.如(②为①的示意),要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α要满足60°≤α≤75°,现有一架长AB=5.5 m的梯子.
(1)使用这架梯子最高可以安全攀上多高的墙(结果精确到0.1 m)
(2)当梯子底端到墙面的距离BC=2.2 m时,α等于多少度(结果精确到0.1°) 此时人是否能够安全使用这架梯子 (参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,sin23.6°≈0.40,cos66.4°≈0.40,tan21.8°≈0.40)
10.缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如,当缆车从点A到达点B时,它走过了700米.由点B到达山顶点D时,它又走过了700米.已知线路AB与水平线的夹角α为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计,写出解题思路即可).
答案
1.A 2.C
3.B 解: 过点B作BC⊥AE于点C.
在Rt△ABC中,
∵=i=,AC=12米,∴BC=6米.
在Rt△ABC中,根据勾股定理,得
AB==6(米).故选B.
4.200sinα
5.240 解: 如,过点B作BF⊥AC于点F.由题可知BF=30 cm,AF=30 cm.
∵tan∠BCA==,∴CF=270 cm,
∴AC=CF-AF=270-30=240(cm).
6.解:过点A作AC⊥BD于点C.在Rt△ABC中,∠ACB=90°,∠ABC=45°,AB=200米,
∴AC=BC=AB·sin∠ABC=200×sin45°=100(米).
∵在Rt△ACD中,∠ACD=90°,∠D=30°,
∴CD===100(米),
∴BD=CD-BC=100-100≈104(米).
答:改善后的斜坡坡角向前推进的距离BD约为104米.
7.D 解: 延长AD交BC的延长线于点F,过点D作DE⊥BF于点E.
∵斜坡CD的坡度为1∶,∴∠DCE=30°.
又∵CD=8米,
∴DE=4米,CE=CD·cos∠DCE=8×=4(米),设AB=x米,EF=y米.
∵DE⊥BF,AB⊥BF,
∴∠DEF=∠ABC=90°.
又∵∠F=∠F,∴△DEF∽△ABF,
∴=,即=…①.
∵1米长的木杆的影长为2米,根据同一时间物高与影长成正比可得=…②,
①②联立,解得x=(14+2)米.
8.解:由题意,可得△ABC和△BDC都是直角三角形.
在Rt△BDC中,BD=20,∠DBC=30°,
∴CD=10,BC=BD·cos∠DBC=20×=10.
在Rt△ABC中,∠ABC=45°.
∴AC=BC=10.
∴AD=AC-CD=(10-10)米.
∴AD≈10×1.732-10≈7(米).
答:新修建的楼梯AB高度将会增加约7米.
9.解:(1)由题意,得当α=75°时,这架梯子可以安全攀上的墙最高.
在Rt△ABC中,sinα=,
∴AC=AB·sinα,
∴AC最大为AB·sin75°≈5.5×0.97≈5.3(m).
答:使用这架梯子最高可以安全攀上约5.3 m的墙.
(2)在Rt△ABC中,cosα===0.4,
则α≈66.4°.
∵60°<66.4°<75°,
∴此时人能够安全使用这架梯子.
10.解:设计如.由题意可得,∠DEB=90°,四边形BCFE,四边形AGHF均为矩形.在Rt△ABC中,∠ACB=90°,α=16°,AB=700,由sinα,可求BC的长.
即BC=AB·sinα=700sin16°.
在Rt△BDE中,∠DEB=90°,β=20°,BD=700,由sinβ,可求DE的长.
即DE=BD·sinβ=700sin20°.
由矩形的性质,可知EF=BC=700sin16°,
FH=AG=126.
从而,可求得DH的长.
即DH=DE+EF+FH=(700sin20°+700sin16°+126)米.
坡度:如,坡面的铅直高度h和水平宽度l的比叫做坡度(或坡比),用字母i表示,即i=.
坡角:坡面与水平面的夹角α叫做坡角.
坡度与坡角的关系:tanα=i=.
1.如,某斜坡的长为100 m,坡顶离水平地面的距离为50 m,则这个斜坡的坡角为( )
A.30° B.60° C. D.
2.如,坡角为30°的斜坡上两棵树之间的水平距离AC为2 m,则两棵树之间的坡面距离AB为( )
A.4 m B. m C. m D.4 m
3.是拦水坝的横断面的示意,斜坡AB在水平方向的宽度为12米,斜面坡度为1∶2,则斜坡AB的长为( )
A.4米 B.6米 C.12米 D.24米
4.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如,一位同学乘滑雪板沿斜坡笔直滑下了200米,若斜坡与水平面的夹角为α,则他下降的高度为
米.(用含α的式子表示)
5.[2019·石景山区期末] 如,某中学综合楼入口处有两级台阶,台阶高AD=BE=15 cm,宽DE=30 cm,在台阶处加装一段斜坡作为无障碍通道,设台阶起点为A,斜坡的起点为C,若斜坡CB的坡度i=1∶9,则AC的长为 cm.
6.北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.是某滑雪场为初学者练习用的斜坡示意,出于安全因素考虑,决定将斜坡AB的倾角由45°降为30°,已知原斜坡坡面AB的长为200米,求改善后的斜坡坡角向前推进的距离BD.(结果精确到1米.参考数据:≈1.41,≈1.73,≈2.45)
7.如,小阳发现电线杆AB在太阳光下的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,斜坡CD的坡度为1∶,且此时测得1米长的木杆在太阳光下的影长为2米,则电线杆的高度为( )
A.9米 B.28米 C.(7+)米 D.(14+2)米
8.响应“绿色环保,畅通出行”的号召,越来越多的市民选择乘地铁出行,为保证市民方便出行,我市新建了多条地铁线路,与旧地铁线路相比,新建地铁车站出入口上下楼梯的高度普遍增加.如,已知原楼梯BD长20米,在楼梯水平长度(BC)不发生改变的前提下,楼梯的倾斜角由30°增大到45°,那么新修建的楼梯AB高度将会增加多少米 (结果精确到1米.参考数据:≈1.414,≈1.732)
9.如(②为①的示意),要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α要满足60°≤α≤75°,现有一架长AB=5.5 m的梯子.
(1)使用这架梯子最高可以安全攀上多高的墙(结果精确到0.1 m)
(2)当梯子底端到墙面的距离BC=2.2 m时,α等于多少度(结果精确到0.1°) 此时人是否能够安全使用这架梯子 (参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,sin23.6°≈0.40,cos66.4°≈0.40,tan21.8°≈0.40)
10.缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如,当缆车从点A到达点B时,它走过了700米.由点B到达山顶点D时,它又走过了700米.已知线路AB与水平线的夹角α为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计,写出解题思路即可).
答案
1.A 2.C
3.B 解: 过点B作BC⊥AE于点C.
在Rt△ABC中,
∵=i=,AC=12米,∴BC=6米.
在Rt△ABC中,根据勾股定理,得
AB==6(米).故选B.
4.200sinα
5.240 解: 如,过点B作BF⊥AC于点F.由题可知BF=30 cm,AF=30 cm.
∵tan∠BCA==,∴CF=270 cm,
∴AC=CF-AF=270-30=240(cm).
6.解:过点A作AC⊥BD于点C.在Rt△ABC中,∠ACB=90°,∠ABC=45°,AB=200米,
∴AC=BC=AB·sin∠ABC=200×sin45°=100(米).
∵在Rt△ACD中,∠ACD=90°,∠D=30°,
∴CD===100(米),
∴BD=CD-BC=100-100≈104(米).
答:改善后的斜坡坡角向前推进的距离BD约为104米.
7.D 解: 延长AD交BC的延长线于点F,过点D作DE⊥BF于点E.
∵斜坡CD的坡度为1∶,∴∠DCE=30°.
又∵CD=8米,
∴DE=4米,CE=CD·cos∠DCE=8×=4(米),设AB=x米,EF=y米.
∵DE⊥BF,AB⊥BF,
∴∠DEF=∠ABC=90°.
又∵∠F=∠F,∴△DEF∽△ABF,
∴=,即=…①.
∵1米长的木杆的影长为2米,根据同一时间物高与影长成正比可得=…②,
①②联立,解得x=(14+2)米.
8.解:由题意,可得△ABC和△BDC都是直角三角形.
在Rt△BDC中,BD=20,∠DBC=30°,
∴CD=10,BC=BD·cos∠DBC=20×=10.
在Rt△ABC中,∠ABC=45°.
∴AC=BC=10.
∴AD=AC-CD=(10-10)米.
∴AD≈10×1.732-10≈7(米).
答:新修建的楼梯AB高度将会增加约7米.
9.解:(1)由题意,得当α=75°时,这架梯子可以安全攀上的墙最高.
在Rt△ABC中,sinα=,
∴AC=AB·sinα,
∴AC最大为AB·sin75°≈5.5×0.97≈5.3(m).
答:使用这架梯子最高可以安全攀上约5.3 m的墙.
(2)在Rt△ABC中,cosα===0.4,
则α≈66.4°.
∵60°<66.4°<75°,
∴此时人能够安全使用这架梯子.
10.解:设计如.由题意可得,∠DEB=90°,四边形BCFE,四边形AGHF均为矩形.在Rt△ABC中,∠ACB=90°,α=16°,AB=700,由sinα,可求BC的长.
即BC=AB·sinα=700sin16°.
在Rt△BDE中,∠DEB=90°,β=20°,BD=700,由sinβ,可求DE的长.
即DE=BD·sinβ=700sin20°.
由矩形的性质,可知EF=BC=700sin16°,
FH=AG=126.
从而,可求得DH的长.
即DH=DE+EF+FH=(700sin20°+700sin16°+126)米.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
