北京课改版数学九年级上册同步课时练习:21.3 第1课时 圆的轴对称性 (word版含答案)
文档属性
| 名称 | 北京课改版数学九年级上册同步课时练习:21.3 第1课时 圆的轴对称性 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 07:04:14 | ||
图片预览



文档简介
二 21.3 第1课时 圆的轴对称性
1.圆的轴对称性
圆是轴对称形,它有无数条对称轴,经过圆心的每一条直线都是它的对称轴.
2.垂径定理及其推论
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
强调: 下列五个条件:①直径(过圆心的线段);②垂直于弦;③平分弦(不是直径);④平分弦所对的优弧;⑤平分弦所对的劣弧.以其中的两个为条件,一定能得出其他三个结论.
1.下列命题错误的是 ( )
A.平分弧的直径平分这条弧所对的弦
B.平分弦的直径平分这条弦所对的弧
C.垂直于弦的直径平分这条弦
D.弦的垂直平分线经过圆心
2.如DC是☉O的直径,弦AB⊥CD,垂足为M,则下列等式不一定成立的是 ( )
A.CM=DM B.AM=BM C. = D. =
3.[2020·西城区期中] 如AB为☉O的弦,C为AB的中点,AB=8,OC=3,则☉O的半径为 ( )
A.4 B.5 C.6 D.7
4.过☉O内一点M的最长弦长为10 cm,最短弦长为8 cm,则OM的长为 ( )
A.9 cm B.6 cm C.3 cm D. cm
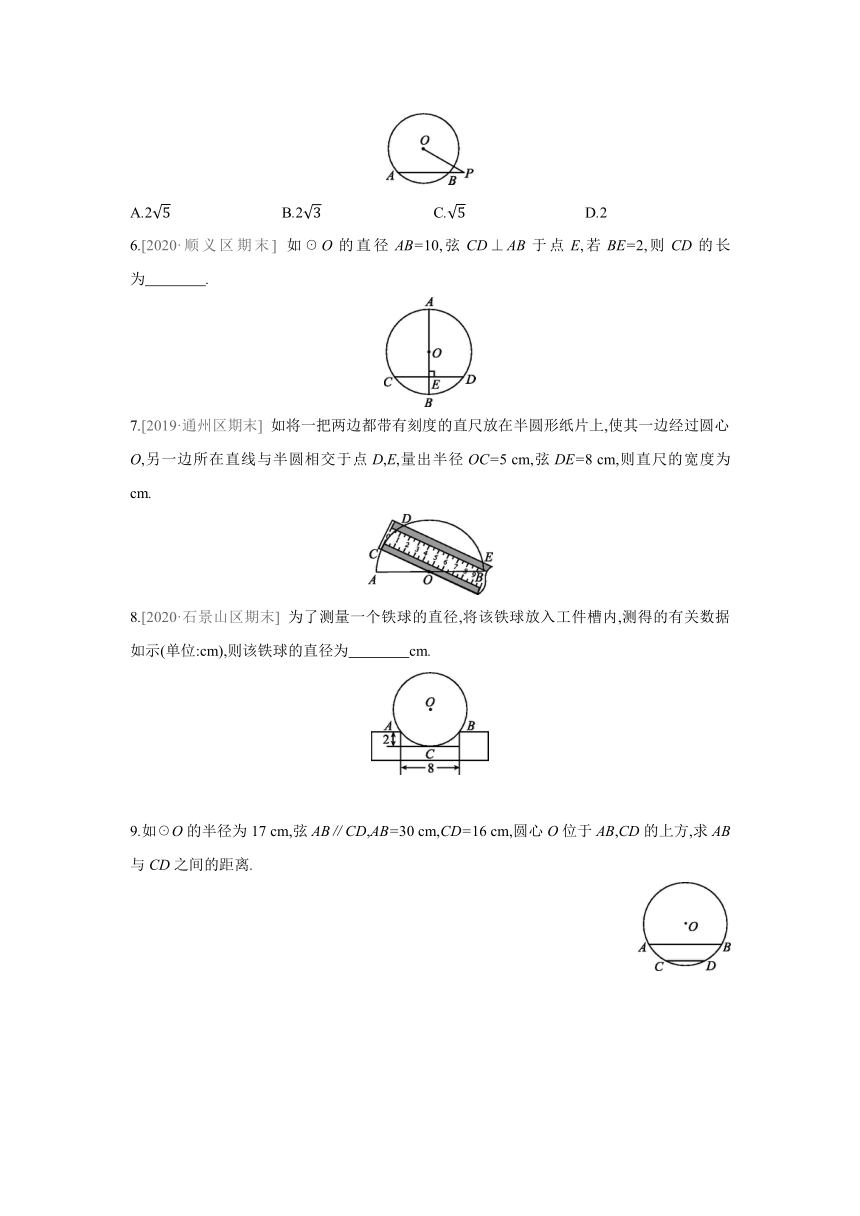
5.如☉O的半径为3,P是弦AB延长线上的一点,连接OP,若OP=4,∠P=30°,则弦AB的长为 ( )
A.2 B.2 C. D.2
6.[2020·顺义区期末] 如☉O的直径AB=10,弦CD⊥AB于点E,若BE=2,则CD的长为 .
7.[2019·通州区期末] 如将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5 cm,弦DE=8 cm,则直尺的宽度为 cm.
8.[2020·石景山区期末] 为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如示(单位:cm),则该铁球的直径为 cm.
9.如☉O的半径为17 cm,弦AB∥CD,AB=30 cm,CD=16 cm,圆心O位于AB,CD的上方,求AB与CD之间的距离.
10.已知:如☉O的直径AB与弦CD(不是直径)交于点F,若FB=2,CF=FD=4,求AC的长.
11.已知☉O的直径CD=10 cm,AB是☉O的弦,AB⊥CD,垂足为M,且AB=8 cm,则AC的长为( )
A.2 cm B.4 cm
C.4 cm或2 cm D.4 cm或2 cm
12.如圆弧形桥拱的跨度AB=16 m,拱高CD=4 m,则圆弧形桥拱所在圆的半径为 ( )
A.6 m B.8 m C.10 m D.12 m
13.[2020·石景山区一模] 《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”其意思是:如,AB为☉O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸 (注:1尺=10寸)根据题意,知该圆的直径为
寸.
14.如,在平面直角坐标系中,O为坐标原点,点P在第一象限内,☉P与x轴交于O,A两点,点A的坐标为(6,0),☉P的半径为,则点P的坐标为 .
15.[2020·昌平区期末] 如,一条公路的转弯处是一段圆弧,O是这段弧所在圆的圆心.AB=100 m,C是上一点,OC⊥AB,垂足为D,CD=10 m,求这段弯路的半径.
16.如,M为☉O内任意一点,AB为过点M且和OM垂直的一条弦,CD为过点M的任意一条弦(不与弦AB重合).
(1)求证:AB(2)在过点M的所有弦中,有没有最长的弦 (填“有”或“没有”).有没有最短的弦 (填“有”或“没有”).如果有,最长的弦与OM的位置关系为 ,最短的弦与OM的位置关系为 ;
(3)如果过点M的所有弦中,最长的弦是EF,最短的弦是GH,且EF=26,GH=24,求OM的长.
答案
1.B 2.A 3.B 4.C
5.A 解: 如,过点O作OH⊥AB于点H,连接OA.
在Rt△OHP中,OP=4,∠P=30°,则OH=2.
在Rt△OHA中,OH=2,OA=3,则由勾股定理,得AH==,则AB=2AH=2.
6.8
7.3 解: 过点O作OM⊥DE于点M,连接OD,则DM=DE.∵DE=8 cm,∴DM=4 cm.在Rt△ODM中,∵OD=OC=5 cm,
∴OM2=OD2-DM2,则OM=3 cm,
∴直尺的宽度为3 cm.
8.10
9.解:如,过点O作OE⊥AB,交AB于点E,交CD于点F,连接OA,OC.
∵AB∥CD,∴OF⊥CD.
在Rt△OAE中,
∵OA=17 cm,AE=BE=AB=15 cm,
∴OE==8(cm),
同理可求OF==15(cm).
∵圆心O位于AB,CD的上方,
∴EF=OF-OE=15-8=7(cm),
即AB与CD之间的距离是7 cm.
10.解:连接OD.
设☉O的半径为R.
∵AB是☉O的直径,且CF=FD,
∴AB⊥CD.
∵OB=R,FB=2,
∴OF=R-2.
在Rt△OFD中,
由勾股定理,得R2=(R-2)2+42,
解得R=5,∴AF=8.
在Rt△ACF中,
由勾股定理,得AC==4.
11.C 解: 先根据题意画出形,因为点C的位置不能确定,所以应分两种情况进行讨论.
连接AC,AO.
∵☉O的直径CD=10 cm,AB⊥CD,AB=8 cm,
∴AM=MB=×8=4(cm),OD=OC=5 cm.
当点C的位置如①所示时,
∵OA=5 cm,AM=4 cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当点C的位置如②所示时,同理可得OM=3 cm.∵OC=5 cm,∴MC=5-3=2(cm).
在Rt△AMC中,AC===2(cm).
综上可知,AC的长为4 cm或2 cm.
12.C 解: 如,设OA=r m,则OD=(r-4)m.
∵AB=16 m,
∴AD=8 m.
在Rt△AOD中,
OD2+AD2=OA2,即(r-4)2+82=r2,解得r=10.
故选C.
13.26 解: 如,连接OC.
∵弦CD⊥AB,AB为☉O的直径,
∴E为CD的中点.
又∵CD=1尺=10寸,
∴CE=DE=CD=5寸.
设OC=OA=x寸,则AB=2x寸,OE=(x-1)寸.
由勾股定理,得OE2+CE2=OC2,
即(x-1)2+52=x2,
解得x=13,
∴AB=26寸,
即直径AB的长为26寸.
14.(3,2) 解: 如,过点P作PD⊥x轴于点D,连接OP.
∵A(6,0),PD⊥OA,
∴OD=DA=3.
在Rt△OPD中,
∵OP=,OD=3,
∴PD===2,
∴点P的坐标为(3,2).
15.解:设这段弯路的半径为r m.
∵OC⊥AB于点D,AB=100 m,
∴BD=DA=AB=50 m.
∵CD=10 m,∴OD=(r-10)m.
在Rt△BOD中,根据勾股定理,得BO2=BD2+OD2,即r2=502+(r-10)2,
解得r=130(m).
答:这段弯路的半径为130 m.
16.解:(1)证明:如所示,过点O作ON⊥CD,垂足为N,连接OB,OD,
则AB=2BM,CD=2DN.
设OB=OD=R.
在Rt△BOM中,
BM==.
在Rt△DON中,
DN==.
在Rt△MON中,
∵OM是斜边,ON是直角边,
∴OM >ON,
∴R2-OM2即BM(2)有 有 在一条直线上 互相垂直
(3)OM====5.
1.圆的轴对称性
圆是轴对称形,它有无数条对称轴,经过圆心的每一条直线都是它的对称轴.
2.垂径定理及其推论
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
强调: 下列五个条件:①直径(过圆心的线段);②垂直于弦;③平分弦(不是直径);④平分弦所对的优弧;⑤平分弦所对的劣弧.以其中的两个为条件,一定能得出其他三个结论.
1.下列命题错误的是 ( )
A.平分弧的直径平分这条弧所对的弦
B.平分弦的直径平分这条弦所对的弧
C.垂直于弦的直径平分这条弦
D.弦的垂直平分线经过圆心
2.如DC是☉O的直径,弦AB⊥CD,垂足为M,则下列等式不一定成立的是 ( )
A.CM=DM B.AM=BM C. = D. =
3.[2020·西城区期中] 如AB为☉O的弦,C为AB的中点,AB=8,OC=3,则☉O的半径为 ( )
A.4 B.5 C.6 D.7
4.过☉O内一点M的最长弦长为10 cm,最短弦长为8 cm,则OM的长为 ( )
A.9 cm B.6 cm C.3 cm D. cm
5.如☉O的半径为3,P是弦AB延长线上的一点,连接OP,若OP=4,∠P=30°,则弦AB的长为 ( )
A.2 B.2 C. D.2
6.[2020·顺义区期末] 如☉O的直径AB=10,弦CD⊥AB于点E,若BE=2,则CD的长为 .
7.[2019·通州区期末] 如将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5 cm,弦DE=8 cm,则直尺的宽度为 cm.
8.[2020·石景山区期末] 为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如示(单位:cm),则该铁球的直径为 cm.
9.如☉O的半径为17 cm,弦AB∥CD,AB=30 cm,CD=16 cm,圆心O位于AB,CD的上方,求AB与CD之间的距离.
10.已知:如☉O的直径AB与弦CD(不是直径)交于点F,若FB=2,CF=FD=4,求AC的长.
11.已知☉O的直径CD=10 cm,AB是☉O的弦,AB⊥CD,垂足为M,且AB=8 cm,则AC的长为( )
A.2 cm B.4 cm
C.4 cm或2 cm D.4 cm或2 cm
12.如圆弧形桥拱的跨度AB=16 m,拱高CD=4 m,则圆弧形桥拱所在圆的半径为 ( )
A.6 m B.8 m C.10 m D.12 m
13.[2020·石景山区一模] 《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”其意思是:如,AB为☉O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸 (注:1尺=10寸)根据题意,知该圆的直径为
寸.
14.如,在平面直角坐标系中,O为坐标原点,点P在第一象限内,☉P与x轴交于O,A两点,点A的坐标为(6,0),☉P的半径为,则点P的坐标为 .
15.[2020·昌平区期末] 如,一条公路的转弯处是一段圆弧,O是这段弧所在圆的圆心.AB=100 m,C是上一点,OC⊥AB,垂足为D,CD=10 m,求这段弯路的半径.
16.如,M为☉O内任意一点,AB为过点M且和OM垂直的一条弦,CD为过点M的任意一条弦(不与弦AB重合).
(1)求证:AB
(3)如果过点M的所有弦中,最长的弦是EF,最短的弦是GH,且EF=26,GH=24,求OM的长.
答案
1.B 2.A 3.B 4.C
5.A 解: 如,过点O作OH⊥AB于点H,连接OA.
在Rt△OHP中,OP=4,∠P=30°,则OH=2.
在Rt△OHA中,OH=2,OA=3,则由勾股定理,得AH==,则AB=2AH=2.
6.8
7.3 解: 过点O作OM⊥DE于点M,连接OD,则DM=DE.∵DE=8 cm,∴DM=4 cm.在Rt△ODM中,∵OD=OC=5 cm,
∴OM2=OD2-DM2,则OM=3 cm,
∴直尺的宽度为3 cm.
8.10
9.解:如,过点O作OE⊥AB,交AB于点E,交CD于点F,连接OA,OC.
∵AB∥CD,∴OF⊥CD.
在Rt△OAE中,
∵OA=17 cm,AE=BE=AB=15 cm,
∴OE==8(cm),
同理可求OF==15(cm).
∵圆心O位于AB,CD的上方,
∴EF=OF-OE=15-8=7(cm),
即AB与CD之间的距离是7 cm.
10.解:连接OD.
设☉O的半径为R.
∵AB是☉O的直径,且CF=FD,
∴AB⊥CD.
∵OB=R,FB=2,
∴OF=R-2.
在Rt△OFD中,
由勾股定理,得R2=(R-2)2+42,
解得R=5,∴AF=8.
在Rt△ACF中,
由勾股定理,得AC==4.
11.C 解: 先根据题意画出形,因为点C的位置不能确定,所以应分两种情况进行讨论.
连接AC,AO.
∵☉O的直径CD=10 cm,AB⊥CD,AB=8 cm,
∴AM=MB=×8=4(cm),OD=OC=5 cm.
当点C的位置如①所示时,
∵OA=5 cm,AM=4 cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当点C的位置如②所示时,同理可得OM=3 cm.∵OC=5 cm,∴MC=5-3=2(cm).
在Rt△AMC中,AC===2(cm).
综上可知,AC的长为4 cm或2 cm.
12.C 解: 如,设OA=r m,则OD=(r-4)m.
∵AB=16 m,
∴AD=8 m.
在Rt△AOD中,
OD2+AD2=OA2,即(r-4)2+82=r2,解得r=10.
故选C.
13.26 解: 如,连接OC.
∵弦CD⊥AB,AB为☉O的直径,
∴E为CD的中点.
又∵CD=1尺=10寸,
∴CE=DE=CD=5寸.
设OC=OA=x寸,则AB=2x寸,OE=(x-1)寸.
由勾股定理,得OE2+CE2=OC2,
即(x-1)2+52=x2,
解得x=13,
∴AB=26寸,
即直径AB的长为26寸.
14.(3,2) 解: 如,过点P作PD⊥x轴于点D,连接OP.
∵A(6,0),PD⊥OA,
∴OD=DA=3.
在Rt△OPD中,
∵OP=,OD=3,
∴PD===2,
∴点P的坐标为(3,2).
15.解:设这段弯路的半径为r m.
∵OC⊥AB于点D,AB=100 m,
∴BD=DA=AB=50 m.
∵CD=10 m,∴OD=(r-10)m.
在Rt△BOD中,根据勾股定理,得BO2=BD2+OD2,即r2=502+(r-10)2,
解得r=130(m).
答:这段弯路的半径为130 m.
16.解:(1)证明:如所示,过点O作ON⊥CD,垂足为N,连接OB,OD,
则AB=2BM,CD=2DN.
设OB=OD=R.
在Rt△BOM中,
BM==.
在Rt△DON中,
DN==.
在Rt△MON中,
∵OM是斜边,ON是直角边,
∴OM >ON,
∴R2-OM2
(3)OM====5.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
