北京课改版数学九年级下册 23.2 第1课时 旋转及其性质 同步课时练习(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级下册 23.2 第1课时 旋转及其性质 同步课时练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 325.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览


文档简介
23.2 第1课时 旋转及其性质
1.在平面内,将一个形绕一个定点沿顺时针或逆时针方向转动一个角度,得到一个新的形,这样的形运动称为旋转变换,简称旋转,这个定点称为旋转中心,转动的角称为旋转角.如果形上的点P经过旋转到点P',那么这两个点叫做旋转的对应点.
2.性质:(1)任意一对对应点与旋转中心的连线所成的角都是旋转角;(2)对应点到旋转中心的距离相等;(3)旋转前后的形全等.
3.旋转作的一般步骤:(1)分析题目要求,找出旋转中心、旋转角、旋转方向;(2)分析形,找出构成原形的关键点;(3)沿一定的方向,按一定的角度,旋转各个关键点,得到其对应点;(4)连接所作的各个关键点的对应点,并标上相应字母;(5)写出结论.
1.下列现象不属于旋转的是 ( )
A.摩托车在急刹车时向前滑动
B.汽车在行驶过程中车轮的运动
C.拧开自来水水龙头的过程
D.光盘在播放过程中的运动
2.在旋转过程中,确定一个三角形旋转后的位置所需的条件是 ( )
①三角形原来的位置;②旋转中心;③三角形的形状;④旋转角;⑤旋转方向.
A.①②④⑤ B.①②③⑤
C.②③④⑤ D.①③④⑤
3.一个形经旋转变换后,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④形的形状和大小都没有发生变化.其中正确的是( )
A.①②③ B.①②④
C.①③④ D.②③④
4.[2020·西城区期末] 如在△ABC中,以C为中心,将△ABC顺时针旋转35°得到△DEC,边ED,AC相交于点F,若∠A=30°,则∠EFC的度数为( )
A.60° B.65° C.72.5° D.115°
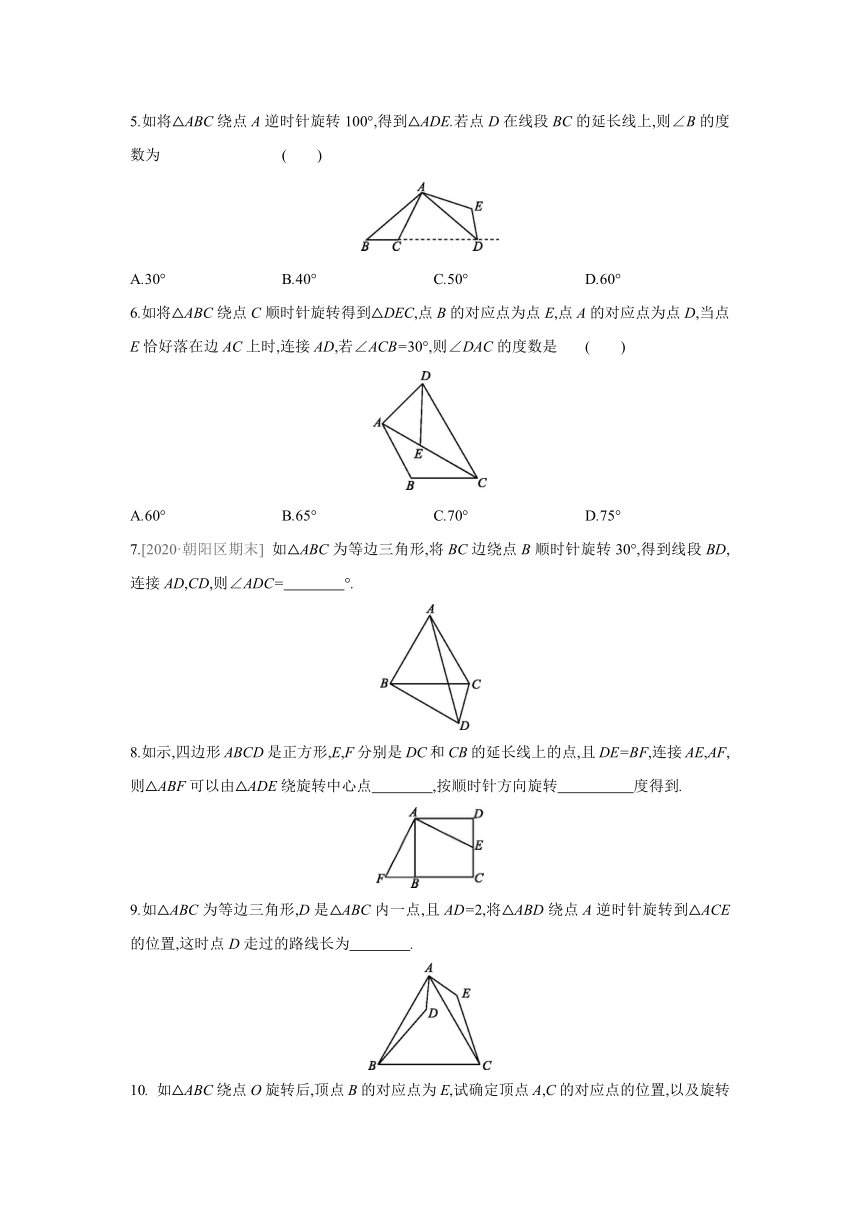
5.如将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的度数为 ( )
A.30° B.40° C.50° D.60°
6.如将△ABC绕点C顺时针旋转得到△DEC,点B的对应点为点E,点A的对应点为点D,当点E恰好落在边AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是 ( )
A.60° B.65° C.70° D.75°
7.[2020·朝阳区期末] 如△ABC为等边三角形,将BC边绕点B顺时针旋转30°,得到线段BD,连接AD,CD,则∠ADC= °.
8.如示,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,则△ABF可以由△ADE绕旋转中心点 ,按顺时针方向旋转 度得到.
9.如△ABC为等边三角形,D是△ABC内一点,且AD=2,将△ABD绕点A逆时针旋转到△ACE的位置,这时点D走过的路线长为 .
10. 如△ABC绕点O旋转后,顶点B的对应点为E,试确定顶点A,C的对应点的位置,以及旋转后的三角形.
11.如C是线段BD上一点,分别以BC,CD为边在BD同侧作等边三角形ABC和等边三角形CDE,AD交CE于点F,BE交AC于点G,写出中可通过旋转而相互得到的三角形并说明理由(要求把符合条件的都写出来).
12.在如示的形中,是由一个矩形沿顺时针方向旋转90°后所形成的形的是 ( )
A.①④ B.②③ C.①② D.②④
13.如,已知正方形ABCD的边长是2,如果将线段BD绕点B旋转后,点D落在CB的延长线上的点D'处,那么tan∠BAD'等于 ( )
A.1 B. C. D.2
14.[2020·东城区期末] 如,在正方形网格中,将格点三角形ABC绕某点顺时针旋转角α(0°<α<180°)得到格点三角形A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点.
(1)请通过画找到旋转中心,将其标记为点O;
(2)直接写出旋转角α的度数.
15.如所示,P是等边三角形ABC内一点,且∠APB∶∠BPC∶∠CPA=3∶4∶5,求以PA,PB,PC为边的三角形的三个内角的度数.
16.如①,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.如②操作,固定△ABC,使△DEC绕点C按顺时针方向旋转,点D恰好落在AB边上.
(1)线段DE与AC的位置关系如何
(2)设△BDC的面积为S1,△AEC的面积为S2,则S1与S2具有怎样的数量关系
答案
1.A 2.A 3.D 4.B 5.B
6.D 7.30
8.A 90 解: 根据正方形的性质得AD=AB,∠D=∠ABF=90°,然后利用“SAS”易证得△ADE≌△ABF.又因为∠BAD=90°,所以根据旋转的定义可得△ABF可以由△ADE绕旋转中心点A按顺时针方向旋转90度得到.
9.π
10.解:如,点A的对应点为D,点C的对应点为F.△DEF是△ABC旋转后得到的三角形.
11.解:△ACD和△BCE,△FCD和△GCE,△ACF和△BCG.
理由如下:①∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,则∠BCE=∠ACD,∴△ACD≌△BCE,
∴△ACD绕点C逆时针旋转60°可得到△BCE.
②∵∠ACB=∠ECD=60°,
∴∠ACF=180°-60°-60°=60°.
又∵△ACD绕点C逆时针旋转60°可得到△BCE,
∴∠BEC=∠ADC,CE=CD.
又∵∠ACE=∠ECD,∴△FCD≌△GCE,
∴△FCD绕点C逆时针旋转60°可得到△GCE.
由①②易得△ACF绕点C逆时针旋转60°可得△BCG.
12.B 13.B
14.解:(1)如所示.
(2)如.α=∠AOA1=90°.
15.解:由题意知∠APB=90°,∠BPC=120°,∠CPA=150°.
如,把△APC绕点A顺时针旋转60°,使AC与AB重合,点P落在点P'处,连接PP',则△APP'为等边三角形,
∴PP'=PA,∠AP'P=∠APP'=60°.
∵P'B=PC,
∴△P'BP就是以PA,PB,PC为边的三角形.
∵∠BP'P=∠AP'B-∠AP'P=∠CPA-∠AP'P=150°-60°=90°,
∠BPP'=∠APB-∠APP'=90°-60°=30°,
∴∠P'BP=180°-∠BP'P-∠BPP'=60°.
故以PA,PB,PC为边的三角形的三个内角的度数分别为30°,60°,90°.
16.解:(1)由旋转可知AC=DC.
∵∠ACB=∠DCE=90°,∠B=∠CED=30°,
∴∠BAC=∠EDC=60°,∴△ADC是等边三角形,
则∠ACD=60°,∴∠ACD=∠EDC,∴DE∥AC.
(2)如,过点D作DN⊥AC于点N,过点E作EM⊥AC交AC的延长线于点M,过点C作CF⊥AB于点F,∴DN∥EM.
由(1)可知△ADC是等边三角形,DE∥AC,
∴DN=CF,四边形DNME为矩形,∴DN=EM,∴CF=EM.
∵∠ACB=90°,∠B=30°,∴AB=2AC.
又∵AD=AC,∴BD=AC.
又∵S1=CF·BD,S2=AC·EM,
∴S1=S2.
1.在平面内,将一个形绕一个定点沿顺时针或逆时针方向转动一个角度,得到一个新的形,这样的形运动称为旋转变换,简称旋转,这个定点称为旋转中心,转动的角称为旋转角.如果形上的点P经过旋转到点P',那么这两个点叫做旋转的对应点.
2.性质:(1)任意一对对应点与旋转中心的连线所成的角都是旋转角;(2)对应点到旋转中心的距离相等;(3)旋转前后的形全等.
3.旋转作的一般步骤:(1)分析题目要求,找出旋转中心、旋转角、旋转方向;(2)分析形,找出构成原形的关键点;(3)沿一定的方向,按一定的角度,旋转各个关键点,得到其对应点;(4)连接所作的各个关键点的对应点,并标上相应字母;(5)写出结论.
1.下列现象不属于旋转的是 ( )
A.摩托车在急刹车时向前滑动
B.汽车在行驶过程中车轮的运动
C.拧开自来水水龙头的过程
D.光盘在播放过程中的运动
2.在旋转过程中,确定一个三角形旋转后的位置所需的条件是 ( )
①三角形原来的位置;②旋转中心;③三角形的形状;④旋转角;⑤旋转方向.
A.①②④⑤ B.①②③⑤
C.②③④⑤ D.①③④⑤
3.一个形经旋转变换后,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④形的形状和大小都没有发生变化.其中正确的是( )
A.①②③ B.①②④
C.①③④ D.②③④
4.[2020·西城区期末] 如在△ABC中,以C为中心,将△ABC顺时针旋转35°得到△DEC,边ED,AC相交于点F,若∠A=30°,则∠EFC的度数为( )
A.60° B.65° C.72.5° D.115°
5.如将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的度数为 ( )
A.30° B.40° C.50° D.60°
6.如将△ABC绕点C顺时针旋转得到△DEC,点B的对应点为点E,点A的对应点为点D,当点E恰好落在边AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是 ( )
A.60° B.65° C.70° D.75°
7.[2020·朝阳区期末] 如△ABC为等边三角形,将BC边绕点B顺时针旋转30°,得到线段BD,连接AD,CD,则∠ADC= °.
8.如示,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,则△ABF可以由△ADE绕旋转中心点 ,按顺时针方向旋转 度得到.
9.如△ABC为等边三角形,D是△ABC内一点,且AD=2,将△ABD绕点A逆时针旋转到△ACE的位置,这时点D走过的路线长为 .
10. 如△ABC绕点O旋转后,顶点B的对应点为E,试确定顶点A,C的对应点的位置,以及旋转后的三角形.
11.如C是线段BD上一点,分别以BC,CD为边在BD同侧作等边三角形ABC和等边三角形CDE,AD交CE于点F,BE交AC于点G,写出中可通过旋转而相互得到的三角形并说明理由(要求把符合条件的都写出来).
12.在如示的形中,是由一个矩形沿顺时针方向旋转90°后所形成的形的是 ( )
A.①④ B.②③ C.①② D.②④
13.如,已知正方形ABCD的边长是2,如果将线段BD绕点B旋转后,点D落在CB的延长线上的点D'处,那么tan∠BAD'等于 ( )
A.1 B. C. D.2
14.[2020·东城区期末] 如,在正方形网格中,将格点三角形ABC绕某点顺时针旋转角α(0°<α<180°)得到格点三角形A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点.
(1)请通过画找到旋转中心,将其标记为点O;
(2)直接写出旋转角α的度数.
15.如所示,P是等边三角形ABC内一点,且∠APB∶∠BPC∶∠CPA=3∶4∶5,求以PA,PB,PC为边的三角形的三个内角的度数.
16.如①,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.如②操作,固定△ABC,使△DEC绕点C按顺时针方向旋转,点D恰好落在AB边上.
(1)线段DE与AC的位置关系如何
(2)设△BDC的面积为S1,△AEC的面积为S2,则S1与S2具有怎样的数量关系
答案
1.A 2.A 3.D 4.B 5.B
6.D 7.30
8.A 90 解: 根据正方形的性质得AD=AB,∠D=∠ABF=90°,然后利用“SAS”易证得△ADE≌△ABF.又因为∠BAD=90°,所以根据旋转的定义可得△ABF可以由△ADE绕旋转中心点A按顺时针方向旋转90度得到.
9.π
10.解:如,点A的对应点为D,点C的对应点为F.△DEF是△ABC旋转后得到的三角形.
11.解:△ACD和△BCE,△FCD和△GCE,△ACF和△BCG.
理由如下:①∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,则∠BCE=∠ACD,∴△ACD≌△BCE,
∴△ACD绕点C逆时针旋转60°可得到△BCE.
②∵∠ACB=∠ECD=60°,
∴∠ACF=180°-60°-60°=60°.
又∵△ACD绕点C逆时针旋转60°可得到△BCE,
∴∠BEC=∠ADC,CE=CD.
又∵∠ACE=∠ECD,∴△FCD≌△GCE,
∴△FCD绕点C逆时针旋转60°可得到△GCE.
由①②易得△ACF绕点C逆时针旋转60°可得△BCG.
12.B 13.B
14.解:(1)如所示.
(2)如.α=∠AOA1=90°.
15.解:由题意知∠APB=90°,∠BPC=120°,∠CPA=150°.
如,把△APC绕点A顺时针旋转60°,使AC与AB重合,点P落在点P'处,连接PP',则△APP'为等边三角形,
∴PP'=PA,∠AP'P=∠APP'=60°.
∵P'B=PC,
∴△P'BP就是以PA,PB,PC为边的三角形.
∵∠BP'P=∠AP'B-∠AP'P=∠CPA-∠AP'P=150°-60°=90°,
∠BPP'=∠APB-∠APP'=90°-60°=30°,
∴∠P'BP=180°-∠BP'P-∠BPP'=60°.
故以PA,PB,PC为边的三角形的三个内角的度数分别为30°,60°,90°.
16.解:(1)由旋转可知AC=DC.
∵∠ACB=∠DCE=90°,∠B=∠CED=30°,
∴∠BAC=∠EDC=60°,∴△ADC是等边三角形,
则∠ACD=60°,∴∠ACD=∠EDC,∴DE∥AC.
(2)如,过点D作DN⊥AC于点N,过点E作EM⊥AC交AC的延长线于点M,过点C作CF⊥AB于点F,∴DN∥EM.
由(1)可知△ADC是等边三角形,DE∥AC,
∴DN=CF,四边形DNME为矩形,∴DN=EM,∴CF=EM.
∵∠ACB=90°,∠B=30°,∴AB=2AC.
又∵AD=AC,∴BD=AC.
又∵S1=CF·BD,S2=AC·EM,
∴S1=S2.
