北京课改版数学九年级下册 23.2 第2课时 旋转在坐标系、几何问题中的应用 同步课时练习(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级下册 23.2 第2课时 旋转在坐标系、几何问题中的应用 同步课时练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 249.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
第2课时 旋转在坐标系、几何问题中的应用
点P(x,y)关于原点的对称点为P'(-x,-y).
1.[2020·房山区期末] 点(-2,5)关于原点对称的点的坐标是 ( )
A.(2,5) B.(2,-5)
C.(-2,-5) D.(5,-2)
2.将点P(-2,3)向右平移3个单位长度得到点P1,点P2与P1关于原点对称,则点P2的坐标是 ( )
A.(-5,-3) B.(1,-3)
C.(-1,-3) D.(5,-3)
3.正方形ABCD在平面直角坐标系中的位置如所示,将正方形ABCD绕点A顺时针方向旋转180°后,点C的对应点C'的坐标是 ( )
A.(2,0) B.(3,0)
C.(2,-1) D.(2,1)
4.如,在平面直角坐标系xOy中,点A的坐标为(2,1),如果将线段OA绕点O逆时针方向旋转90°,那么点A的对应点的坐标为 ( )
A.(-1,2) B.(-2,1)
C.(1,-2) D.(2,-1)
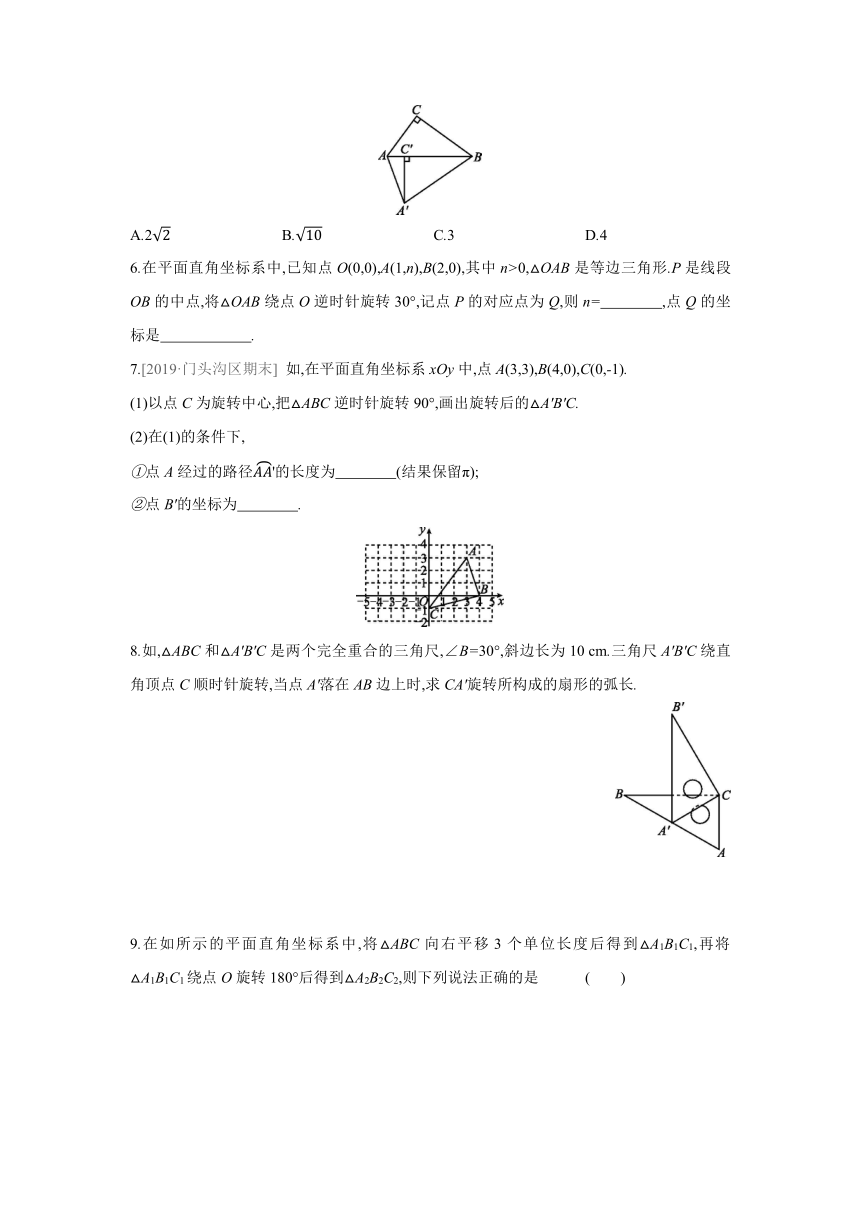
5.如,△ABC中,∠ACB=90°,AC=3.将△ABC绕点B逆时针旋转得到△A'BC',点C的对应点C'落在AB边上,A'B=5,连接AA',则AA'的长度为 ( )
A.2 B. C.3 D.4
6.在平面直角坐标系中,已知点O(0,0),A(1,n),B(2,0),其中n>0,△OAB是等边三角形.P是线段OB的中点,将△OAB绕点O逆时针旋转30°,记点P的对应点为Q,则n= ,点Q的坐标是 .
7.[2019·门头沟区期末] 如,在平面直角坐标系xOy中,点A(3,3),B(4,0),C(0,-1).
(1)以点C为旋转中心,把△ABC逆时针旋转90°,画出旋转后的△A'B'C.
(2)在(1)的条件下,
①点A经过的路径的长度为 (结果保留π);
②点B'的坐标为 .
8.如,△ABC和△A'B'C是两个完全重合的三角尺,∠B=30°,斜边长为10 cm.三角尺A'B'C绕直角顶点C顺时针旋转,当点A'落在AB边上时,求CA'旋转所构成的扇形的弧长.
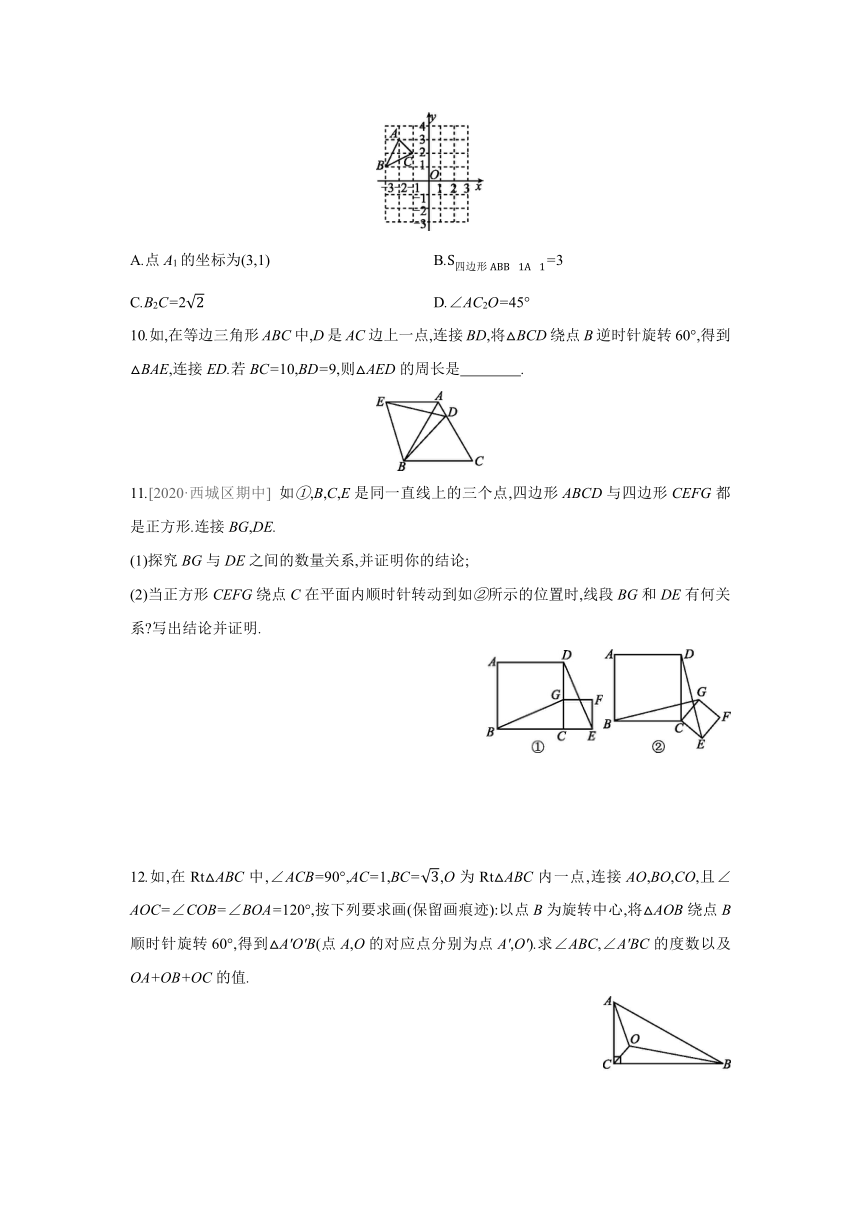
9.在如所示的平面直角坐标系中,将△ABC向右平移3个单位长度后得到△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2,则下列说法正确的是 ( )
A.点A1的坐标为(3,1) B.=3
C.B2C=2 D.∠AC2O=45°
10.如,在等边三角形ABC中,D是AC边上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是 .
11.[2020·西城区期中] 如①,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG,DE.
(1)探究BG与DE之间的数量关系,并证明你的结论;
(2)当正方形CEFG绕点C在平面内顺时针转动到如②所示的位置时,线段BG和DE有何关系 写出结论并证明.
12.如,在Rt△ABC中,∠ACB=90°,AC=1,BC=,O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画(保留画痕迹):以点B为旋转中心,将△AOB绕点B顺时针旋转60°,得到△A'O'B(点A,O的对应点分别为点A',O').求∠ABC,∠A'BC的度数以及OA+OB+OC的值.
答案
1.B 2.C
3.B 解: 由题意知AC=2,则AC'=AC=2,
所以OC'=3,故点C'的坐标是(3,0).故选B.
4.A 5.B
6. 解: 由△OAB是等边三角形,A(1,n),B(2,0),其中n>0,通过计算得n=.根据旋转中心O,旋转方向为逆时针,旋转角度为30°画,解含有30°角的直角三角形,从而得点Q的坐标为.
7.解:(1)略
(2)①π ②(-1,3)
8.解:在Rt△ABC中,由∠B=30°,AB=10 cm,得AC=AB=×10=5(cm).
根据旋转的性质知CA'=AC=5 cm.
又因为∠A=60°,
所以△AA'C是等边三角形,得∠A'CA=60°,
所以CA'旋转所构成的扇形的弧长为=(cm).
9.D 解: 如,点A1的坐标为(1,3),故A选项错误;=3×2=6,故B选项错误;B2C==,故C选项错误;变化后,点C2的坐标为(-2,-2),而A(-2,3),由可知,∠AC2O=45°,故D选项正确.
10.19 解: ∵△ABC是等边三角形,
∴AC=AB=BC=10.
∵△BAE是由△BCD绕点B逆时针旋转60°得到的,∴AE=CD,BD=BE,∠EBD=60°,
∴AE+AD=CD+AD=AC=10.
∵∠EBD=60°,BE=BD,
∴△BDE是等边三角形,∴DE=BD=9,
∴△AED的周长为AE+AD+DE=10+9=19.
11.解:(1)BG=DE.证明如下:
∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
则∠BCG=∠DCE.
∴△BCG≌△DCE,
∴BG=DE.
(2)BG=DE,且BG⊥DE.证明如下:
设BG交CD于点H,BG交DE于点P.
∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
则∠BCG=∠DCE.
∴△BCG≌△DCE,
∴BG=DE,∠CBG=∠CDE.
又∵∠CBG+∠BHC=90°,∠BHC=∠DHG,
∴∠CDE+∠DHG=90°,
∴∠DPH=90°,
即BG⊥DE.
12.解:把△AOB绕点B顺时针旋转60°得△A'O'B,如所示,
∴A'B=AB,BO'=BO,
A'O'=AO,∠AOB=∠A'O'B.
∵∠ACB=90°,AC=1,BC=,
∴tan∠ABC===,
∴∠ABC=30°,
∴∠A'BC=∠ABC+∠A'BA=30°+60°=90°.
∵∠ACB=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,∴A'B=AB=2.
∵∠OBO'=60°,BO'=BO.
连接OO',则△BOO'是等边三角形,
∴BO=OO',∠BOO'=∠BO'O=60°.
又∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO'=∠BO'A'+∠BO'O=120°+60°=180°,∴C,O,O',A'四点共线.
在Rt△A'BC中,A'C===,
∴OA+OB+OC=A'O'+OO'+OC=A'C=.
点P(x,y)关于原点的对称点为P'(-x,-y).
1.[2020·房山区期末] 点(-2,5)关于原点对称的点的坐标是 ( )
A.(2,5) B.(2,-5)
C.(-2,-5) D.(5,-2)
2.将点P(-2,3)向右平移3个单位长度得到点P1,点P2与P1关于原点对称,则点P2的坐标是 ( )
A.(-5,-3) B.(1,-3)
C.(-1,-3) D.(5,-3)
3.正方形ABCD在平面直角坐标系中的位置如所示,将正方形ABCD绕点A顺时针方向旋转180°后,点C的对应点C'的坐标是 ( )
A.(2,0) B.(3,0)
C.(2,-1) D.(2,1)
4.如,在平面直角坐标系xOy中,点A的坐标为(2,1),如果将线段OA绕点O逆时针方向旋转90°,那么点A的对应点的坐标为 ( )
A.(-1,2) B.(-2,1)
C.(1,-2) D.(2,-1)
5.如,△ABC中,∠ACB=90°,AC=3.将△ABC绕点B逆时针旋转得到△A'BC',点C的对应点C'落在AB边上,A'B=5,连接AA',则AA'的长度为 ( )
A.2 B. C.3 D.4
6.在平面直角坐标系中,已知点O(0,0),A(1,n),B(2,0),其中n>0,△OAB是等边三角形.P是线段OB的中点,将△OAB绕点O逆时针旋转30°,记点P的对应点为Q,则n= ,点Q的坐标是 .
7.[2019·门头沟区期末] 如,在平面直角坐标系xOy中,点A(3,3),B(4,0),C(0,-1).
(1)以点C为旋转中心,把△ABC逆时针旋转90°,画出旋转后的△A'B'C.
(2)在(1)的条件下,
①点A经过的路径的长度为 (结果保留π);
②点B'的坐标为 .
8.如,△ABC和△A'B'C是两个完全重合的三角尺,∠B=30°,斜边长为10 cm.三角尺A'B'C绕直角顶点C顺时针旋转,当点A'落在AB边上时,求CA'旋转所构成的扇形的弧长.
9.在如所示的平面直角坐标系中,将△ABC向右平移3个单位长度后得到△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2,则下列说法正确的是 ( )
A.点A1的坐标为(3,1) B.=3
C.B2C=2 D.∠AC2O=45°
10.如,在等边三角形ABC中,D是AC边上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是 .
11.[2020·西城区期中] 如①,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG,DE.
(1)探究BG与DE之间的数量关系,并证明你的结论;
(2)当正方形CEFG绕点C在平面内顺时针转动到如②所示的位置时,线段BG和DE有何关系 写出结论并证明.
12.如,在Rt△ABC中,∠ACB=90°,AC=1,BC=,O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画(保留画痕迹):以点B为旋转中心,将△AOB绕点B顺时针旋转60°,得到△A'O'B(点A,O的对应点分别为点A',O').求∠ABC,∠A'BC的度数以及OA+OB+OC的值.
答案
1.B 2.C
3.B 解: 由题意知AC=2,则AC'=AC=2,
所以OC'=3,故点C'的坐标是(3,0).故选B.
4.A 5.B
6. 解: 由△OAB是等边三角形,A(1,n),B(2,0),其中n>0,通过计算得n=.根据旋转中心O,旋转方向为逆时针,旋转角度为30°画,解含有30°角的直角三角形,从而得点Q的坐标为.
7.解:(1)略
(2)①π ②(-1,3)
8.解:在Rt△ABC中,由∠B=30°,AB=10 cm,得AC=AB=×10=5(cm).
根据旋转的性质知CA'=AC=5 cm.
又因为∠A=60°,
所以△AA'C是等边三角形,得∠A'CA=60°,
所以CA'旋转所构成的扇形的弧长为=(cm).
9.D 解: 如,点A1的坐标为(1,3),故A选项错误;=3×2=6,故B选项错误;B2C==,故C选项错误;变化后,点C2的坐标为(-2,-2),而A(-2,3),由可知,∠AC2O=45°,故D选项正确.
10.19 解: ∵△ABC是等边三角形,
∴AC=AB=BC=10.
∵△BAE是由△BCD绕点B逆时针旋转60°得到的,∴AE=CD,BD=BE,∠EBD=60°,
∴AE+AD=CD+AD=AC=10.
∵∠EBD=60°,BE=BD,
∴△BDE是等边三角形,∴DE=BD=9,
∴△AED的周长为AE+AD+DE=10+9=19.
11.解:(1)BG=DE.证明如下:
∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
则∠BCG=∠DCE.
∴△BCG≌△DCE,
∴BG=DE.
(2)BG=DE,且BG⊥DE.证明如下:
设BG交CD于点H,BG交DE于点P.
∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
则∠BCG=∠DCE.
∴△BCG≌△DCE,
∴BG=DE,∠CBG=∠CDE.
又∵∠CBG+∠BHC=90°,∠BHC=∠DHG,
∴∠CDE+∠DHG=90°,
∴∠DPH=90°,
即BG⊥DE.
12.解:把△AOB绕点B顺时针旋转60°得△A'O'B,如所示,
∴A'B=AB,BO'=BO,
A'O'=AO,∠AOB=∠A'O'B.
∵∠ACB=90°,AC=1,BC=,
∴tan∠ABC===,
∴∠ABC=30°,
∴∠A'BC=∠ABC+∠A'BA=30°+60°=90°.
∵∠ACB=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,∴A'B=AB=2.
∵∠OBO'=60°,BO'=BO.
连接OO',则△BOO'是等边三角形,
∴BO=OO',∠BOO'=∠BO'O=60°.
又∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO'=∠BO'A'+∠BO'O=120°+60°=180°,∴C,O,O',A'四点共线.
在Rt△A'BC中,A'C===,
∴OA+OB+OC=A'O'+OO'+OC=A'C=.
