北京课改版数学九年级下册同步课时练习:第二十四章 投影、视图与展开图 单元测试(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级下册同步课时练习:第二十四章 投影、视图与展开图 单元测试(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 236.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 17:07:31 | ||
图片预览



文档简介
第二十四章 投影、视与展开 单元测试
一、选择题(每题5分,共40分)
1.下列说法正确的是 ( )
A.物体在阳光下的投影长度只与物体的高度有关
B.小明的个子比小亮高,不论什么情况,小明的影子一定比小亮的影子长
C.物体在阳光的照射下,不同时刻,影长会发生变化,方向也会发生变化
D.物体在阳光的照射下,影子的长度和方向都是固定不变的
2.小亮在上午8时、9时30分、10时和中午12时四次到室外的阳光下观察向日葵的投影随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,则影子最长的时刻为 ( )
A.12时 B.10时
C.9时30分 D.8时
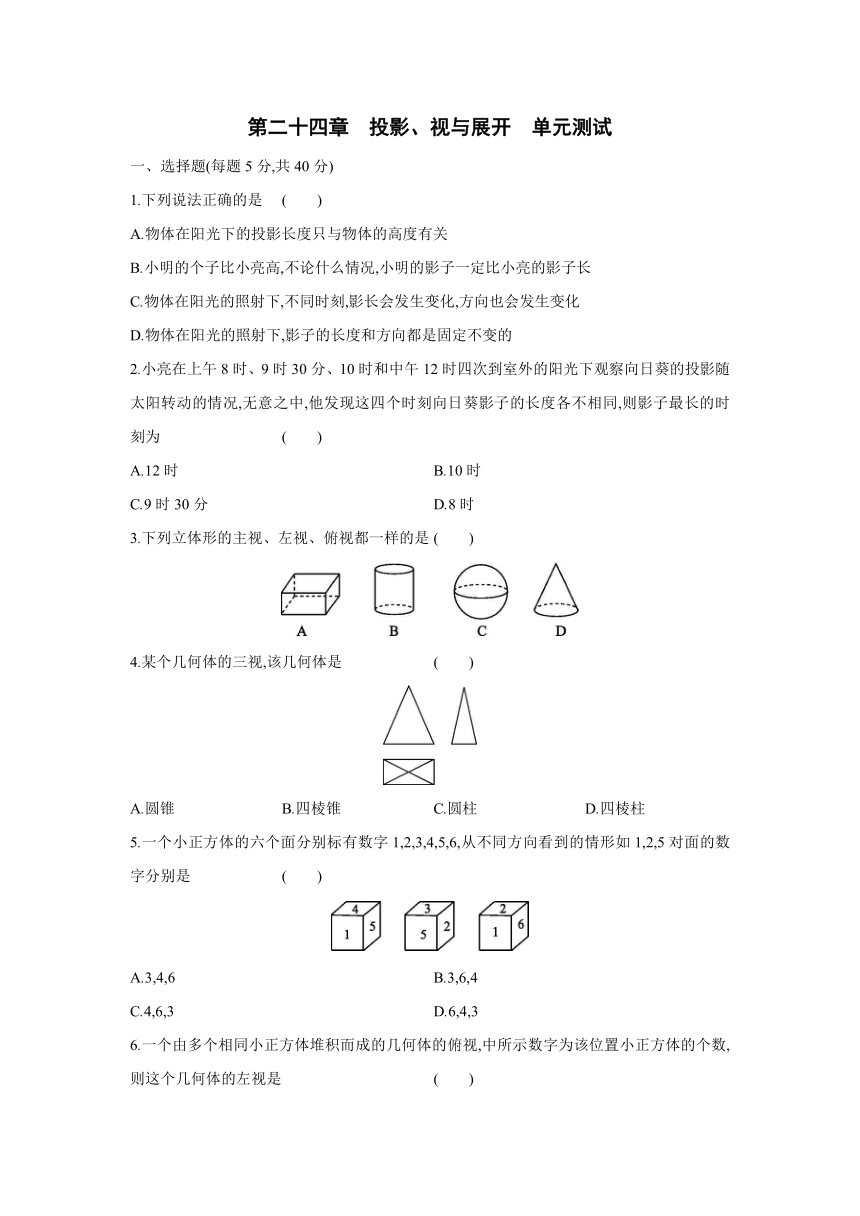
3.下列立体形的主视、左视、俯视都一样的是 ( )
4.某个几何体的三视,该几何体是 ( )
A.圆锥 B.四棱锥 C.圆柱 D.四棱柱
5.一个小正方体的六个面分别标有数字1,2,3,4,5,6,从不同方向看到的情形如1,2,5对面的数字分别是 ( )
A.3,4,6 B.3,6,4
C.4,6,3 D.6,4,3
6.一个由多个相同小正方体堆积而成的几何体的俯视,中所示数字为该位置小正方体的个数,则这个几何体的左视是 ( )
7.下列选项中,左边的平面形能够折成右边封闭的立体形的是 ( )
8.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的形如示,则这一堆方便面共有( )
A.5桶 B.6桶 C.9桶 D.12桶
二、填空题(每题5分,共15分)
9.平面直角坐标系内,一点光源位于点A(0,5)处,线段CD⊥x轴,D为垂足,C(3,1),则CD在x轴上的影长为 ,点C的影子的坐标为 .
10.如它们都是由四个大小相同的立方体以面相连接构成的不规则形状组件.其中左视与主视相同的组件是 .
11.用若干大小相同的小立方块搭成一个几何体,使得从正面和从上面看到这个几何体的形状如示,该几何体至多是用 个小立方块搭成的.
三、解答题(共45分)
12.(8分)由一些大小相同的小立方体组成的几何体的俯视如所示,其中正方形中的数字表示在该位置上的小立方体的个数,请你画出这个几何体的主视和左视.
13.(10分)由几个相同的边长为1的小立方块搭成的几何体如,格中的数字表示该位置小立方块的个数.
(1)请在下面方格纸中分别画出这个几何体的主视和左视;
(2)根据三视,这个几何体的表面积为 ;(包括底面积)
(3)若上述小立方块搭成的几何体的俯视不变,在小立方块总数不变,位置可以改变的前提下,则搭成的不同的几何体中,表面积最大的为 .(包括底面积)
14.(12分)是某几何体的三视.
(1)写出这个几何体的名称;
(2)画出它的一种平面展开;
(3)根据中的数据(单位:cm),求这个几何体的所有棱长的和与它的体积.
15.(15分)综合与实践:制作无盖盒子.
任务一:如,有一块矩形纸板,长是宽的2倍,要将其四个角各剪去一个正方形,折成高为4 cm,容积为616 cm3的无盖长方体盒子(纸板厚度及剪切接缝处损耗忽略不计).
(1)请在①的矩形纸板中画出示意,用实线表示剪切线,虚线表示折痕;
(2)请求出这块矩形纸板的长和宽.
任务二:①是一个高为4 cm的无盖的五棱柱盒子(直棱柱),②是其底面,在五边形ABCDE中,BC=12 cm,AB=DC=6 cm,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°.
(1)试判断②中AE与DE的数量关系,并加以证明;
(2)①中的五棱柱盒子可按③所示的示意,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少为多少厘米 请直接写出结果.(中实线表示剪切线,虚线表示折痕,纸板厚度及剪切接缝处损耗忽略不计)
答案
1.C 2.D 3.C 4.B 5.A 6.B
7.B 8.A 9.
10.(1)(2)(4) 解: (1)左视为,主视为,左视与主视相同,故此项符合题意;
(2)左视为,主视为,左视与主视相同,故此项符合题意;
(3)左视为,主视为,左视与主视不同,故此项不符合题意;
(4)左视为,主视为,左视与主视相同,故此项符合题意.
故答案为(1)(2)(4).
11.8 解: 由俯视可知该几何体底层有5个小立方块,由主视可知上层左侧至多有3个小立方块,∴该几何体至多是用8个小立方块搭成的.
12.解:如所示.
13.解:(1)如所示.
(2)这个几何体的表面积为2×(5+4+3)=24.
(3)要使表面积最大,则需满足两立方块重合的最少,此时俯视如下:
故表面积为1×(3+3+5+5+5+5)=26.
14.解: (1)三视的主视是一个矩形,而左视是一个正方形,俯视为一个三角形,故可知这是一个三棱柱;
(2)易得展开为三个长方形加两个三角形,注意各边之间的长短关系;
(3)根据直三棱柱的特点及其体积公式计算即可.
解:(1)这个几何体为三棱柱.
(2)它的平面展开如所示(答案不唯一).
(3)这个几何体的所有棱长之和为(3+4+5)×2+4×3=36(cm).
因为俯视各边长分别为3 cm,4 cm,5 cm,且32+42=52,所以俯视为直角三角形,所以它的体积为×3×4×4=24(cm3).
15.解:任务一:(1)按要求画出示意(如).
(2)设矩形纸板的宽为x cm,则长为2x cm.由题意,得4(x-2×4)(2x-2×4)=616,
解得x1=15,x2=-3(不合题意,舍去),
则2x=2×15=30.
答:这块矩形纸板的长为30 cm,宽为15 cm.
任务二:(1)AE=DE.证明如下:
如,延长EA,ED,分别交直线BC于点M,N.
∵∠ABC=∠BCD=120°,
∴∠ABM=∠DCN=60°.
又∵∠EAB=∠EDC=90°,
∴∠M=∠N=90°-60°=30°,
∴EM=EN.
在△MAB和△NDC中,
∴△MAB≌△NDC(AAS),
∴AM=DN,
∴EM-AM=EN-DN,
即AE=DE.
(2)长至少为(18+4)cm,宽至少为(4+8)cm.
一、选择题(每题5分,共40分)
1.下列说法正确的是 ( )
A.物体在阳光下的投影长度只与物体的高度有关
B.小明的个子比小亮高,不论什么情况,小明的影子一定比小亮的影子长
C.物体在阳光的照射下,不同时刻,影长会发生变化,方向也会发生变化
D.物体在阳光的照射下,影子的长度和方向都是固定不变的
2.小亮在上午8时、9时30分、10时和中午12时四次到室外的阳光下观察向日葵的投影随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,则影子最长的时刻为 ( )
A.12时 B.10时
C.9时30分 D.8时
3.下列立体形的主视、左视、俯视都一样的是 ( )
4.某个几何体的三视,该几何体是 ( )
A.圆锥 B.四棱锥 C.圆柱 D.四棱柱
5.一个小正方体的六个面分别标有数字1,2,3,4,5,6,从不同方向看到的情形如1,2,5对面的数字分别是 ( )
A.3,4,6 B.3,6,4
C.4,6,3 D.6,4,3
6.一个由多个相同小正方体堆积而成的几何体的俯视,中所示数字为该位置小正方体的个数,则这个几何体的左视是 ( )
7.下列选项中,左边的平面形能够折成右边封闭的立体形的是 ( )
8.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的形如示,则这一堆方便面共有( )
A.5桶 B.6桶 C.9桶 D.12桶
二、填空题(每题5分,共15分)
9.平面直角坐标系内,一点光源位于点A(0,5)处,线段CD⊥x轴,D为垂足,C(3,1),则CD在x轴上的影长为 ,点C的影子的坐标为 .
10.如它们都是由四个大小相同的立方体以面相连接构成的不规则形状组件.其中左视与主视相同的组件是 .
11.用若干大小相同的小立方块搭成一个几何体,使得从正面和从上面看到这个几何体的形状如示,该几何体至多是用 个小立方块搭成的.
三、解答题(共45分)
12.(8分)由一些大小相同的小立方体组成的几何体的俯视如所示,其中正方形中的数字表示在该位置上的小立方体的个数,请你画出这个几何体的主视和左视.
13.(10分)由几个相同的边长为1的小立方块搭成的几何体如,格中的数字表示该位置小立方块的个数.
(1)请在下面方格纸中分别画出这个几何体的主视和左视;
(2)根据三视,这个几何体的表面积为 ;(包括底面积)
(3)若上述小立方块搭成的几何体的俯视不变,在小立方块总数不变,位置可以改变的前提下,则搭成的不同的几何体中,表面积最大的为 .(包括底面积)
14.(12分)是某几何体的三视.
(1)写出这个几何体的名称;
(2)画出它的一种平面展开;
(3)根据中的数据(单位:cm),求这个几何体的所有棱长的和与它的体积.
15.(15分)综合与实践:制作无盖盒子.
任务一:如,有一块矩形纸板,长是宽的2倍,要将其四个角各剪去一个正方形,折成高为4 cm,容积为616 cm3的无盖长方体盒子(纸板厚度及剪切接缝处损耗忽略不计).
(1)请在①的矩形纸板中画出示意,用实线表示剪切线,虚线表示折痕;
(2)请求出这块矩形纸板的长和宽.
任务二:①是一个高为4 cm的无盖的五棱柱盒子(直棱柱),②是其底面,在五边形ABCDE中,BC=12 cm,AB=DC=6 cm,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°.
(1)试判断②中AE与DE的数量关系,并加以证明;
(2)①中的五棱柱盒子可按③所示的示意,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少为多少厘米 请直接写出结果.(中实线表示剪切线,虚线表示折痕,纸板厚度及剪切接缝处损耗忽略不计)
答案
1.C 2.D 3.C 4.B 5.A 6.B
7.B 8.A 9.
10.(1)(2)(4) 解: (1)左视为,主视为,左视与主视相同,故此项符合题意;
(2)左视为,主视为,左视与主视相同,故此项符合题意;
(3)左视为,主视为,左视与主视不同,故此项不符合题意;
(4)左视为,主视为,左视与主视相同,故此项符合题意.
故答案为(1)(2)(4).
11.8 解: 由俯视可知该几何体底层有5个小立方块,由主视可知上层左侧至多有3个小立方块,∴该几何体至多是用8个小立方块搭成的.
12.解:如所示.
13.解:(1)如所示.
(2)这个几何体的表面积为2×(5+4+3)=24.
(3)要使表面积最大,则需满足两立方块重合的最少,此时俯视如下:
故表面积为1×(3+3+5+5+5+5)=26.
14.解: (1)三视的主视是一个矩形,而左视是一个正方形,俯视为一个三角形,故可知这是一个三棱柱;
(2)易得展开为三个长方形加两个三角形,注意各边之间的长短关系;
(3)根据直三棱柱的特点及其体积公式计算即可.
解:(1)这个几何体为三棱柱.
(2)它的平面展开如所示(答案不唯一).
(3)这个几何体的所有棱长之和为(3+4+5)×2+4×3=36(cm).
因为俯视各边长分别为3 cm,4 cm,5 cm,且32+42=52,所以俯视为直角三角形,所以它的体积为×3×4×4=24(cm3).
15.解:任务一:(1)按要求画出示意(如).
(2)设矩形纸板的宽为x cm,则长为2x cm.由题意,得4(x-2×4)(2x-2×4)=616,
解得x1=15,x2=-3(不合题意,舍去),
则2x=2×15=30.
答:这块矩形纸板的长为30 cm,宽为15 cm.
任务二:(1)AE=DE.证明如下:
如,延长EA,ED,分别交直线BC于点M,N.
∵∠ABC=∠BCD=120°,
∴∠ABM=∠DCN=60°.
又∵∠EAB=∠EDC=90°,
∴∠M=∠N=90°-60°=30°,
∴EM=EN.
在△MAB和△NDC中,
∴△MAB≌△NDC(AAS),
∴AM=DN,
∴EM-AM=EN-DN,
即AE=DE.
(2)长至少为(18+4)cm,宽至少为(4+8)cm.
