北京课改版数学九年级下册同步课时练习:第二十四章 投影、视图与展开图 单元复习(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级下册同步课时练习:第二十四章 投影、视图与展开图 单元复习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 366.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
回顾与整理
类型一 平行投影
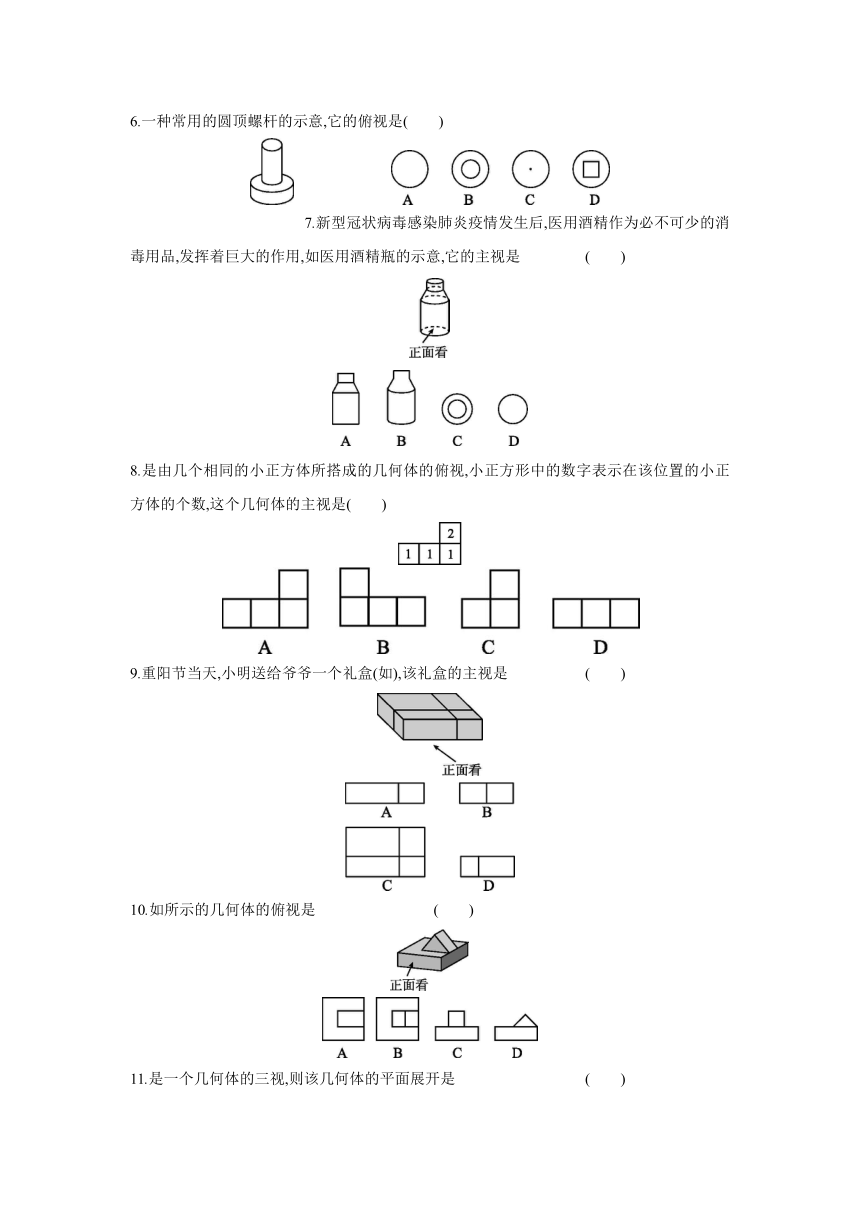
1.[2020·丰台区期末] 在测量旗杆高度的活动课中,某小组学生于同一时刻在阳光下对一根直立于平地的竹竿及其影长和旗杆的影长进行了测量,得到的数据如示,根据这些数据计算出旗杆的高度为 m.
类型二 中心投影
2.如小树AB在路灯O的照射下形成树影BC.若树高AB=2 m,树影BC=3 m,树与路灯的水平距离BP=4 m,则路灯的高度OP为 m.
3.如示,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿AO所在的直线行走14米到点B时,人影的长度 ( )
A.增大了1.5米 B.减小了1.5米
C.增大了3.5米 D.减小了3.5米
类型三 确定简单几何体的三视
4.[2020·石景山区一模] 在下列几何体中,其三视中没有矩形的是 ( )
5.如示的简单几何体的左视是 ( )
6.一种常用的圆顶螺杆的示意,它的俯视是( )
7.新型冠状病毒感染肺炎疫情发生后,医用酒精作为必不可少的消毒用品,发挥着巨大的作用,如医用酒精瓶的示意,它的主视是 ( )
8.是由几个相同的小正方体所搭成的几何体的俯视,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视是( )
9.重阳节当天,小明送给爷爷一个礼盒(如),该礼盒的主视是 ( )
10.如所示的几何体的俯视是 ( )
11.是一个几何体的三视,则该几何体的平面展开是 ( )
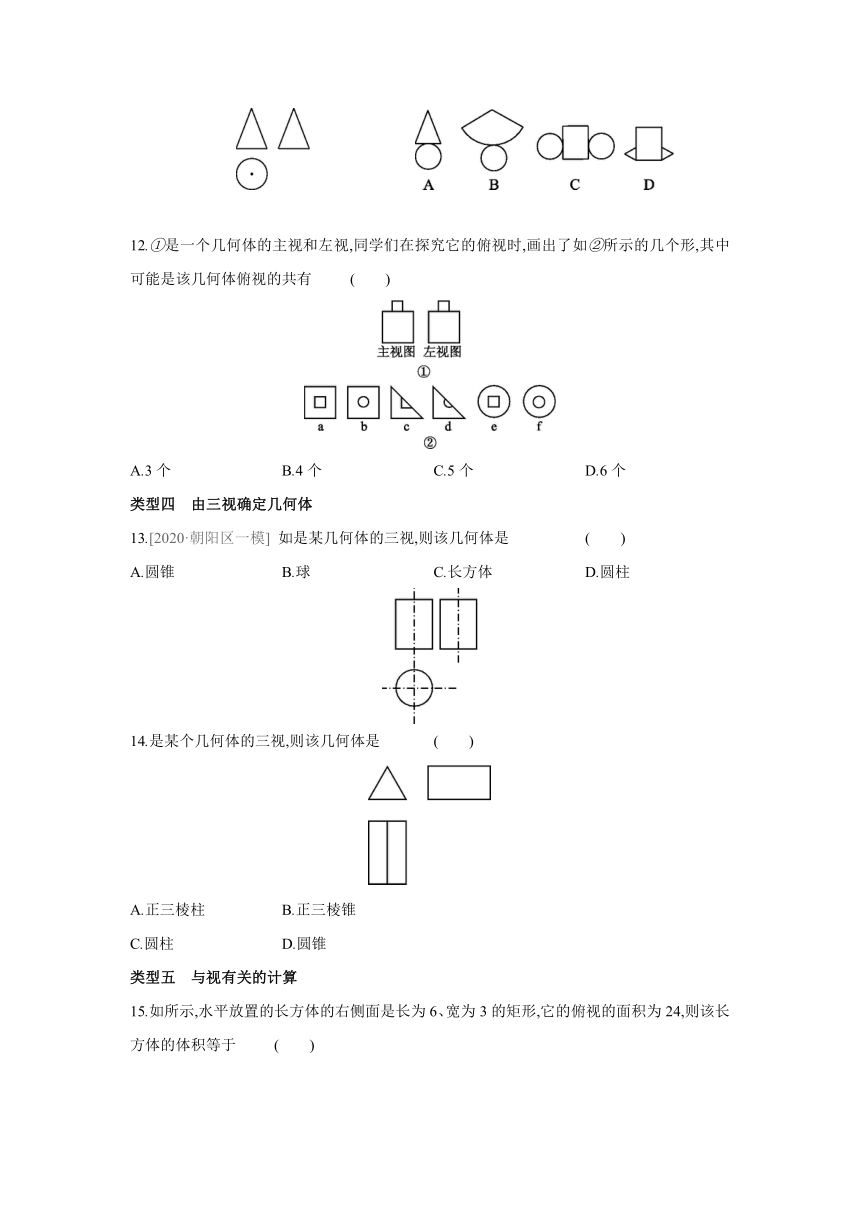
12.①是一个几何体的主视和左视,同学们在探究它的俯视时,画出了如②所示的几个形,其中可能是该几何体俯视的共有 ( )
A.3个 B.4个 C.5个 D.6个
类型四 由三视确定几何体
13.[2020·朝阳区一模] 如是某几何体的三视,则该几何体是 ( )
A.圆锥 B.球 C.长方体 D.圆柱
14.是某个几何体的三视,则该几何体是 ( )
A.正三棱柱 B.正三棱锥
C.圆柱 D.圆锥
类型五 与视有关的计算
15.如所示,水平放置的长方体的右侧面是长为6、宽为3的矩形,它的俯视的面积为24,则该长方体的体积等于 ( )
A.32 B.48 C.72 D.144
16.将棱长是1 cm的小正方体组成如所示的几何体,那么这个几何体的表面积是
cm2.
类型六 基本几何体的平面展开
17.某校九年级(1)班在“迎中考百日誓师”活动中打算制作一个带有正方体挂坠的倒计时牌挂在班级,正方体的每个面上分别书写“成功舍我其谁”六个字中的一个.是该班同学设计的正方体挂坠的平面展开,那么“我”字对面的字是 ( )
A.舍 B.功 C.其 D.谁
18.[2020·门头沟区期末] 如是一个正方体纸盒,下面四个平面形中,是这个正方体纸盒展开的是 ( )
19.如,一个几何体上半部分为正四棱锥,下半部分为正方体,且有一个面涂有颜色.中是该几何体的平面展开的是( )
20.如,②是①的表面展开,②已有两个面标出是长方体的下面和右面,请你在②中把长方体的其他面标出来.
答案
1.12 2.
3.D 解: 小明在两个不同的位置时,均可构成两个相似三角形,可利用相似比求人影长度的变化.
设小明在A处时影长为x米,在B处时影长为y米,则=,∴x=5.
=,∴y=1.5.
∵x-y=3.5,∴人影的长度减小了3.5米.故选D.
4.C 5.A 6.B 7.A 8.A
9.A 解: 从正面看,是两个矩形,右边的较小.故选A.
10.B 11.B 12.C 13.D 14.A
15.D 解: 由俯视的面积=长×宽=24,可知长方体的体积=长×宽×高=24×6=144.故选D.
16.36 解: 本题直接求表面积有点复杂,采用视法比较简单.根据物体可确定这个几何体的三种视,三种视的面积相等,都是6 cm2,所以这个几何体的表面积是6×6=36(cm2).
17.D 18.C 19.B
20.解:(自上而下至左)后面,上面,前面,左面或前面,上面,后面,左面.
类型一 平行投影
1.[2020·丰台区期末] 在测量旗杆高度的活动课中,某小组学生于同一时刻在阳光下对一根直立于平地的竹竿及其影长和旗杆的影长进行了测量,得到的数据如示,根据这些数据计算出旗杆的高度为 m.
类型二 中心投影
2.如小树AB在路灯O的照射下形成树影BC.若树高AB=2 m,树影BC=3 m,树与路灯的水平距离BP=4 m,则路灯的高度OP为 m.
3.如示,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿AO所在的直线行走14米到点B时,人影的长度 ( )
A.增大了1.5米 B.减小了1.5米
C.增大了3.5米 D.减小了3.5米
类型三 确定简单几何体的三视
4.[2020·石景山区一模] 在下列几何体中,其三视中没有矩形的是 ( )
5.如示的简单几何体的左视是 ( )
6.一种常用的圆顶螺杆的示意,它的俯视是( )
7.新型冠状病毒感染肺炎疫情发生后,医用酒精作为必不可少的消毒用品,发挥着巨大的作用,如医用酒精瓶的示意,它的主视是 ( )
8.是由几个相同的小正方体所搭成的几何体的俯视,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视是( )
9.重阳节当天,小明送给爷爷一个礼盒(如),该礼盒的主视是 ( )
10.如所示的几何体的俯视是 ( )
11.是一个几何体的三视,则该几何体的平面展开是 ( )
12.①是一个几何体的主视和左视,同学们在探究它的俯视时,画出了如②所示的几个形,其中可能是该几何体俯视的共有 ( )
A.3个 B.4个 C.5个 D.6个
类型四 由三视确定几何体
13.[2020·朝阳区一模] 如是某几何体的三视,则该几何体是 ( )
A.圆锥 B.球 C.长方体 D.圆柱
14.是某个几何体的三视,则该几何体是 ( )
A.正三棱柱 B.正三棱锥
C.圆柱 D.圆锥
类型五 与视有关的计算
15.如所示,水平放置的长方体的右侧面是长为6、宽为3的矩形,它的俯视的面积为24,则该长方体的体积等于 ( )
A.32 B.48 C.72 D.144
16.将棱长是1 cm的小正方体组成如所示的几何体,那么这个几何体的表面积是
cm2.
类型六 基本几何体的平面展开
17.某校九年级(1)班在“迎中考百日誓师”活动中打算制作一个带有正方体挂坠的倒计时牌挂在班级,正方体的每个面上分别书写“成功舍我其谁”六个字中的一个.是该班同学设计的正方体挂坠的平面展开,那么“我”字对面的字是 ( )
A.舍 B.功 C.其 D.谁
18.[2020·门头沟区期末] 如是一个正方体纸盒,下面四个平面形中,是这个正方体纸盒展开的是 ( )
19.如,一个几何体上半部分为正四棱锥,下半部分为正方体,且有一个面涂有颜色.中是该几何体的平面展开的是( )
20.如,②是①的表面展开,②已有两个面标出是长方体的下面和右面,请你在②中把长方体的其他面标出来.
答案
1.12 2.
3.D 解: 小明在两个不同的位置时,均可构成两个相似三角形,可利用相似比求人影长度的变化.
设小明在A处时影长为x米,在B处时影长为y米,则=,∴x=5.
=,∴y=1.5.
∵x-y=3.5,∴人影的长度减小了3.5米.故选D.
4.C 5.A 6.B 7.A 8.A
9.A 解: 从正面看,是两个矩形,右边的较小.故选A.
10.B 11.B 12.C 13.D 14.A
15.D 解: 由俯视的面积=长×宽=24,可知长方体的体积=长×宽×高=24×6=144.故选D.
16.36 解: 本题直接求表面积有点复杂,采用视法比较简单.根据物体可确定这个几何体的三种视,三种视的面积相等,都是6 cm2,所以这个几何体的表面积是6×6=36(cm2).
17.D 18.C 19.B
20.解:(自上而下至左)后面,上面,前面,左面或前面,上面,后面,左面.
