沪科版九年级数学下册24.2《《圆的对称性》教案》教学设计
文档属性
| 名称 | 沪科版九年级数学下册24.2《《圆的对称性》教案》教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 84.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
《圆的对称性》教案
教学目标
1.知识与技能
(1)理解圆的轴对称性和中心对称性,会画出圆的对称轴,会找圆的对称中心;
(2)掌握圆心角、弧和弦之间的关系,并会用它们之间的关系解题.
2.过程与方法
(1)通过对圆的对称性的理解,培养学生的观察、分析、发现问题和概括问题的能力,促进学生创造性思维水平的发展和提高;
(2)通过对圆心角、弧和弦之间的关系的探究,掌握解题的方法和技巧.
3.情感、态度与价值观
经过观察、总结和应用等数学活动,感受数学活动充满了探索性与创造性,体验发现的乐趣.
教学重难点
重点:对圆心角、弧和弦之间的关系的理解.
难点:能灵活运用圆的对称性解决有关实际问题,会用圆心角、弧和弦之间的关系解题.
教学过程
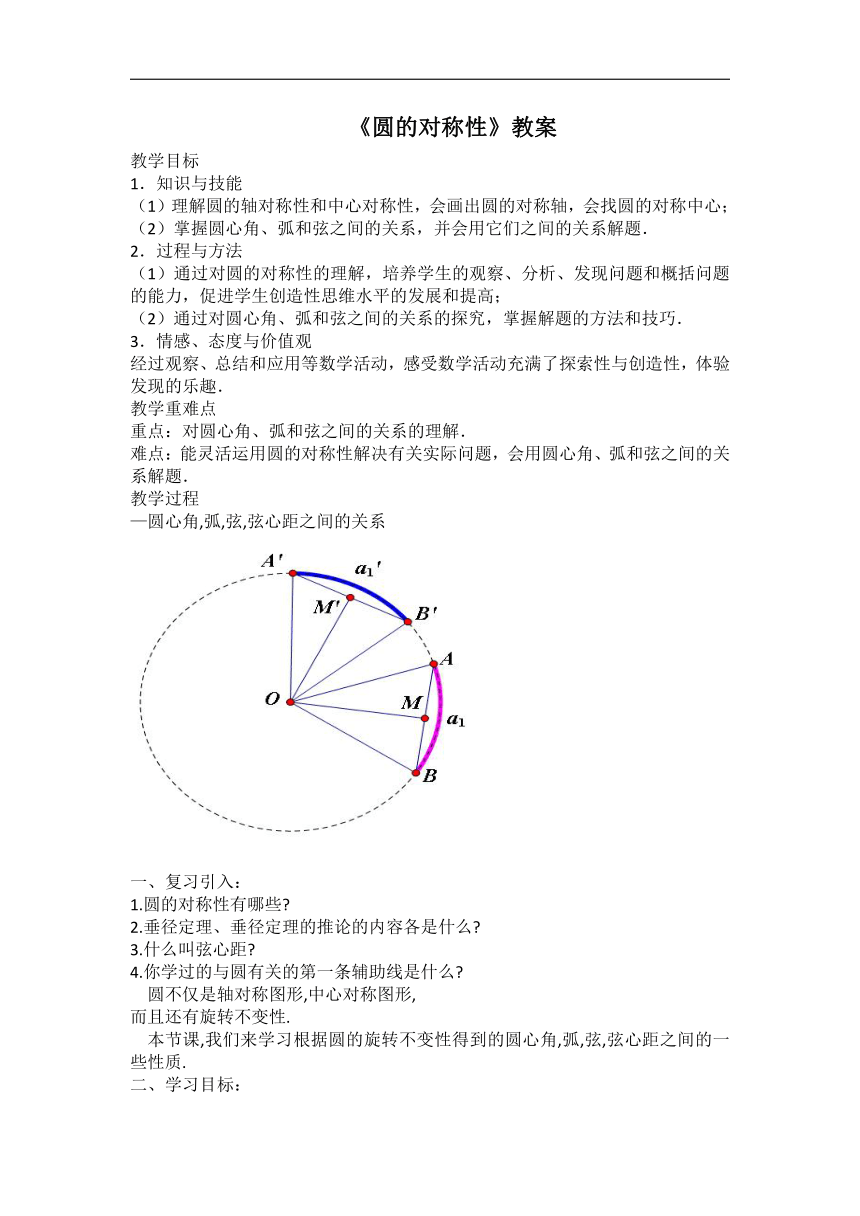
—圆心角,弧,弦,弦心距之间的关系
一、复习引入:
1.圆的对称性有哪些
2.垂径定理、垂径定理的推论的内容各是什么
3.什么叫弦心距
4.你学过的与圆有关的第一条辅助线是什么
圆不仅是轴对称图形,中心对称图形,
而且还有旋转不变性.
本节课,我们来学习根据圆的旋转不变性得到的圆心角,弧,弦,弦心距之间的一些性质.
二、学习目标:
1、掌握圆心角定义,理解并掌握圆心角,弧,弦,弦心距之间的关系
2、理解并掌握圆心角的度数与它所对的弧的度数
之间的关系。
能利用圆心角、弧、弦、弦心距之间的关系解决有关的证明与计算问题。
三、自学提纲:
看书本上第18-19页内容,解决以下问题:
1.什么叫圆心角?
2.圆心角,弧,弦,弦心距之间的相等关系定理及其推论的内容是什么?怎样用符号语言来表述?
3.圆心角的度数等于它所对弧的度数吗?
4.阅读书本上例4、5、6.掌握解题方法与解题步骤
四、合作探究
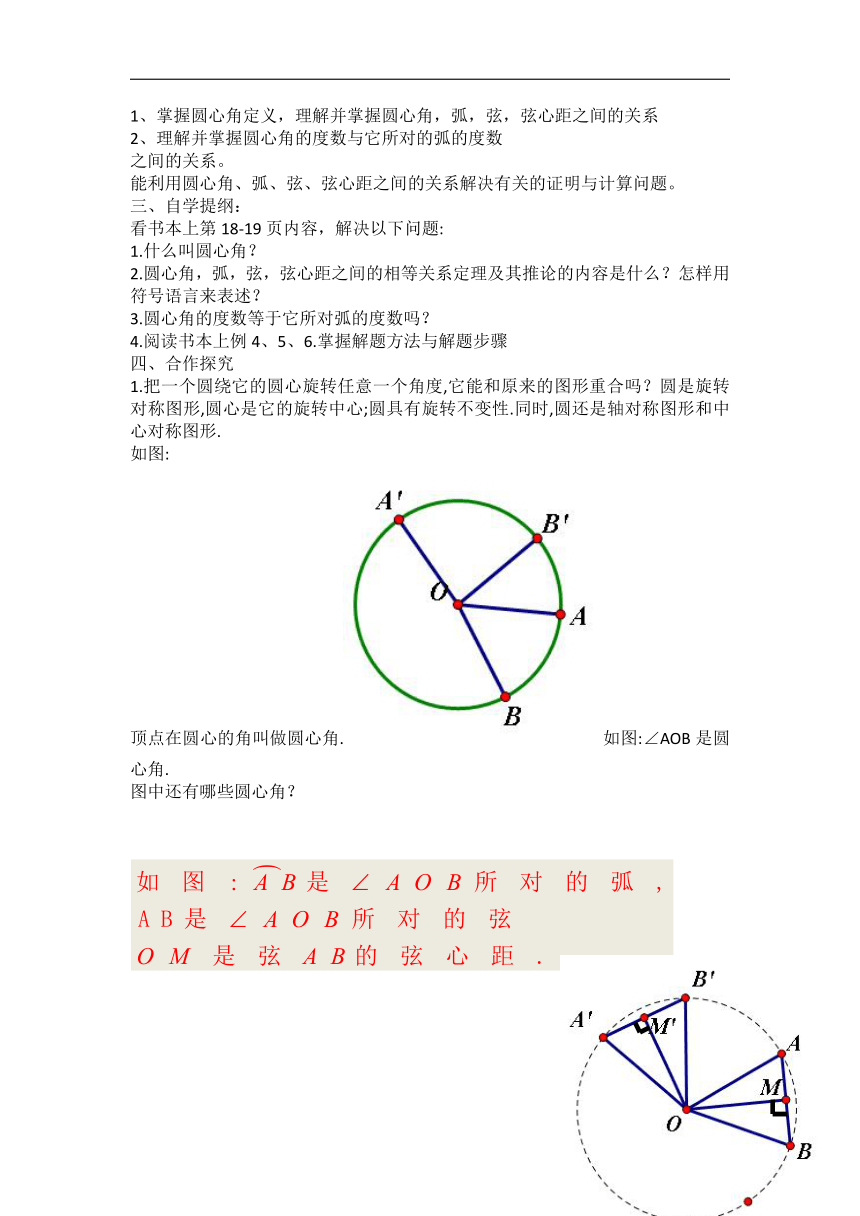
1.把一个圆绕它的圆心旋转任意一个角度,它能和原来的图形重合吗?圆是旋转对称图形,圆心是它的旋转中心;圆具有旋转不变性.同时,圆还是轴对称图形和中心对称图形.
如图:
顶点在圆心的角叫做圆心角.如图:∠AOB是圆心角.
图中还有哪些圆心角?
2.演示:圆心角,弧,弦,弦心距之间的关系有:
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距
相等。
3.推论:
在同圆或等圆中,如果两个圆心角,以及这两个角所对的弧,所对的弦,所对的弦的弦心距中,
有一组量相等,那么其余各组量都分别相等.
4.把顶点在圆心的周角等分成360份,每一份的圆心角是1°的角.因为同圆中相等的圆心角所对的弧相等,所以整个圆周也被等分成360份,我们把每一份这样的弧叫做1°的弧.一般地:n0的圆心角对着n0的弧,n0的弧对着n0的圆心角.
例4已知:等边三角形ABC的三个顶点都在⊙O上,求证:∠AOB=∠BOC=∠AOC=120°
例5.已知:点O是∠PAQ平分线上的一点,⊙O分别交∠A两边于点C,D和点E,F。
求证:CD=EF
变式题:
已知:⊙O分别交∠PAQ的两边于C,D,E,F,且CD=EF。
求证:AO平分∠PAQ。
五、巩固新知,当堂训练
已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么______。
(2)如果OE=OF,那么_______。
(3)如果AB=CD 那么 .
(4)如果∠AOB=∠COD那么____。
六、课堂小结
本节课你学了哪些内容,有什么收获?
七、作业布置:
课堂作业:
必做题:书本上第21页第8题
选做题:书本上第21页第9题
课外作业:基础训练同步
教学目标
1.知识与技能
(1)理解圆的轴对称性和中心对称性,会画出圆的对称轴,会找圆的对称中心;
(2)掌握圆心角、弧和弦之间的关系,并会用它们之间的关系解题.
2.过程与方法
(1)通过对圆的对称性的理解,培养学生的观察、分析、发现问题和概括问题的能力,促进学生创造性思维水平的发展和提高;
(2)通过对圆心角、弧和弦之间的关系的探究,掌握解题的方法和技巧.
3.情感、态度与价值观
经过观察、总结和应用等数学活动,感受数学活动充满了探索性与创造性,体验发现的乐趣.
教学重难点
重点:对圆心角、弧和弦之间的关系的理解.
难点:能灵活运用圆的对称性解决有关实际问题,会用圆心角、弧和弦之间的关系解题.
教学过程
—圆心角,弧,弦,弦心距之间的关系
一、复习引入:
1.圆的对称性有哪些
2.垂径定理、垂径定理的推论的内容各是什么
3.什么叫弦心距
4.你学过的与圆有关的第一条辅助线是什么
圆不仅是轴对称图形,中心对称图形,
而且还有旋转不变性.
本节课,我们来学习根据圆的旋转不变性得到的圆心角,弧,弦,弦心距之间的一些性质.
二、学习目标:
1、掌握圆心角定义,理解并掌握圆心角,弧,弦,弦心距之间的关系
2、理解并掌握圆心角的度数与它所对的弧的度数
之间的关系。
能利用圆心角、弧、弦、弦心距之间的关系解决有关的证明与计算问题。
三、自学提纲:
看书本上第18-19页内容,解决以下问题:
1.什么叫圆心角?
2.圆心角,弧,弦,弦心距之间的相等关系定理及其推论的内容是什么?怎样用符号语言来表述?
3.圆心角的度数等于它所对弧的度数吗?
4.阅读书本上例4、5、6.掌握解题方法与解题步骤
四、合作探究
1.把一个圆绕它的圆心旋转任意一个角度,它能和原来的图形重合吗?圆是旋转对称图形,圆心是它的旋转中心;圆具有旋转不变性.同时,圆还是轴对称图形和中心对称图形.
如图:
顶点在圆心的角叫做圆心角.如图:∠AOB是圆心角.
图中还有哪些圆心角?
2.演示:圆心角,弧,弦,弦心距之间的关系有:
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距
相等。
3.推论:
在同圆或等圆中,如果两个圆心角,以及这两个角所对的弧,所对的弦,所对的弦的弦心距中,
有一组量相等,那么其余各组量都分别相等.
4.把顶点在圆心的周角等分成360份,每一份的圆心角是1°的角.因为同圆中相等的圆心角所对的弧相等,所以整个圆周也被等分成360份,我们把每一份这样的弧叫做1°的弧.一般地:n0的圆心角对着n0的弧,n0的弧对着n0的圆心角.
例4已知:等边三角形ABC的三个顶点都在⊙O上,求证:∠AOB=∠BOC=∠AOC=120°
例5.已知:点O是∠PAQ平分线上的一点,⊙O分别交∠A两边于点C,D和点E,F。
求证:CD=EF
变式题:
已知:⊙O分别交∠PAQ的两边于C,D,E,F,且CD=EF。
求证:AO平分∠PAQ。
五、巩固新知,当堂训练
已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么______。
(2)如果OE=OF,那么_______。
(3)如果AB=CD 那么 .
(4)如果∠AOB=∠COD那么____。
六、课堂小结
本节课你学了哪些内容,有什么收获?
七、作业布置:
课堂作业:
必做题:书本上第21页第8题
选做题:书本上第21页第9题
课外作业:基础训练同步
