沪科版九年级数学下册 26.2 等可能情形下的概率计算 教案
文档属性
| 名称 | 沪科版九年级数学下册 26.2 等可能情形下的概率计算 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
26.2 等可能情形下的概率计算
第1课时
学习目标:
1、在解决实际问题的过程中,体会随机的思想,
进一步理解概率的意义。
2、理解等可能情形下的随机事件的概率,会运用
列举法计算随机事件的概率。
重点:等可能情形下的所有可能结果的确定
难点:掌握等可能情形下的随机事件的概率的意义
教学方法:三段六步教学法
学习方法:小组化学习
教学准备:班班通畅言系统资源、自制课件、导学案、同步练习
教学过程
一、复习引入:
1.必然事件、不可能事件、随机事件、概率的概念?
2、口答:
(1)投掷一枚均匀的硬币1次,则P(正面朝上)=____;
(2)袋中有6个除颜色外完全相同的小球,其中2个白球,2个黑球,1个红球,1个黄球,从中任意摸出1个球,则 P(白球)=_____ ;P(黑球)=_____;
P(红球)=______;P(黄球)=_______.
二、展示课题与学习目标:
1、在解决实际问题的过程中,体会随机的思想,
进一步理解概率的意义。
2、理解等可能情形下的随机事件的概率,会运用
列举法计算随机事件的概率。
三、自学提纲:
看书95-97页,解决以下问题:
1、计算概率的公式是什么?
2、一个随机事件发生的概率P(A)的范围是什么
必然事件、不可能事件的概率分别是多少
3、树状图有什么特点?
4、自学例1、例2、例3.
自学指导:先独立完成学习任务,再组内交流讨论,汇报收获和疑惑
说一说:
1.从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,有几种可能性,每种的可能性各是多少呢
2.掷一个骰子,向上一面的点数共有几种可能,每种的可能性各是多少?
1,2,3,4,5
1,2,3,4,5,6
教师展示实验,学生思考、交流作答,教师根据情况点评归纳
上面的问题中,都有两个共同的特点:
1)在一次实验中,可能出现的不同结果都只有有限多个.
2) 在一次实验中,各种结果发生的可能性相等.
一般地,如果在一次实验中,有n种可能的结果,并且它们发生的可能性相等,其中使事件A发生的结果数有m( m≤n )种,那么事件A发生的概率为:
当A是必然事件时,m=n, P(A)=1;
当A是不可能事件时,m=0, P(A)=0.
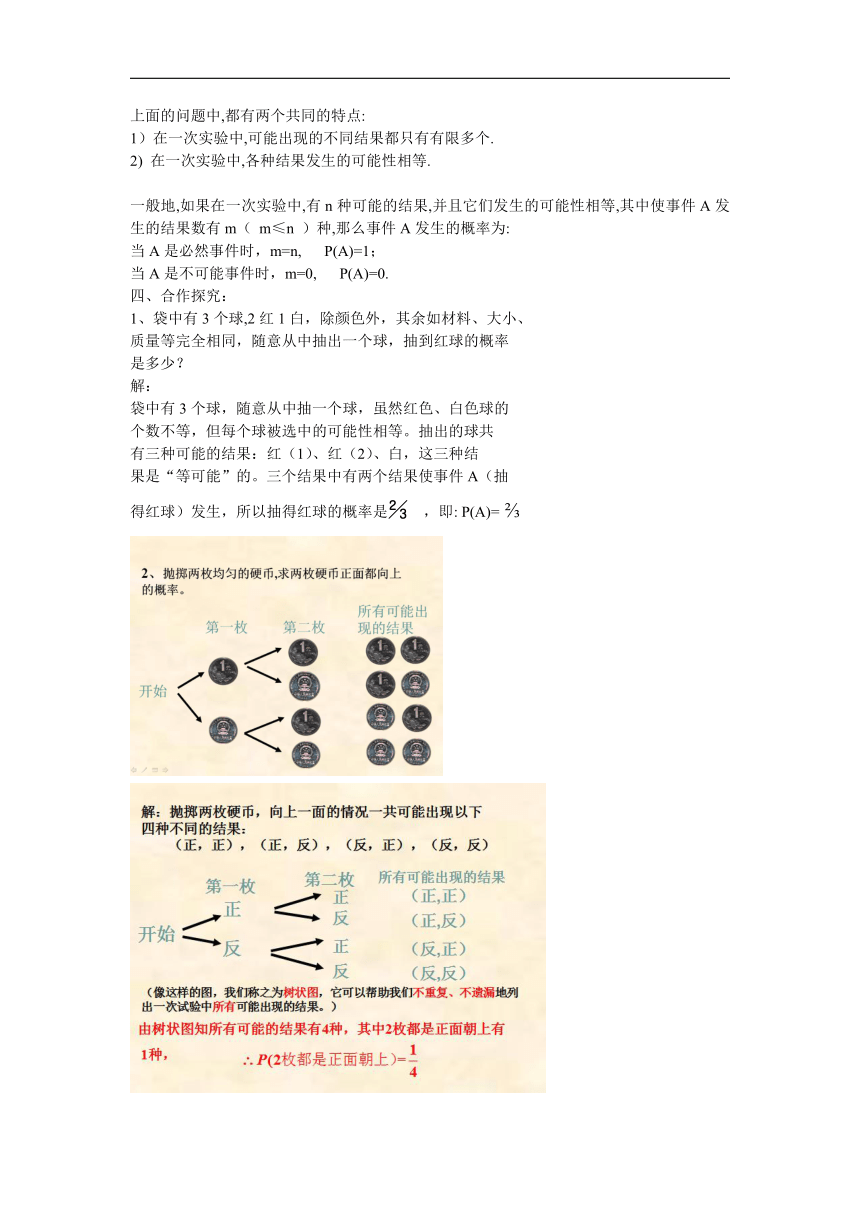
四、合作探究:
1、袋中有3个球,2红1白,除颜色外,其余如材料、大小、
质量等完全相同,随意从中抽出一个球,抽到红球的概率
是多少?
解:
袋中有3个球,随意从中抽一个球,虽然红色、白色球的
个数不等,但每个球被选中的可能性相等。抽出的球共
有三种可能的结果:红(1)、红(2)、白,这三种结
果是“等可能”的。三个结果中有两个结果使事件A(抽
得红球)发生,所以抽得红球的概率是 ,即: P(A)=
(像这样的图,我们称之为树状图,它可以帮助我们不重复、不遗漏地列出一次试验中所有可能出现的结果。)
由树状图知所有可能的结果有4种,其中2枚都是正面朝上有1种,
教师展示合作探究内容,由学生思考作答,学生点评补充后,教师在开展点评讲解,培养学生主动学习意识与合作交流精神
教师展示问题,学生归纳
五、理解应用:
1、口袋中放有3个红球和11个黄球,这两种球除颜色外没有任何区别。
随机从口袋中任取一个球。取到红球或黄球的概率分别是多少?
2、从一副没有大小王的扑克牌(共52张)中随机抽一张,问:
(1)抽到黑桃K的概率;
(2)抽到红桃的概率;
(3)抽到Q的概率。
3、一间宿舍有4张分上下铺的单人床,可安排8名同学住宿。小明和小兵
同住一间宿舍,因为小兵小,大家一致同意他睡下铺,其余同学通过抽签
决定自己的床铺,那么小明抽到 睡上铺的概率是多少?
4、抛掷一个骰子,它落地时向上的的数为
① 2的概率是多少?
②落地时向上的数是3的倍数的概率是多少?
③点数为奇数的概率是多少?
④点数大于2且小于5的数的概率是多少?
教师展示问题,学生作答,教师点评
六、小结:
1、一个随机事件发生的概率P(A)的范围是什么?
必然事件、不可能事件的概率分别是多少?
2、等可能条件下的概率有什么特征?
3、树状图适用于怎样的随机事件?
培养学生归纳梳理的习惯
七、布置作业:
课堂作业:116页复习题2、8
课外作业:自主选做导学测评与同步练习相应内容
巩固所学,培养学生自主学习习惯
第1课时
学习目标:
1、在解决实际问题的过程中,体会随机的思想,
进一步理解概率的意义。
2、理解等可能情形下的随机事件的概率,会运用
列举法计算随机事件的概率。
重点:等可能情形下的所有可能结果的确定
难点:掌握等可能情形下的随机事件的概率的意义
教学方法:三段六步教学法
学习方法:小组化学习
教学准备:班班通畅言系统资源、自制课件、导学案、同步练习
教学过程
一、复习引入:
1.必然事件、不可能事件、随机事件、概率的概念?
2、口答:
(1)投掷一枚均匀的硬币1次,则P(正面朝上)=____;
(2)袋中有6个除颜色外完全相同的小球,其中2个白球,2个黑球,1个红球,1个黄球,从中任意摸出1个球,则 P(白球)=_____ ;P(黑球)=_____;
P(红球)=______;P(黄球)=_______.
二、展示课题与学习目标:
1、在解决实际问题的过程中,体会随机的思想,
进一步理解概率的意义。
2、理解等可能情形下的随机事件的概率,会运用
列举法计算随机事件的概率。
三、自学提纲:
看书95-97页,解决以下问题:
1、计算概率的公式是什么?
2、一个随机事件发生的概率P(A)的范围是什么
必然事件、不可能事件的概率分别是多少
3、树状图有什么特点?
4、自学例1、例2、例3.
自学指导:先独立完成学习任务,再组内交流讨论,汇报收获和疑惑
说一说:
1.从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,有几种可能性,每种的可能性各是多少呢
2.掷一个骰子,向上一面的点数共有几种可能,每种的可能性各是多少?
1,2,3,4,5
1,2,3,4,5,6
教师展示实验,学生思考、交流作答,教师根据情况点评归纳
上面的问题中,都有两个共同的特点:
1)在一次实验中,可能出现的不同结果都只有有限多个.
2) 在一次实验中,各种结果发生的可能性相等.
一般地,如果在一次实验中,有n种可能的结果,并且它们发生的可能性相等,其中使事件A发生的结果数有m( m≤n )种,那么事件A发生的概率为:
当A是必然事件时,m=n, P(A)=1;
当A是不可能事件时,m=0, P(A)=0.
四、合作探究:
1、袋中有3个球,2红1白,除颜色外,其余如材料、大小、
质量等完全相同,随意从中抽出一个球,抽到红球的概率
是多少?
解:
袋中有3个球,随意从中抽一个球,虽然红色、白色球的
个数不等,但每个球被选中的可能性相等。抽出的球共
有三种可能的结果:红(1)、红(2)、白,这三种结
果是“等可能”的。三个结果中有两个结果使事件A(抽
得红球)发生,所以抽得红球的概率是 ,即: P(A)=
(像这样的图,我们称之为树状图,它可以帮助我们不重复、不遗漏地列出一次试验中所有可能出现的结果。)
由树状图知所有可能的结果有4种,其中2枚都是正面朝上有1种,
教师展示合作探究内容,由学生思考作答,学生点评补充后,教师在开展点评讲解,培养学生主动学习意识与合作交流精神
教师展示问题,学生归纳
五、理解应用:
1、口袋中放有3个红球和11个黄球,这两种球除颜色外没有任何区别。
随机从口袋中任取一个球。取到红球或黄球的概率分别是多少?
2、从一副没有大小王的扑克牌(共52张)中随机抽一张,问:
(1)抽到黑桃K的概率;
(2)抽到红桃的概率;
(3)抽到Q的概率。
3、一间宿舍有4张分上下铺的单人床,可安排8名同学住宿。小明和小兵
同住一间宿舍,因为小兵小,大家一致同意他睡下铺,其余同学通过抽签
决定自己的床铺,那么小明抽到 睡上铺的概率是多少?
4、抛掷一个骰子,它落地时向上的的数为
① 2的概率是多少?
②落地时向上的数是3的倍数的概率是多少?
③点数为奇数的概率是多少?
④点数大于2且小于5的数的概率是多少?
教师展示问题,学生作答,教师点评
六、小结:
1、一个随机事件发生的概率P(A)的范围是什么?
必然事件、不可能事件的概率分别是多少?
2、等可能条件下的概率有什么特征?
3、树状图适用于怎样的随机事件?
培养学生归纳梳理的习惯
七、布置作业:
课堂作业:116页复习题2、8
课外作业:自主选做导学测评与同步练习相应内容
巩固所学,培养学生自主学习习惯
