沪科版九年级数学下册 24.6.2正多边形的性质 教案
文档属性
| 名称 | 沪科版九年级数学下册 24.6.2正多边形的性质 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 674.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
§24.6.2正多边形的性质
【教学目标】
知识技能
1.熟练掌握正三角形、正方形、正六边形的有关计算.
2.能用量角器等分圆、尺规等分圆两种方法画正多边形.
数学思考
通过正多边形的有关计算,培养学生的计算能力,特别是解三角形的能力.
解决问题
通过对例题的研究,发展学生的转化思想和解题能力.
情感态度
通过对正三角形、正方形、正六边形的研究,揭示正多边形的内在规律,激发学生的兴趣和探究精神.
【教学重难点】
1.重点:正三角形、正方形、正六边形的有关计算.
2.难点:正确地转化和综合应用几何知识进行计算.
课前延伸
一、基础知识填空
1.正n边形的内角和是____________;
2.正n边形的每个内角等于____________;
3.正n边形的每个外角等于________;
4.正n边形的每个中心角等于________;
5.正n边形的每个内角与它的每个外角的数量关系是________.
二、观察图形,归纳规律问题
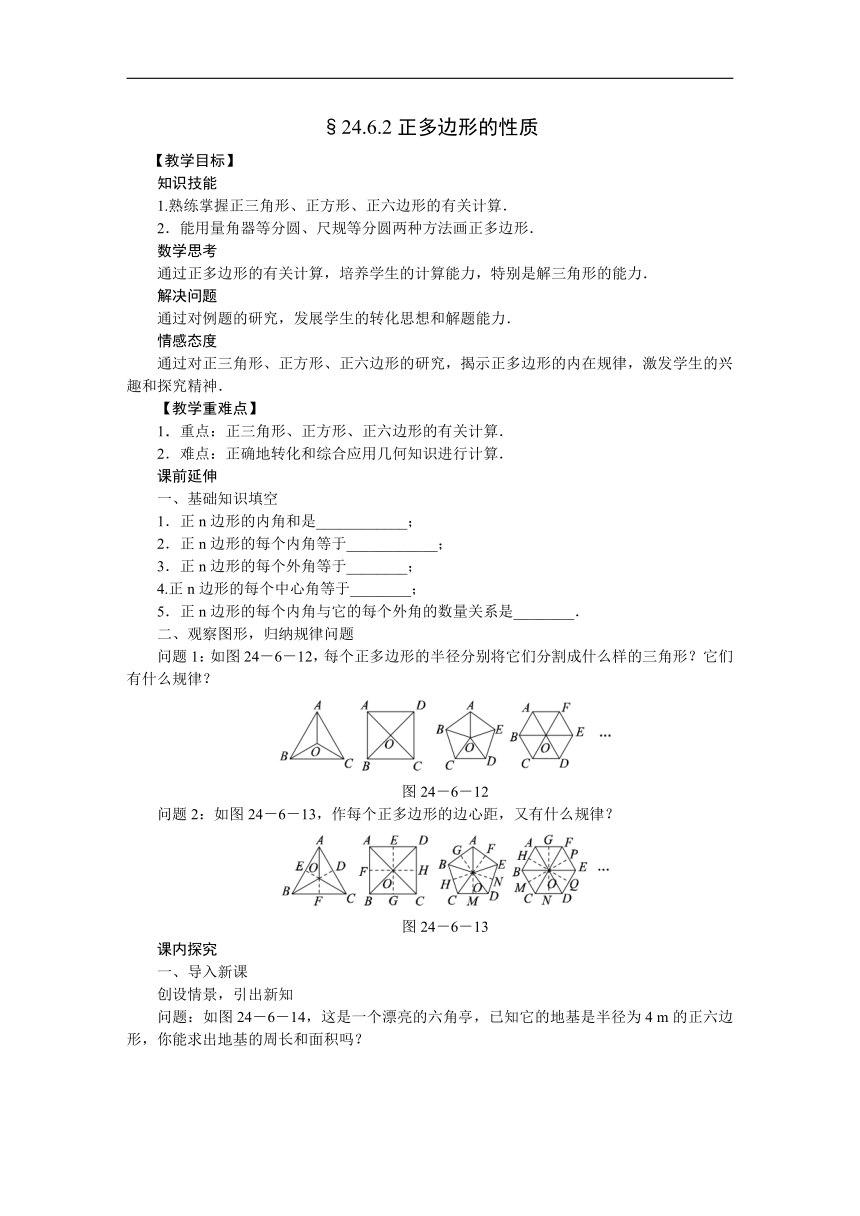
问题1:如图24-6-12,每个正多边形的半径分别将它们分割成什么样的三角形?它们有什么规律?
图24-6-12
问题2:如图24-6-13,作每个正多边形的边心距,又有什么规律?
图24-6-13
课内探究
一、导入新课
创设情景,引出新知
问题:如图24-6-14,这是一个漂亮的六角亭,已知它的地基是半径为4 m的正六边形,你能求出地基的周长和面积吗?
图24-6-14
二、教师精讲点拨
例1 解决六角亭的问题:已知正六边形ABCDEF的半径为4米,求这个正六边形的边长、周长和面积.
例2 请画出一个边长为2厘米的正六边形.
三、学生自主探究
1.下列图形是轴对称图形,但不是中心对称图形的是( )
A.正三角形 B.正方形
C.圆 D.正六边形
2.正六边形的半径与边心距之比为( )
A.1∶ B.∶2
C.2∶ D.∶1
3.已知正三角形的边长为10厘米,则它的边心距为________.
4.正多边形一边所对的中心角与该正多边形的一个内角的关系是________.
5.半径相等的圆内接正三角形、正方形、正六边形的边长之比为________.
6.已知圆内接正方形的边长为2,则该圆的内接正六边形的边长为________.
7.求半径为R的圆内接正三角形的边心距和面积.
四、总结收获
本节课中你最大的收获是什么?请与大家分享.
五、布置作业
教材P52习题24.6第1~8题.
课后提升
1.已知下列图形分别为正方形、正五边形、正六边形,试计算角α4、α5、α6的大小.探究它们存在什么规律?你能证明吗?
图24-6-15
2.已知⊙O的半径为2 cm,求作圆的内接正三角形.
PAGE
【教学目标】
知识技能
1.熟练掌握正三角形、正方形、正六边形的有关计算.
2.能用量角器等分圆、尺规等分圆两种方法画正多边形.
数学思考
通过正多边形的有关计算,培养学生的计算能力,特别是解三角形的能力.
解决问题
通过对例题的研究,发展学生的转化思想和解题能力.
情感态度
通过对正三角形、正方形、正六边形的研究,揭示正多边形的内在规律,激发学生的兴趣和探究精神.
【教学重难点】
1.重点:正三角形、正方形、正六边形的有关计算.
2.难点:正确地转化和综合应用几何知识进行计算.
课前延伸
一、基础知识填空
1.正n边形的内角和是____________;
2.正n边形的每个内角等于____________;
3.正n边形的每个外角等于________;
4.正n边形的每个中心角等于________;
5.正n边形的每个内角与它的每个外角的数量关系是________.
二、观察图形,归纳规律问题
问题1:如图24-6-12,每个正多边形的半径分别将它们分割成什么样的三角形?它们有什么规律?
图24-6-12
问题2:如图24-6-13,作每个正多边形的边心距,又有什么规律?
图24-6-13
课内探究
一、导入新课
创设情景,引出新知
问题:如图24-6-14,这是一个漂亮的六角亭,已知它的地基是半径为4 m的正六边形,你能求出地基的周长和面积吗?
图24-6-14
二、教师精讲点拨
例1 解决六角亭的问题:已知正六边形ABCDEF的半径为4米,求这个正六边形的边长、周长和面积.
例2 请画出一个边长为2厘米的正六边形.
三、学生自主探究
1.下列图形是轴对称图形,但不是中心对称图形的是( )
A.正三角形 B.正方形
C.圆 D.正六边形
2.正六边形的半径与边心距之比为( )
A.1∶ B.∶2
C.2∶ D.∶1
3.已知正三角形的边长为10厘米,则它的边心距为________.
4.正多边形一边所对的中心角与该正多边形的一个内角的关系是________.
5.半径相等的圆内接正三角形、正方形、正六边形的边长之比为________.
6.已知圆内接正方形的边长为2,则该圆的内接正六边形的边长为________.
7.求半径为R的圆内接正三角形的边心距和面积.
四、总结收获
本节课中你最大的收获是什么?请与大家分享.
五、布置作业
教材P52习题24.6第1~8题.
课后提升
1.已知下列图形分别为正方形、正五边形、正六边形,试计算角α4、α5、α6的大小.探究它们存在什么规律?你能证明吗?
图24-6-15
2.已知⊙O的半径为2 cm,求作圆的内接正三角形.
PAGE
