沪科版九年级数学下册 24.1 旋转 教案
文档属性
| 名称 | 沪科版九年级数学下册 24.1 旋转 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 337.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
24.1旋转(1)
教学目标:
1、知识与技能:认识旋转,理解旋转的三要素:旋转中心、旋转方向、旋转角;并能识别在旋转过程中旋转图形的对应点、对应线段和对应角。
2、过程与方法:通过对具体图形旋转过程的观察和抽象,发展学生概括能力和空间想象能力。
3、情感、态度与价值观:通过欣赏生活中的旋转现象,激发学生学习数学的兴趣,体验数学的价值与魅力。
教材分析:
教学重点:理解旋转的定义和识别旋转的三个基本要素。
教学难点:理解、识别旋转的三要素。
教学过程:
创设情境,引入新课
展示生活中的旋转物品:上面情景中的转动现象,有什么共同的特征?
观察抽象,探究新知
什么是图形的旋转?
定点叫什么?转动的角度叫什么?
旋转前后,图形的形状、大小、位置是否发生变化?
归纳:1、在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
2、这个定点称为旋转中心,转动的角称为旋转角。
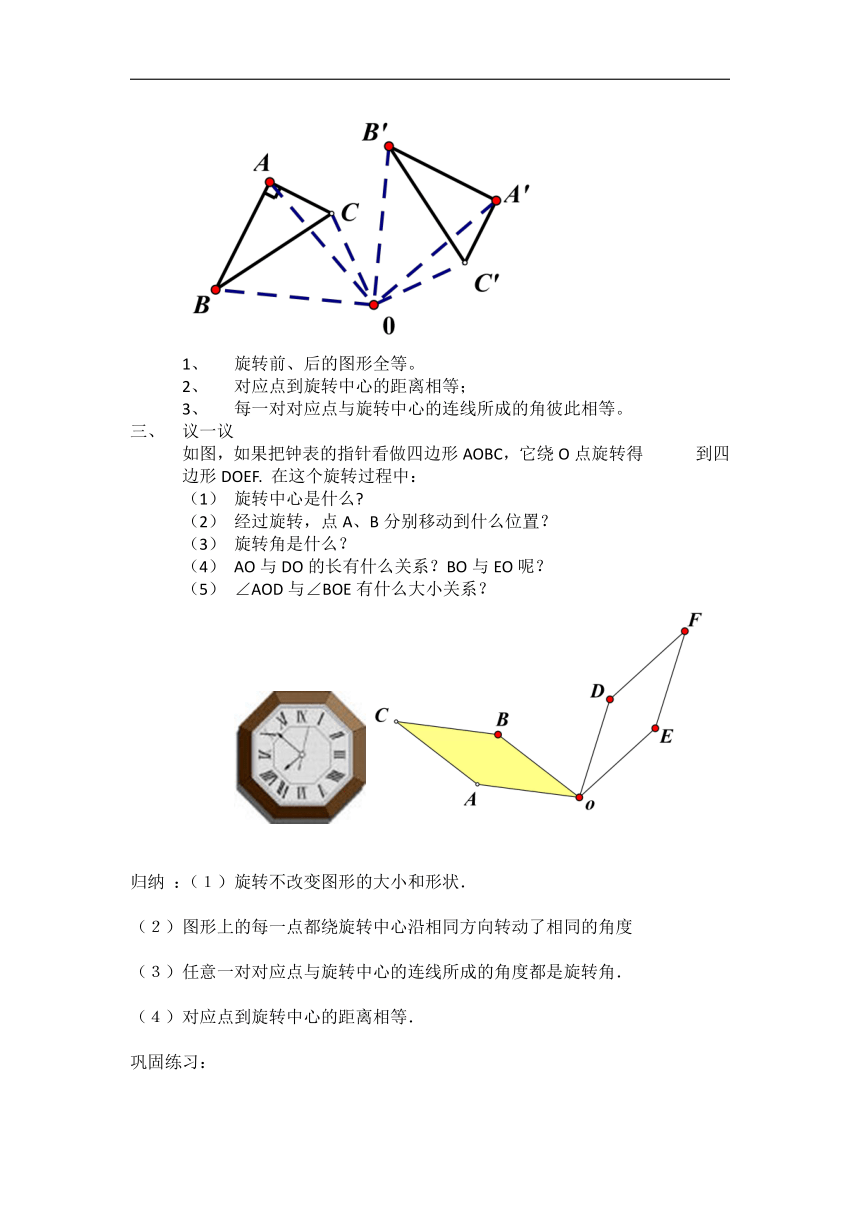
旋转前、后的图形全等。
对应点到旋转中心的距离相等;
每一对对应点与旋转中心的连线所成的角彼此相等。
议一议
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
旋转中心是什么
经过旋转,点A、B分别移动到什么位置?
旋转角是什么?
AO与DO的长有什么关系?BO与EO呢?
∠AOD与∠BOE有什么大小关系?
归纳 :(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
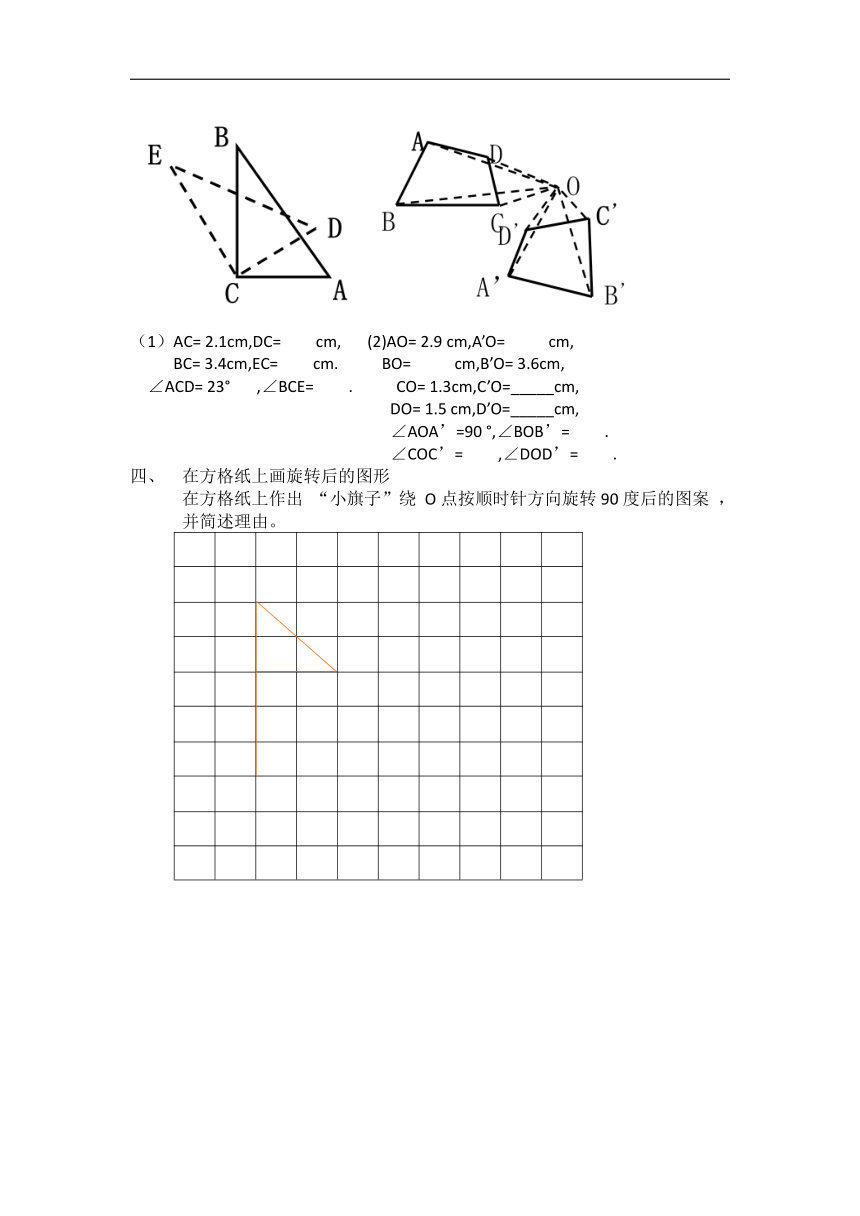
巩固练习:
(1)AC= 2.1cm,DC= cm, (2)AO= 2.9 cm,A’O= cm,
BC= 3.4cm,EC= cm. BO= cm,B’O= 3.6cm,
∠ACD= 23° ,∠BCE= . CO= 1.3cm,C’O=_____cm,
DO= 1.5 cm,D’O=_____cm,
∠AOA’=90 °,∠BOB’= .
∠COC’= ,∠DOD’= .
在方格纸上画旋转后的图形
在方格纸上作出 “小旗子”绕 O点按顺时针方向旋转90度后的图案 ,并简述理由。
已知三角形ABC和点O,画出三角形ABC绕点O按顺时针方向旋转90°后的图形。
例题讲解
例1:钟表的分针匀速旋转一周需要60分.
指出它的旋转中心;
经过20分,分针旋转了多少度?
练习:如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。
旋转中心是哪一点?
旋转了多少度?
点M是AD的中点, 经上述旋转后,点M到什么位置?
连结EF,△AEF是什么三角形
若正方形ABCD的边长是2,
则点M在旋转时经过的路径长是多少?
2、求四边形AFCE的面积。
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?
随堂练习:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
做一做:在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的
课堂回顾:这节课,主要学习了什么?
旋转的概念:在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的性质:1、旋转不改变图形的大小和形状.2、任意一对对应点与旋转中心的连线所成的角度都是旋转角,旋转角相等.3、对应点到旋转中心的距离相等
作业设计
作图:将三角形ABC逆时针绕点O旋转60°
反思:
《图形的旋转》是在继平移、轴对称之后的又一种图形的全等变换,隐含着重要的变换思想,是培养学生思维能力,树立运动变化观点的好素材。本节课的设计本着以观察为起点,以问题为主线,以培养能力为核心的宗旨;遵照教师为主导,学生为主体,训练为主线的教学原则;遵循由特殊到一般,由具体到抽象,由浅到深,由易到难的认知规律。在本节课的教学活动中,我力求通过创设生动、有趣的学习情境,开展观察、比较、操作等系列活动,在活动中帮助学生积极主动的进行探索性学习。同时,我还注重从学生已有知识经验的实际状态出发,大胆地引导学生在探索、验证、交流中学习数学。这一设计充分体现学生的主体地位和教师的主导作用。
这节课上完之后,我感觉成功之处具体表现在以下几方面:
1.创设情境,引人入胜
我首先以有趣的问题引入,激发学生的好奇心,接着播放了一组学生熟悉的有关旋转的画面,极大的吸引了学生的注意力,进而引入课题,最后让学生列举身边有关旋转的例子,并说出它们的共同点,激发学生探索新知的兴趣,为新课的开展创设良好的教学氛围,同时培养学生从数学的角度观察生活,思考问题的能力。
2.过程凸现,紧扣重点
旋转概念的形成过程及旋转性质的得到过程是本节的重点,所以本节突出概念形成过程和性质探究过程的教学。通过列举学生熟悉的例子,从生活问题中抽象出数学本质,引领学生观察、分析归纳,然后提出应该注意问题,帮助学生把握概念的本质特征,再引导学生运用概念解决问题并及时反馈。同时在概念的形成过程中,着重培养学生观察、分析、概括的能力,并引导学生从运动的、变化的角度看问题,向学生渗透辩证唯物主义观点。
3.合作交流,激发兴趣
《数学课程标准》指出:“使学生能够积极参加数学活动,对数学有好奇心与求知欲,并让学生在数学活动中获得成功的体验。”在本节课的教学片段中,我设计的一系列问题串给予小组这样一个争辩活动,目的在于锻炼学生的表达能力、理解能力和思维能力;通过辩论加深了学生对知识的理解,增强了学生学好数学的信心。因此,当学生的思维向更深层次发展并且趋于一致时,及时表扬了学生,由于大家都参与了知识的形成过程,因此所有的学生都体验到了成功的快乐。
4.动态显现,化难为易
在导入新课时,引入生活中的旋转现象及旋转在实际生活中的应用,我都使用了多媒体手段,特别是在探究图形旋转的性质时,在学生经历了实践、观察、总结后,再通过多媒体反复动动态演示,帮助学生形象,直观地理解旋转的性质并加深印象。这样,在教学活动中利用有声、有色、有动感的画面,不仅扣开学生思维之门,也打开了他们心灵之窗,使他们在欣赏、享受中,在美的熏陶中主动地、轻松地、愉快地获得新知。
本节课的不足之处在于:
在教学语言方面,尤其是激励学生的语言还应该更丰富些,以便更好地促进学生的情感、态度等方面的发展。
以上是我对“图形的旋转”这节课的教学反思,在今后的教学中我将查漏补缺、锐意创新,更加深入地学习课程标准,领会课改精神,力求把新的课程理念更好地运用到自己的教学实践中。
教学目标:
1、知识与技能:认识旋转,理解旋转的三要素:旋转中心、旋转方向、旋转角;并能识别在旋转过程中旋转图形的对应点、对应线段和对应角。
2、过程与方法:通过对具体图形旋转过程的观察和抽象,发展学生概括能力和空间想象能力。
3、情感、态度与价值观:通过欣赏生活中的旋转现象,激发学生学习数学的兴趣,体验数学的价值与魅力。
教材分析:
教学重点:理解旋转的定义和识别旋转的三个基本要素。
教学难点:理解、识别旋转的三要素。
教学过程:
创设情境,引入新课
展示生活中的旋转物品:上面情景中的转动现象,有什么共同的特征?
观察抽象,探究新知
什么是图形的旋转?
定点叫什么?转动的角度叫什么?
旋转前后,图形的形状、大小、位置是否发生变化?
归纳:1、在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
2、这个定点称为旋转中心,转动的角称为旋转角。
旋转前、后的图形全等。
对应点到旋转中心的距离相等;
每一对对应点与旋转中心的连线所成的角彼此相等。
议一议
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
旋转中心是什么
经过旋转,点A、B分别移动到什么位置?
旋转角是什么?
AO与DO的长有什么关系?BO与EO呢?
∠AOD与∠BOE有什么大小关系?
归纳 :(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
巩固练习:
(1)AC= 2.1cm,DC= cm, (2)AO= 2.9 cm,A’O= cm,
BC= 3.4cm,EC= cm. BO= cm,B’O= 3.6cm,
∠ACD= 23° ,∠BCE= . CO= 1.3cm,C’O=_____cm,
DO= 1.5 cm,D’O=_____cm,
∠AOA’=90 °,∠BOB’= .
∠COC’= ,∠DOD’= .
在方格纸上画旋转后的图形
在方格纸上作出 “小旗子”绕 O点按顺时针方向旋转90度后的图案 ,并简述理由。
已知三角形ABC和点O,画出三角形ABC绕点O按顺时针方向旋转90°后的图形。
例题讲解
例1:钟表的分针匀速旋转一周需要60分.
指出它的旋转中心;
经过20分,分针旋转了多少度?
练习:如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。
旋转中心是哪一点?
旋转了多少度?
点M是AD的中点, 经上述旋转后,点M到什么位置?
连结EF,△AEF是什么三角形
若正方形ABCD的边长是2,
则点M在旋转时经过的路径长是多少?
2、求四边形AFCE的面积。
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?
随堂练习:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
做一做:在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的
课堂回顾:这节课,主要学习了什么?
旋转的概念:在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的性质:1、旋转不改变图形的大小和形状.2、任意一对对应点与旋转中心的连线所成的角度都是旋转角,旋转角相等.3、对应点到旋转中心的距离相等
作业设计
作图:将三角形ABC逆时针绕点O旋转60°
反思:
《图形的旋转》是在继平移、轴对称之后的又一种图形的全等变换,隐含着重要的变换思想,是培养学生思维能力,树立运动变化观点的好素材。本节课的设计本着以观察为起点,以问题为主线,以培养能力为核心的宗旨;遵照教师为主导,学生为主体,训练为主线的教学原则;遵循由特殊到一般,由具体到抽象,由浅到深,由易到难的认知规律。在本节课的教学活动中,我力求通过创设生动、有趣的学习情境,开展观察、比较、操作等系列活动,在活动中帮助学生积极主动的进行探索性学习。同时,我还注重从学生已有知识经验的实际状态出发,大胆地引导学生在探索、验证、交流中学习数学。这一设计充分体现学生的主体地位和教师的主导作用。
这节课上完之后,我感觉成功之处具体表现在以下几方面:
1.创设情境,引人入胜
我首先以有趣的问题引入,激发学生的好奇心,接着播放了一组学生熟悉的有关旋转的画面,极大的吸引了学生的注意力,进而引入课题,最后让学生列举身边有关旋转的例子,并说出它们的共同点,激发学生探索新知的兴趣,为新课的开展创设良好的教学氛围,同时培养学生从数学的角度观察生活,思考问题的能力。
2.过程凸现,紧扣重点
旋转概念的形成过程及旋转性质的得到过程是本节的重点,所以本节突出概念形成过程和性质探究过程的教学。通过列举学生熟悉的例子,从生活问题中抽象出数学本质,引领学生观察、分析归纳,然后提出应该注意问题,帮助学生把握概念的本质特征,再引导学生运用概念解决问题并及时反馈。同时在概念的形成过程中,着重培养学生观察、分析、概括的能力,并引导学生从运动的、变化的角度看问题,向学生渗透辩证唯物主义观点。
3.合作交流,激发兴趣
《数学课程标准》指出:“使学生能够积极参加数学活动,对数学有好奇心与求知欲,并让学生在数学活动中获得成功的体验。”在本节课的教学片段中,我设计的一系列问题串给予小组这样一个争辩活动,目的在于锻炼学生的表达能力、理解能力和思维能力;通过辩论加深了学生对知识的理解,增强了学生学好数学的信心。因此,当学生的思维向更深层次发展并且趋于一致时,及时表扬了学生,由于大家都参与了知识的形成过程,因此所有的学生都体验到了成功的快乐。
4.动态显现,化难为易
在导入新课时,引入生活中的旋转现象及旋转在实际生活中的应用,我都使用了多媒体手段,特别是在探究图形旋转的性质时,在学生经历了实践、观察、总结后,再通过多媒体反复动动态演示,帮助学生形象,直观地理解旋转的性质并加深印象。这样,在教学活动中利用有声、有色、有动感的画面,不仅扣开学生思维之门,也打开了他们心灵之窗,使他们在欣赏、享受中,在美的熏陶中主动地、轻松地、愉快地获得新知。
本节课的不足之处在于:
在教学语言方面,尤其是激励学生的语言还应该更丰富些,以便更好地促进学生的情感、态度等方面的发展。
以上是我对“图形的旋转”这节课的教学反思,在今后的教学中我将查漏补缺、锐意创新,更加深入地学习课程标准,领会课改精神,力求把新的课程理念更好地运用到自己的教学实践中。
