14解答题(较难题)2021年春上海市各区七年级(下)期末数学知识点分类汇编(含答案)
文档属性
| 名称 | 14解答题(较难题)2021年春上海市各区七年级(下)期末数学知识点分类汇编(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 791.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
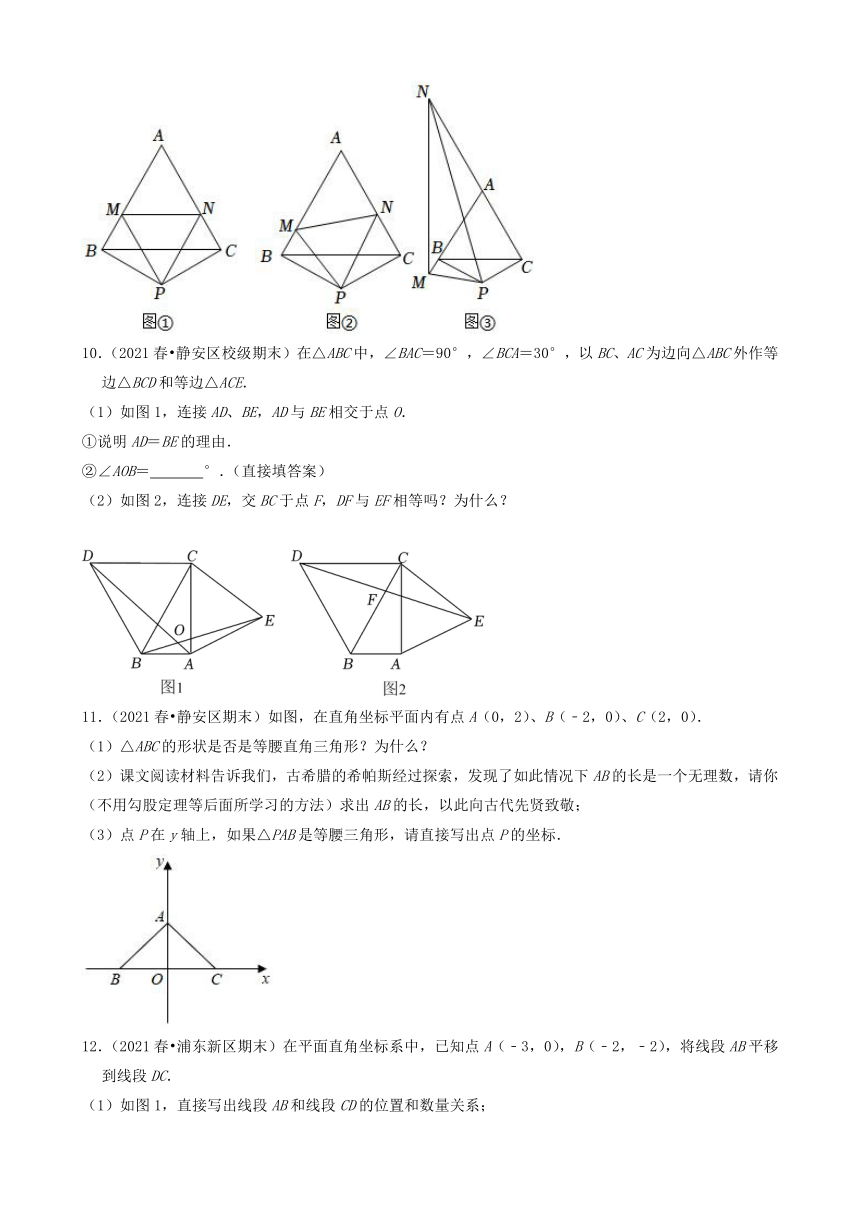
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览


文档简介
14解答题(较难题)
一.三角形的面积(共1小题)
1.(2021春 闵行区期末)在平面直角坐标系xOy中,点A(﹣4,0),点B(0,3),点C(3,0).
(1)△ABC的面积为 ;
(2)已知点D(1,﹣2),E(﹣2,﹣3),那么四边形ACDE的面积为 .
(3)奥地利数学家皮克发现了一类快速求解格点多边形的方法,被称为皮克定理:如果用m表示格点多边形内的格点数,n表示格点多边形边上的格点数,那么格点多边形的面积S和m与n之间满足一种数量关系.例如刚刚求解的几个多边形面积中,我们可以得到如表中信息:
形内格点数m 边界格点数n 格点多边形面积S
△ABC 6 11
四边形ACDE 8 11
五边形ABCDE 20 8
根据上述的例子,猜测皮克公式为S= (用m,n表示),试计算图②中六边形FGHIJK的面积为 (本大题无需写出解题过程,写出正确答案即可).
二.全等三角形的判定与性质(共5小题)
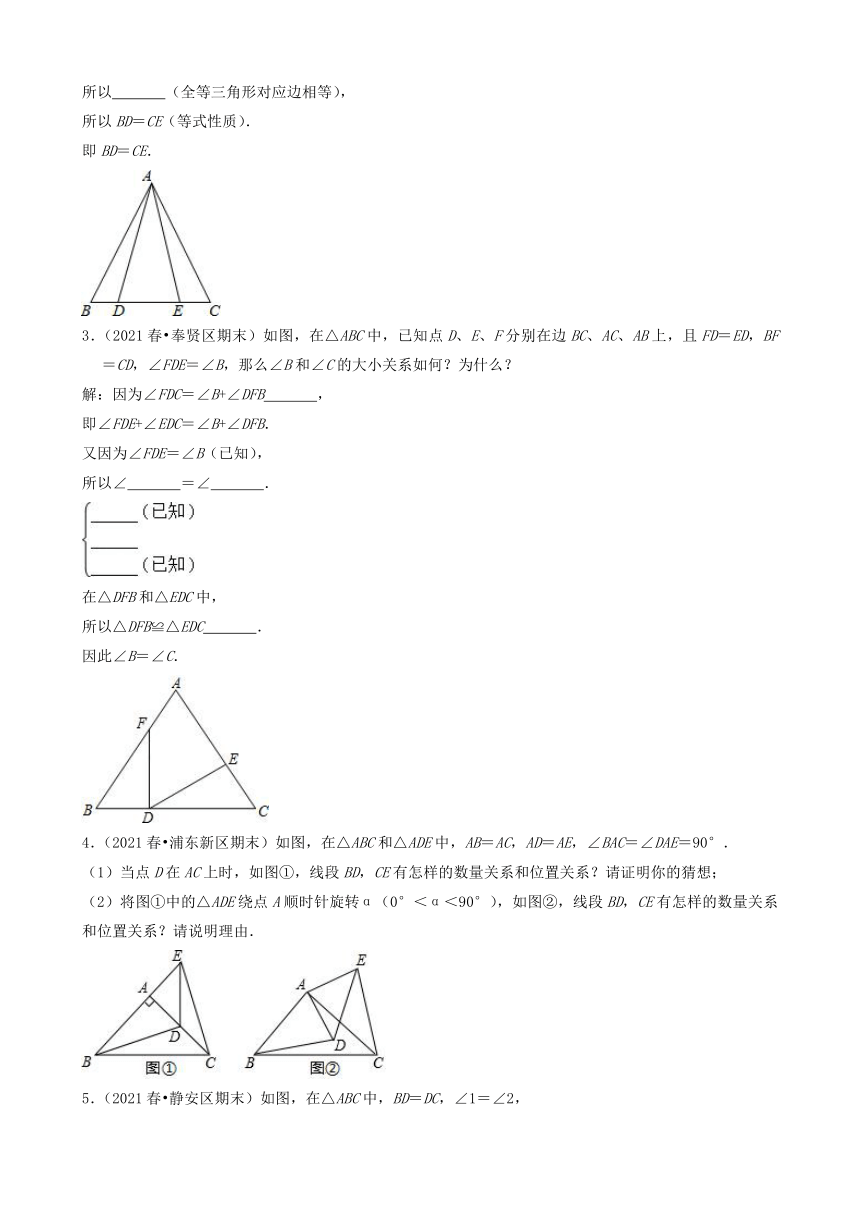
2.(2019春 浦东新区期末)阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
解:因为AB=AC,
所以 (等边对等角).
因为 ,
所以∠AED=∠ADE(等边对等角).
在△ABE与△ACD中,
,
∠AED=∠ADE,
AB=AC
所以△ABE≌△ACD( )
所以 (全等三角形对应边相等),
所以BD=CE(等式性质).
即BD=CE.
3.(2021春 奉贤区期末)如图,在△ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=ED,BF=CD,∠FDE=∠B,那么∠B和∠C的大小关系如何?为什么?
解:因为∠FDC=∠B+∠DFB ,
即∠FDE+∠EDC=∠B+∠DFB.
又因为∠FDE=∠B(已知),
所以∠ =∠ .
在△DFB和△EDC中,
所以△DFB≌△EDC .
因此∠B=∠C.
4.(2021春 浦东新区期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
5.(2021春 静安区期末)如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
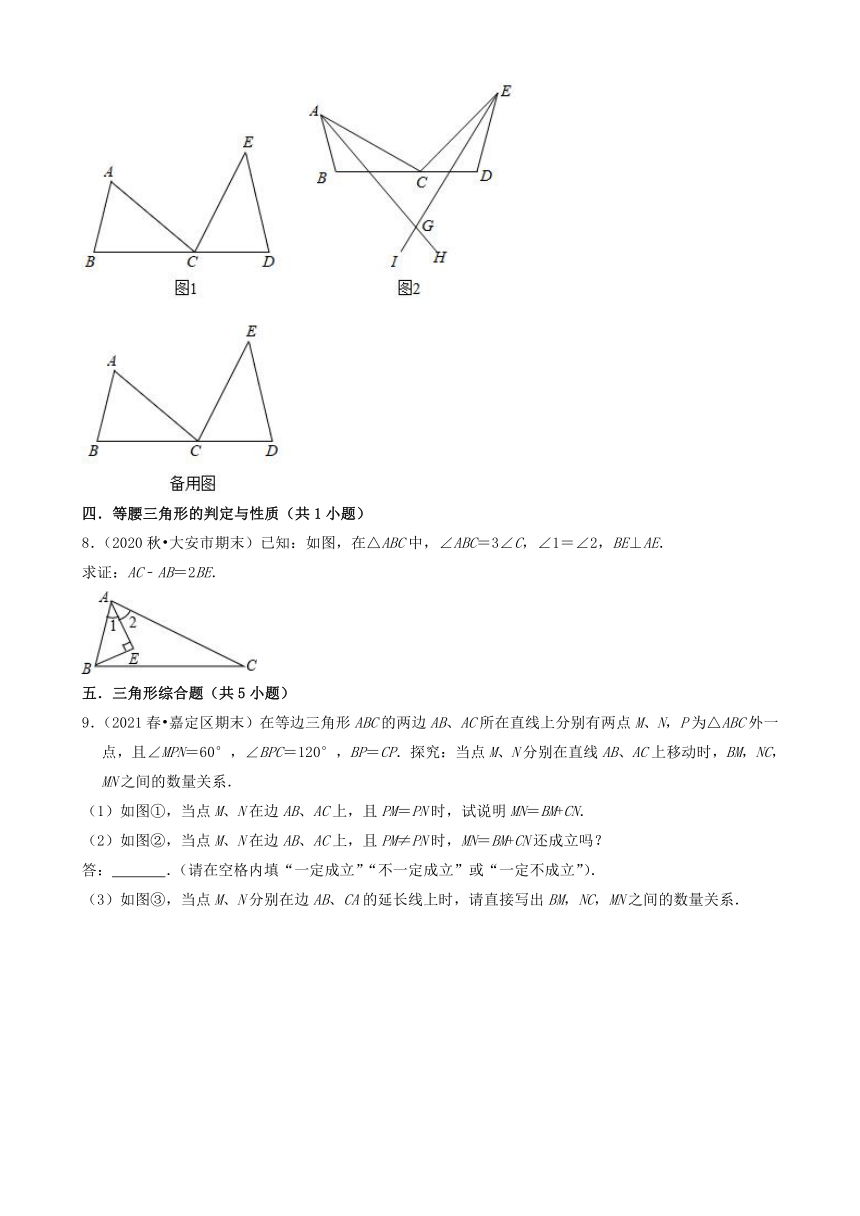
6.(2021春 奉贤区期末)把两个大小不同的等腰直角三角形三角板按照一定的规则放置:“在同一平面内将直角顶点叠合”.
(1)图1是一种放置位置及由它抽象出的几何图形,B、C、D在同一条直线上,连接EC.请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;
(2)图2也是一种放置位置及由它抽象出的几何图形,A、C、D在同一条直线上,连接BD、连接EC并延长与BD交于点F.请找出线段BD和EC的位置关系,并说明理由;
(3)请你:
①画出一个符合放置规则且不同于图1和图2所放位置的几何图形;
②写出你所画几何图形中线段BD和EC的位置和数量关系;
③上面第②题中的结论在按照规则放置所抽象出的几何图形中都存在吗?
三.等腰三角形的性质(共1小题)
7.(2021春 杨浦区期末)已知在△ABC与△CDE中,AB=CD,∠B=∠D,∠ACE=∠B,点B、C、D在同一直线上,射线AH、EI分别平分∠BAC、∠CED.
(1)如图1,试说明AC=CE的理由;
(2)如图2,当AH、EI交于点G时,设∠B=α,∠AGE=β,求β与α的数量关系,并说明理由;
(3)当AH∥EI时,求∠B的度数.
四.等腰三角形的判定与性质(共1小题)
8.(2020秋 大安市期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC﹣AB=2BE.
五.三角形综合题(共5小题)
9.(2021春 嘉定区期末)在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.
(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.
(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?
答: .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.
10.(2021春 静安区校级期末)在△ABC中,∠BAC=90°,∠BCA=30°,以BC、AC为边向△ABC外作等边△BCD和等边△ACE.
(1)如图1,连接AD、BE,AD与BE相交于点O.
①说明AD=BE的理由.
②∠AOB= °.(直接填答案)
(2)如图2,连接DE,交BC于点F,DF与EF相等吗?为什么?
11.(2021春 静安区期末)如图,在直角坐标平面内有点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是否是等腰直角三角形?为什么?
(2)课文阅读材料告诉我们,古希腊的希帕斯经过探索,发现了如此情况下AB的长是一个无理数,请你(不用勾股定理等后面所学习的方法)求出AB的长,以此向古代先贤致敬;
(3)点P在y轴上,如果△PAB是等腰三角形,请直接写出点P的坐标.
12.(2021春 浦东新区期末)在平面直角坐标系中,已知点A(﹣3,0),B(﹣2,﹣2),将线段AB平移到线段DC.
(1)如图1,直接写出线段AB和线段CD的位置和数量关系;
(2)如图2,若线段AB平移到线段DC,D、C两点恰好分别在y轴、x轴上,求点D和点C的坐标;
(3)若点D在y轴的正半轴上,点C在第一象限内,且S△ACD=5,直接写出点C、点D的坐标.
13.(2021春 奉贤区期末)已知△ABC、△AED均为等边三角形,点E是△ABC内的一点.
(1)如图①,说明BD=CE的理由;
(2)如图②,当点E在线段CD上时,∠CDB= 度(直接写出答案);
(3)当△DBE为等腰直角三角形时,∠ABD= 度(直接写出答案).
六.几何变换综合题(共2小题)
14.(2021春 静安区校级期末)已知:等边△ABC边长为3,点D、点E分别在射线AB、射线BC上,且BD=CE=a(0<a<3),将直线DE绕点E顺时针旋转60°,得到直线EF交直线AC于点F.
(1)如图1,当点D在线段AB上,点E在线段BC上时,说明BD+CF=3的理由.
(2)如图2,当点D在线段AB上,点E在线段BC的延长线上时,请判断线段BD,CF之间的数量关系并说明理由.
(3)当点D在线段AB延长线上时,线段BD,CF之间的数量关系又如何?请在备用图中画图探究,并直接写出线段BD,CF之间的数量关系.
15.(2021春 黄浦区期末)如图1,以AB为腰向两侧分别作全等的等腰△ABC和△ABD,过顶角的顶点A作∠NAN,使∠MAN=∠BAC=α(0°<α<60°),将∠MBN的边AM与AC叠合,绕点A按逆时针方向旋转,与射线CB、BD分别交于点E、F.设旋转角度为β.
(1)如图1,当0°<β<α时,说明线段BE=DF的理由;
(2)当α<β<2α时,在图2中画出符合题意的图形并写出此时线段CE、FD与线段BD的数量关系是 .(直接写出答案)
(3)联结EF,在∠MAN绕点A逆时针旋转过程中(0°<β<2α),当线段AD⊥EF时,用含α的代数式表示∠CEA= (直接写出答案).
参考答案与试题解析
一.三角形的面积(共1小题)
1.(2021春 闵行区期末)在平面直角坐标系xOy中,点A(﹣4,0),点B(0,3),点C(3,0).
(1)△ABC的面积为 10.5 ;
(2)已知点D(1,﹣2),E(﹣2,﹣3),那么四边形ACDE的面积为 12.5 .
(3)奥地利数学家皮克发现了一类快速求解格点多边形的方法,被称为皮克定理:如果用m表示格点多边形内的格点数,n表示格点多边形边上的格点数,那么格点多边形的面积S和m与n之间满足一种数量关系.例如刚刚求解的几个多边形面积中,我们可以得到如表中信息:
形内格点数m 边界格点数n 格点多边形面积S
△ABC 6 11
四边形ACDE 8 11
五边形ABCDE 20 8
根据上述的例子,猜测皮克公式为S= m+﹣1 (用m,n表示),试计算图②中六边形FGHIJK的面积为 30 (本大题无需写出解题过程,写出正确答案即可).
【解答】解:(1)根据题意可知:
△ABC的底7,高为3,
所以△ABC的面积为:0.5×7×3=10.5.
故答案为:10.5;
(2)四边形ABCD的面积为:0.5×2×3+3×2+0.5×3×1+0.5×2×2=3+6+1.5+2=12.5.
故答案为:12.5;
(3)根据题意可知:皮克公式为S=m+﹣1,六边形FGHIJK的形内格点数m=27,边界格点数n=8,
所以六边形FGHIJK的面积为27+4﹣1=30.
故答案为:m+﹣1,30.
二.全等三角形的判定与性质(共5小题)
2.(2019春 浦东新区期末)阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
解:因为AB=AC,
所以 ∠B=∠C (等边对等角).
因为 AD=AE ,
所以∠AED=∠ADE(等边对等角).
在△ABE与△ACD中,
∠B=∠C ,
∠AED=∠ADE,
AB=AC
所以△ABE≌△ACD( AAS )
所以 BE=CD (全等三角形对应边相等),
所以BD=CE(等式性质).
即BD=CE.
【解答】解:因为AB=AC,
所以∠B=∠C(等边对等角).
因为 AD=AE,
所以∠AED=∠ADE(等边对等角).
在△ABE与△ACD中,
所以△ABE≌△ACD(AAS),
所以 (全等三角形对应边相等),
所以BD=CE(等式性质).
即BD=CE.
故答案为∠B=∠C,AD=AE,∠B=∠C,AAS,BE=CD.
3.(2021春 奉贤区期末)如图,在△ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=ED,BF=CD,∠FDE=∠B,那么∠B和∠C的大小关系如何?为什么?
解:因为∠FDC=∠B+∠DFB 三角形的一个外角等于与它不相邻的两个内角的和 ,
即∠FDE+∠EDC=∠B+∠DFB.
又因为∠FDE=∠B(已知),
所以∠ DFB =∠ EDC .
在△DFB和△EDC中,
所以△DFB≌△EDC (SAS) .
因此∠B=∠C.
【解答】解:因为∠FDC=∠B+∠DFB(三角形的一个外角等于与它不相邻的两个内角的和),(2分)
即∠FDE+∠EDC=∠B+∠DFB.
又因为∠FDE=∠B(已知),
所以∠DFB=∠EDC.(2分)
,
在△DFB和△EDC中,(2分)
所以△DFB≌△EDC(SAS).(1分)
因此∠B=∠C.
4.(2021春 浦东新区期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
【解答】证明:(1)延长BD交CE于F,
在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠AEC+∠ACE=90°,
∴∠ABD+∠AEC=90°,
∴∠BFE=90°,即EC⊥BD;
(2)延长BD交CE于F,
∵∠BAD+∠CAD=90°,∠CAD+∠EAC=90°,
∴∠BAD=∠EAC,
∵在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABC+∠ACB=90°,
∴∠CBF+∠BCF=∠ABC﹣∠ABD+∠ACB+∠ACE=90°,
∴∠BFC=90°,即EC⊥BD.
5.(2021春 静安区期末)如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
【解答】证明:∵BD=DC,
∴∠DBC=∠DCB,
∵∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD与△ACD中
,
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD是∠BAC的平分线.
6.(2021春 奉贤区期末)把两个大小不同的等腰直角三角形三角板按照一定的规则放置:“在同一平面内将直角顶点叠合”.
(1)图1是一种放置位置及由它抽象出的几何图形,B、C、D在同一条直线上,连接EC.请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;
(2)图2也是一种放置位置及由它抽象出的几何图形,A、C、D在同一条直线上,连接BD、连接EC并延长与BD交于点F.请找出线段BD和EC的位置关系,并说明理由;
(3)请你:
①画出一个符合放置规则且不同于图1和图2所放位置的几何图形;
②写出你所画几何图形中线段BD和EC的位置和数量关系;
③上面第②题中的结论在按照规则放置所抽象出的几何图形中都存在吗?
【解答】解:(1)△ABD≌△ACE.(1分)
∵△ABC是直角三角形,
∴AB=AC,∠BAC=90°.(1分)
同理 AD=AE,∠EAD=90°.(1分)
∴∠BAC=∠EAD.
∴∠BAC+∠CAD=∠EAD+∠CAD.
即∠BAD=∠CAE.(1分)
在△ABD和△ACE中,
∴△ABD≌△ACE.
(2)在△ABD和△ACE中,
∴△ABD≌△ACE.
∴∠ADB=∠AEC.(全等三角形对应角相等)(1分)
∵∠ACE=∠DCF,(对顶角相等)
∠ADB+∠DCF+∠EFD=180°,(三角形内角和180°)
∠AEC+∠ACE+∠EAC=180°,(三角形内角和180°)(1分)
∴∠EAC=∠EFD.(1分)
∵∠BAC=90°,
∴∠EAC=90°.
即∠EFD=90°.
∴BD⊥EC.(垂直定义)(1分)
(3)①如图:(1分)
②BD=EC,BD⊥EC.(2分)
③存在.(1分)
三.等腰三角形的性质(共1小题)
7.(2021春 杨浦区期末)已知在△ABC与△CDE中,AB=CD,∠B=∠D,∠ACE=∠B,点B、C、D在同一直线上,射线AH、EI分别平分∠BAC、∠CED.
(1)如图1,试说明AC=CE的理由;
(2)如图2,当AH、EI交于点G时,设∠B=α,∠AGE=β,求β与α的数量关系,并说明理由;
(3)当AH∥EI时,求∠B的度数.
【解答】(1)证明:∵∠ACD=∠ACE+∠ECD=∠A+∠B,
又∠B=∠ACE,
∴∠A=∠ECD.
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA).
∴AC=CE.
(2)解:3α﹣2β=180°.理由如下:
如图1所示,连接GC并延长至点K.
∵AH、EI分别平分∠BAC、∠DEC,
则设∠CAH=∠BAH=a,∠CEI=∠DEI=b,
∵∠ACK为△ACG的外角,
∴∠ACK=a+∠AGC,
同理可得∠ECK=b+∠EGC,
∴∠ACE=∠ACK+∠ECK=∠B=α
=(a+∠AGC)+(b+∠EGC)=a+b+∠AGE=a+b+β,
即α=a+b+β,
∴a+b=α﹣β.
又由(1)中证明可知∠ECD=∠BAC=2a,
由三角形内角和公式可得∠ECD+∠DEC+∠D=180°,
即2a+2b+α=180°,
∴2(a+b)+α=180°,
∴3α﹣2β=180°.
(3)当AH∥EI时,如图2所示,
过点C作MN∥AH,则MN∥AH∥EI.
∴∠CAH=∠ACM=a,∠CEI=∠ECM=b,
∴∠ACE=∠ACM+∠ECM=a+b=α,即α=a+b.
由(1)中证明可得∠ECD=∠BAC=2a,∠D=∠B=α.
在△CED中,根据三角形内角和定理有∠ECD+∠CED+∠D=180°,
即2a+2b+α=180°,
即2(a+b)=180°﹣α,
即3α=180°,解得:α=60°.
故∠B=60°.
四.等腰三角形的判定与性质(共1小题)
8.(2020秋 大安市期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC﹣AB=2BE.
【解答】证明:延长BE交AC于M
∵BE⊥AE,
∴∠AEB=∠AEM=90°
在△ABE中,
∵∠1+∠3+∠AEB=180°,
∴∠3=90°﹣∠1
同理,∠4=90°﹣∠2
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM
∵BE⊥AE,
∴BM=2BE,
∴AC﹣AB=AC﹣AM=CM,
∵∠4是△BCM的外角
∴∠4=∠5+∠C
∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5
∴3∠C=∠4+∠5=2∠5+∠C
∴∠5=∠C
∴CM=BM
∴AC﹣AB=BM=2BE
五.三角形综合题(共5小题)
9.(2021春 嘉定区期末)在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.
(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.
(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?
答: 一定成立 .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.
【解答】(1)证明:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵∠BPC=120°,BP=CP,
∴∠PBC=∠PCB=×(180°﹣120°)=30°,
∴∠PBM=∠PCN=90°,
在Rt△PBM和Rt△PCN中,
,
∴Rt△PBM≌Rt△PCN(HL),
∴∠BPM=∠CPN=30°,
∵∠MPN=60°,PM=PN,
∴△PMN为等边三角形,
∴PM=PN=MN,
在Rt△PBM中,∠BPM=30°,
∴BM=PM,
同理可得,CN=PN,
∴BM+CN=MN;
(2)解:一定成立,
理由如下:如图②,延长AC至H,使CH=BM,连接PH,
由(1)可知:∠PBM=∠PCN=90°,
∴∠PCH=90°,
∴∠PBM=∠PCH,
在△PBM和△PCH中,
,
∴△PBM≌△PCH(SAS),
∴PM=PH,∠BPM=∠CPH,
∵∠BPM+∠CPN=60°,
∴∠CPN+∠CPH=60°,
∴∠MPN=∠HPN,
在△MPN和△HPN中,
,
∴△MPN≌△HPN(SAS),
∴MN=HN=BM+CN,
故答案为:一定成立;
(3)解:如图③,在AC上截取CK=BM,连接PK,
在△PBM和△PCK中,
,
∴△PBM≌△PCK(SAS),
∴PM=PK,∠BPM=∠CPK,
∵∠BPM+∠BPN=60°,
∴∠CPK+∠BPN=60°,
∴∠KPN=60°,
∴∠MPN=∠KPN,
在△MPN和△KPN中,
,
∴△MPN≌△KPN(SAS),
∴MN=KN,
∵KN=NC﹣CK=NC﹣BM,
∴MN=NC﹣BM.
10.(2021春 静安区校级期末)在△ABC中,∠BAC=90°,∠BCA=30°,以BC、AC为边向△ABC外作等边△BCD和等边△ACE.
(1)如图1,连接AD、BE,AD与BE相交于点O.
①说明AD=BE的理由.
②∠AOB= 120 °.(直接填答案)
(2)如图2,连接DE,交BC于点F,DF与EF相等吗?为什么?
【解答】解:(1)①∵△BCD和△ACE是等边三角形,
∴CB=CD,CA=CE,∠BCD=∠ACE=60°,
∴∠BCD+∠ACB=∠ACE+∠ACB,
即∠DCA=∠BCE,
在△CDA和△CBE中,
,
∴△CDA≌△CBE(SAS),
∴AD=BE.
②设AD与BC交于H,
∵△CDA≌△CBE,
∴∠CDA=∠CBE,
∵∠CDA+∠DHC+∠DCB=180°,∠CBE+∠BHA+∠BOH=180°,∠DHC=∠BHA,
∴∠BOH=∠DCB=60°,
∴∠AOB=180°﹣∠BOH=120°.
故答案为:120;
(2)DF=EF;
理由如下:过E作EM⊥AC交BC于M,交AC于N,
∵△BCD和△ACE是等边三角形,
∴CD=CB,CA=CE=AE,∠DCB=∠AEC=∠ACE=60°,
∵∠ACB=30°,
∴∠DCA=∠ACB+∠DCB=90°,∠ECM=∠ACE+∠ACB=90°,
∵EM⊥AC于N,CE=AE,
∴,∠ENC=90°,
∴∠ACB=∠CEM,
在△CAB和△ECM中,
,
∴△CAB≌△ECM(ASA),
∴CB=EM,
∴CD=EM,
∵∠DCA=∠ENC=90°,
∴CD∥ME,
∴∠DCF=∠EMF,
在△DCF和△EMF,
,
∴△DCF≌△EMF(AAS),
∴DF=EF.
11.(2021春 静安区期末)如图,在直角坐标平面内有点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是否是等腰直角三角形?为什么?
(2)课文阅读材料告诉我们,古希腊的希帕斯经过探索,发现了如此情况下AB的长是一个无理数,请你(不用勾股定理等后面所学习的方法)求出AB的长,以此向古代先贤致敬;
(3)点P在y轴上,如果△PAB是等腰三角形,请直接写出点P的坐标.
【解答】解:(1)△ABC是等腰直角三角形,
理由如下:∵点A(0,2)、B(﹣2,0)、C(2,0),
∴OA=OB=OC=2,
又∵∠AOB=∠AOC=90°,
∴∠ABO=∠BAO=45°,∠ACO=∠CAO=45°,
∴∠BAC=90°,∠ABO=∠ACO,
∴AB=AC,
∴△ABC是等腰直角三角形;
(2)∵S△ABC=×AB×AC=×BC×AO,
∴AB2=4×2=8,
∴AB=2,AB=﹣2(舍去),
∴AB的长为2;
(3)若PB=PA,则点P与点O重合,即点P坐标为(0,0);
若BA=BP=2,且OA⊥OB,
∴OA=OP=2,
∴点P(0,﹣2),
若AB=AP=2,且点A(0,2),
∴点P(0,2+2)或(0,2﹣2),
综上所述:点P的坐标为(0,0)或(0,﹣2)或(0,2+2)或(0,2﹣2).
12.(2021春 浦东新区期末)在平面直角坐标系中,已知点A(﹣3,0),B(﹣2,﹣2),将线段AB平移到线段DC.
(1)如图1,直接写出线段AB和线段CD的位置和数量关系;
(2)如图2,若线段AB平移到线段DC,D、C两点恰好分别在y轴、x轴上,求点D和点C的坐标;
(3)若点D在y轴的正半轴上,点C在第一象限内,且S△ACD=5,直接写出点C、点D的坐标.
【解答】解:(1)由平行的性质可知,线段AB=CD,AB∥CD.
(2)如图2中,过点B作BE⊥x轴,垂足为E,则∠AEB=∠COD=90°,
∵AB∥CD,
∴∠EAB=∠OCD,
在△AEB和△COD中,
∠EAB=∠OCD
,
∴△AEB≌△COD(AAS),
∴AE=CO,BE=DO,
∵A(﹣3,0),B(﹣2,﹣2),
∴AE=CO=1,BE=DO=2,
∴点C坐标为(1,0),点D坐标为(0,2).
(3)如图1中,连接AC,OC.设D(0,m),则C(1,m﹣2).
∵S△ADC=S△AOD+S△OCD﹣S△AOC,
∴5=×3×m+×m×1﹣×3×(m﹣2),
∴m=4,
∴点C(1,2)点D(0,4).
13.(2021春 奉贤区期末)已知△ABC、△AED均为等边三角形,点E是△ABC内的一点.
(1)如图①,说明BD=CE的理由;
(2)如图②,当点E在线段CD上时,∠CDB= 60 度(直接写出答案);
(3)当△DBE为等腰直角三角形时,∠ABD= 15或30或45 度(直接写出答案).
【解答】(1)证明:如图①中,
∵△ABC,△ADE都是等边三角形,
∴AC=AB,AE=AD,∠CAB=∠EAD=60°,
∴∠CAE=∠BAD,
在△CAE和△BAD中,
,
∴△CAE≌△BAD(SAS),
∴CE=BD.
(2)解:如图②中,
由(1)可知△CAE≌△BAD,
∴∠AEC=∠ADB,
∵△ADE是等边三角形,
∴∠AED=∠ADE=60°,
∴∠AEC=∠ADB=120°,
∴∠CDB=∠ADB﹣∠ADE=60°.
故答案为:60.
(3)解:如图③﹣1中,当∠EDB=90°,DE=DB时,
∵△ADE是等边三角形,
∴∠ADE=60°,
∵AD=DE=DB,∠ADB=60°+90°=150°,
∴∠ABD=∠DAB=(180°﹣150°)=15°.
如图③﹣2中,当∠DEB=90°,ED=EB时,同法可得∠EAB=∠EBA=15°,
∵∠EBD=45°,
∴∠ABD=∠EBD﹣∠ABE=45°﹣15°=30°.
如图③﹣3中,当∠EBD=90°,BE=BD时,
∵AE=AD,BE=BD,
∴AB垂直平分线段DE,
∴AB平分∠EBD,
∴∠ABD=45°,
综上所述,满足条件的∠ABD的值为15°或30°或45°.
故答案为:15或30或45.
六.几何变换综合题(共2小题)
14.(2021春 静安区校级期末)已知:等边△ABC边长为3,点D、点E分别在射线AB、射线BC上,且BD=CE=a(0<a<3),将直线DE绕点E顺时针旋转60°,得到直线EF交直线AC于点F.
(1)如图1,当点D在线段AB上,点E在线段BC上时,说明BD+CF=3的理由.
(2)如图2,当点D在线段AB上,点E在线段BC的延长线上时,请判断线段BD,CF之间的数量关系并说明理由.
(3)当点D在线段AB延长线上时,线段BD,CF之间的数量关系又如何?请在备用图中画图探究,并直接写出线段BD,CF之间的数量关系.
【解答】解:(1)∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE且∠DEF﹣60°=∠B,
∴∠BDE=∠FEC,
又∵BD=CE,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD+CF=CE+BE=BC=3;
(2)如下图,设G点在FE的延长线,AF与DE交点为H,
∴∠DEG=∠F+∠FHE=60°,∠BCA=∠FHE+∠BED=60°,
∴∠F=∠BED,
又∵∠B=∠FCE=60°,CE=BD,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD=CE=BE﹣BC=CF﹣BC,
即BD=CF﹣3;
(3)①若E在线段BC上,设DE延长线交AC于点I,
∵∠ABC=∠BDE+∠BED=60°,∠IEF=∠IEC+∠CEF=60°,∠BED=∠IEC,
∴∠BDE=∠CEF,
又∵∠DBE=∠ECF=120°,CE=BD,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD+CF=CE+BE=BC=3;
②若E在BC延长线上,
∵∠ABC=∠BDE+∠BED=60°,∠FED=∠FEC+∠BED=60°,
∴∠BDE=∠FEC,
又∵∠DBE=∠FCE=120°,BD=CE,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴CF﹣BD=BE﹣CE=BC=3;
综上,若E在线段BC上,BD+CF=3;若E在BC延长线上,CF﹣BD=3.
15.(2021春 黄浦区期末)如图1,以AB为腰向两侧分别作全等的等腰△ABC和△ABD,过顶角的顶点A作∠NAN,使∠MAN=∠BAC=α(0°<α<60°),将∠MBN的边AM与AC叠合,绕点A按逆时针方向旋转,与射线CB、BD分别交于点E、F.设旋转角度为β.
(1)如图1,当0°<β<α时,说明线段BE=DF的理由;
(2)当α<β<2α时,在图2中画出符合题意的图形并写出此时线段CE、FD与线段BD的数量关系是 CE﹣FD=BD .(直接写出答案)
(3)联结EF,在∠MAN绕点A逆时针旋转过程中(0°<β<2α),当线段AD⊥EF时,用含α的代数式表示∠CEA= 90°﹣α (直接写出答案).
【解答】解:(1)如图1中,
∵等腰△ABC和△ABD全等,
∴AB=AC=AD,∠C=∠ABC=∠ABD=∠D,∠BAC=∠BAD,
∵∠MAN=∠BAC=α,
∴∠MAN=∠BAD=α,
∴∠EAB=∠FAD,
在△AEB和△AFD中,
,
∴△AEB≌△AFD(ASA),
∴BE=DF.
(2)线段CE、FD与线段BD的数量关系是CE﹣FD=BD,
理由如下:如图2中所示,∵∠MAN=∠BAD,
∴∠DAF=∠BAE,
∵∠ABC=∠ADB,
∴∠ABE=∠ADF,
在△ABE和△ADF中,
,
∴△AEB≌△AFD(ASA),
∴BE=DF,
∵BC=BD,
∴CE﹣FD=CE﹣BE=BC=BD,
故答案为CE﹣FD=BD;
(3)如图3中,设AE交BD于点O,连接EF.
∵∠ABC=∠ADB,
∴∠ABE=∠ADF,
∵AD=AD,∠BAE=∠DAF,
∴△ABE≌△ADF(ASA),
∴AE=AF,
∴∠AFE=∠AEF,
∵∠BAD=∠EAF,∠ABD=∠ADB,
∴∠ABD=∠AFE,
∵AD⊥EF,
∴∠DAF+∠AFE=90°,
∵∠DAF=∠BAE,∠ABD=∠AFE,
∴∠OAB+∠OBA=90°,
∴∠AOB=∠AOF=90°,
∴∠AFD=90°﹣∠EAF=90°﹣α,
∵∠CEA=∠AFD,
∴∠CEA=90°﹣α,
故答案为:90°﹣α.
一.三角形的面积(共1小题)
1.(2021春 闵行区期末)在平面直角坐标系xOy中,点A(﹣4,0),点B(0,3),点C(3,0).
(1)△ABC的面积为 ;
(2)已知点D(1,﹣2),E(﹣2,﹣3),那么四边形ACDE的面积为 .
(3)奥地利数学家皮克发现了一类快速求解格点多边形的方法,被称为皮克定理:如果用m表示格点多边形内的格点数,n表示格点多边形边上的格点数,那么格点多边形的面积S和m与n之间满足一种数量关系.例如刚刚求解的几个多边形面积中,我们可以得到如表中信息:
形内格点数m 边界格点数n 格点多边形面积S
△ABC 6 11
四边形ACDE 8 11
五边形ABCDE 20 8
根据上述的例子,猜测皮克公式为S= (用m,n表示),试计算图②中六边形FGHIJK的面积为 (本大题无需写出解题过程,写出正确答案即可).
二.全等三角形的判定与性质(共5小题)
2.(2019春 浦东新区期末)阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
解:因为AB=AC,
所以 (等边对等角).
因为 ,
所以∠AED=∠ADE(等边对等角).
在△ABE与△ACD中,
,
∠AED=∠ADE,
AB=AC
所以△ABE≌△ACD( )
所以 (全等三角形对应边相等),
所以BD=CE(等式性质).
即BD=CE.
3.(2021春 奉贤区期末)如图,在△ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=ED,BF=CD,∠FDE=∠B,那么∠B和∠C的大小关系如何?为什么?
解:因为∠FDC=∠B+∠DFB ,
即∠FDE+∠EDC=∠B+∠DFB.
又因为∠FDE=∠B(已知),
所以∠ =∠ .
在△DFB和△EDC中,
所以△DFB≌△EDC .
因此∠B=∠C.
4.(2021春 浦东新区期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
5.(2021春 静安区期末)如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
6.(2021春 奉贤区期末)把两个大小不同的等腰直角三角形三角板按照一定的规则放置:“在同一平面内将直角顶点叠合”.
(1)图1是一种放置位置及由它抽象出的几何图形,B、C、D在同一条直线上,连接EC.请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;
(2)图2也是一种放置位置及由它抽象出的几何图形,A、C、D在同一条直线上,连接BD、连接EC并延长与BD交于点F.请找出线段BD和EC的位置关系,并说明理由;
(3)请你:
①画出一个符合放置规则且不同于图1和图2所放位置的几何图形;
②写出你所画几何图形中线段BD和EC的位置和数量关系;
③上面第②题中的结论在按照规则放置所抽象出的几何图形中都存在吗?
三.等腰三角形的性质(共1小题)
7.(2021春 杨浦区期末)已知在△ABC与△CDE中,AB=CD,∠B=∠D,∠ACE=∠B,点B、C、D在同一直线上,射线AH、EI分别平分∠BAC、∠CED.
(1)如图1,试说明AC=CE的理由;
(2)如图2,当AH、EI交于点G时,设∠B=α,∠AGE=β,求β与α的数量关系,并说明理由;
(3)当AH∥EI时,求∠B的度数.
四.等腰三角形的判定与性质(共1小题)
8.(2020秋 大安市期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC﹣AB=2BE.
五.三角形综合题(共5小题)
9.(2021春 嘉定区期末)在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.
(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.
(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?
答: .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.
10.(2021春 静安区校级期末)在△ABC中,∠BAC=90°,∠BCA=30°,以BC、AC为边向△ABC外作等边△BCD和等边△ACE.
(1)如图1,连接AD、BE,AD与BE相交于点O.
①说明AD=BE的理由.
②∠AOB= °.(直接填答案)
(2)如图2,连接DE,交BC于点F,DF与EF相等吗?为什么?
11.(2021春 静安区期末)如图,在直角坐标平面内有点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是否是等腰直角三角形?为什么?
(2)课文阅读材料告诉我们,古希腊的希帕斯经过探索,发现了如此情况下AB的长是一个无理数,请你(不用勾股定理等后面所学习的方法)求出AB的长,以此向古代先贤致敬;
(3)点P在y轴上,如果△PAB是等腰三角形,请直接写出点P的坐标.
12.(2021春 浦东新区期末)在平面直角坐标系中,已知点A(﹣3,0),B(﹣2,﹣2),将线段AB平移到线段DC.
(1)如图1,直接写出线段AB和线段CD的位置和数量关系;
(2)如图2,若线段AB平移到线段DC,D、C两点恰好分别在y轴、x轴上,求点D和点C的坐标;
(3)若点D在y轴的正半轴上,点C在第一象限内,且S△ACD=5,直接写出点C、点D的坐标.
13.(2021春 奉贤区期末)已知△ABC、△AED均为等边三角形,点E是△ABC内的一点.
(1)如图①,说明BD=CE的理由;
(2)如图②,当点E在线段CD上时,∠CDB= 度(直接写出答案);
(3)当△DBE为等腰直角三角形时,∠ABD= 度(直接写出答案).
六.几何变换综合题(共2小题)
14.(2021春 静安区校级期末)已知:等边△ABC边长为3,点D、点E分别在射线AB、射线BC上,且BD=CE=a(0<a<3),将直线DE绕点E顺时针旋转60°,得到直线EF交直线AC于点F.
(1)如图1,当点D在线段AB上,点E在线段BC上时,说明BD+CF=3的理由.
(2)如图2,当点D在线段AB上,点E在线段BC的延长线上时,请判断线段BD,CF之间的数量关系并说明理由.
(3)当点D在线段AB延长线上时,线段BD,CF之间的数量关系又如何?请在备用图中画图探究,并直接写出线段BD,CF之间的数量关系.
15.(2021春 黄浦区期末)如图1,以AB为腰向两侧分别作全等的等腰△ABC和△ABD,过顶角的顶点A作∠NAN,使∠MAN=∠BAC=α(0°<α<60°),将∠MBN的边AM与AC叠合,绕点A按逆时针方向旋转,与射线CB、BD分别交于点E、F.设旋转角度为β.
(1)如图1,当0°<β<α时,说明线段BE=DF的理由;
(2)当α<β<2α时,在图2中画出符合题意的图形并写出此时线段CE、FD与线段BD的数量关系是 .(直接写出答案)
(3)联结EF,在∠MAN绕点A逆时针旋转过程中(0°<β<2α),当线段AD⊥EF时,用含α的代数式表示∠CEA= (直接写出答案).
参考答案与试题解析
一.三角形的面积(共1小题)
1.(2021春 闵行区期末)在平面直角坐标系xOy中,点A(﹣4,0),点B(0,3),点C(3,0).
(1)△ABC的面积为 10.5 ;
(2)已知点D(1,﹣2),E(﹣2,﹣3),那么四边形ACDE的面积为 12.5 .
(3)奥地利数学家皮克发现了一类快速求解格点多边形的方法,被称为皮克定理:如果用m表示格点多边形内的格点数,n表示格点多边形边上的格点数,那么格点多边形的面积S和m与n之间满足一种数量关系.例如刚刚求解的几个多边形面积中,我们可以得到如表中信息:
形内格点数m 边界格点数n 格点多边形面积S
△ABC 6 11
四边形ACDE 8 11
五边形ABCDE 20 8
根据上述的例子,猜测皮克公式为S= m+﹣1 (用m,n表示),试计算图②中六边形FGHIJK的面积为 30 (本大题无需写出解题过程,写出正确答案即可).
【解答】解:(1)根据题意可知:
△ABC的底7,高为3,
所以△ABC的面积为:0.5×7×3=10.5.
故答案为:10.5;
(2)四边形ABCD的面积为:0.5×2×3+3×2+0.5×3×1+0.5×2×2=3+6+1.5+2=12.5.
故答案为:12.5;
(3)根据题意可知:皮克公式为S=m+﹣1,六边形FGHIJK的形内格点数m=27,边界格点数n=8,
所以六边形FGHIJK的面积为27+4﹣1=30.
故答案为:m+﹣1,30.
二.全等三角形的判定与性质(共5小题)
2.(2019春 浦东新区期末)阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
解:因为AB=AC,
所以 ∠B=∠C (等边对等角).
因为 AD=AE ,
所以∠AED=∠ADE(等边对等角).
在△ABE与△ACD中,
∠B=∠C ,
∠AED=∠ADE,
AB=AC
所以△ABE≌△ACD( AAS )
所以 BE=CD (全等三角形对应边相等),
所以BD=CE(等式性质).
即BD=CE.
【解答】解:因为AB=AC,
所以∠B=∠C(等边对等角).
因为 AD=AE,
所以∠AED=∠ADE(等边对等角).
在△ABE与△ACD中,
所以△ABE≌△ACD(AAS),
所以 (全等三角形对应边相等),
所以BD=CE(等式性质).
即BD=CE.
故答案为∠B=∠C,AD=AE,∠B=∠C,AAS,BE=CD.
3.(2021春 奉贤区期末)如图,在△ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=ED,BF=CD,∠FDE=∠B,那么∠B和∠C的大小关系如何?为什么?
解:因为∠FDC=∠B+∠DFB 三角形的一个外角等于与它不相邻的两个内角的和 ,
即∠FDE+∠EDC=∠B+∠DFB.
又因为∠FDE=∠B(已知),
所以∠ DFB =∠ EDC .
在△DFB和△EDC中,
所以△DFB≌△EDC (SAS) .
因此∠B=∠C.
【解答】解:因为∠FDC=∠B+∠DFB(三角形的一个外角等于与它不相邻的两个内角的和),(2分)
即∠FDE+∠EDC=∠B+∠DFB.
又因为∠FDE=∠B(已知),
所以∠DFB=∠EDC.(2分)
,
在△DFB和△EDC中,(2分)
所以△DFB≌△EDC(SAS).(1分)
因此∠B=∠C.
4.(2021春 浦东新区期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
【解答】证明:(1)延长BD交CE于F,
在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠AEC+∠ACE=90°,
∴∠ABD+∠AEC=90°,
∴∠BFE=90°,即EC⊥BD;
(2)延长BD交CE于F,
∵∠BAD+∠CAD=90°,∠CAD+∠EAC=90°,
∴∠BAD=∠EAC,
∵在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABC+∠ACB=90°,
∴∠CBF+∠BCF=∠ABC﹣∠ABD+∠ACB+∠ACE=90°,
∴∠BFC=90°,即EC⊥BD.
5.(2021春 静安区期末)如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
【解答】证明:∵BD=DC,
∴∠DBC=∠DCB,
∵∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD与△ACD中
,
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD是∠BAC的平分线.
6.(2021春 奉贤区期末)把两个大小不同的等腰直角三角形三角板按照一定的规则放置:“在同一平面内将直角顶点叠合”.
(1)图1是一种放置位置及由它抽象出的几何图形,B、C、D在同一条直线上,连接EC.请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;
(2)图2也是一种放置位置及由它抽象出的几何图形,A、C、D在同一条直线上,连接BD、连接EC并延长与BD交于点F.请找出线段BD和EC的位置关系,并说明理由;
(3)请你:
①画出一个符合放置规则且不同于图1和图2所放位置的几何图形;
②写出你所画几何图形中线段BD和EC的位置和数量关系;
③上面第②题中的结论在按照规则放置所抽象出的几何图形中都存在吗?
【解答】解:(1)△ABD≌△ACE.(1分)
∵△ABC是直角三角形,
∴AB=AC,∠BAC=90°.(1分)
同理 AD=AE,∠EAD=90°.(1分)
∴∠BAC=∠EAD.
∴∠BAC+∠CAD=∠EAD+∠CAD.
即∠BAD=∠CAE.(1分)
在△ABD和△ACE中,
∴△ABD≌△ACE.
(2)在△ABD和△ACE中,
∴△ABD≌△ACE.
∴∠ADB=∠AEC.(全等三角形对应角相等)(1分)
∵∠ACE=∠DCF,(对顶角相等)
∠ADB+∠DCF+∠EFD=180°,(三角形内角和180°)
∠AEC+∠ACE+∠EAC=180°,(三角形内角和180°)(1分)
∴∠EAC=∠EFD.(1分)
∵∠BAC=90°,
∴∠EAC=90°.
即∠EFD=90°.
∴BD⊥EC.(垂直定义)(1分)
(3)①如图:(1分)
②BD=EC,BD⊥EC.(2分)
③存在.(1分)
三.等腰三角形的性质(共1小题)
7.(2021春 杨浦区期末)已知在△ABC与△CDE中,AB=CD,∠B=∠D,∠ACE=∠B,点B、C、D在同一直线上,射线AH、EI分别平分∠BAC、∠CED.
(1)如图1,试说明AC=CE的理由;
(2)如图2,当AH、EI交于点G时,设∠B=α,∠AGE=β,求β与α的数量关系,并说明理由;
(3)当AH∥EI时,求∠B的度数.
【解答】(1)证明:∵∠ACD=∠ACE+∠ECD=∠A+∠B,
又∠B=∠ACE,
∴∠A=∠ECD.
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA).
∴AC=CE.
(2)解:3α﹣2β=180°.理由如下:
如图1所示,连接GC并延长至点K.
∵AH、EI分别平分∠BAC、∠DEC,
则设∠CAH=∠BAH=a,∠CEI=∠DEI=b,
∵∠ACK为△ACG的外角,
∴∠ACK=a+∠AGC,
同理可得∠ECK=b+∠EGC,
∴∠ACE=∠ACK+∠ECK=∠B=α
=(a+∠AGC)+(b+∠EGC)=a+b+∠AGE=a+b+β,
即α=a+b+β,
∴a+b=α﹣β.
又由(1)中证明可知∠ECD=∠BAC=2a,
由三角形内角和公式可得∠ECD+∠DEC+∠D=180°,
即2a+2b+α=180°,
∴2(a+b)+α=180°,
∴3α﹣2β=180°.
(3)当AH∥EI时,如图2所示,
过点C作MN∥AH,则MN∥AH∥EI.
∴∠CAH=∠ACM=a,∠CEI=∠ECM=b,
∴∠ACE=∠ACM+∠ECM=a+b=α,即α=a+b.
由(1)中证明可得∠ECD=∠BAC=2a,∠D=∠B=α.
在△CED中,根据三角形内角和定理有∠ECD+∠CED+∠D=180°,
即2a+2b+α=180°,
即2(a+b)=180°﹣α,
即3α=180°,解得:α=60°.
故∠B=60°.
四.等腰三角形的判定与性质(共1小题)
8.(2020秋 大安市期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC﹣AB=2BE.
【解答】证明:延长BE交AC于M
∵BE⊥AE,
∴∠AEB=∠AEM=90°
在△ABE中,
∵∠1+∠3+∠AEB=180°,
∴∠3=90°﹣∠1
同理,∠4=90°﹣∠2
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM
∵BE⊥AE,
∴BM=2BE,
∴AC﹣AB=AC﹣AM=CM,
∵∠4是△BCM的外角
∴∠4=∠5+∠C
∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5
∴3∠C=∠4+∠5=2∠5+∠C
∴∠5=∠C
∴CM=BM
∴AC﹣AB=BM=2BE
五.三角形综合题(共5小题)
9.(2021春 嘉定区期末)在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.
(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.
(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?
答: 一定成立 .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.
【解答】(1)证明:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵∠BPC=120°,BP=CP,
∴∠PBC=∠PCB=×(180°﹣120°)=30°,
∴∠PBM=∠PCN=90°,
在Rt△PBM和Rt△PCN中,
,
∴Rt△PBM≌Rt△PCN(HL),
∴∠BPM=∠CPN=30°,
∵∠MPN=60°,PM=PN,
∴△PMN为等边三角形,
∴PM=PN=MN,
在Rt△PBM中,∠BPM=30°,
∴BM=PM,
同理可得,CN=PN,
∴BM+CN=MN;
(2)解:一定成立,
理由如下:如图②,延长AC至H,使CH=BM,连接PH,
由(1)可知:∠PBM=∠PCN=90°,
∴∠PCH=90°,
∴∠PBM=∠PCH,
在△PBM和△PCH中,
,
∴△PBM≌△PCH(SAS),
∴PM=PH,∠BPM=∠CPH,
∵∠BPM+∠CPN=60°,
∴∠CPN+∠CPH=60°,
∴∠MPN=∠HPN,
在△MPN和△HPN中,
,
∴△MPN≌△HPN(SAS),
∴MN=HN=BM+CN,
故答案为:一定成立;
(3)解:如图③,在AC上截取CK=BM,连接PK,
在△PBM和△PCK中,
,
∴△PBM≌△PCK(SAS),
∴PM=PK,∠BPM=∠CPK,
∵∠BPM+∠BPN=60°,
∴∠CPK+∠BPN=60°,
∴∠KPN=60°,
∴∠MPN=∠KPN,
在△MPN和△KPN中,
,
∴△MPN≌△KPN(SAS),
∴MN=KN,
∵KN=NC﹣CK=NC﹣BM,
∴MN=NC﹣BM.
10.(2021春 静安区校级期末)在△ABC中,∠BAC=90°,∠BCA=30°,以BC、AC为边向△ABC外作等边△BCD和等边△ACE.
(1)如图1,连接AD、BE,AD与BE相交于点O.
①说明AD=BE的理由.
②∠AOB= 120 °.(直接填答案)
(2)如图2,连接DE,交BC于点F,DF与EF相等吗?为什么?
【解答】解:(1)①∵△BCD和△ACE是等边三角形,
∴CB=CD,CA=CE,∠BCD=∠ACE=60°,
∴∠BCD+∠ACB=∠ACE+∠ACB,
即∠DCA=∠BCE,
在△CDA和△CBE中,
,
∴△CDA≌△CBE(SAS),
∴AD=BE.
②设AD与BC交于H,
∵△CDA≌△CBE,
∴∠CDA=∠CBE,
∵∠CDA+∠DHC+∠DCB=180°,∠CBE+∠BHA+∠BOH=180°,∠DHC=∠BHA,
∴∠BOH=∠DCB=60°,
∴∠AOB=180°﹣∠BOH=120°.
故答案为:120;
(2)DF=EF;
理由如下:过E作EM⊥AC交BC于M,交AC于N,
∵△BCD和△ACE是等边三角形,
∴CD=CB,CA=CE=AE,∠DCB=∠AEC=∠ACE=60°,
∵∠ACB=30°,
∴∠DCA=∠ACB+∠DCB=90°,∠ECM=∠ACE+∠ACB=90°,
∵EM⊥AC于N,CE=AE,
∴,∠ENC=90°,
∴∠ACB=∠CEM,
在△CAB和△ECM中,
,
∴△CAB≌△ECM(ASA),
∴CB=EM,
∴CD=EM,
∵∠DCA=∠ENC=90°,
∴CD∥ME,
∴∠DCF=∠EMF,
在△DCF和△EMF,
,
∴△DCF≌△EMF(AAS),
∴DF=EF.
11.(2021春 静安区期末)如图,在直角坐标平面内有点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是否是等腰直角三角形?为什么?
(2)课文阅读材料告诉我们,古希腊的希帕斯经过探索,发现了如此情况下AB的长是一个无理数,请你(不用勾股定理等后面所学习的方法)求出AB的长,以此向古代先贤致敬;
(3)点P在y轴上,如果△PAB是等腰三角形,请直接写出点P的坐标.
【解答】解:(1)△ABC是等腰直角三角形,
理由如下:∵点A(0,2)、B(﹣2,0)、C(2,0),
∴OA=OB=OC=2,
又∵∠AOB=∠AOC=90°,
∴∠ABO=∠BAO=45°,∠ACO=∠CAO=45°,
∴∠BAC=90°,∠ABO=∠ACO,
∴AB=AC,
∴△ABC是等腰直角三角形;
(2)∵S△ABC=×AB×AC=×BC×AO,
∴AB2=4×2=8,
∴AB=2,AB=﹣2(舍去),
∴AB的长为2;
(3)若PB=PA,则点P与点O重合,即点P坐标为(0,0);
若BA=BP=2,且OA⊥OB,
∴OA=OP=2,
∴点P(0,﹣2),
若AB=AP=2,且点A(0,2),
∴点P(0,2+2)或(0,2﹣2),
综上所述:点P的坐标为(0,0)或(0,﹣2)或(0,2+2)或(0,2﹣2).
12.(2021春 浦东新区期末)在平面直角坐标系中,已知点A(﹣3,0),B(﹣2,﹣2),将线段AB平移到线段DC.
(1)如图1,直接写出线段AB和线段CD的位置和数量关系;
(2)如图2,若线段AB平移到线段DC,D、C两点恰好分别在y轴、x轴上,求点D和点C的坐标;
(3)若点D在y轴的正半轴上,点C在第一象限内,且S△ACD=5,直接写出点C、点D的坐标.
【解答】解:(1)由平行的性质可知,线段AB=CD,AB∥CD.
(2)如图2中,过点B作BE⊥x轴,垂足为E,则∠AEB=∠COD=90°,
∵AB∥CD,
∴∠EAB=∠OCD,
在△AEB和△COD中,
∠EAB=∠OCD
,
∴△AEB≌△COD(AAS),
∴AE=CO,BE=DO,
∵A(﹣3,0),B(﹣2,﹣2),
∴AE=CO=1,BE=DO=2,
∴点C坐标为(1,0),点D坐标为(0,2).
(3)如图1中,连接AC,OC.设D(0,m),则C(1,m﹣2).
∵S△ADC=S△AOD+S△OCD﹣S△AOC,
∴5=×3×m+×m×1﹣×3×(m﹣2),
∴m=4,
∴点C(1,2)点D(0,4).
13.(2021春 奉贤区期末)已知△ABC、△AED均为等边三角形,点E是△ABC内的一点.
(1)如图①,说明BD=CE的理由;
(2)如图②,当点E在线段CD上时,∠CDB= 60 度(直接写出答案);
(3)当△DBE为等腰直角三角形时,∠ABD= 15或30或45 度(直接写出答案).
【解答】(1)证明:如图①中,
∵△ABC,△ADE都是等边三角形,
∴AC=AB,AE=AD,∠CAB=∠EAD=60°,
∴∠CAE=∠BAD,
在△CAE和△BAD中,
,
∴△CAE≌△BAD(SAS),
∴CE=BD.
(2)解:如图②中,
由(1)可知△CAE≌△BAD,
∴∠AEC=∠ADB,
∵△ADE是等边三角形,
∴∠AED=∠ADE=60°,
∴∠AEC=∠ADB=120°,
∴∠CDB=∠ADB﹣∠ADE=60°.
故答案为:60.
(3)解:如图③﹣1中,当∠EDB=90°,DE=DB时,
∵△ADE是等边三角形,
∴∠ADE=60°,
∵AD=DE=DB,∠ADB=60°+90°=150°,
∴∠ABD=∠DAB=(180°﹣150°)=15°.
如图③﹣2中,当∠DEB=90°,ED=EB时,同法可得∠EAB=∠EBA=15°,
∵∠EBD=45°,
∴∠ABD=∠EBD﹣∠ABE=45°﹣15°=30°.
如图③﹣3中,当∠EBD=90°,BE=BD时,
∵AE=AD,BE=BD,
∴AB垂直平分线段DE,
∴AB平分∠EBD,
∴∠ABD=45°,
综上所述,满足条件的∠ABD的值为15°或30°或45°.
故答案为:15或30或45.
六.几何变换综合题(共2小题)
14.(2021春 静安区校级期末)已知:等边△ABC边长为3,点D、点E分别在射线AB、射线BC上,且BD=CE=a(0<a<3),将直线DE绕点E顺时针旋转60°,得到直线EF交直线AC于点F.
(1)如图1,当点D在线段AB上,点E在线段BC上时,说明BD+CF=3的理由.
(2)如图2,当点D在线段AB上,点E在线段BC的延长线上时,请判断线段BD,CF之间的数量关系并说明理由.
(3)当点D在线段AB延长线上时,线段BD,CF之间的数量关系又如何?请在备用图中画图探究,并直接写出线段BD,CF之间的数量关系.
【解答】解:(1)∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE且∠DEF﹣60°=∠B,
∴∠BDE=∠FEC,
又∵BD=CE,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD+CF=CE+BE=BC=3;
(2)如下图,设G点在FE的延长线,AF与DE交点为H,
∴∠DEG=∠F+∠FHE=60°,∠BCA=∠FHE+∠BED=60°,
∴∠F=∠BED,
又∵∠B=∠FCE=60°,CE=BD,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD=CE=BE﹣BC=CF﹣BC,
即BD=CF﹣3;
(3)①若E在线段BC上,设DE延长线交AC于点I,
∵∠ABC=∠BDE+∠BED=60°,∠IEF=∠IEC+∠CEF=60°,∠BED=∠IEC,
∴∠BDE=∠CEF,
又∵∠DBE=∠ECF=120°,CE=BD,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD+CF=CE+BE=BC=3;
②若E在BC延长线上,
∵∠ABC=∠BDE+∠BED=60°,∠FED=∠FEC+∠BED=60°,
∴∠BDE=∠FEC,
又∵∠DBE=∠FCE=120°,BD=CE,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴CF﹣BD=BE﹣CE=BC=3;
综上,若E在线段BC上,BD+CF=3;若E在BC延长线上,CF﹣BD=3.
15.(2021春 黄浦区期末)如图1,以AB为腰向两侧分别作全等的等腰△ABC和△ABD,过顶角的顶点A作∠NAN,使∠MAN=∠BAC=α(0°<α<60°),将∠MBN的边AM与AC叠合,绕点A按逆时针方向旋转,与射线CB、BD分别交于点E、F.设旋转角度为β.
(1)如图1,当0°<β<α时,说明线段BE=DF的理由;
(2)当α<β<2α时,在图2中画出符合题意的图形并写出此时线段CE、FD与线段BD的数量关系是 CE﹣FD=BD .(直接写出答案)
(3)联结EF,在∠MAN绕点A逆时针旋转过程中(0°<β<2α),当线段AD⊥EF时,用含α的代数式表示∠CEA= 90°﹣α (直接写出答案).
【解答】解:(1)如图1中,
∵等腰△ABC和△ABD全等,
∴AB=AC=AD,∠C=∠ABC=∠ABD=∠D,∠BAC=∠BAD,
∵∠MAN=∠BAC=α,
∴∠MAN=∠BAD=α,
∴∠EAB=∠FAD,
在△AEB和△AFD中,
,
∴△AEB≌△AFD(ASA),
∴BE=DF.
(2)线段CE、FD与线段BD的数量关系是CE﹣FD=BD,
理由如下:如图2中所示,∵∠MAN=∠BAD,
∴∠DAF=∠BAE,
∵∠ABC=∠ADB,
∴∠ABE=∠ADF,
在△ABE和△ADF中,
,
∴△AEB≌△AFD(ASA),
∴BE=DF,
∵BC=BD,
∴CE﹣FD=CE﹣BE=BC=BD,
故答案为CE﹣FD=BD;
(3)如图3中,设AE交BD于点O,连接EF.
∵∠ABC=∠ADB,
∴∠ABE=∠ADF,
∵AD=AD,∠BAE=∠DAF,
∴△ABE≌△ADF(ASA),
∴AE=AF,
∴∠AFE=∠AEF,
∵∠BAD=∠EAF,∠ABD=∠ADB,
∴∠ABD=∠AFE,
∵AD⊥EF,
∴∠DAF+∠AFE=90°,
∵∠DAF=∠BAE,∠ABD=∠AFE,
∴∠OAB+∠OBA=90°,
∴∠AOB=∠AOF=90°,
∴∠AFD=90°﹣∠EAF=90°﹣α,
∵∠CEA=∠AFD,
∴∠CEA=90°﹣α,
故答案为:90°﹣α.
同课章节目录
