12解答题(中档题)(含解析)-2021年春上海市各区七年级(下)期末数学知识点分类汇编
文档属性
| 名称 | 12解答题(中档题)(含解析)-2021年春上海市各区七年级(下)期末数学知识点分类汇编 |

|
|
| 格式 | doc | ||
| 文件大小 | 661.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 00:00:00 | ||
图片预览




文档简介
12解答题(中档题)
一.平方根(共1小题)
1.(2021春 浦东新区期末)一个正数x的两个不同的平方根分别是2a﹣1和﹣a+2.
(1)求a和x的值;
(2)求3x+2a的平方根.
二.实数的运算(共6小题)
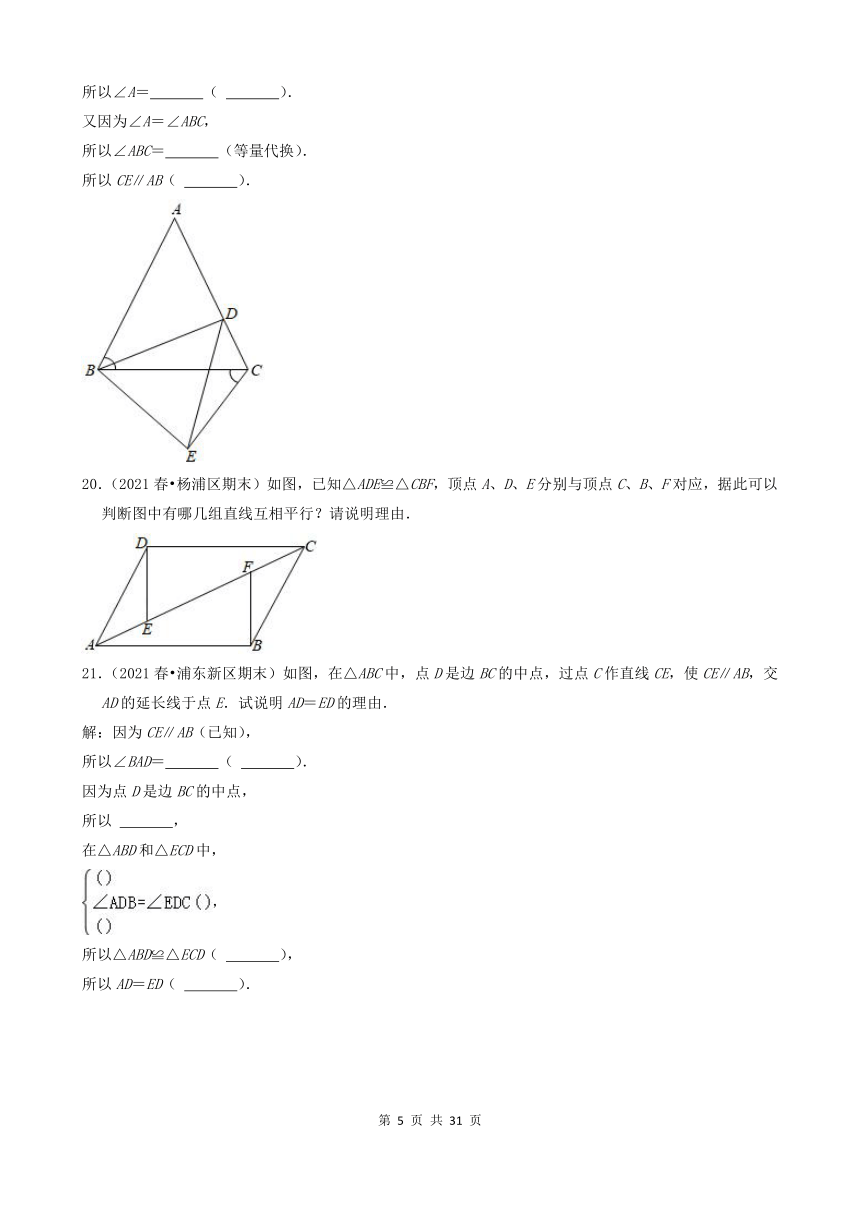
2.(2021春 浦东新区期末)计算:
.
3.(2021春 嘉定区期末)用幂的运算性质计算:(结果表示为含幂的形式).
4.(2021春 奉贤区期末)计算:.
5.(2021春 奉贤区期末)利用幂的运算性质计算:﹣×÷(结果用幂的形式表示).
6.(2021春 杨浦区期末)用幂的运算性质计算:(结果表示为含幂的形式).
7.(2021春 黄浦区期末)利用幂的运算性质计算:.
三.分数指数幂(共1小题)
8.(2021春 静安区期末)用幂的性质计算:(5﹣17) (5+17).
四.二次根式的乘除法(共1小题)
9.(2021春 黄浦区期末)计算:.
五.二次根式的混合运算(共1小题)
10.(2021春 奉贤区期末)计算:(3﹣2)×+(﹣)2.
六.一次函数图象上点的坐标特征(共1小题)
11.(2021春 杨浦区期末)如图,在平面直角坐标系中,点A(﹣2,﹣3),点A关于x轴的对称点记作点B,将点B向右平移2个单位得点C.
(1)分别写出点B、C的坐标:B( )、C( );
(2)点D在x轴的正半轴上,点E在直线y=1上,如果△CDE是以CD为腰的等腰直角三角形,那么点E的坐标是 .
七.平行线的判定(共1小题)
12.(2021春 奉贤区期末)如图,已知AE平分∠BAC交BC于点E,AF平分∠CAD交BC的延长线于点F,∠B=64°,∠EAF=58°,试判断AD与BC是否平行.
解:∵AE平分∠BAC,AF平分∠CAD(已知),
∴∠BAC=2∠1,∠CAD= ( ).
又∵∠EAF=∠1+∠2=58°,
∴∠BAD=∠BAC+∠CAD
=2(∠1+∠2)
= °(等式性质).
又∵∠B=64°(已知),
∴∠BAD+∠B= °.
∴ ∥ ( ).
八.平行线的判定与性质(共1小题)
13.(2021春 静安区期末)如图,已知在△ABC中,FG∥EB,∠2=∠3,说明∠EDB+∠DBC=180°的理由.
解:∵FG∥EB( ),
∴ = ( ).
∵∠2=∠3(已知),
∴ = ( ).
∴DE∥BC( ),
∴∠EDB+∠DBC=180°( ).
九.三角形内角和定理(共2小题)
14.(2021春 金山区期末)如图,在△ABC中,∠A=20°,∠B=60°,CD平分∠ACB交AB边于点D,求∠CDB的度数.
15.(2021春 邗江区期末)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为 °,△AOB .(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC (填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
一十.全等三角形的判定与性质(共18小题)
16.(2021春 奉贤区期末)如图,已知AD=BC,AE=BE,说明AC=BD的理由.
17.(2021春 浦东新区期末)如图,在△ABC中,E是AD上的一点,EB=EC,∠ABE=∠ACE,请说明AD⊥BC.
解:因为EB=EC(已知),
所以∠EBC=∠ECB( ).
又因为∠ABE=∠ACE(已知),
所以∠ABE+∠EBC=∠ACE+∠ECB( ).
即∠ABC=∠ACB.
所以AB=AC( ).
在△ABE和△ACE中,
所以△ABE≌△ACE( ).
得∠BAD=∠CAD( ).
所以AD⊥BC( ).
18.(2021春 浦东新区期末)如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
19.(2021春 杨浦区期末)如图,已知△ABC与△BDE都是等边三角形,点D在边AC上,说明CE∥AB的理由.
解:因为△ABC是等边三角形(已知),
所以∠A=∠ABC=60°,AB=BC(等边三角形的意义).
因为△BDE是等边三角形(已知),
所以∠DBE=60°,BD=BE(等边三角形的意义).
所以∠ABC﹣∠DBC=∠DBE﹣∠DBC(等式性质),
得∠ABD= .
在△ABD与△CBE中,,
所以△ABD≌△CBE( ).
所以∠A= ( ).
又因为∠A=∠ABC,
所以∠ABC= (等量代换).
所以CE∥AB( ).
20.(2021春 杨浦区期末)如图,已知△ADE≌△CBF,顶点A、D、E分别与顶点C、B、F对应,据此可以判断图中有哪几组直线互相平行?请说明理由.
21.(2021春 浦东新区期末)如图,在△ABC中,点D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.试说明AD=ED的理由.
解:因为CE∥AB(已知),
所以∠BAD= ( ).
因为点D是边BC的中点,
所以 ,
在△ABD和△ECD中,
,
所以△ABD≌△ECD( ),
所以AD=ED( ).
22.(2021春 黄浦区期末)如图,已知在△ABC中,∠ACB=90°,AC=BC,∠A的平分线AD交BC于点D,过点B作BE⊥AD于E.
(1)说明△ACD≌△BCF的理由;
(2)BE与AD的长度关系是 ,请说明理由.
23.(2021春 黄浦区期末)如图在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.
(1)说明△ADE≌△BFE的理由;
(2)联结EG,那么EG与DF的位置关系是 ,请说明理由.
24.(2021春 嘉定区期末)如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
25.(2021春 嘉定区期末)如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AE=BE,AD与BE相交于点F.
(1)请说明△AEF≌△BEC的理由.
(2)如果AF=2BD,试说明AD平分∠BAC的理由.
26.(2021春 静安区校级期末)如图,△ABC中,两条高BD和CE相交于H,已知AB=CH.试判断△BCD的形状并说明理由.
27.(2021春 浦东新区校级期末)如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
28.(2021春 金山区期末)如图,已知△ACM是等边三角形,点E在边CM上,以CE为边作等边△CEF,联结AE并延长交CF的延长线于点N,联结MF并延长交AC的延长线于点B,联结BN.
(1)说明△ACE≌△MCF的理由;
(2)说明△CNB为等边三角形的理由.
29.(2021 永嘉县校级模拟)如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,过点B作BE⊥AC,垂足为E,在线段BE上截取ED=EC,AD的延长线交BC于点P,联结DC.
(1)请说明AD=BC的理由;
(2)请说明BP=PC的理由.
30.(2021春 松江区期末)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠EAF=∠BAD.
(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由;
(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.
31.(2021春 浦东新区期末)已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)求证:CF=CH;
(3)判断△CFH的形状并说明理由.
32.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
33.(2021春 奉贤区期末)如图,在△ABC中,已知D是BC边的中点,过点D的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,交AC的延长线于点E,联结EG.
(1)说明BG与CF相等的理由.
(2)说明∠BGD与∠DGE相等的理由.
参考答案与试题解析
一.平方根(共1小题)
1.(2021春 浦东新区期末)一个正数x的两个不同的平方根分别是2a﹣1和﹣a+2.
(1)求a和x的值;
(2)求3x+2a的平方根.
【解答】解:(1)∵一个正数的两个平方根互为相反数,
∴2a﹣1+(﹣a+2)=0,
解得a=﹣1,
∴x=(2a﹣1)2=(﹣3)2=9.
(2)∵3x+2a=3×9﹣2=25,
∴25的平方根为±5.
二.实数的运算(共6小题)
2.(2021春 浦东新区期末)计算:
.
【解答】解:原式=3﹣4+3﹣﹣1=1﹣.
3.(2021春 嘉定区期末)用幂的运算性质计算:(结果表示为含幂的形式).
【解答】解:原式=4×8÷32
=2×2÷2
=2
=2.
4.(2021春 奉贤区期末)计算:.
【解答】解:原式=2+﹣+1
=2﹣3﹣6+1
=﹣6.
5.(2021春 奉贤区期末)利用幂的运算性质计算:﹣×÷(结果用幂的形式表示).
【解答】解:原式=﹣×(﹣)÷
=×÷
=
=.
6.(2021春 杨浦区期末)用幂的运算性质计算:(结果表示为含幂的形式).
【解答】解:原式=3×9÷81
=3×3÷3
=3
=3.
7.(2021春 黄浦区期末)利用幂的运算性质计算:.
【解答】解:原式=2×2×2×
=2×2
=2×2
=2.
三.分数指数幂(共1小题)
8.(2021春 静安区期末)用幂的性质计算:(5﹣17) (5+17).
【解答】解:原式=[(5﹣)(5+)]
=(25﹣17)
=8
=
=2
四.二次根式的乘除法(共1小题)
9.(2021春 黄浦区期末)计算:.
【解答】解:原式=××2×
=1.
五.二次根式的混合运算(共1小题)
10.(2021春 奉贤区期末)计算:(3﹣2)×+(﹣)2.
【解答】解:原式=3﹣6+(2+3﹣2)
=3﹣6+5﹣2
=﹣1.
六.一次函数图象上点的坐标特征(共1小题)
11.(2021春 杨浦区期末)如图,在平面直角坐标系中,点A(﹣2,﹣3),点A关于x轴的对称点记作点B,将点B向右平移2个单位得点C.
(1)分别写出点B、C的坐标:B( ﹣2,3 )、C( 0,3 );
(2)点D在x轴的正半轴上,点E在直线y=1上,如果△CDE是以CD为腰的等腰直角三角形,那么点E的坐标是 (﹣1,1) .
【解答】解:(1)∵将点A(﹣2,﹣3)关于x轴的对称点B的坐标为(﹣2,3),
将点B向右平移2个单位得点C,
∴C(0,3),
故答案为﹣2,3;0,3;
(2)作EF⊥x轴于F,
由题意可知,△COD≌△DFE,
∴DF=OC=3,EF=OD=1,
∴E点的坐标为(4,1),
故答案为(4,1).
七.平行线的判定(共1小题)
12.(2021春 奉贤区期末)如图,已知AE平分∠BAC交BC于点E,AF平分∠CAD交BC的延长线于点F,∠B=64°,∠EAF=58°,试判断AD与BC是否平行.
解:∵AE平分∠BAC,AF平分∠CAD(已知),
∴∠BAC=2∠1,∠CAD= 2∠2 ( 角平分线的定义 ).
又∵∠EAF=∠1+∠2=58°,
∴∠BAD=∠BAC+∠CAD
=2(∠1+∠2)
= 116 °(等式性质).
又∵∠B=64°(已知),
∴∠BAD+∠B= 180 °.
∴ AD ∥ BC ( 同旁内角互补,两直线平行 ).
【解答】解:∵AE平分∠BAC,AF平分∠CAD(已知),
∴∠BAC=2∠1,∠CAD=2∠2(角平分线的定义).
又∵∠EAF=∠1+∠2=58°,
∴∠BAD=∠BAC+∠CAD
=2(∠1+∠2)
=116°(等式性质).
又∵∠B=64°(已知),
∴∠BAD+∠B=180°.
∴AD∥BC(同旁内角互补,两直线平行).
故答案为:2∠2;角平分线的定义;116;180;AD;BC;同旁内角互补,两直线平行.
八.平行线的判定与性质(共1小题)
13.(2021春 静安区期末)如图,已知在△ABC中,FG∥EB,∠2=∠3,说明∠EDB+∠DBC=180°的理由.
解:∵FG∥EB( 已知 ),
∴ ∠1 = ∠2 ( 两直线平行,同位角相等 ).
∵∠2=∠3(已知),
∴ ∠1 = ∠3 ( 等量代换 ).
∴DE∥BC( 内错角相等,两直线平行 ),
∴∠EDB+∠DBC=180°( 两直线平行,同旁内角互补 ).
【解答】解:∵FG∥EB(已知),
∴∠1=∠2(两直线平行,同位角相等).
∵∠2=∠3(已知),
∴∠1=∠3(等量代换).
∴DE∥BC(内错角相等,两直线平行).
∴∠EDB+∠DBC=180°(两直线平行,同旁内角互补).
故答案为:已知;∠1;∠2;两直线平行,同位角相等;∠1;∠3;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补.
九.三角形内角和定理(共2小题)
14.(2021春 金山区期末)如图,在△ABC中,∠A=20°,∠B=60°,CD平分∠ACB交AB边于点D,求∠CDB的度数.
【解答】解:∵∠A=20°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=100°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=50°,
∴∠BDC=180°﹣∠B﹣∠BCD=70°.
15.(2021春 邗江区期末)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为 30 °,△AOB 是 .(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC 是 (填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
【解答】解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3)①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;
②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.
③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
一十.全等三角形的判定与性质(共18小题)
16.(2021春 奉贤区期末)如图,已知AD=BC,AE=BE,说明AC=BD的理由.
【解答】证明:∵AD=BC,AE=BE,
∴AD﹣AE=BC﹣BE,
即DE=CE,
在△ACE与△BDE中,
,
∴△ACE≌△BDE(SAS),
∴AC=BD.
17.(2021春 浦东新区期末)如图,在△ABC中,E是AD上的一点,EB=EC,∠ABE=∠ACE,请说明AD⊥BC.
解:因为EB=EC(已知),
所以∠EBC=∠ECB( 等边对等角 ).
又因为∠ABE=∠ACE(已知),
所以∠ABE+∠EBC=∠ACE+∠ECB( 等式性质 ).
即∠ABC=∠ACB.
所以AB=AC( 等角对等边 ).
在△ABE和△ACE中,
所以△ABE≌△ACE( SSS ).
得∠BAD=∠CAD( 全等三角形对应角相等 ).
所以AD⊥BC( 等腰三角形的三线合一 ).
【解答】解:因为EB=EC(已知),
所以∠EBC=∠ECB(等边对等角).
又因为∠ABE=∠ACE(已知),
所以∠ABE+∠EBC=∠ACE+∠ECB(等式性质).
即∠ABC=∠ACB.
所以AB=AC(等角对等边).
在△ABE和△ACE中,
所以△ABE≌△ACE(SSS),
得∠BAD=∠CAD(全等三角形对应角相等),
所以AD⊥BC(等腰三角形的三线合一).
故答案为:①等边对等角;②等式性质;③等角对等边;④公共边;⑤边、边、边(sss);⑥全等三角形对应角相等;⑦等腰三角形的三线合一.
18.(2021春 浦东新区期末)如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
【解答】解:∠B与∠C相等,
理由:∵∠FDC=∠FDE+∠EDC,
又∵∠FDC=∠B+∠BFD,
∴∠FDE+∠EDC=∠B+∠BFD,
又∵∠FDE=∠B,
∴∠BFD=∠EDC,
在△BFD和△CDE中
,
∴△BFD≌△CDE(SAS),
∴∠B=∠C.
19.(2021春 杨浦区期末)如图,已知△ABC与△BDE都是等边三角形,点D在边AC上,说明CE∥AB的理由.
解:因为△ABC是等边三角形(已知),
所以∠A=∠ABC=60°,AB=BC(等边三角形的意义).
因为△BDE是等边三角形(已知),
所以∠DBE=60°,BD=BE(等边三角形的意义).
所以∠ABC﹣∠DBC=∠DBE﹣∠DBC(等式性质),
得∠ABD= ∠CBE .
在△ABD与△CBE中,,
所以△ABD≌△CBE( SAS ).
所以∠A= ∠BCE ( 全等三角形的对应角相等 ).
又因为∠A=∠ABC,
所以∠ABC= ∠BCE (等量代换).
所以CE∥AB( 内错角相等,两直线平行 ).
【解答】解:因为△ABC是等边三角形(已知),
所以∠A=∠ABC=60°,AB=BC(等边三角形的意义).
因为△BDE是等边三角形(已知),
所以∠DBE=60°,BD=BE(等边三角形的意义).
所以∠ABC﹣∠DBC=∠DBE﹣∠DBC(等式性质),
得∠ABD=∠CBE.
在△ABD与△CBE中,,
所以△ABD≌△CBE(SAS).
所以∠A=∠BCE(全等三角形的对应角相等).
又因为∠A=∠ABC,
所以∠ABC=∠BCE(等量代换).
所以CE∥AB(内错角相等,两直线平行).
故答案为∠CBE,SAS,∠BCE,全等三角形的对应角相等;∠BCE,内错角相等,两直线平行.
20.(2021春 杨浦区期末)如图,已知△ADE≌△CBF,顶点A、D、E分别与顶点C、B、F对应,据此可以判断图中有哪几组直线互相平行?请说明理由.
【解答】解:可以判断AD∥BC,AB∥CD,DE∥BF三组直线平行,
理由如下:∵△ADE≌△CBF,
∴∠DAE=∠BCF,∠AED=∠CFB,AE=CF,DE=BF,
∴AD∥BC,∠CED=∠AFB,AE+EF=CF+EF,
∴ED∥BF,AF=CE,
在△CDE和△ABF中,
,
∴△CDE≌△ABF(SAS),
∴∠DCE=∠BAF,
∴AB∥CD,
∴AD∥BC,AB∥CD,DE∥BF.
21.(2021春 浦东新区期末)如图,在△ABC中,点D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.试说明AD=ED的理由.
解:因为CE∥AB(已知),
所以∠BAD= ∠E ( 两直线平行,内错角相等 ).
因为点D是边BC的中点,
所以 BD=CD ,
在△ABD和△ECD中,
,
所以△ABD≌△ECD( AAS ),
所以AD=ED( 全等三角形的对应边相等 ).
【解答】解:因为CE∥AB(已知),
所以∠BAD=∠E(两直线平行,内错角相等).
因为点D是边BC的中点,
所以BD=CD,
在△ABD和△ECD中,
所以△ABD≌△ECD(AAS),
所以AD=ED(全等三角形的对应边相等).
故答案为∠E,两直线平行,内错角相等;∠BAD=∠E,对顶角相等,BD=CD;AAS;全等三角形的对应边相等.
22.(2021春 黄浦区期末)如图,已知在△ABC中,∠ACB=90°,AC=BC,∠A的平分线AD交BC于点D,过点B作BE⊥AD于E.
(1)说明△ACD≌△BCF的理由;
(2)BE与AD的长度关系是 BE= ,请说明理由.
【解答】解:(1)∵BE⊥AD,
∴∠AEB=90°,
∵∠ACB=90°,
∴∠AEB=∠ACB,
∵∠ADC=∠BDE,
∴∠CAD=∠CBF,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(ASA).
(2)由(1)△ACD≌△BCF得:BF=AD,
∵AD平分∠BAF,
∴∠BAE=∠FAE,
在△BAE和△FAE中,
,
∴△BAE≌△FAE(ASA),
∴BE=EF,
∴BE=.
故答案为:BE=.
23.(2021春 黄浦区期末)如图在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.
(1)说明△ADE≌△BFE的理由;
(2)联结EG,那么EG与DF的位置关系是 EG⊥DF ,请说明理由.
【解答】解:(1)∵AD∥BC,
∴∠1=∠F,
∵E是AB的中点,
∴AE=BE,
在△ADE和△BFE中,
,
∴△ADE≌△BFE(AAS),
(2)如图,EG⊥DF,
∵∠1=∠F,∠1=∠2,
∴∠2=∠F,
∴DG=FG,
由(1)知:△ADE≌△BFE,
∴DE=EF,
∴EG⊥DF.
24.(2021春 嘉定区期末)如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
【解答】证明:法1:∵AB=AC,
∴∠B=∠C(等边对等角),
∵AD=AE,
∴∠ADE=∠AED(等边对等角),
又∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,
∴∠BAD=∠CAE(等量代换),
在△ABD和△ACE中,
,
∴△ABD≌△ACE(ASA),
∴BD=CE(全等三角形的对应边相等);
法2:过点A作AH⊥BC,垂足为点H,
∵AB=AC,AH⊥BC,
∴BH=CH(等腰三角形底边上的高与底边上的中线重合),
同理可证,DH=EH,
∴BH﹣DH=CH﹣EH,
∴BD=CE.
25.(2021春 嘉定区期末)如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AE=BE,AD与BE相交于点F.
(1)请说明△AEF≌△BEC的理由.
(2)如果AF=2BD,试说明AD平分∠BAC的理由.
【解答】解:(1)∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC+∠C=90°,
∴∠DAC=90°﹣∠C,
∴∠DAC=∠EBC,
在△AEF和△BEC中,
,
∴△AEF≌△BEC(AAS);
(2)由(1)知,AF=BC,
∵AF=2BD,
∴BC=2BD,
∴D是BC的中点,
∴BD=CD,
∵AD⊥BC,∠BAD=∠CAD=∠BAC,
∴AD平分∠BAC.
26.(2021春 静安区校级期末)如图,△ABC中,两条高BD和CE相交于H,已知AB=CH.试判断△BCD的形状并说明理由.
【解答】解:△BCD是等腰直角三角形,理由如下:
∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
∴∠A+∠ABD=90°,∠A+∠HCD=90°,
∴∠ABD=∠HCD,
∴在△ABD和△HCD中,
,
∴△ABD≌△HCD(AAS),
∴BD=CD,
∴△BCD是等腰直角三角形.
27.(2021春 浦东新区校级期末)如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
【解答】解:AB+BE=CD,理由如下:
∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴AB=DE,BD=CD,
∵DE+BE=BD,
∴AB+BE=CD.
28.(2021春 金山区期末)如图,已知△ACM是等边三角形,点E在边CM上,以CE为边作等边△CEF,联结AE并延长交CF的延长线于点N,联结MF并延长交AC的延长线于点B,联结BN.
(1)说明△ACE≌△MCF的理由;
(2)说明△CNB为等边三角形的理由.
【解答】证明:(1)△ACM和△CEF是等边三角形,
∴CA=CM,CE=CF,
∠ACM=∠ECF=60°,
在△ACE和△MCF中,
,
∴△ACE≌△MCF(SAS),
(2)∵△ACE≌△MCF(SAS),
∴∠CAE=∠CMF,
∵∠ACN=∠ACM+∠ECF=120°,∠MCB=180°﹣∠ACM=120°,
∴∠ACN=∠MCB,
在△ACN与△MCB中,
,
∴△ACN≌△MCB(ASA),
∴CN=CB,
∵∠BCN=180°﹣∠ACM﹣∠ECF=60°,
∴△CNB是等边三角形.
29.(2021 永嘉县校级模拟)如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,过点B作BE⊥AC,垂足为E,在线段BE上截取ED=EC,AD的延长线交BC于点P,联结DC.
(1)请说明AD=BC的理由;
(2)请说明BP=PC的理由.
【解答】解:(1)∵BE⊥AC,∠BAC=45°,
∴∠ABE=90°﹣45°=45°,
∴BE=AE,
在△BCE和△ADE中,
,
∴△BCE≌△ADE(SAS),
∴AD=BC.
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵BE⊥AC,BE=AE,EC=ED,
∴∠DCE=∠CDE=∠EBA=∠BAE=45°,
∴∠ABC﹣∠EBA=∠ACB﹣∠DCE,即∠DBC=∠DCB,
∴BD=CD,
∴PD为线段BC的垂直平分线,
∴BP=PC.
30.(2021春 松江区期末)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠EAF=∠BAD.
(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由;
(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.
【解答】解:(1)EF=BE+DF,
理由:延长EB至G,使BG=DF,连接AG,
∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,
∴∠ADC=∠ABG,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵∠EAF=∠BAD,
∴∠BAE+∠DAF=∠BAE+∠BAG=∠EAF,
即∠EAG=∠EAF,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=EF,
∴EF=BE+DF;
(2)(1)中结论不成立,EF=BE﹣FD,
在BE上截取BM=DF,连接AM,
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠ABC=∠ADF,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∵∠BAM+∠MAD=∠DAF+∠MAD,
∴∠BAD=∠MAF,
∵∠EAF=∠BAD,
∴∠EAF=∠MAF,
∴∠EAF=∠EAM,
在△AME和△AFE中,
,
∴△AME≌△AFE(SAS),
∴ME=EF,
∴ME=BE﹣BM=BE﹣DF,
∴EF=BE﹣FD.
31.(2021春 浦东新区期末)已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)求证:CF=CH;
(3)判断△CFH的形状并说明理由.
【解答】解:(1)证明:∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠DCE=60°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
∴∠BCE=ACD.
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS);
(2)∵△BCE≌△ACD,
∴∠CBE=∠CAD.
∵∠ACB+∠ACE+∠DCE=180°,
∴∠ACE=60°,
∴∠ACE=∠ACB.
在△ACH和△BCF中,
,
∴△ACH≌△BCF(ASA),
∴CH=CF;
(3)△CFH是等边三角形.
理由:连接FH.
∵∠ACE=60°,CH=CF,
∴△CFH是等边三角形.
32.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
【解答】解:(1)AD=CB,理由如下:
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,理由如下:
∵AD=CB,BE=AD,
∴BC=BE,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
33.(2021春 奉贤区期末)如图,在△ABC中,已知D是BC边的中点,过点D的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,交AC的延长线于点E,联结EG.
(1)说明BG与CF相等的理由.
(2)说明∠BGD与∠DGE相等的理由.
【解答】解 (1)∵D为BC中点,
∴BD=DC(中点的定义),
∵BG∥FC(已知),
∴∠GBD=∠DCF(两直线平行,内错角相等),
在△BDG和△CDF中,
,
∴△BDG≌△CDF(ASA),
∴BG=CF(全等三角形对应边相等);
(2)∵DE为线段GF的中垂线(中垂线定义),
∴EF=EG(中垂线性质),
∴∠DFE=∠DGE(等边对等角),)
∵∠DFE=∠BGD(全等三角形对应角相等),
∴∠BGD=∠DGE(等量代换).
一.平方根(共1小题)
1.(2021春 浦东新区期末)一个正数x的两个不同的平方根分别是2a﹣1和﹣a+2.
(1)求a和x的值;
(2)求3x+2a的平方根.
二.实数的运算(共6小题)
2.(2021春 浦东新区期末)计算:
.
3.(2021春 嘉定区期末)用幂的运算性质计算:(结果表示为含幂的形式).
4.(2021春 奉贤区期末)计算:.
5.(2021春 奉贤区期末)利用幂的运算性质计算:﹣×÷(结果用幂的形式表示).
6.(2021春 杨浦区期末)用幂的运算性质计算:(结果表示为含幂的形式).
7.(2021春 黄浦区期末)利用幂的运算性质计算:.
三.分数指数幂(共1小题)
8.(2021春 静安区期末)用幂的性质计算:(5﹣17) (5+17).
四.二次根式的乘除法(共1小题)
9.(2021春 黄浦区期末)计算:.
五.二次根式的混合运算(共1小题)
10.(2021春 奉贤区期末)计算:(3﹣2)×+(﹣)2.
六.一次函数图象上点的坐标特征(共1小题)
11.(2021春 杨浦区期末)如图,在平面直角坐标系中,点A(﹣2,﹣3),点A关于x轴的对称点记作点B,将点B向右平移2个单位得点C.
(1)分别写出点B、C的坐标:B( )、C( );
(2)点D在x轴的正半轴上,点E在直线y=1上,如果△CDE是以CD为腰的等腰直角三角形,那么点E的坐标是 .
七.平行线的判定(共1小题)
12.(2021春 奉贤区期末)如图,已知AE平分∠BAC交BC于点E,AF平分∠CAD交BC的延长线于点F,∠B=64°,∠EAF=58°,试判断AD与BC是否平行.
解:∵AE平分∠BAC,AF平分∠CAD(已知),
∴∠BAC=2∠1,∠CAD= ( ).
又∵∠EAF=∠1+∠2=58°,
∴∠BAD=∠BAC+∠CAD
=2(∠1+∠2)
= °(等式性质).
又∵∠B=64°(已知),
∴∠BAD+∠B= °.
∴ ∥ ( ).
八.平行线的判定与性质(共1小题)
13.(2021春 静安区期末)如图,已知在△ABC中,FG∥EB,∠2=∠3,说明∠EDB+∠DBC=180°的理由.
解:∵FG∥EB( ),
∴ = ( ).
∵∠2=∠3(已知),
∴ = ( ).
∴DE∥BC( ),
∴∠EDB+∠DBC=180°( ).
九.三角形内角和定理(共2小题)
14.(2021春 金山区期末)如图,在△ABC中,∠A=20°,∠B=60°,CD平分∠ACB交AB边于点D,求∠CDB的度数.
15.(2021春 邗江区期末)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为 °,△AOB .(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC (填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
一十.全等三角形的判定与性质(共18小题)
16.(2021春 奉贤区期末)如图,已知AD=BC,AE=BE,说明AC=BD的理由.
17.(2021春 浦东新区期末)如图,在△ABC中,E是AD上的一点,EB=EC,∠ABE=∠ACE,请说明AD⊥BC.
解:因为EB=EC(已知),
所以∠EBC=∠ECB( ).
又因为∠ABE=∠ACE(已知),
所以∠ABE+∠EBC=∠ACE+∠ECB( ).
即∠ABC=∠ACB.
所以AB=AC( ).
在△ABE和△ACE中,
所以△ABE≌△ACE( ).
得∠BAD=∠CAD( ).
所以AD⊥BC( ).
18.(2021春 浦东新区期末)如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
19.(2021春 杨浦区期末)如图,已知△ABC与△BDE都是等边三角形,点D在边AC上,说明CE∥AB的理由.
解:因为△ABC是等边三角形(已知),
所以∠A=∠ABC=60°,AB=BC(等边三角形的意义).
因为△BDE是等边三角形(已知),
所以∠DBE=60°,BD=BE(等边三角形的意义).
所以∠ABC﹣∠DBC=∠DBE﹣∠DBC(等式性质),
得∠ABD= .
在△ABD与△CBE中,,
所以△ABD≌△CBE( ).
所以∠A= ( ).
又因为∠A=∠ABC,
所以∠ABC= (等量代换).
所以CE∥AB( ).
20.(2021春 杨浦区期末)如图,已知△ADE≌△CBF,顶点A、D、E分别与顶点C、B、F对应,据此可以判断图中有哪几组直线互相平行?请说明理由.
21.(2021春 浦东新区期末)如图,在△ABC中,点D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.试说明AD=ED的理由.
解:因为CE∥AB(已知),
所以∠BAD= ( ).
因为点D是边BC的中点,
所以 ,
在△ABD和△ECD中,
,
所以△ABD≌△ECD( ),
所以AD=ED( ).
22.(2021春 黄浦区期末)如图,已知在△ABC中,∠ACB=90°,AC=BC,∠A的平分线AD交BC于点D,过点B作BE⊥AD于E.
(1)说明△ACD≌△BCF的理由;
(2)BE与AD的长度关系是 ,请说明理由.
23.(2021春 黄浦区期末)如图在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.
(1)说明△ADE≌△BFE的理由;
(2)联结EG,那么EG与DF的位置关系是 ,请说明理由.
24.(2021春 嘉定区期末)如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
25.(2021春 嘉定区期末)如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AE=BE,AD与BE相交于点F.
(1)请说明△AEF≌△BEC的理由.
(2)如果AF=2BD,试说明AD平分∠BAC的理由.
26.(2021春 静安区校级期末)如图,△ABC中,两条高BD和CE相交于H,已知AB=CH.试判断△BCD的形状并说明理由.
27.(2021春 浦东新区校级期末)如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
28.(2021春 金山区期末)如图,已知△ACM是等边三角形,点E在边CM上,以CE为边作等边△CEF,联结AE并延长交CF的延长线于点N,联结MF并延长交AC的延长线于点B,联结BN.
(1)说明△ACE≌△MCF的理由;
(2)说明△CNB为等边三角形的理由.
29.(2021 永嘉县校级模拟)如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,过点B作BE⊥AC,垂足为E,在线段BE上截取ED=EC,AD的延长线交BC于点P,联结DC.
(1)请说明AD=BC的理由;
(2)请说明BP=PC的理由.
30.(2021春 松江区期末)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠EAF=∠BAD.
(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由;
(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.
31.(2021春 浦东新区期末)已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)求证:CF=CH;
(3)判断△CFH的形状并说明理由.
32.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
33.(2021春 奉贤区期末)如图,在△ABC中,已知D是BC边的中点,过点D的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,交AC的延长线于点E,联结EG.
(1)说明BG与CF相等的理由.
(2)说明∠BGD与∠DGE相等的理由.
参考答案与试题解析
一.平方根(共1小题)
1.(2021春 浦东新区期末)一个正数x的两个不同的平方根分别是2a﹣1和﹣a+2.
(1)求a和x的值;
(2)求3x+2a的平方根.
【解答】解:(1)∵一个正数的两个平方根互为相反数,
∴2a﹣1+(﹣a+2)=0,
解得a=﹣1,
∴x=(2a﹣1)2=(﹣3)2=9.
(2)∵3x+2a=3×9﹣2=25,
∴25的平方根为±5.
二.实数的运算(共6小题)
2.(2021春 浦东新区期末)计算:
.
【解答】解:原式=3﹣4+3﹣﹣1=1﹣.
3.(2021春 嘉定区期末)用幂的运算性质计算:(结果表示为含幂的形式).
【解答】解:原式=4×8÷32
=2×2÷2
=2
=2.
4.(2021春 奉贤区期末)计算:.
【解答】解:原式=2+﹣+1
=2﹣3﹣6+1
=﹣6.
5.(2021春 奉贤区期末)利用幂的运算性质计算:﹣×÷(结果用幂的形式表示).
【解答】解:原式=﹣×(﹣)÷
=×÷
=
=.
6.(2021春 杨浦区期末)用幂的运算性质计算:(结果表示为含幂的形式).
【解答】解:原式=3×9÷81
=3×3÷3
=3
=3.
7.(2021春 黄浦区期末)利用幂的运算性质计算:.
【解答】解:原式=2×2×2×
=2×2
=2×2
=2.
三.分数指数幂(共1小题)
8.(2021春 静安区期末)用幂的性质计算:(5﹣17) (5+17).
【解答】解:原式=[(5﹣)(5+)]
=(25﹣17)
=8
=
=2
四.二次根式的乘除法(共1小题)
9.(2021春 黄浦区期末)计算:.
【解答】解:原式=××2×
=1.
五.二次根式的混合运算(共1小题)
10.(2021春 奉贤区期末)计算:(3﹣2)×+(﹣)2.
【解答】解:原式=3﹣6+(2+3﹣2)
=3﹣6+5﹣2
=﹣1.
六.一次函数图象上点的坐标特征(共1小题)
11.(2021春 杨浦区期末)如图,在平面直角坐标系中,点A(﹣2,﹣3),点A关于x轴的对称点记作点B,将点B向右平移2个单位得点C.
(1)分别写出点B、C的坐标:B( ﹣2,3 )、C( 0,3 );
(2)点D在x轴的正半轴上,点E在直线y=1上,如果△CDE是以CD为腰的等腰直角三角形,那么点E的坐标是 (﹣1,1) .
【解答】解:(1)∵将点A(﹣2,﹣3)关于x轴的对称点B的坐标为(﹣2,3),
将点B向右平移2个单位得点C,
∴C(0,3),
故答案为﹣2,3;0,3;
(2)作EF⊥x轴于F,
由题意可知,△COD≌△DFE,
∴DF=OC=3,EF=OD=1,
∴E点的坐标为(4,1),
故答案为(4,1).
七.平行线的判定(共1小题)
12.(2021春 奉贤区期末)如图,已知AE平分∠BAC交BC于点E,AF平分∠CAD交BC的延长线于点F,∠B=64°,∠EAF=58°,试判断AD与BC是否平行.
解:∵AE平分∠BAC,AF平分∠CAD(已知),
∴∠BAC=2∠1,∠CAD= 2∠2 ( 角平分线的定义 ).
又∵∠EAF=∠1+∠2=58°,
∴∠BAD=∠BAC+∠CAD
=2(∠1+∠2)
= 116 °(等式性质).
又∵∠B=64°(已知),
∴∠BAD+∠B= 180 °.
∴ AD ∥ BC ( 同旁内角互补,两直线平行 ).
【解答】解:∵AE平分∠BAC,AF平分∠CAD(已知),
∴∠BAC=2∠1,∠CAD=2∠2(角平分线的定义).
又∵∠EAF=∠1+∠2=58°,
∴∠BAD=∠BAC+∠CAD
=2(∠1+∠2)
=116°(等式性质).
又∵∠B=64°(已知),
∴∠BAD+∠B=180°.
∴AD∥BC(同旁内角互补,两直线平行).
故答案为:2∠2;角平分线的定义;116;180;AD;BC;同旁内角互补,两直线平行.
八.平行线的判定与性质(共1小题)
13.(2021春 静安区期末)如图,已知在△ABC中,FG∥EB,∠2=∠3,说明∠EDB+∠DBC=180°的理由.
解:∵FG∥EB( 已知 ),
∴ ∠1 = ∠2 ( 两直线平行,同位角相等 ).
∵∠2=∠3(已知),
∴ ∠1 = ∠3 ( 等量代换 ).
∴DE∥BC( 内错角相等,两直线平行 ),
∴∠EDB+∠DBC=180°( 两直线平行,同旁内角互补 ).
【解答】解:∵FG∥EB(已知),
∴∠1=∠2(两直线平行,同位角相等).
∵∠2=∠3(已知),
∴∠1=∠3(等量代换).
∴DE∥BC(内错角相等,两直线平行).
∴∠EDB+∠DBC=180°(两直线平行,同旁内角互补).
故答案为:已知;∠1;∠2;两直线平行,同位角相等;∠1;∠3;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补.
九.三角形内角和定理(共2小题)
14.(2021春 金山区期末)如图,在△ABC中,∠A=20°,∠B=60°,CD平分∠ACB交AB边于点D,求∠CDB的度数.
【解答】解:∵∠A=20°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=100°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=50°,
∴∠BDC=180°﹣∠B﹣∠BCD=70°.
15.(2021春 邗江区期末)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为 30 °,△AOB 是 .(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC 是 (填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
【解答】解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3)①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;
②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.
③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
一十.全等三角形的判定与性质(共18小题)
16.(2021春 奉贤区期末)如图,已知AD=BC,AE=BE,说明AC=BD的理由.
【解答】证明:∵AD=BC,AE=BE,
∴AD﹣AE=BC﹣BE,
即DE=CE,
在△ACE与△BDE中,
,
∴△ACE≌△BDE(SAS),
∴AC=BD.
17.(2021春 浦东新区期末)如图,在△ABC中,E是AD上的一点,EB=EC,∠ABE=∠ACE,请说明AD⊥BC.
解:因为EB=EC(已知),
所以∠EBC=∠ECB( 等边对等角 ).
又因为∠ABE=∠ACE(已知),
所以∠ABE+∠EBC=∠ACE+∠ECB( 等式性质 ).
即∠ABC=∠ACB.
所以AB=AC( 等角对等边 ).
在△ABE和△ACE中,
所以△ABE≌△ACE( SSS ).
得∠BAD=∠CAD( 全等三角形对应角相等 ).
所以AD⊥BC( 等腰三角形的三线合一 ).
【解答】解:因为EB=EC(已知),
所以∠EBC=∠ECB(等边对等角).
又因为∠ABE=∠ACE(已知),
所以∠ABE+∠EBC=∠ACE+∠ECB(等式性质).
即∠ABC=∠ACB.
所以AB=AC(等角对等边).
在△ABE和△ACE中,
所以△ABE≌△ACE(SSS),
得∠BAD=∠CAD(全等三角形对应角相等),
所以AD⊥BC(等腰三角形的三线合一).
故答案为:①等边对等角;②等式性质;③等角对等边;④公共边;⑤边、边、边(sss);⑥全等三角形对应角相等;⑦等腰三角形的三线合一.
18.(2021春 浦东新区期末)如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
【解答】解:∠B与∠C相等,
理由:∵∠FDC=∠FDE+∠EDC,
又∵∠FDC=∠B+∠BFD,
∴∠FDE+∠EDC=∠B+∠BFD,
又∵∠FDE=∠B,
∴∠BFD=∠EDC,
在△BFD和△CDE中
,
∴△BFD≌△CDE(SAS),
∴∠B=∠C.
19.(2021春 杨浦区期末)如图,已知△ABC与△BDE都是等边三角形,点D在边AC上,说明CE∥AB的理由.
解:因为△ABC是等边三角形(已知),
所以∠A=∠ABC=60°,AB=BC(等边三角形的意义).
因为△BDE是等边三角形(已知),
所以∠DBE=60°,BD=BE(等边三角形的意义).
所以∠ABC﹣∠DBC=∠DBE﹣∠DBC(等式性质),
得∠ABD= ∠CBE .
在△ABD与△CBE中,,
所以△ABD≌△CBE( SAS ).
所以∠A= ∠BCE ( 全等三角形的对应角相等 ).
又因为∠A=∠ABC,
所以∠ABC= ∠BCE (等量代换).
所以CE∥AB( 内错角相等,两直线平行 ).
【解答】解:因为△ABC是等边三角形(已知),
所以∠A=∠ABC=60°,AB=BC(等边三角形的意义).
因为△BDE是等边三角形(已知),
所以∠DBE=60°,BD=BE(等边三角形的意义).
所以∠ABC﹣∠DBC=∠DBE﹣∠DBC(等式性质),
得∠ABD=∠CBE.
在△ABD与△CBE中,,
所以△ABD≌△CBE(SAS).
所以∠A=∠BCE(全等三角形的对应角相等).
又因为∠A=∠ABC,
所以∠ABC=∠BCE(等量代换).
所以CE∥AB(内错角相等,两直线平行).
故答案为∠CBE,SAS,∠BCE,全等三角形的对应角相等;∠BCE,内错角相等,两直线平行.
20.(2021春 杨浦区期末)如图,已知△ADE≌△CBF,顶点A、D、E分别与顶点C、B、F对应,据此可以判断图中有哪几组直线互相平行?请说明理由.
【解答】解:可以判断AD∥BC,AB∥CD,DE∥BF三组直线平行,
理由如下:∵△ADE≌△CBF,
∴∠DAE=∠BCF,∠AED=∠CFB,AE=CF,DE=BF,
∴AD∥BC,∠CED=∠AFB,AE+EF=CF+EF,
∴ED∥BF,AF=CE,
在△CDE和△ABF中,
,
∴△CDE≌△ABF(SAS),
∴∠DCE=∠BAF,
∴AB∥CD,
∴AD∥BC,AB∥CD,DE∥BF.
21.(2021春 浦东新区期末)如图,在△ABC中,点D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.试说明AD=ED的理由.
解:因为CE∥AB(已知),
所以∠BAD= ∠E ( 两直线平行,内错角相等 ).
因为点D是边BC的中点,
所以 BD=CD ,
在△ABD和△ECD中,
,
所以△ABD≌△ECD( AAS ),
所以AD=ED( 全等三角形的对应边相等 ).
【解答】解:因为CE∥AB(已知),
所以∠BAD=∠E(两直线平行,内错角相等).
因为点D是边BC的中点,
所以BD=CD,
在△ABD和△ECD中,
所以△ABD≌△ECD(AAS),
所以AD=ED(全等三角形的对应边相等).
故答案为∠E,两直线平行,内错角相等;∠BAD=∠E,对顶角相等,BD=CD;AAS;全等三角形的对应边相等.
22.(2021春 黄浦区期末)如图,已知在△ABC中,∠ACB=90°,AC=BC,∠A的平分线AD交BC于点D,过点B作BE⊥AD于E.
(1)说明△ACD≌△BCF的理由;
(2)BE与AD的长度关系是 BE= ,请说明理由.
【解答】解:(1)∵BE⊥AD,
∴∠AEB=90°,
∵∠ACB=90°,
∴∠AEB=∠ACB,
∵∠ADC=∠BDE,
∴∠CAD=∠CBF,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(ASA).
(2)由(1)△ACD≌△BCF得:BF=AD,
∵AD平分∠BAF,
∴∠BAE=∠FAE,
在△BAE和△FAE中,
,
∴△BAE≌△FAE(ASA),
∴BE=EF,
∴BE=.
故答案为:BE=.
23.(2021春 黄浦区期末)如图在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.
(1)说明△ADE≌△BFE的理由;
(2)联结EG,那么EG与DF的位置关系是 EG⊥DF ,请说明理由.
【解答】解:(1)∵AD∥BC,
∴∠1=∠F,
∵E是AB的中点,
∴AE=BE,
在△ADE和△BFE中,
,
∴△ADE≌△BFE(AAS),
(2)如图,EG⊥DF,
∵∠1=∠F,∠1=∠2,
∴∠2=∠F,
∴DG=FG,
由(1)知:△ADE≌△BFE,
∴DE=EF,
∴EG⊥DF.
24.(2021春 嘉定区期末)如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
【解答】证明:法1:∵AB=AC,
∴∠B=∠C(等边对等角),
∵AD=AE,
∴∠ADE=∠AED(等边对等角),
又∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,
∴∠BAD=∠CAE(等量代换),
在△ABD和△ACE中,
,
∴△ABD≌△ACE(ASA),
∴BD=CE(全等三角形的对应边相等);
法2:过点A作AH⊥BC,垂足为点H,
∵AB=AC,AH⊥BC,
∴BH=CH(等腰三角形底边上的高与底边上的中线重合),
同理可证,DH=EH,
∴BH﹣DH=CH﹣EH,
∴BD=CE.
25.(2021春 嘉定区期末)如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AE=BE,AD与BE相交于点F.
(1)请说明△AEF≌△BEC的理由.
(2)如果AF=2BD,试说明AD平分∠BAC的理由.
【解答】解:(1)∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC+∠C=90°,
∴∠DAC=90°﹣∠C,
∴∠DAC=∠EBC,
在△AEF和△BEC中,
,
∴△AEF≌△BEC(AAS);
(2)由(1)知,AF=BC,
∵AF=2BD,
∴BC=2BD,
∴D是BC的中点,
∴BD=CD,
∵AD⊥BC,∠BAD=∠CAD=∠BAC,
∴AD平分∠BAC.
26.(2021春 静安区校级期末)如图,△ABC中,两条高BD和CE相交于H,已知AB=CH.试判断△BCD的形状并说明理由.
【解答】解:△BCD是等腰直角三角形,理由如下:
∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
∴∠A+∠ABD=90°,∠A+∠HCD=90°,
∴∠ABD=∠HCD,
∴在△ABD和△HCD中,
,
∴△ABD≌△HCD(AAS),
∴BD=CD,
∴△BCD是等腰直角三角形.
27.(2021春 浦东新区校级期末)如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
【解答】解:AB+BE=CD,理由如下:
∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴AB=DE,BD=CD,
∵DE+BE=BD,
∴AB+BE=CD.
28.(2021春 金山区期末)如图,已知△ACM是等边三角形,点E在边CM上,以CE为边作等边△CEF,联结AE并延长交CF的延长线于点N,联结MF并延长交AC的延长线于点B,联结BN.
(1)说明△ACE≌△MCF的理由;
(2)说明△CNB为等边三角形的理由.
【解答】证明:(1)△ACM和△CEF是等边三角形,
∴CA=CM,CE=CF,
∠ACM=∠ECF=60°,
在△ACE和△MCF中,
,
∴△ACE≌△MCF(SAS),
(2)∵△ACE≌△MCF(SAS),
∴∠CAE=∠CMF,
∵∠ACN=∠ACM+∠ECF=120°,∠MCB=180°﹣∠ACM=120°,
∴∠ACN=∠MCB,
在△ACN与△MCB中,
,
∴△ACN≌△MCB(ASA),
∴CN=CB,
∵∠BCN=180°﹣∠ACM﹣∠ECF=60°,
∴△CNB是等边三角形.
29.(2021 永嘉县校级模拟)如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,过点B作BE⊥AC,垂足为E,在线段BE上截取ED=EC,AD的延长线交BC于点P,联结DC.
(1)请说明AD=BC的理由;
(2)请说明BP=PC的理由.
【解答】解:(1)∵BE⊥AC,∠BAC=45°,
∴∠ABE=90°﹣45°=45°,
∴BE=AE,
在△BCE和△ADE中,
,
∴△BCE≌△ADE(SAS),
∴AD=BC.
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵BE⊥AC,BE=AE,EC=ED,
∴∠DCE=∠CDE=∠EBA=∠BAE=45°,
∴∠ABC﹣∠EBA=∠ACB﹣∠DCE,即∠DBC=∠DCB,
∴BD=CD,
∴PD为线段BC的垂直平分线,
∴BP=PC.
30.(2021春 松江区期末)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠EAF=∠BAD.
(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由;
(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.
【解答】解:(1)EF=BE+DF,
理由:延长EB至G,使BG=DF,连接AG,
∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,
∴∠ADC=∠ABG,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵∠EAF=∠BAD,
∴∠BAE+∠DAF=∠BAE+∠BAG=∠EAF,
即∠EAG=∠EAF,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=EF,
∴EF=BE+DF;
(2)(1)中结论不成立,EF=BE﹣FD,
在BE上截取BM=DF,连接AM,
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠ABC=∠ADF,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∵∠BAM+∠MAD=∠DAF+∠MAD,
∴∠BAD=∠MAF,
∵∠EAF=∠BAD,
∴∠EAF=∠MAF,
∴∠EAF=∠EAM,
在△AME和△AFE中,
,
∴△AME≌△AFE(SAS),
∴ME=EF,
∴ME=BE﹣BM=BE﹣DF,
∴EF=BE﹣FD.
31.(2021春 浦东新区期末)已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)求证:CF=CH;
(3)判断△CFH的形状并说明理由.
【解答】解:(1)证明:∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠DCE=60°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
∴∠BCE=ACD.
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS);
(2)∵△BCE≌△ACD,
∴∠CBE=∠CAD.
∵∠ACB+∠ACE+∠DCE=180°,
∴∠ACE=60°,
∴∠ACE=∠ACB.
在△ACH和△BCF中,
,
∴△ACH≌△BCF(ASA),
∴CH=CF;
(3)△CFH是等边三角形.
理由:连接FH.
∵∠ACE=60°,CH=CF,
∴△CFH是等边三角形.
32.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
【解答】解:(1)AD=CB,理由如下:
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,理由如下:
∵AD=CB,BE=AD,
∴BC=BE,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
33.(2021春 奉贤区期末)如图,在△ABC中,已知D是BC边的中点,过点D的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,交AC的延长线于点E,联结EG.
(1)说明BG与CF相等的理由.
(2)说明∠BGD与∠DGE相等的理由.
【解答】解 (1)∵D为BC中点,
∴BD=DC(中点的定义),
∵BG∥FC(已知),
∴∠GBD=∠DCF(两直线平行,内错角相等),
在△BDG和△CDF中,
,
∴△BDG≌△CDF(ASA),
∴BG=CF(全等三角形对应边相等);
(2)∵DE为线段GF的中垂线(中垂线定义),
∴EF=EG(中垂线性质),
∴∠DFE=∠DGE(等边对等角),)
∵∠DFE=∠BGD(全等三角形对应角相等),
∴∠BGD=∠DGE(等量代换).
同课章节目录
