11解答题(基础题)2021年春上海市各区七年级(下)期末数学知识点分类汇编(含解析)
文档属性
| 名称 | 11解答题(基础题)2021年春上海市各区七年级(下)期末数学知识点分类汇编(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 370.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 23:07:50 | ||
图片预览



文档简介
11解答题(基础题)
五.一次函数图象上点的坐标特征(共1小题)
32.(2021春 金山区期末)如图,已知在平面直角坐标系xOy中,点A(﹣4,0),点B(2n﹣10,m+2),当点A向右平移m(m>0)个单位,再向上平移n(n>0)个单位时,可与点B重合.
(1)求点B的坐标;
(2)将点B向右平移3个单位后得到的点记为点C,点C恰好在直线x=b上,点D在直线x=b上,当△BCD是等腰三角形时,求点D的坐标.
六.平行线的性质(共3小题)
33.(2021春 浦东新区期末)如图,∠ABE=80°,BF是∠ABE的平分线,且BF∥CD,求∠C的度数.
34.(2021春 静安区校级期末)已知AB∥CD,且CD平分∠FCB,∠CEB=90°,∠CBE=40°,求∠EBA的度数.
35.(2021春 松江区期末)如图,已知在△ABC中,点D在边AC上,DA=DB,过点D作DE∥AB交边BC于点E,请说明∠BDE=∠CDE的理由.
七.平行线的判定与性质(共7小题)
36.(2021春 嘉定区期末)如图,已知AD⊥BC,FG⊥BC,垂足分别为点D、G,∠1=∠2,试说明DE∥AC的理由.
解:因为AD⊥BC,FG⊥BC(已知),
所以∠ADC=90°,∠FGC=90°( ).
所以∠ADC=∠FGC(等量代换).
所以AD∥FG( ).
所以∠1=∠CAD( ),
因为∠1=∠2(已知).
所以∠2=∠CAD( ).
所以DE∥AC( ).
37.(2021春 金山区期末)已知:如图,AB∥CD,AD和BC交于点O,E为OC上一点,F为CD上一点,且∠CEF+∠BOD=180°.求证:∠EFC=∠A.
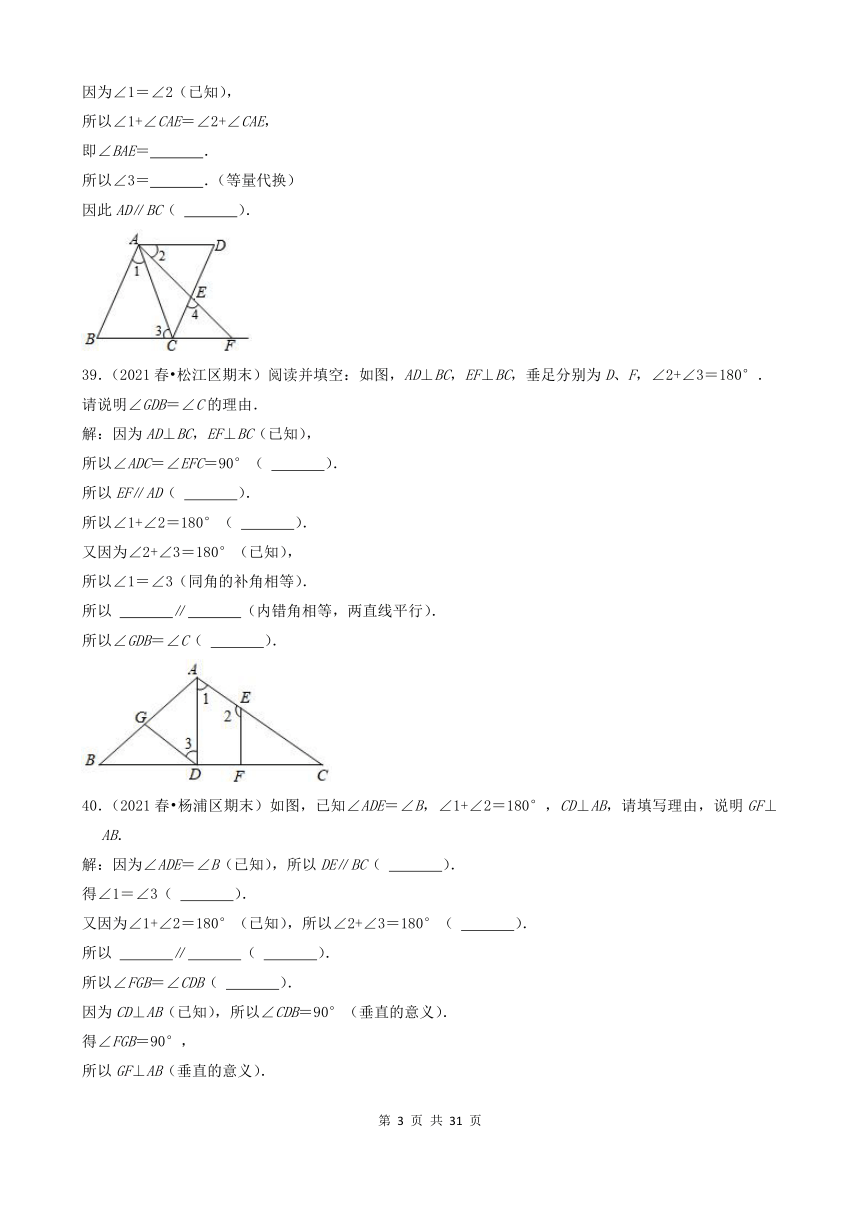
38.(2021春 静安区校级期末)如图,已知AB∥CD,∠1=∠2,∠3=∠4,请说明AD∥BC的理由.
解:因为AB∥CD(已知),
所以∠4=∠BAE( ),
因为∠3=∠4(已知),
所以∠3=∠BAE( ),
因为∠1=∠2(已知),
所以∠1+∠CAE=∠2+∠CAE,
即∠BAE= .
所以∠3= .(等量代换)
因此AD∥BC( ).
39.(2021春 松江区期末)阅读并填空:如图,AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
请说明∠GDB=∠C的理由.
解:因为AD⊥BC,EF⊥BC(已知),
所以∠ADC=∠EFC=90°( ).
所以EF∥AD( ).
所以∠1+∠2=180°( ).
又因为∠2+∠3=180°(已知),
所以∠1=∠3(同角的补角相等).
所以 ∥ (内错角相等,两直线平行).
所以∠GDB=∠C( ).
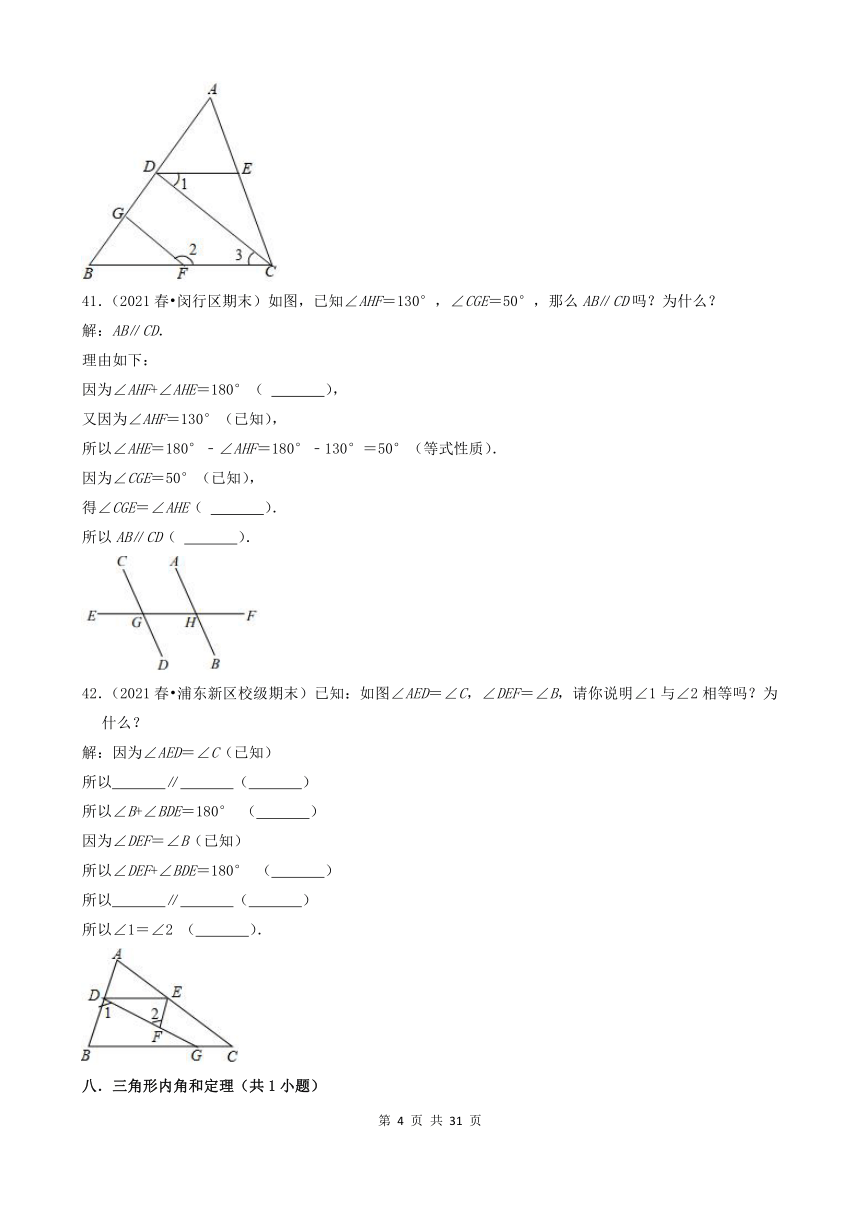
40.(2021春 杨浦区期末)如图,已知∠ADE=∠B,∠1+∠2=180°,CD⊥AB,请填写理由,说明GF⊥AB.
解:因为∠ADE=∠B(已知),所以DE∥BC( ).
得∠1=∠3( ).
又因为∠1+∠2=180°(已知),所以∠2+∠3=180°( ).
所以 ∥ ( ).
所以∠FGB=∠CDB( ).
因为CD⊥AB(已知),所以∠CDB=90°(垂直的意义).
得∠FGB=90°,
所以GF⊥AB(垂直的意义).
41.(2021春 闵行区期末)如图,已知∠AHF=130°,∠CGE=50°,那么AB∥CD吗?为什么?
解:AB∥CD.
理由如下:
因为∠AHF+∠AHE=180°( ),
又因为∠AHF=130°(已知),
所以∠AHE=180°﹣∠AHF=180°﹣130°=50°(等式性质).
因为∠CGE=50°(已知),
得∠CGE=∠AHE( ).
所以AB∥CD( ).
42.(2021春 浦东新区校级期末)已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ ( )
所以∠B+∠BDE=180° ( )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° ( )
所以 ∥ ( )
所以∠1=∠2 ( ).
八.三角形内角和定理(共1小题)
43.(2021春 静安区校级期末)如图,△ABC中,已知∠B=60°,∠ACD:∠A=5:2,求∠A的度数.
九.三角形的外角性质(共1小题)
44.(2021春 静安区校级期末)△ABC中,∠A、∠B、∠C的外角的度数之比是2:3:4,求∠A的度数.
一十.全等三角形的判定与性质(共10小题)
45.(2021春 黄浦区期末)如图,点A、B、C、D在一条直线上如果AC=BD,BE=CF,且BE∥CF,那么AE∥DF.为什么?
解:∵BE∥CF(已知),
∴∠EBC=∠FCB( ).
∵∠EBC+∠EBA=180°,∠FCB+∠FCD=180°(平角的意义),
∴∠EBA=∠FCD( ).
∵AC=BD(已知),
∴AC﹣BC=BD﹣BC(等式性质),
即 .(完成以下说理过程)
46.(2021春 静安区校级期末)已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.若AB=5,求AD的长.
47.(2021春 静安区校级期末)如图,在等边三角形ABC中,D、E分别是边AB、AC上的动点且AD=CE,连接DC、BE,记交点为F,试问DC、BE所成的∠BFC的大小有无变化?说明理由.
48.(2021春 静安区校级期末)填空并续写解题过程:
如图,已知AB=AC,∠1=∠2=∠3,BE=EF,说明BC=FC的理由.
解:因为AB=AC,∠1=∠2,
所以 ⊥ (等腰三角形三线合一),
所以∠ADC=90°(垂直的意义).
因为∠ADC+∠2+∠ACD=180°,∠BEC+∠3+∠BCE=180°( ),
所以∠ADC+∠2+∠ACD=∠BEC+∠3+∠BCE.
又因为∠2=∠3(已知),
所以∠BEC=∠ =90°(等式性质).
请续写解题过程,说明BC=FC的理由.
49.(2021春 金山区期末)阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,说明BD=CE的理由.
解:因为AB=AC,
所以 ;(等边对等角)
因为 ,(已知)
所以∠AED=∠ADE;(等边对等角)
因为∠AED=∠EAC+∠C,
∠ADE=∠BAD+∠B,( )
所以∠BAD=∠EAC;(等式性质)
在△ABD与△ACE中,
所以△ABD≌△ACE(A.S.A)
所以 .(全等三角形的对应边相等)
50.(2021春 闵行区期末)如图,△ABC中,AD⊥BC,垂足为点D,CE⊥AB,垂足为点E,AD=DC,CE和AD交于点F,联结BF,试说明∠FBD=45°.
51.(2021春 闵行区期末)如图,已知在等腰△ABC中AB=AC,点D,点E和点F分别是BC,AB和AC边上的点,且BE=DC,∠B=∠EDF,试说明DE=DF.
52.(2021春 浦东新区校级期末)如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
(1)试说明Rt△ABF≌Rt△DCE的理由;
(2)试说明OE=OF的理由.
53.(2021春 浦东新区校级期末)如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
54.(2021春 浦东新区校级期末)如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=44°,求∠BDE的度数.
一十一.等腰三角形的性质(共1小题)
55.(2021春 闵行区期末)已知在等腰△ABC中AB=AC,∠B=2∠A,求∠B的度数.
一十二.等腰三角形的判定(共1小题)
56.(2021春 松江区期末)如图,已知在△ABC中,AB=AC=BD,∠ADE=∠B,请说明△ADE是等腰三角形的理由.
一十三.关于原点对称的点的坐标(共3小题)
57.(2021春 静安区校级期末)已知点A的坐标为(﹣3,2),设点A关于x轴对称的点为点B,点A关于原点的对称点为点C,过点C作y轴的平行线交x轴于点D,
(1)点B的坐标是 ,点C的坐标是 .
(2)已知在线段BC上存在一点E,恰好能使△ABE≌△DEC,那么此时点E的坐标是 .
58.(2021春 静安区校级期末)如图,在直角坐标平面内,已知点A的坐标是(0,4).
(1)图中B点的坐标是 .
(2)点B关于原点对称的点C的坐标是 ;点A关于x轴对称的点D的坐标是 .
(3)△ABC的面积是 .
(4)如果点E在x轴上,且S△ADE=S△ABC,那么点E的坐标是 .
59.(2021春 浦东新区校级期末)如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是 ;
(2)点B关于原点对称的点C的坐标是 ;点A关于y轴对称的点D的坐标是 ;
(3)四边形ABDC的面积是 ;
(4)在y轴上找一点F,使S△ADF=S△ABC,那么点F的所有可能位置是 .
一十四.作图-旋转变换(共1小题)
60.(2021春 浦东新区期末)如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(1,1),C(﹣3,1),△A1B1C1与△ABC关于原点O对称.
(1)写出点A1、B1、C1的坐标,并在右图中画出△A1B1C1;
(2)求△A1B1C1的面积.
参考答案与试题解析
五.一次函数图象上点的坐标特征(共1小题)
32.(2021春 金山区期末)如图,已知在平面直角坐标系xOy中,点A(﹣4,0),点B(2n﹣10,m+2),当点A向右平移m(m>0)个单位,再向上平移n(n>0)个单位时,可与点B重合.
(1)求点B的坐标;
(2)将点B向右平移3个单位后得到的点记为点C,点C恰好在直线x=b上,点D在直线x=b上,当△BCD是等腰三角形时,求点D的坐标.
【解答】解:∵点A(﹣4,0),点B(2n﹣10,m+2),且当点A向右平移m(m>0)个单位,再向上平移n(n>0)个单位时,可与点B重合,
∴﹣4+m=2n﹣10,且n=m+2,解得m=2,n=4,
∴点B的坐标为(﹣2,4);
(2)由(1)知点B(﹣2,4),
∵点B向右平移3个单位后得到的点记为点C,
∴点C(1,4).
∵点C恰好在直线x=b上,
∴x=1,
∵点D在直线x=1上,
∴BC⊥CD,设点D的坐标为(1,x),
∵△BCD是等腰三角形,
∴BC=CD,
∴1﹣(﹣2)=|x﹣4|,
即|x﹣4|=3,
∴x=7或1,
∴点D的坐标为(1,1)或(1,7).
六.平行线的性质(共3小题)
33.(2021春 浦东新区期末)如图,∠ABE=80°,BF是∠ABE的平分线,且BF∥CD,求∠C的度数.
【解答】解:∵BF是∠ABE的平分线,
∴∠ABF=∠ABE,
∵∠ABE=80°,
∴∠ABF=40°,
∵BF∥CD,
∴∠C=∠ABF,
∴∠C=40°.
34.(2021春 静安区校级期末)已知AB∥CD,且CD平分∠FCB,∠CEB=90°,∠CBE=40°,求∠EBA的度数.
【解答】解:∵∠CEB=90°,∠CBE=40°,
∴∠BCE=180°﹣90°﹣40°=50°,
∴∠FCB=180°﹣∠BCE=130°,
又∵CD平分∠FCB,
∴,
又∵AB∥CD,
∴∠CBA=∠BCD=65°,
∴∠EBA=∠CBA﹣∠CBE=65°﹣40°=25°.
35.(2021春 松江区期末)如图,已知在△ABC中,点D在边AC上,DA=DB,过点D作DE∥AB交边BC于点E,请说明∠BDE=∠CDE的理由.
【解答】证明:∵DA=DB,
∴∠DAB=∠DBA,
∵DE∥AB,
∴∠BDE=∠DBA,∠CDE=∠DAB,
∴∠BDE=∠CDE.
七.平行线的判定与性质(共7小题)
36.(2021春 嘉定区期末)如图,已知AD⊥BC,FG⊥BC,垂足分别为点D、G,∠1=∠2,试说明DE∥AC的理由.
解:因为AD⊥BC,FG⊥BC(已知),
所以∠ADC=90°,∠FGC=90°( 垂直的定义 ).
所以∠ADC=∠FGC(等量代换).
所以AD∥FG( 同位角相等,两直线平行 ).
所以∠1=∠CAD( 两直线平行,同位角相等 ),
因为∠1=∠2(已知).
所以∠2=∠CAD( 等量代换 ).
所以DE∥AC( 内错角相等,两直线平行 ).
【解答】解:∵AD⊥BC,FG⊥BC(已知),
∴∠ADC=90°,∠FGC=90°(垂直的定义),
∵∠ADC=∠FGC(等量代换),
∴AD∥FG(同位角相等,两直线平行),
∴∠1=∠CAD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠2=∠CAD(等量代换),
∴DE∥AC(内错角相等,两直线平行).
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.
37.(2021春 金山区期末)已知:如图,AB∥CD,AD和BC交于点O,E为OC上一点,F为CD上一点,且∠CEF+∠BOD=180°.求证:∠EFC=∠A.
【解答】证明:∵AB∥CD,
∴∠A=∠D,
∵∠CEF+∠BOD=180°,∠BOD+∠DOC=180°,
∴∠CEF=∠DOC.
∴EF∥AD.
∴∠EFC=∠D,
∵∠A=∠D,
∴∠EFC=∠A.
38.(2021春 静安区校级期末)如图,已知AB∥CD,∠1=∠2,∠3=∠4,请说明AD∥BC的理由.
解:因为AB∥CD(已知),
所以∠4=∠BAE( 两直线平行,同位角相等 ),
因为∠3=∠4(已知),
所以∠3=∠BAE( 等量代换 ),
因为∠1=∠2(已知),
所以∠1+∠CAE=∠2+∠CAE,
即∠BAE= ∠DAC .
所以∠3= ∠DAC .(等量代换)
因此AD∥BC( 内错角相等,两直线平行 ).
【解答】证明:因为AB∥CD(已知),
所以∠4=∠BAE(两直线平行,同位角相等),
因为∠3=∠4(已知)
所以∠3=∠BAE(等量代换),
因为∠1=∠2(已知),
所以∠CAE+∠1=∠CAE+∠2,
即∠BAE=∠DAC,
所以∠3=∠DAC,
因此AD∥BC(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;等量代换;∠DAC;∠DAC;内错角相等,两直线平行.
39.(2021春 松江区期末)阅读并填空:如图,AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
请说明∠GDB=∠C的理由.
解:因为AD⊥BC,EF⊥BC(已知),
所以∠ADC=∠EFC=90°( 垂直的定义 ).
所以EF∥AD( 同位角相等,两直线平行 ).
所以∠1+∠2=180°( 两直线平行,同旁内角互补 ).
又因为∠2+∠3=180°(已知),
所以∠1=∠3(同角的补角相等).
所以 AC ∥ DG (内错角相等,两直线平行).
所以∠GDB=∠C( 两直线平行,同位角相等 ).
【解答】解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADC=∠EFC=90°(垂直的定义),
∴EF∥AD (同位角相等,两直线平行),
∴∠1+∠2=180°(两直线平行,同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AC∥DG(内错角相等,两直线平行),
∴∠GDC=∠BC(两直线平行,同位角相等).
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,同旁内角互补;AC;DG;内错角相等,两直线平行;两直线平行,同位角相等.
40.(2021春 杨浦区期末)如图,已知∠ADE=∠B,∠1+∠2=180°,CD⊥AB,请填写理由,说明GF⊥AB.
解:因为∠ADE=∠B(已知),所以DE∥BC( 同位角相等,两直线平行 ).
得∠1=∠3( 两直线平行,内错角相等 ).
又因为∠1+∠2=180°(已知),所以∠2+∠3=180°( 等量代换 ).
所以 CD ∥ FG ( 同旁内角互补,两直线平行 ).
所以∠FGB=∠CDB( 两直线平行,同位角相等 ).
因为CD⊥AB(已知),所以∠CDB=90°(垂直的意义).
得∠FGB=90°,
所以GF⊥AB(垂直的意义).
【解答】解:∵∠ADE=∠B(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠1=∠3(两直线平行,内错角相等),
∵∠1+∠2=180°(已知),
∴∠2+∠3=180°(等量代换),
∴CD∥FG(同旁内角互补,两直线平行),
∴∠FGB=∠CDB(两直线平行,同位角相等),
∵CD⊥AB(已知),
∴∠CDB=90°(垂直的定义),
∴∠FGB=90°,
∴GF⊥AB(垂直的定义).
故答案为:同位角相等,两直线平行;两直线平行,内错角相等;等量代换;CD;FG;同旁内角互补,两直线平行;两直线平行,同位角相等.
41.(2021春 闵行区期末)如图,已知∠AHF=130°,∠CGE=50°,那么AB∥CD吗?为什么?
解:AB∥CD.
理由如下:
因为∠AHF+∠AHE=180°( 邻补角的意义 ),
又因为∠AHF=130°(已知),
所以∠AHE=180°﹣∠AHF=180°﹣130°=50°(等式性质).
因为∠CGE=50°(已知),
得∠CGE=∠AHE( 等量代换 ).
所以AB∥CD( 同位角相等,两直线平行 ).
【解答】解:AB∥CD.
理由如下:
因为∠AHF+∠AHE=180°(邻补角的意义),
又因为∠AHF=130°(已知),
所以∠AHE=180°﹣∠AHF=180°﹣130°=50°(等式性质).
因为∠CGE=50°(已知),
得∠CGE=∠AHE(等量代换).
所以AB∥CD(同位角相等,两直线平行).
故答案为:邻补角的意义;等量代换,同位角相等,两直线平行.
42.(2021春 浦东新区校级期末)已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 DE ∥ BC ( 同位角相等,两直线平行 )
所以∠B+∠BDE=180° ( 两直线平行,同旁内角互补 )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° ( 等量代换 )
所以 EF ∥ AB ( 同旁内角互补,两直线平行, )
所以∠1=∠2 ( 两直线平行,内错角相等 ).
【解答】解:因为∠AED=∠C(已知)
所以 DE∥BC( 同位角相等,两直线平行)
所以∠B+∠BDE=180° ( 两直线平行,同旁内角互补)
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° (等量代换 )
所以 EF∥AB(同旁内角互补,两直线平行 )
所以∠1=∠2 ( 两直线平行,内错角相等).
故答案为:DE,BC,同位角相等,两直线平行,两直线平行,同旁内角互补,等量代换 EF,AB,同旁内角互补,两直线平行,两直线平行,内错角相等.
八.三角形内角和定理(共1小题)
43.(2021春 静安区校级期末)如图,△ABC中,已知∠B=60°,∠ACD:∠A=5:2,求∠A的度数.
【解答】解:设∠A=2x°.
∵∠ACD:∠A=5:2,则∠ACD=5x°.
在△ABC中,
∠ACB=180°﹣∠A﹣∠B=180°﹣2x°﹣60°=120°﹣2x°,
∠ACB+∠ACD=120°﹣2x°+5x°=180°,
解得x=20,
∴∠A=2x°=40°.
九.三角形的外角性质(共1小题)
44.(2021春 静安区校级期末)△ABC中,∠A、∠B、∠C的外角的度数之比是2:3:4,求∠A的度数.
【解答】解:设∠A的外角为2x,则∠B的外角为3x,∠C的外角为4x,
∵任意多边形的外角和为360°,
∴2x+3x+4x=360°,
解得:x=40°,
∴∠A的外角为80°,
∴∠A=100°.
一十.全等三角形的判定与性质(共10小题)
45.(2021春 黄浦区期末)如图,点A、B、C、D在一条直线上如果AC=BD,BE=CF,且BE∥CF,那么AE∥DF.为什么?
解:∵BE∥CF(已知),
∴∠EBC=∠FCB( 两直线平行,内错角相等 ).
∵∠EBC+∠EBA=180°,∠FCB+∠FCD=180°(平角的意义),
∴∠EBA=∠FCD( 等角的补角相等 ).
∵AC=BD(已知),
∴AC﹣BC=BD﹣BC(等式性质),
即 AB=CD .(完成以下说理过程)
【解答】解:∵BE∥CF(已知),
∴∠EBC=∠FCB( 两直线平行,内错角相等).
∵∠EBC+∠EBA=180°,∠FCB+∠FCD=180°(平角的意义),
∴∠EBA=∠FCD( 等角的补角相等).
∵AC=BD(已知),
∴AC﹣BC=BD﹣BC(等式性质),
即AB=CD.
在△ABE和△DCF中
,
∴△ABE≌△DCF(SAS),
∴∠A=∠D,
∴AE∥DF.
故答案为:两直线平行,内错角相等;等角的补角相等;AB=CD.
46.(2021春 静安区校级期末)已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.若AB=5,求AD的长.
【解答】解:∵AC⊥BC于C,DE⊥AC于E,
∴∠C=∠AED=90°,∠CAB+∠B=90°,
∵AD⊥AB于A,
∴∠CAB+∠EAD=90°,
∴∠B=∠EAD(同角的余角相等)
∵BC=AE,∠C=∠AED=90°,∠B=∠EAD,
∴△ABC≌△DAE(AAS),
∴AD=AB=5.
47.(2021春 静安区校级期末)如图,在等边三角形ABC中,D、E分别是边AB、AC上的动点且AD=CE,连接DC、BE,记交点为F,试问DC、BE所成的∠BFC的大小有无变化?说明理由.
【解答】解:不变化,理由:
∵AD=CE,
∵在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS),
∴∠EBC=∠ACD,
∵∠BFC=180°﹣∠EBC﹣∠BCD,
∴∠BFC=180°﹣∠ACD﹣∠BCD,
=180°﹣∠ACB,
∵∠A=∠ABC=∠ACB,
∴∠ACB=60°,
∴∠BFC=180°﹣60°=120°,
∴∠BFC无变化.
48.(2021春 静安区校级期末)填空并续写解题过程:
如图,已知AB=AC,∠1=∠2=∠3,BE=EF,说明BC=FC的理由.
解:因为AB=AC,∠1=∠2,
所以 AD ⊥ BC (等腰三角形三线合一),
所以∠ADC=90°(垂直的意义).
因为∠ADC+∠2+∠ACD=180°,∠BEC+∠3+∠BCE=180°( 三角形内角和定理 ),
所以∠ADC+∠2+∠ACD=∠BEC+∠3+∠BCE.
又因为∠2=∠3(已知),
所以∠BEC=∠ ADC =90°(等式性质).
请续写解题过程,说明BC=FC的理由.
【解答】解:因为AB=AC,∠1=∠2,
所以AD⊥BC(三线合一),
所以∠ADC=90°(垂直的意义),
因为∠ADC+∠2+∠ACD=180°,∠BEC+∠3+∠BCE=180°(三角形内角和定理),
所以∠ADC+∠2+∠ACD=∠BEC+∠3+∠BCE,
又∠2=∠3(已知),
所以∠BEC=∠ADC=90°(等式性质),
因为∠BEC+∠FEC=180°(邻补角的意义),
所以∠FEC=90°(等式性质),
所以∠BEC=∠FEC(等量代换),
在△BEC与△FEC中,
,
所以△BEC≌△FEC(SAS),
∴BC=FC(全等三角形的对应边相等).
故答案为:AD,BC,三角形内角和定理;ADC.
49.(2021春 金山区期末)阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,说明BD=CE的理由.
解:因为AB=AC,
所以 ∠B=∠C ;(等边对等角)
因为 AD=AE ,(已知)
所以∠AED=∠ADE;(等边对等角)
因为∠AED=∠EAC+∠C,
∠ADE=∠BAD+∠B,( 三角形外角的性质 )
所以∠BAD=∠EAC;(等式性质)
在△ABD与△ACE中,
所以△ABD≌△ACE(A.S.A)
所以 BD=CE .(全等三角形的对应边相等)
【解答】解:因为AB=AC,
所以∠B=∠C;(等边对等角)
因为 AD=AE,(已知)
所以∠AED=∠ADE;(等边对等角)
因为∠AED=∠EAC+∠C,
∠ADE=∠BAD+∠B,( 三角形外角的性质)
所以∠BAD=∠EAC;(等式性质)
在△ABD与△ACE中,
,
所以△ABD≌△ACE(ASA)
所以 BD=CE.(全等三角形的对应边相等)
故答案为:∠B=∠C,AD=AE,三角形外角的性质,BD=CE.
50.(2021春 闵行区期末)如图,△ABC中,AD⊥BC,垂足为点D,CE⊥AB,垂足为点E,AD=DC,CE和AD交于点F,联结BF,试说明∠FBD=45°.
【解答】解:∵AD⊥BC,CE⊥AB,
∴∠ADC=∠ADB=90°=∠CEB,
∴∠ABD+∠BAD=90°=∠BCE+∠ABD,
∴∠BAD=∠BCE,
在△ABD和△CFD中,
,
∴△ABD≌△CFD(ASA),
∴BD=DF,
又∵∠ADB=90°,
∴∠FBD=45°.
51.(2021春 闵行区期末)如图,已知在等腰△ABC中AB=AC,点D,点E和点F分别是BC,AB和AC边上的点,且BE=DC,∠B=∠EDF,试说明DE=DF.
【解答】解:∵AB=AC,
∴∠B=∠C,
∵∠B=∠EDF,
∴∠C=∠EDF,
∵∠EDC=∠B+∠BED=∠EDF+∠FDC,
∴∠BED=∠CDF,
在△BDE和△CFD中,
,
∴△BDE≌△CFD(ASA),
∴DE=DF.
52.(2021春 浦东新区校级期末)如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
(1)试说明Rt△ABF≌Rt△DCE的理由;
(2)试说明OE=OF的理由.
【解答】解:(1)∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL);
(2)∵Rt△ABF≌Rt△DCE,
∴∠AFB=∠DEC,
∴OE=OF.
53.(2021春 浦东新区校级期末)如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
【解答】解:∵AE⊥DE,
∴∠AED=90°,
又∵∠B=90°,
∴∠B=∠AED,
∵∠AEC=∠B+∠BAE,
即∠AED+∠DEC=∠B+∠BAE,
∴∠BAE=∠DEC,
在△ABE与△ECD中,
,
∴△ABE≌△ECD(ASA),
∴AE=ED,
∵EF⊥AD,
∴点F是AD的中点.
54.(2021春 浦东新区校级期末)如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=44°,求∠BDE的度数.
【解答】(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA);
(2)解:∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=44°,
∴∠C=∠EDC=68°,
∴∠BDE=∠C=68°.
一十一.等腰三角形的性质(共1小题)
55.(2021春 闵行区期末)已知在等腰△ABC中AB=AC,∠B=2∠A,求∠B的度数.
【解答】解:∵等腰△ABC中AB=AC,
∴∠B=∠C,
∵∠B=2∠A,
∴∠B=∠C=2∠A,
设∠A=x°,
则∠B=∠C=2x°,
∵∠A+∠B+∠C=180°,
∴2x+2x+x=180,
解得:x=36,
∴∠B=2x=2×36°=72°.
一十二.等腰三角形的判定(共1小题)
56.(2021春 松江区期末)如图,已知在△ABC中,AB=AC=BD,∠ADE=∠B,请说明△ADE是等腰三角形的理由.
【解答】解:∵AB=BD,
∴∠BAD=∠BDA,
∵∠ADE=∠B,∠ADE+∠BAD+∠AED=180°,∠B+∠BDA+∠BAD=180°,
∴∠AED=∠BAD,
∴ED=AD,
∴△ADE为等腰三角形.
一十三.关于原点对称的点的坐标(共3小题)
57.(2021春 静安区校级期末)已知点A的坐标为(﹣3,2),设点A关于x轴对称的点为点B,点A关于原点的对称点为点C,过点C作y轴的平行线交x轴于点D,
(1)点B的坐标是 (﹣3,﹣2) ,点C的坐标是 (3,﹣2) .
(2)已知在线段BC上存在一点E,恰好能使△ABE≌△DEC,那么此时点E的坐标是 (﹣1,﹣2) .
【解答】解:(1)∵A的坐标为(﹣3,2),设点A关于x轴对称的点为点B,点A关于原点的对称点为点C,过点C作y轴的平行线,交x轴于点D.
∴点B的坐标是(﹣3,﹣2);点C的坐标是(3,﹣2).
故答案为:(﹣3,﹣2);(3,﹣2).
(2)如图所示:
∵若△ABE≌△ECD,
∴AB=CE,BE=CD,
∵AB=4,CD=2,
∴BE=2,CE=4,
∴点E坐标为(﹣1,﹣2).
58.(2021春 静安区校级期末)如图,在直角坐标平面内,已知点A的坐标是(0,4).
(1)图中B点的坐标是 (﹣2,3) .
(2)点B关于原点对称的点C的坐标是 (2,﹣3) ;点A关于x轴对称的点D的坐标是 (0,﹣4) .
(3)△ABC的面积是 8 .
(4)如果点E在x轴上,且S△ADE=S△ABC,那么点E的坐标是 (2,0)或(﹣2,0) .
【解答】解:(1)由题意得:
图中B点的坐标是(﹣2,3),
故答案为:(﹣2,3);
(2)∵B与C关于原点对称,B(﹣2,3),
∴C(2,﹣3),
∵A与D关于x轴对称,A(0,4),
∴D(0,﹣4),
故答案为:(2,﹣3),(0,﹣4);
(3)如图:
=28﹣1﹣7﹣12
=8;
(4)∵A(0,4),D(0,﹣4),
∴AD=4﹣(﹣4)=4+4=8,
∵,
∴,
∴|xE|=2,
∴E(2,0)或(﹣2,0).
59.(2021春 浦东新区校级期末)如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是 (﹣3,4) ;
(2)点B关于原点对称的点C的坐标是 (3,﹣4) ;点A关于y轴对称的点D的坐标是 (2,0) ;
(3)四边形ABDC的面积是 16 ;
(4)在y轴上找一点F,使S△ADF=S△ABC,那么点F的所有可能位置是 (0,4)或(0,﹣4) .
【解答】解:如图,
(1)过点B作x轴的垂线,垂足所对应的数为﹣3,因此点B的横坐标为﹣3,
过点B作y轴的垂线,垂足所对应的数为4,因此点B的纵坐标为4,
所以点B(﹣3,4);
故答案为:(﹣3,4);
(2)由于关于原点对称的两个点坐标纵横坐标均为互为相反数,
所以点B(﹣3,4)关于原点对称点C(3,﹣4),
由于关于y轴对称的两个点,其横坐标互为相反数,其纵坐标不变,
所以点A(﹣2,0)关于y轴对称点D(2,0),
故答案为:(3,﹣4),(2,0);
(3)S平行四边形ABCD=2S△ABD=2××4×4=16,
故答案为:16;
(4)因为S△ABC=S平行四边形ABCD=8=S△ADF,
所以AD OF=8,
∴OF=4,
又∵点F在y轴上,
∴点F(0,4)或(0,﹣4),
故答案为:(0,4)或(0,﹣4).
一十四.作图-旋转变换(共1小题)
60.(2021春 浦东新区期末)如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(1,1),C(﹣3,1),△A1B1C1与△ABC关于原点O对称.
(1)写出点A1、B1、C1的坐标,并在右图中画出△A1B1C1;
(2)求△A1B1C1的面积.
【解答】解:(1)如图,△A1B1C1为所作,点A1、B1、C1的坐标分别为(1,2),(﹣1,﹣1),(3,﹣1);
(2)△A1B1C1的面积=×4×3=6.
五.一次函数图象上点的坐标特征(共1小题)
32.(2021春 金山区期末)如图,已知在平面直角坐标系xOy中,点A(﹣4,0),点B(2n﹣10,m+2),当点A向右平移m(m>0)个单位,再向上平移n(n>0)个单位时,可与点B重合.
(1)求点B的坐标;
(2)将点B向右平移3个单位后得到的点记为点C,点C恰好在直线x=b上,点D在直线x=b上,当△BCD是等腰三角形时,求点D的坐标.
六.平行线的性质(共3小题)
33.(2021春 浦东新区期末)如图,∠ABE=80°,BF是∠ABE的平分线,且BF∥CD,求∠C的度数.
34.(2021春 静安区校级期末)已知AB∥CD,且CD平分∠FCB,∠CEB=90°,∠CBE=40°,求∠EBA的度数.
35.(2021春 松江区期末)如图,已知在△ABC中,点D在边AC上,DA=DB,过点D作DE∥AB交边BC于点E,请说明∠BDE=∠CDE的理由.
七.平行线的判定与性质(共7小题)
36.(2021春 嘉定区期末)如图,已知AD⊥BC,FG⊥BC,垂足分别为点D、G,∠1=∠2,试说明DE∥AC的理由.
解:因为AD⊥BC,FG⊥BC(已知),
所以∠ADC=90°,∠FGC=90°( ).
所以∠ADC=∠FGC(等量代换).
所以AD∥FG( ).
所以∠1=∠CAD( ),
因为∠1=∠2(已知).
所以∠2=∠CAD( ).
所以DE∥AC( ).
37.(2021春 金山区期末)已知:如图,AB∥CD,AD和BC交于点O,E为OC上一点,F为CD上一点,且∠CEF+∠BOD=180°.求证:∠EFC=∠A.
38.(2021春 静安区校级期末)如图,已知AB∥CD,∠1=∠2,∠3=∠4,请说明AD∥BC的理由.
解:因为AB∥CD(已知),
所以∠4=∠BAE( ),
因为∠3=∠4(已知),
所以∠3=∠BAE( ),
因为∠1=∠2(已知),
所以∠1+∠CAE=∠2+∠CAE,
即∠BAE= .
所以∠3= .(等量代换)
因此AD∥BC( ).
39.(2021春 松江区期末)阅读并填空:如图,AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
请说明∠GDB=∠C的理由.
解:因为AD⊥BC,EF⊥BC(已知),
所以∠ADC=∠EFC=90°( ).
所以EF∥AD( ).
所以∠1+∠2=180°( ).
又因为∠2+∠3=180°(已知),
所以∠1=∠3(同角的补角相等).
所以 ∥ (内错角相等,两直线平行).
所以∠GDB=∠C( ).
40.(2021春 杨浦区期末)如图,已知∠ADE=∠B,∠1+∠2=180°,CD⊥AB,请填写理由,说明GF⊥AB.
解:因为∠ADE=∠B(已知),所以DE∥BC( ).
得∠1=∠3( ).
又因为∠1+∠2=180°(已知),所以∠2+∠3=180°( ).
所以 ∥ ( ).
所以∠FGB=∠CDB( ).
因为CD⊥AB(已知),所以∠CDB=90°(垂直的意义).
得∠FGB=90°,
所以GF⊥AB(垂直的意义).
41.(2021春 闵行区期末)如图,已知∠AHF=130°,∠CGE=50°,那么AB∥CD吗?为什么?
解:AB∥CD.
理由如下:
因为∠AHF+∠AHE=180°( ),
又因为∠AHF=130°(已知),
所以∠AHE=180°﹣∠AHF=180°﹣130°=50°(等式性质).
因为∠CGE=50°(已知),
得∠CGE=∠AHE( ).
所以AB∥CD( ).
42.(2021春 浦东新区校级期末)已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ ( )
所以∠B+∠BDE=180° ( )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° ( )
所以 ∥ ( )
所以∠1=∠2 ( ).
八.三角形内角和定理(共1小题)
43.(2021春 静安区校级期末)如图,△ABC中,已知∠B=60°,∠ACD:∠A=5:2,求∠A的度数.
九.三角形的外角性质(共1小题)
44.(2021春 静安区校级期末)△ABC中,∠A、∠B、∠C的外角的度数之比是2:3:4,求∠A的度数.
一十.全等三角形的判定与性质(共10小题)
45.(2021春 黄浦区期末)如图,点A、B、C、D在一条直线上如果AC=BD,BE=CF,且BE∥CF,那么AE∥DF.为什么?
解:∵BE∥CF(已知),
∴∠EBC=∠FCB( ).
∵∠EBC+∠EBA=180°,∠FCB+∠FCD=180°(平角的意义),
∴∠EBA=∠FCD( ).
∵AC=BD(已知),
∴AC﹣BC=BD﹣BC(等式性质),
即 .(完成以下说理过程)
46.(2021春 静安区校级期末)已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.若AB=5,求AD的长.
47.(2021春 静安区校级期末)如图,在等边三角形ABC中,D、E分别是边AB、AC上的动点且AD=CE,连接DC、BE,记交点为F,试问DC、BE所成的∠BFC的大小有无变化?说明理由.
48.(2021春 静安区校级期末)填空并续写解题过程:
如图,已知AB=AC,∠1=∠2=∠3,BE=EF,说明BC=FC的理由.
解:因为AB=AC,∠1=∠2,
所以 ⊥ (等腰三角形三线合一),
所以∠ADC=90°(垂直的意义).
因为∠ADC+∠2+∠ACD=180°,∠BEC+∠3+∠BCE=180°( ),
所以∠ADC+∠2+∠ACD=∠BEC+∠3+∠BCE.
又因为∠2=∠3(已知),
所以∠BEC=∠ =90°(等式性质).
请续写解题过程,说明BC=FC的理由.
49.(2021春 金山区期末)阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,说明BD=CE的理由.
解:因为AB=AC,
所以 ;(等边对等角)
因为 ,(已知)
所以∠AED=∠ADE;(等边对等角)
因为∠AED=∠EAC+∠C,
∠ADE=∠BAD+∠B,( )
所以∠BAD=∠EAC;(等式性质)
在△ABD与△ACE中,
所以△ABD≌△ACE(A.S.A)
所以 .(全等三角形的对应边相等)
50.(2021春 闵行区期末)如图,△ABC中,AD⊥BC,垂足为点D,CE⊥AB,垂足为点E,AD=DC,CE和AD交于点F,联结BF,试说明∠FBD=45°.
51.(2021春 闵行区期末)如图,已知在等腰△ABC中AB=AC,点D,点E和点F分别是BC,AB和AC边上的点,且BE=DC,∠B=∠EDF,试说明DE=DF.
52.(2021春 浦东新区校级期末)如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
(1)试说明Rt△ABF≌Rt△DCE的理由;
(2)试说明OE=OF的理由.
53.(2021春 浦东新区校级期末)如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
54.(2021春 浦东新区校级期末)如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=44°,求∠BDE的度数.
一十一.等腰三角形的性质(共1小题)
55.(2021春 闵行区期末)已知在等腰△ABC中AB=AC,∠B=2∠A,求∠B的度数.
一十二.等腰三角形的判定(共1小题)
56.(2021春 松江区期末)如图,已知在△ABC中,AB=AC=BD,∠ADE=∠B,请说明△ADE是等腰三角形的理由.
一十三.关于原点对称的点的坐标(共3小题)
57.(2021春 静安区校级期末)已知点A的坐标为(﹣3,2),设点A关于x轴对称的点为点B,点A关于原点的对称点为点C,过点C作y轴的平行线交x轴于点D,
(1)点B的坐标是 ,点C的坐标是 .
(2)已知在线段BC上存在一点E,恰好能使△ABE≌△DEC,那么此时点E的坐标是 .
58.(2021春 静安区校级期末)如图,在直角坐标平面内,已知点A的坐标是(0,4).
(1)图中B点的坐标是 .
(2)点B关于原点对称的点C的坐标是 ;点A关于x轴对称的点D的坐标是 .
(3)△ABC的面积是 .
(4)如果点E在x轴上,且S△ADE=S△ABC,那么点E的坐标是 .
59.(2021春 浦东新区校级期末)如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是 ;
(2)点B关于原点对称的点C的坐标是 ;点A关于y轴对称的点D的坐标是 ;
(3)四边形ABDC的面积是 ;
(4)在y轴上找一点F,使S△ADF=S△ABC,那么点F的所有可能位置是 .
一十四.作图-旋转变换(共1小题)
60.(2021春 浦东新区期末)如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(1,1),C(﹣3,1),△A1B1C1与△ABC关于原点O对称.
(1)写出点A1、B1、C1的坐标,并在右图中画出△A1B1C1;
(2)求△A1B1C1的面积.
参考答案与试题解析
五.一次函数图象上点的坐标特征(共1小题)
32.(2021春 金山区期末)如图,已知在平面直角坐标系xOy中,点A(﹣4,0),点B(2n﹣10,m+2),当点A向右平移m(m>0)个单位,再向上平移n(n>0)个单位时,可与点B重合.
(1)求点B的坐标;
(2)将点B向右平移3个单位后得到的点记为点C,点C恰好在直线x=b上,点D在直线x=b上,当△BCD是等腰三角形时,求点D的坐标.
【解答】解:∵点A(﹣4,0),点B(2n﹣10,m+2),且当点A向右平移m(m>0)个单位,再向上平移n(n>0)个单位时,可与点B重合,
∴﹣4+m=2n﹣10,且n=m+2,解得m=2,n=4,
∴点B的坐标为(﹣2,4);
(2)由(1)知点B(﹣2,4),
∵点B向右平移3个单位后得到的点记为点C,
∴点C(1,4).
∵点C恰好在直线x=b上,
∴x=1,
∵点D在直线x=1上,
∴BC⊥CD,设点D的坐标为(1,x),
∵△BCD是等腰三角形,
∴BC=CD,
∴1﹣(﹣2)=|x﹣4|,
即|x﹣4|=3,
∴x=7或1,
∴点D的坐标为(1,1)或(1,7).
六.平行线的性质(共3小题)
33.(2021春 浦东新区期末)如图,∠ABE=80°,BF是∠ABE的平分线,且BF∥CD,求∠C的度数.
【解答】解:∵BF是∠ABE的平分线,
∴∠ABF=∠ABE,
∵∠ABE=80°,
∴∠ABF=40°,
∵BF∥CD,
∴∠C=∠ABF,
∴∠C=40°.
34.(2021春 静安区校级期末)已知AB∥CD,且CD平分∠FCB,∠CEB=90°,∠CBE=40°,求∠EBA的度数.
【解答】解:∵∠CEB=90°,∠CBE=40°,
∴∠BCE=180°﹣90°﹣40°=50°,
∴∠FCB=180°﹣∠BCE=130°,
又∵CD平分∠FCB,
∴,
又∵AB∥CD,
∴∠CBA=∠BCD=65°,
∴∠EBA=∠CBA﹣∠CBE=65°﹣40°=25°.
35.(2021春 松江区期末)如图,已知在△ABC中,点D在边AC上,DA=DB,过点D作DE∥AB交边BC于点E,请说明∠BDE=∠CDE的理由.
【解答】证明:∵DA=DB,
∴∠DAB=∠DBA,
∵DE∥AB,
∴∠BDE=∠DBA,∠CDE=∠DAB,
∴∠BDE=∠CDE.
七.平行线的判定与性质(共7小题)
36.(2021春 嘉定区期末)如图,已知AD⊥BC,FG⊥BC,垂足分别为点D、G,∠1=∠2,试说明DE∥AC的理由.
解:因为AD⊥BC,FG⊥BC(已知),
所以∠ADC=90°,∠FGC=90°( 垂直的定义 ).
所以∠ADC=∠FGC(等量代换).
所以AD∥FG( 同位角相等,两直线平行 ).
所以∠1=∠CAD( 两直线平行,同位角相等 ),
因为∠1=∠2(已知).
所以∠2=∠CAD( 等量代换 ).
所以DE∥AC( 内错角相等,两直线平行 ).
【解答】解:∵AD⊥BC,FG⊥BC(已知),
∴∠ADC=90°,∠FGC=90°(垂直的定义),
∵∠ADC=∠FGC(等量代换),
∴AD∥FG(同位角相等,两直线平行),
∴∠1=∠CAD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠2=∠CAD(等量代换),
∴DE∥AC(内错角相等,两直线平行).
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.
37.(2021春 金山区期末)已知:如图,AB∥CD,AD和BC交于点O,E为OC上一点,F为CD上一点,且∠CEF+∠BOD=180°.求证:∠EFC=∠A.
【解答】证明:∵AB∥CD,
∴∠A=∠D,
∵∠CEF+∠BOD=180°,∠BOD+∠DOC=180°,
∴∠CEF=∠DOC.
∴EF∥AD.
∴∠EFC=∠D,
∵∠A=∠D,
∴∠EFC=∠A.
38.(2021春 静安区校级期末)如图,已知AB∥CD,∠1=∠2,∠3=∠4,请说明AD∥BC的理由.
解:因为AB∥CD(已知),
所以∠4=∠BAE( 两直线平行,同位角相等 ),
因为∠3=∠4(已知),
所以∠3=∠BAE( 等量代换 ),
因为∠1=∠2(已知),
所以∠1+∠CAE=∠2+∠CAE,
即∠BAE= ∠DAC .
所以∠3= ∠DAC .(等量代换)
因此AD∥BC( 内错角相等,两直线平行 ).
【解答】证明:因为AB∥CD(已知),
所以∠4=∠BAE(两直线平行,同位角相等),
因为∠3=∠4(已知)
所以∠3=∠BAE(等量代换),
因为∠1=∠2(已知),
所以∠CAE+∠1=∠CAE+∠2,
即∠BAE=∠DAC,
所以∠3=∠DAC,
因此AD∥BC(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;等量代换;∠DAC;∠DAC;内错角相等,两直线平行.
39.(2021春 松江区期末)阅读并填空:如图,AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
请说明∠GDB=∠C的理由.
解:因为AD⊥BC,EF⊥BC(已知),
所以∠ADC=∠EFC=90°( 垂直的定义 ).
所以EF∥AD( 同位角相等,两直线平行 ).
所以∠1+∠2=180°( 两直线平行,同旁内角互补 ).
又因为∠2+∠3=180°(已知),
所以∠1=∠3(同角的补角相等).
所以 AC ∥ DG (内错角相等,两直线平行).
所以∠GDB=∠C( 两直线平行,同位角相等 ).
【解答】解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADC=∠EFC=90°(垂直的定义),
∴EF∥AD (同位角相等,两直线平行),
∴∠1+∠2=180°(两直线平行,同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AC∥DG(内错角相等,两直线平行),
∴∠GDC=∠BC(两直线平行,同位角相等).
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,同旁内角互补;AC;DG;内错角相等,两直线平行;两直线平行,同位角相等.
40.(2021春 杨浦区期末)如图,已知∠ADE=∠B,∠1+∠2=180°,CD⊥AB,请填写理由,说明GF⊥AB.
解:因为∠ADE=∠B(已知),所以DE∥BC( 同位角相等,两直线平行 ).
得∠1=∠3( 两直线平行,内错角相等 ).
又因为∠1+∠2=180°(已知),所以∠2+∠3=180°( 等量代换 ).
所以 CD ∥ FG ( 同旁内角互补,两直线平行 ).
所以∠FGB=∠CDB( 两直线平行,同位角相等 ).
因为CD⊥AB(已知),所以∠CDB=90°(垂直的意义).
得∠FGB=90°,
所以GF⊥AB(垂直的意义).
【解答】解:∵∠ADE=∠B(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠1=∠3(两直线平行,内错角相等),
∵∠1+∠2=180°(已知),
∴∠2+∠3=180°(等量代换),
∴CD∥FG(同旁内角互补,两直线平行),
∴∠FGB=∠CDB(两直线平行,同位角相等),
∵CD⊥AB(已知),
∴∠CDB=90°(垂直的定义),
∴∠FGB=90°,
∴GF⊥AB(垂直的定义).
故答案为:同位角相等,两直线平行;两直线平行,内错角相等;等量代换;CD;FG;同旁内角互补,两直线平行;两直线平行,同位角相等.
41.(2021春 闵行区期末)如图,已知∠AHF=130°,∠CGE=50°,那么AB∥CD吗?为什么?
解:AB∥CD.
理由如下:
因为∠AHF+∠AHE=180°( 邻补角的意义 ),
又因为∠AHF=130°(已知),
所以∠AHE=180°﹣∠AHF=180°﹣130°=50°(等式性质).
因为∠CGE=50°(已知),
得∠CGE=∠AHE( 等量代换 ).
所以AB∥CD( 同位角相等,两直线平行 ).
【解答】解:AB∥CD.
理由如下:
因为∠AHF+∠AHE=180°(邻补角的意义),
又因为∠AHF=130°(已知),
所以∠AHE=180°﹣∠AHF=180°﹣130°=50°(等式性质).
因为∠CGE=50°(已知),
得∠CGE=∠AHE(等量代换).
所以AB∥CD(同位角相等,两直线平行).
故答案为:邻补角的意义;等量代换,同位角相等,两直线平行.
42.(2021春 浦东新区校级期末)已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 DE ∥ BC ( 同位角相等,两直线平行 )
所以∠B+∠BDE=180° ( 两直线平行,同旁内角互补 )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° ( 等量代换 )
所以 EF ∥ AB ( 同旁内角互补,两直线平行, )
所以∠1=∠2 ( 两直线平行,内错角相等 ).
【解答】解:因为∠AED=∠C(已知)
所以 DE∥BC( 同位角相等,两直线平行)
所以∠B+∠BDE=180° ( 两直线平行,同旁内角互补)
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° (等量代换 )
所以 EF∥AB(同旁内角互补,两直线平行 )
所以∠1=∠2 ( 两直线平行,内错角相等).
故答案为:DE,BC,同位角相等,两直线平行,两直线平行,同旁内角互补,等量代换 EF,AB,同旁内角互补,两直线平行,两直线平行,内错角相等.
八.三角形内角和定理(共1小题)
43.(2021春 静安区校级期末)如图,△ABC中,已知∠B=60°,∠ACD:∠A=5:2,求∠A的度数.
【解答】解:设∠A=2x°.
∵∠ACD:∠A=5:2,则∠ACD=5x°.
在△ABC中,
∠ACB=180°﹣∠A﹣∠B=180°﹣2x°﹣60°=120°﹣2x°,
∠ACB+∠ACD=120°﹣2x°+5x°=180°,
解得x=20,
∴∠A=2x°=40°.
九.三角形的外角性质(共1小题)
44.(2021春 静安区校级期末)△ABC中,∠A、∠B、∠C的外角的度数之比是2:3:4,求∠A的度数.
【解答】解:设∠A的外角为2x,则∠B的外角为3x,∠C的外角为4x,
∵任意多边形的外角和为360°,
∴2x+3x+4x=360°,
解得:x=40°,
∴∠A的外角为80°,
∴∠A=100°.
一十.全等三角形的判定与性质(共10小题)
45.(2021春 黄浦区期末)如图,点A、B、C、D在一条直线上如果AC=BD,BE=CF,且BE∥CF,那么AE∥DF.为什么?
解:∵BE∥CF(已知),
∴∠EBC=∠FCB( 两直线平行,内错角相等 ).
∵∠EBC+∠EBA=180°,∠FCB+∠FCD=180°(平角的意义),
∴∠EBA=∠FCD( 等角的补角相等 ).
∵AC=BD(已知),
∴AC﹣BC=BD﹣BC(等式性质),
即 AB=CD .(完成以下说理过程)
【解答】解:∵BE∥CF(已知),
∴∠EBC=∠FCB( 两直线平行,内错角相等).
∵∠EBC+∠EBA=180°,∠FCB+∠FCD=180°(平角的意义),
∴∠EBA=∠FCD( 等角的补角相等).
∵AC=BD(已知),
∴AC﹣BC=BD﹣BC(等式性质),
即AB=CD.
在△ABE和△DCF中
,
∴△ABE≌△DCF(SAS),
∴∠A=∠D,
∴AE∥DF.
故答案为:两直线平行,内错角相等;等角的补角相等;AB=CD.
46.(2021春 静安区校级期末)已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.若AB=5,求AD的长.
【解答】解:∵AC⊥BC于C,DE⊥AC于E,
∴∠C=∠AED=90°,∠CAB+∠B=90°,
∵AD⊥AB于A,
∴∠CAB+∠EAD=90°,
∴∠B=∠EAD(同角的余角相等)
∵BC=AE,∠C=∠AED=90°,∠B=∠EAD,
∴△ABC≌△DAE(AAS),
∴AD=AB=5.
47.(2021春 静安区校级期末)如图,在等边三角形ABC中,D、E分别是边AB、AC上的动点且AD=CE,连接DC、BE,记交点为F,试问DC、BE所成的∠BFC的大小有无变化?说明理由.
【解答】解:不变化,理由:
∵AD=CE,
∵在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS),
∴∠EBC=∠ACD,
∵∠BFC=180°﹣∠EBC﹣∠BCD,
∴∠BFC=180°﹣∠ACD﹣∠BCD,
=180°﹣∠ACB,
∵∠A=∠ABC=∠ACB,
∴∠ACB=60°,
∴∠BFC=180°﹣60°=120°,
∴∠BFC无变化.
48.(2021春 静安区校级期末)填空并续写解题过程:
如图,已知AB=AC,∠1=∠2=∠3,BE=EF,说明BC=FC的理由.
解:因为AB=AC,∠1=∠2,
所以 AD ⊥ BC (等腰三角形三线合一),
所以∠ADC=90°(垂直的意义).
因为∠ADC+∠2+∠ACD=180°,∠BEC+∠3+∠BCE=180°( 三角形内角和定理 ),
所以∠ADC+∠2+∠ACD=∠BEC+∠3+∠BCE.
又因为∠2=∠3(已知),
所以∠BEC=∠ ADC =90°(等式性质).
请续写解题过程,说明BC=FC的理由.
【解答】解:因为AB=AC,∠1=∠2,
所以AD⊥BC(三线合一),
所以∠ADC=90°(垂直的意义),
因为∠ADC+∠2+∠ACD=180°,∠BEC+∠3+∠BCE=180°(三角形内角和定理),
所以∠ADC+∠2+∠ACD=∠BEC+∠3+∠BCE,
又∠2=∠3(已知),
所以∠BEC=∠ADC=90°(等式性质),
因为∠BEC+∠FEC=180°(邻补角的意义),
所以∠FEC=90°(等式性质),
所以∠BEC=∠FEC(等量代换),
在△BEC与△FEC中,
,
所以△BEC≌△FEC(SAS),
∴BC=FC(全等三角形的对应边相等).
故答案为:AD,BC,三角形内角和定理;ADC.
49.(2021春 金山区期末)阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,说明BD=CE的理由.
解:因为AB=AC,
所以 ∠B=∠C ;(等边对等角)
因为 AD=AE ,(已知)
所以∠AED=∠ADE;(等边对等角)
因为∠AED=∠EAC+∠C,
∠ADE=∠BAD+∠B,( 三角形外角的性质 )
所以∠BAD=∠EAC;(等式性质)
在△ABD与△ACE中,
所以△ABD≌△ACE(A.S.A)
所以 BD=CE .(全等三角形的对应边相等)
【解答】解:因为AB=AC,
所以∠B=∠C;(等边对等角)
因为 AD=AE,(已知)
所以∠AED=∠ADE;(等边对等角)
因为∠AED=∠EAC+∠C,
∠ADE=∠BAD+∠B,( 三角形外角的性质)
所以∠BAD=∠EAC;(等式性质)
在△ABD与△ACE中,
,
所以△ABD≌△ACE(ASA)
所以 BD=CE.(全等三角形的对应边相等)
故答案为:∠B=∠C,AD=AE,三角形外角的性质,BD=CE.
50.(2021春 闵行区期末)如图,△ABC中,AD⊥BC,垂足为点D,CE⊥AB,垂足为点E,AD=DC,CE和AD交于点F,联结BF,试说明∠FBD=45°.
【解答】解:∵AD⊥BC,CE⊥AB,
∴∠ADC=∠ADB=90°=∠CEB,
∴∠ABD+∠BAD=90°=∠BCE+∠ABD,
∴∠BAD=∠BCE,
在△ABD和△CFD中,
,
∴△ABD≌△CFD(ASA),
∴BD=DF,
又∵∠ADB=90°,
∴∠FBD=45°.
51.(2021春 闵行区期末)如图,已知在等腰△ABC中AB=AC,点D,点E和点F分别是BC,AB和AC边上的点,且BE=DC,∠B=∠EDF,试说明DE=DF.
【解答】解:∵AB=AC,
∴∠B=∠C,
∵∠B=∠EDF,
∴∠C=∠EDF,
∵∠EDC=∠B+∠BED=∠EDF+∠FDC,
∴∠BED=∠CDF,
在△BDE和△CFD中,
,
∴△BDE≌△CFD(ASA),
∴DE=DF.
52.(2021春 浦东新区校级期末)如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
(1)试说明Rt△ABF≌Rt△DCE的理由;
(2)试说明OE=OF的理由.
【解答】解:(1)∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL);
(2)∵Rt△ABF≌Rt△DCE,
∴∠AFB=∠DEC,
∴OE=OF.
53.(2021春 浦东新区校级期末)如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
【解答】解:∵AE⊥DE,
∴∠AED=90°,
又∵∠B=90°,
∴∠B=∠AED,
∵∠AEC=∠B+∠BAE,
即∠AED+∠DEC=∠B+∠BAE,
∴∠BAE=∠DEC,
在△ABE与△ECD中,
,
∴△ABE≌△ECD(ASA),
∴AE=ED,
∵EF⊥AD,
∴点F是AD的中点.
54.(2021春 浦东新区校级期末)如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=44°,求∠BDE的度数.
【解答】(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA);
(2)解:∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=44°,
∴∠C=∠EDC=68°,
∴∠BDE=∠C=68°.
一十一.等腰三角形的性质(共1小题)
55.(2021春 闵行区期末)已知在等腰△ABC中AB=AC,∠B=2∠A,求∠B的度数.
【解答】解:∵等腰△ABC中AB=AC,
∴∠B=∠C,
∵∠B=2∠A,
∴∠B=∠C=2∠A,
设∠A=x°,
则∠B=∠C=2x°,
∵∠A+∠B+∠C=180°,
∴2x+2x+x=180,
解得:x=36,
∴∠B=2x=2×36°=72°.
一十二.等腰三角形的判定(共1小题)
56.(2021春 松江区期末)如图,已知在△ABC中,AB=AC=BD,∠ADE=∠B,请说明△ADE是等腰三角形的理由.
【解答】解:∵AB=BD,
∴∠BAD=∠BDA,
∵∠ADE=∠B,∠ADE+∠BAD+∠AED=180°,∠B+∠BDA+∠BAD=180°,
∴∠AED=∠BAD,
∴ED=AD,
∴△ADE为等腰三角形.
一十三.关于原点对称的点的坐标(共3小题)
57.(2021春 静安区校级期末)已知点A的坐标为(﹣3,2),设点A关于x轴对称的点为点B,点A关于原点的对称点为点C,过点C作y轴的平行线交x轴于点D,
(1)点B的坐标是 (﹣3,﹣2) ,点C的坐标是 (3,﹣2) .
(2)已知在线段BC上存在一点E,恰好能使△ABE≌△DEC,那么此时点E的坐标是 (﹣1,﹣2) .
【解答】解:(1)∵A的坐标为(﹣3,2),设点A关于x轴对称的点为点B,点A关于原点的对称点为点C,过点C作y轴的平行线,交x轴于点D.
∴点B的坐标是(﹣3,﹣2);点C的坐标是(3,﹣2).
故答案为:(﹣3,﹣2);(3,﹣2).
(2)如图所示:
∵若△ABE≌△ECD,
∴AB=CE,BE=CD,
∵AB=4,CD=2,
∴BE=2,CE=4,
∴点E坐标为(﹣1,﹣2).
58.(2021春 静安区校级期末)如图,在直角坐标平面内,已知点A的坐标是(0,4).
(1)图中B点的坐标是 (﹣2,3) .
(2)点B关于原点对称的点C的坐标是 (2,﹣3) ;点A关于x轴对称的点D的坐标是 (0,﹣4) .
(3)△ABC的面积是 8 .
(4)如果点E在x轴上,且S△ADE=S△ABC,那么点E的坐标是 (2,0)或(﹣2,0) .
【解答】解:(1)由题意得:
图中B点的坐标是(﹣2,3),
故答案为:(﹣2,3);
(2)∵B与C关于原点对称,B(﹣2,3),
∴C(2,﹣3),
∵A与D关于x轴对称,A(0,4),
∴D(0,﹣4),
故答案为:(2,﹣3),(0,﹣4);
(3)如图:
=28﹣1﹣7﹣12
=8;
(4)∵A(0,4),D(0,﹣4),
∴AD=4﹣(﹣4)=4+4=8,
∵,
∴,
∴|xE|=2,
∴E(2,0)或(﹣2,0).
59.(2021春 浦东新区校级期末)如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是 (﹣3,4) ;
(2)点B关于原点对称的点C的坐标是 (3,﹣4) ;点A关于y轴对称的点D的坐标是 (2,0) ;
(3)四边形ABDC的面积是 16 ;
(4)在y轴上找一点F,使S△ADF=S△ABC,那么点F的所有可能位置是 (0,4)或(0,﹣4) .
【解答】解:如图,
(1)过点B作x轴的垂线,垂足所对应的数为﹣3,因此点B的横坐标为﹣3,
过点B作y轴的垂线,垂足所对应的数为4,因此点B的纵坐标为4,
所以点B(﹣3,4);
故答案为:(﹣3,4);
(2)由于关于原点对称的两个点坐标纵横坐标均为互为相反数,
所以点B(﹣3,4)关于原点对称点C(3,﹣4),
由于关于y轴对称的两个点,其横坐标互为相反数,其纵坐标不变,
所以点A(﹣2,0)关于y轴对称点D(2,0),
故答案为:(3,﹣4),(2,0);
(3)S平行四边形ABCD=2S△ABD=2××4×4=16,
故答案为:16;
(4)因为S△ABC=S平行四边形ABCD=8=S△ADF,
所以AD OF=8,
∴OF=4,
又∵点F在y轴上,
∴点F(0,4)或(0,﹣4),
故答案为:(0,4)或(0,﹣4).
一十四.作图-旋转变换(共1小题)
60.(2021春 浦东新区期末)如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(1,1),C(﹣3,1),△A1B1C1与△ABC关于原点O对称.
(1)写出点A1、B1、C1的坐标,并在右图中画出△A1B1C1;
(2)求△A1B1C1的面积.
【解答】解:(1)如图,△A1B1C1为所作,点A1、B1、C1的坐标分别为(1,2),(﹣1,﹣1),(3,﹣1);
(2)△A1B1C1的面积=×4×3=6.
同课章节目录
