08填空题(中档题)2021年春上海市各区七年级(下)期末数学知识点分类汇编
文档属性
| 名称 | 08填空题(中档题)2021年春上海市各区七年级(下)期末数学知识点分类汇编 |

|
|
| 格式 | doc | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 20:30:10 | ||
图片预览




文档简介
08填空题(中档题)
一.科学记数法与有效数字(共2小题)
1.(2021春 杨浦区期末)据第七次全国人口普查发布的数据显示,2020年上海市总人口约为24870000人,将24870000这个数保留两个有效数字并用科学记数法表示是 .
2.(2022 天山区校级二模)月球沿着一定的轨道围绕地球运动,某一时刻它与地球相距405 500千米,用科学记数法表示这个数并保留三个有效数字 .
二.平方根(共1小题)
3.(2021春 杨浦区期末)如果x2=25,则x= .
三.立方根(共1小题)
4.(2021春 静安区期末)已知a3=216,那么a= .
四.实数的运算(共1小题)
5.(2021 沙坪坝区校级模拟)计算:﹣|﹣3|= .
五.分数指数幂(共3小题)
6.(2021春 静安区期末)计算:4= .
7.(2021春 黄浦区期末)把表示成幂的形式是 .
8.(2021春 嘉定区期末)把表示成幂的形式是 .
六.二次根式的乘除法(共1小题)
9.(2021春 杨浦区期末)计算:= .
七.分母有理化(共1小题)
10.(2021春 奉贤区期末)计算:= .
八.二次根式的混合运算(共1小题)
11.(2021春 黄浦区期末)计算:(3+)2×(3﹣)2= .
九.点的坐标(共2小题)
12.(2021春 奉贤区期末)已知点P位于第四象限内,且点P到x轴的距离是2,到y轴的距离是4,则点P的坐标为 .
13.(2021春 静安区期末)在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 .
一十.坐标与图形性质(共2小题)
14.(2021春 奉贤区期末)经过点M(3,1)且平行于x轴的直线可以表示为直线 .
15.(2021春 浦东新区期末)在平面直角坐标系中,线段AB=3,且AB∥x轴,如果点A的坐标为(﹣1,2),那么点B的坐标是 .
一十一.平行线的性质(共2小题)
16.(2021春 金坛区期末)若∠A与∠B的一组边平行,另一组边垂直,且∠A﹣2∠B=15°,则∠B的度数为 .
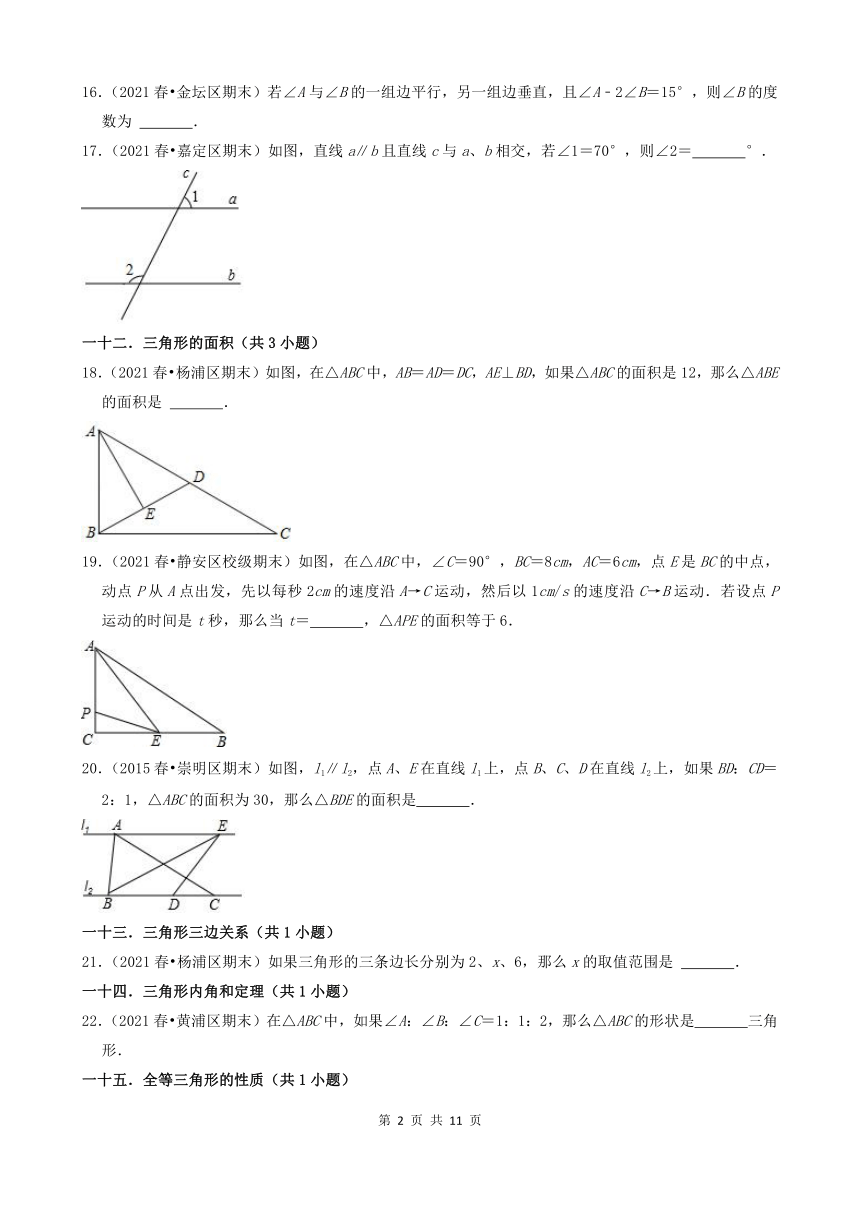
17.(2021春 嘉定区期末)如图,直线a∥b且直线c与a、b相交,若∠1=70°,则∠2= °.
一十二.三角形的面积(共3小题)
18.(2021春 杨浦区期末)如图,在△ABC中,AB=AD=DC,AE⊥BD,如果△ABC的面积是12,那么△ABE的面积是 .
19.(2021春 静安区校级期末)如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t= ,△APE的面积等于6.
20.(2015春 崇明区期末)如图,l1∥l2,点A、E在直线l1上,点B、C、D在直线l2上,如果BD:CD=2:1,△ABC的面积为30,那么△BDE的面积是 .
一十三.三角形三边关系(共1小题)
21.(2021春 杨浦区期末)如果三角形的三条边长分别为2、x、6,那么x的取值范围是 .
一十四.三角形内角和定理(共1小题)
22.(2021春 黄浦区期末)在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是 三角形.
一十五.全等三角形的性质(共1小题)
23.(2021春 浦东新区期末)如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 °.
一十六.全等三角形的判定(共1小题)
24.(2021春 奉贤区期末)如图,已知AC=DC,∠1=∠2,请添加一个条件,使△ABC≌△DEC,这个条件可以是 .
参考答案与试题解析
一.科学记数法与有效数字(共2小题)
1.(2021春 杨浦区期末)据第七次全国人口普查发布的数据显示,2020年上海市总人口约为24870000人,将24870000这个数保留两个有效数字并用科学记数法表示是 2.5×107 .
【解答】解:24870000=2.487×107≈2.5×107.
故答案是:2.5×107.
2.(2022 天山区校级二模)月球沿着一定的轨道围绕地球运动,某一时刻它与地球相距405 500千米,用科学记数法表示这个数并保留三个有效数字 4.06×105 .
【解答】解:405 500千米=4.055×105千米≈4.06×105千米.
故答案为4.06×105.
二.平方根(共1小题)
3.(2021春 杨浦区期末)如果x2=25,则x= ±5 .
【解答】解:∵x2=25,
∴x=±5,
故答案为:±5.
三.立方根(共1小题)
4.(2021春 静安区期末)已知a3=216,那么a= 6 .
【解答】解:因为a3=216,
所以a==6.
故答案为:6.
四.实数的运算(共1小题)
5.(2021 沙坪坝区校级模拟)计算:﹣|﹣3|= ﹣5 .
【解答】解:﹣|﹣3|
=﹣2﹣3
=﹣5.
故答案为:﹣5.
五.分数指数幂(共3小题)
6.(2021春 静安区期末)计算:4= .
【解答】解:因为4=22,所以
7.(2021春 黄浦区期末)把表示成幂的形式是 .
【解答】解:把表示成幂的形式是.
故答案为.
8.(2021春 嘉定区期末)把表示成幂的形式是 .
【解答】解:
故答案为:.
六.二次根式的乘除法(共1小题)
9.(2021春 杨浦区期末)计算:= .
【解答】解:
=
=.
故答案为:.
七.分母有理化(共1小题)
10.(2021春 奉贤区期末)计算:= 2 .
【解答】解:原式=×
=
=2,
故答案为:2.
八.二次根式的混合运算(共1小题)
11.(2021春 黄浦区期末)计算:(3+)2×(3﹣)2= 49 .
【解答】解:(3+)2×(3﹣)2
=[(3+)×(3﹣)]2
=[]2
=72
=49.
故答案为:49.
九.点的坐标(共2小题)
12.(2021春 奉贤区期末)已知点P位于第四象限内,且点P到x轴的距离是2,到y轴的距离是4,则点P的坐标为 (4,﹣2) .
【解答】解:因为点P在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点P到x轴和y轴的距离分别是2和4,
所以点P的坐标为(4,﹣2).
故答案为(4,﹣2).
13.(2021春 静安区期末)在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 ﹣1或0 .
【解答】解:∵格点P(2m﹣1,m+2)在第二象限,
∴,
解不等式①得,m<,
解不等式②得,m>﹣2,
∴不等式的解集为﹣2<m<,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为﹣1或0.
故答案为:﹣1或0.
一十.坐标与图形性质(共2小题)
14.(2021春 奉贤区期末)经过点M(3,1)且平行于x轴的直线可以表示为直线 y=1 .
【解答】解:∵所求直线经过点M(3,1)且平行于x轴,
∴该直线上所有点纵坐标都是1,
故可以表示为直线y=1.
故答案为:y=1.
15.(2021春 浦东新区期末)在平面直角坐标系中,线段AB=3,且AB∥x轴,如果点A的坐标为(﹣1,2),那么点B的坐标是 (﹣4,2),(2,2) .
【解答】解:∵AB∥x轴且A(﹣1,2),
∴点B的纵坐标为2,
又∵AB=3,
∴点B的横坐标为﹣1+3=2或﹣1﹣3=﹣4,
∴点B的坐标为(2,2)或(﹣4,2),
故答案为:(﹣4,2),(2,2).
一十一.平行线的性质(共2小题)
16.(2021春 金坛区期末)若∠A与∠B的一组边平行,另一组边垂直,且∠A﹣2∠B=15°,则∠B的度数为 75°或25° .
【解答】解:如图1:
∵AE∥BF,
∴∠A+∠1=180°,
∴∠1=180°﹣∠A,
∵∠A﹣2∠B=15°,
∴∠1=180°﹣(2∠B+15°)=165°﹣2∠B,
∵AC⊥BC,
∴∠1+∠B=90°,
∴165°﹣2∠B+∠B=90°,
∴∠B=75°;
如图2:
∵AE∥BF,
∴∠A=∠1,
∵∠A﹣2∠B=15°,
∴∠1=2∠B+15°,
∵AC⊥BC,
∴∠1+∠B=90°,
∴2∠B+15°+∠B=90°,
∴∠B=25°;
综上,∠B的度数为75°或25°.
故答案为:75°或25°.
17.(2021春 嘉定区期末)如图,直线a∥b且直线c与a、b相交,若∠1=70°,则∠2= 110 °.
【解答】解:如图,
∵a∥b,
∴∠1=∠3,
∵∠1=70°,
∴∠3=70°,
∴∠2=180°﹣∠3=110°,
故答案为110.
一十二.三角形的面积(共3小题)
18.(2021春 杨浦区期末)如图,在△ABC中,AB=AD=DC,AE⊥BD,如果△ABC的面积是12,那么△ABE的面积是 3 .
【解答】解:∵AB=AD=AC,
∴D是△ABC的中线,
∴S△ABD=S△ABC=12=6,
∵△ABD是等腰三角形,AE⊥BD,
∴点E是BD的中点,
∴S△ABE=S△ABD=6=3.
故答案为:3.
19.(2021春 静安区校级期末)如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t= 1.5s或5s或9s ,△APE的面积等于6.
【解答】解:如图1,当点P在AC上,
∵△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,
∴CE=4,AP=2t.
∵△APE的面积等于6,
∴S△APE=AP CE=×2t×4=6,
∴t=1.5;
如图2,当点P在线段CE上,
∵E是DC的中点,
∴BE=CE=4.
∴PE=4﹣(t﹣3)=7﹣t,
∴S=EP AC= (7﹣t)×6=6,
∴t=5,
如图3,当P在线段BE上,
同理:PE=t﹣3﹣4=t﹣7,
∴S=EP AC= (t﹣7)×6=6,
∴t=9,
综上所述,t的值为1.5或5或9;
故答案为:1.5或5或9.
20.(2015春 崇明区期末)如图,l1∥l2,点A、E在直线l1上,点B、C、D在直线l2上,如果BD:CD=2:1,△ABC的面积为30,那么△BDE的面积是 20 .
【解答】解:∵l1∥l2,
∴△BDE的面积:△ABC的面积=BD:BC=2:3,
∴△BDE的面积=30×=20.
故答案为:20.
一十三.三角形三边关系(共1小题)
21.(2021春 杨浦区期末)如果三角形的三条边长分别为2、x、6,那么x的取值范围是 4<x<8 .
【解答】解:根据题意得:6﹣2<x<6+2,
即4<x<8.
故答案为:4<x<8.
一十四.三角形内角和定理(共1小题)
22.(2021春 黄浦区期末)在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是 等腰直角 三角形.
【解答】解:设一份为k°,则三个内角的度数分别为k°,k°,2k°.
则k°+k°+2k°=180°,
解得k°=45°.
∴2k°=90°,
所以这个三角形是等腰直角三角形.
故应填:等腰直角.
一十五.全等三角形的性质(共1小题)
23.(2021春 浦东新区期末)如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 36 °.
【解答】解:∵△ABC≌△ADE,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠BAD=40°,
∴∠ABD=∠ADB=(180°﹣∠BAD)=70°,
∵△ABC≌△ADE,
∴∠ADE=∠ABD=70°,
∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=114°﹣40°=74°,
∴∠E=180°﹣∠ADE﹣∠DAE=180°﹣70°﹣74°=36°,
故答案为:36.
一十六.全等三角形的判定(共1小题)
24.(2021春 奉贤区期末)如图,已知AC=DC,∠1=∠2,请添加一个条件,使△ABC≌△DEC,这个条件可以是 BC=EC .
【解答】解:添加BC=EC,
∵∠1=∠2,
∴∠1+∠ACD=∠2+∠ACD,
即∠ACB=∠ECD,
在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),
故答案为:BC=EC.
一.科学记数法与有效数字(共2小题)
1.(2021春 杨浦区期末)据第七次全国人口普查发布的数据显示,2020年上海市总人口约为24870000人,将24870000这个数保留两个有效数字并用科学记数法表示是 .
2.(2022 天山区校级二模)月球沿着一定的轨道围绕地球运动,某一时刻它与地球相距405 500千米,用科学记数法表示这个数并保留三个有效数字 .
二.平方根(共1小题)
3.(2021春 杨浦区期末)如果x2=25,则x= .
三.立方根(共1小题)
4.(2021春 静安区期末)已知a3=216,那么a= .
四.实数的运算(共1小题)
5.(2021 沙坪坝区校级模拟)计算:﹣|﹣3|= .
五.分数指数幂(共3小题)
6.(2021春 静安区期末)计算:4= .
7.(2021春 黄浦区期末)把表示成幂的形式是 .
8.(2021春 嘉定区期末)把表示成幂的形式是 .
六.二次根式的乘除法(共1小题)
9.(2021春 杨浦区期末)计算:= .
七.分母有理化(共1小题)
10.(2021春 奉贤区期末)计算:= .
八.二次根式的混合运算(共1小题)
11.(2021春 黄浦区期末)计算:(3+)2×(3﹣)2= .
九.点的坐标(共2小题)
12.(2021春 奉贤区期末)已知点P位于第四象限内,且点P到x轴的距离是2,到y轴的距离是4,则点P的坐标为 .
13.(2021春 静安区期末)在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 .
一十.坐标与图形性质(共2小题)
14.(2021春 奉贤区期末)经过点M(3,1)且平行于x轴的直线可以表示为直线 .
15.(2021春 浦东新区期末)在平面直角坐标系中,线段AB=3,且AB∥x轴,如果点A的坐标为(﹣1,2),那么点B的坐标是 .
一十一.平行线的性质(共2小题)
16.(2021春 金坛区期末)若∠A与∠B的一组边平行,另一组边垂直,且∠A﹣2∠B=15°,则∠B的度数为 .
17.(2021春 嘉定区期末)如图,直线a∥b且直线c与a、b相交,若∠1=70°,则∠2= °.
一十二.三角形的面积(共3小题)
18.(2021春 杨浦区期末)如图,在△ABC中,AB=AD=DC,AE⊥BD,如果△ABC的面积是12,那么△ABE的面积是 .
19.(2021春 静安区校级期末)如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t= ,△APE的面积等于6.
20.(2015春 崇明区期末)如图,l1∥l2,点A、E在直线l1上,点B、C、D在直线l2上,如果BD:CD=2:1,△ABC的面积为30,那么△BDE的面积是 .
一十三.三角形三边关系(共1小题)
21.(2021春 杨浦区期末)如果三角形的三条边长分别为2、x、6,那么x的取值范围是 .
一十四.三角形内角和定理(共1小题)
22.(2021春 黄浦区期末)在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是 三角形.
一十五.全等三角形的性质(共1小题)
23.(2021春 浦东新区期末)如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 °.
一十六.全等三角形的判定(共1小题)
24.(2021春 奉贤区期末)如图,已知AC=DC,∠1=∠2,请添加一个条件,使△ABC≌△DEC,这个条件可以是 .
参考答案与试题解析
一.科学记数法与有效数字(共2小题)
1.(2021春 杨浦区期末)据第七次全国人口普查发布的数据显示,2020年上海市总人口约为24870000人,将24870000这个数保留两个有效数字并用科学记数法表示是 2.5×107 .
【解答】解:24870000=2.487×107≈2.5×107.
故答案是:2.5×107.
2.(2022 天山区校级二模)月球沿着一定的轨道围绕地球运动,某一时刻它与地球相距405 500千米,用科学记数法表示这个数并保留三个有效数字 4.06×105 .
【解答】解:405 500千米=4.055×105千米≈4.06×105千米.
故答案为4.06×105.
二.平方根(共1小题)
3.(2021春 杨浦区期末)如果x2=25,则x= ±5 .
【解答】解:∵x2=25,
∴x=±5,
故答案为:±5.
三.立方根(共1小题)
4.(2021春 静安区期末)已知a3=216,那么a= 6 .
【解答】解:因为a3=216,
所以a==6.
故答案为:6.
四.实数的运算(共1小题)
5.(2021 沙坪坝区校级模拟)计算:﹣|﹣3|= ﹣5 .
【解答】解:﹣|﹣3|
=﹣2﹣3
=﹣5.
故答案为:﹣5.
五.分数指数幂(共3小题)
6.(2021春 静安区期末)计算:4= .
【解答】解:因为4=22,所以
7.(2021春 黄浦区期末)把表示成幂的形式是 .
【解答】解:把表示成幂的形式是.
故答案为.
8.(2021春 嘉定区期末)把表示成幂的形式是 .
【解答】解:
故答案为:.
六.二次根式的乘除法(共1小题)
9.(2021春 杨浦区期末)计算:= .
【解答】解:
=
=.
故答案为:.
七.分母有理化(共1小题)
10.(2021春 奉贤区期末)计算:= 2 .
【解答】解:原式=×
=
=2,
故答案为:2.
八.二次根式的混合运算(共1小题)
11.(2021春 黄浦区期末)计算:(3+)2×(3﹣)2= 49 .
【解答】解:(3+)2×(3﹣)2
=[(3+)×(3﹣)]2
=[]2
=72
=49.
故答案为:49.
九.点的坐标(共2小题)
12.(2021春 奉贤区期末)已知点P位于第四象限内,且点P到x轴的距离是2,到y轴的距离是4,则点P的坐标为 (4,﹣2) .
【解答】解:因为点P在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点P到x轴和y轴的距离分别是2和4,
所以点P的坐标为(4,﹣2).
故答案为(4,﹣2).
13.(2021春 静安区期末)在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 ﹣1或0 .
【解答】解:∵格点P(2m﹣1,m+2)在第二象限,
∴,
解不等式①得,m<,
解不等式②得,m>﹣2,
∴不等式的解集为﹣2<m<,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为﹣1或0.
故答案为:﹣1或0.
一十.坐标与图形性质(共2小题)
14.(2021春 奉贤区期末)经过点M(3,1)且平行于x轴的直线可以表示为直线 y=1 .
【解答】解:∵所求直线经过点M(3,1)且平行于x轴,
∴该直线上所有点纵坐标都是1,
故可以表示为直线y=1.
故答案为:y=1.
15.(2021春 浦东新区期末)在平面直角坐标系中,线段AB=3,且AB∥x轴,如果点A的坐标为(﹣1,2),那么点B的坐标是 (﹣4,2),(2,2) .
【解答】解:∵AB∥x轴且A(﹣1,2),
∴点B的纵坐标为2,
又∵AB=3,
∴点B的横坐标为﹣1+3=2或﹣1﹣3=﹣4,
∴点B的坐标为(2,2)或(﹣4,2),
故答案为:(﹣4,2),(2,2).
一十一.平行线的性质(共2小题)
16.(2021春 金坛区期末)若∠A与∠B的一组边平行,另一组边垂直,且∠A﹣2∠B=15°,则∠B的度数为 75°或25° .
【解答】解:如图1:
∵AE∥BF,
∴∠A+∠1=180°,
∴∠1=180°﹣∠A,
∵∠A﹣2∠B=15°,
∴∠1=180°﹣(2∠B+15°)=165°﹣2∠B,
∵AC⊥BC,
∴∠1+∠B=90°,
∴165°﹣2∠B+∠B=90°,
∴∠B=75°;
如图2:
∵AE∥BF,
∴∠A=∠1,
∵∠A﹣2∠B=15°,
∴∠1=2∠B+15°,
∵AC⊥BC,
∴∠1+∠B=90°,
∴2∠B+15°+∠B=90°,
∴∠B=25°;
综上,∠B的度数为75°或25°.
故答案为:75°或25°.
17.(2021春 嘉定区期末)如图,直线a∥b且直线c与a、b相交,若∠1=70°,则∠2= 110 °.
【解答】解:如图,
∵a∥b,
∴∠1=∠3,
∵∠1=70°,
∴∠3=70°,
∴∠2=180°﹣∠3=110°,
故答案为110.
一十二.三角形的面积(共3小题)
18.(2021春 杨浦区期末)如图,在△ABC中,AB=AD=DC,AE⊥BD,如果△ABC的面积是12,那么△ABE的面积是 3 .
【解答】解:∵AB=AD=AC,
∴D是△ABC的中线,
∴S△ABD=S△ABC=12=6,
∵△ABD是等腰三角形,AE⊥BD,
∴点E是BD的中点,
∴S△ABE=S△ABD=6=3.
故答案为:3.
19.(2021春 静安区校级期末)如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t= 1.5s或5s或9s ,△APE的面积等于6.
【解答】解:如图1,当点P在AC上,
∵△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,
∴CE=4,AP=2t.
∵△APE的面积等于6,
∴S△APE=AP CE=×2t×4=6,
∴t=1.5;
如图2,当点P在线段CE上,
∵E是DC的中点,
∴BE=CE=4.
∴PE=4﹣(t﹣3)=7﹣t,
∴S=EP AC= (7﹣t)×6=6,
∴t=5,
如图3,当P在线段BE上,
同理:PE=t﹣3﹣4=t﹣7,
∴S=EP AC= (t﹣7)×6=6,
∴t=9,
综上所述,t的值为1.5或5或9;
故答案为:1.5或5或9.
20.(2015春 崇明区期末)如图,l1∥l2,点A、E在直线l1上,点B、C、D在直线l2上,如果BD:CD=2:1,△ABC的面积为30,那么△BDE的面积是 20 .
【解答】解:∵l1∥l2,
∴△BDE的面积:△ABC的面积=BD:BC=2:3,
∴△BDE的面积=30×=20.
故答案为:20.
一十三.三角形三边关系(共1小题)
21.(2021春 杨浦区期末)如果三角形的三条边长分别为2、x、6,那么x的取值范围是 4<x<8 .
【解答】解:根据题意得:6﹣2<x<6+2,
即4<x<8.
故答案为:4<x<8.
一十四.三角形内角和定理(共1小题)
22.(2021春 黄浦区期末)在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是 等腰直角 三角形.
【解答】解:设一份为k°,则三个内角的度数分别为k°,k°,2k°.
则k°+k°+2k°=180°,
解得k°=45°.
∴2k°=90°,
所以这个三角形是等腰直角三角形.
故应填:等腰直角.
一十五.全等三角形的性质(共1小题)
23.(2021春 浦东新区期末)如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 36 °.
【解答】解:∵△ABC≌△ADE,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠BAD=40°,
∴∠ABD=∠ADB=(180°﹣∠BAD)=70°,
∵△ABC≌△ADE,
∴∠ADE=∠ABD=70°,
∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=114°﹣40°=74°,
∴∠E=180°﹣∠ADE﹣∠DAE=180°﹣70°﹣74°=36°,
故答案为:36.
一十六.全等三角形的判定(共1小题)
24.(2021春 奉贤区期末)如图,已知AC=DC,∠1=∠2,请添加一个条件,使△ABC≌△DEC,这个条件可以是 BC=EC .
【解答】解:添加BC=EC,
∵∠1=∠2,
∴∠1+∠ACD=∠2+∠ACD,
即∠ACB=∠ECD,
在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),
故答案为:BC=EC.
同课章节目录
