06填空题(基础提升题)(含解析)-2021年春上海市各区七年级(下)期末数学知识点分类汇编
文档属性
| 名称 | 06填空题(基础提升题)(含解析)-2021年春上海市各区七年级(下)期末数学知识点分类汇编 |

|
|
| 格式 | doc | ||
| 文件大小 | 265.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 08:51:41 | ||
图片预览



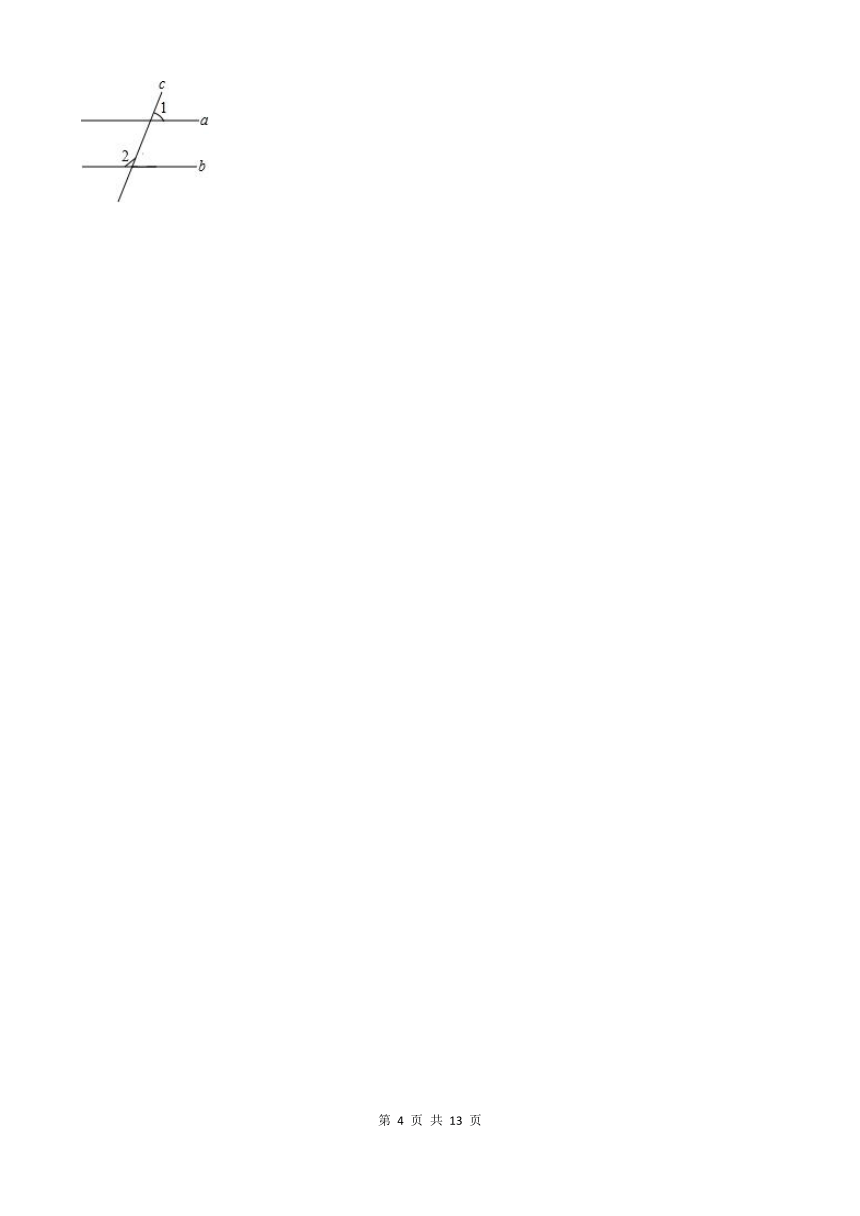

文档简介
06填空题(基础提升题)
一.近似数和有效数字(共2小题)
1.(2021春 静安区校级期末)近似数2.60×105精确到 位.
2.(2021春 静安区校级期末)用科学记数法表示2021(保留两个有效数字),结果是 .
二.科学记数法与有效数字(共2小题)
3.(2021春 嘉定区期末)据第7次全国人口普查统计,截止2020年11月1日零时,全国人口共141178万人,将141178这个数保留四个有效数字并用科学记数法表示是 .
4.(2021春 金山区期末)截止2021年5月16日,全球累计新冠肺炎死亡病例3352109例,将3352109用科学记数法表示,并保留3个有效数字,应记为 .
三.算术平方根(共1小题)
5.(2021春 闵行区期末)计算:= .
四.立方根(共2小题)
6.(2021春 静安区校级期末)把化成幂的形式 .
7.(2021春 静安区期末)已知a3=216,那么a= .
五.实数与数轴(共2小题)
8.(2021春 静安区校级期末)在数轴上,点A、点B对应的数分别是和,则AB= .
9.(2021春 闵行区期末)点A和点B是数轴上的两点,点A表示的数为,点B表示的数为1,那么A、B两点间的距离为 .
六.实数大小比较(共2小题)
10.(2021春 嘉定区期末)比较大小:3.14 (填“>”、“=”或“<”).
11.(2021春 闵行区期末)比较大小:3 5.
七.估算无理数的大小(共1小题)
12.(2021春 浦东新区校级期末)数轴上表示数和的两点之间的距离为 .
八.分数指数幂(共2小题)
13.(2021春 奉贤区期末)用幂的形式表示:= .
14.(2021春 静安区期末)计算:4= .
九.点的坐标(共3小题)
15.(2021春 松江区期末)若点P(3,m﹣2)在x轴上,则点Q(m﹣3,m+1)在第 象限.
16.(2021春 松江区期末)已知点A在直线x=﹣3上,到x轴的距离为5,且点A在第三象限,则点A的坐标为 .
17.(2021春 静安区期末)在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 .
一十.坐标与图形性质(共3小题)
18.(2021春 静安区校级期末)在平面坐标系中,点P(﹣2,1),B(3,1),则PB= .
19.(2021春 静安区校级期末)在平面直角坐标系中,如果过点A(1,2)和点B的直线平行于x轴,且AB=3,那么点B的坐标是 .
20.(2021春 浦东新区校级期末)已知点P(3m﹣6,m+1),A(﹣1,2),直线PA与x轴平行,则点P的坐标为 .
一十一.对顶角、邻补角(共1小题)
21.(2021春 静安区校级期末)如图,直线AB与CD相交于点O,∠AOD=120°,直线AB与CD的夹角的度数是 度.
一十二.点到直线的距离(共1小题)
22.(2021春 浦东新区期末)如图,点A到直线BC的距离是线段 的长度.
一十三.平行线的性质(共7小题)
23.(2021春 静安区校级期末)将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2= .
24.(2021春 静安区校级期末)如图,AD∥BC,BD平分∠ABC,且∠A=2∠ABC,∠DBC= 度.
25.(2021春 金山区期末)如图,已知DE∥BC,∠ABC=70°,那么直线AB与直线DE的夹角等于 .
26.(2021春 金山区期末)如图,在直线l1∥l2,把三角板的直角顶点放在直线l2上,三角板中60°的角在直线l1与l2之间,如果∠1=35°,那么∠2= °.
27.(2021春 闵行区期末)如图,已知AB∥CD,直线EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=30°,那么∠EFP的度数为 .
28.(2020 武昌区模拟)如图,AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=40°,那么∠BED的度数为 .
29.(2021春 奉贤区期末)已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x﹣5)°,那么∠1= °.
参考答案与试题解析
一.近似数和有效数字(共2小题)
1.(2021春 静安区校级期末)近似数2.60×105精确到 千 位.
【解答】解:2.60×105=260000,6后面0在千位上,所以2.60×105精确到千位.
故答案是:千.
2.(2021春 静安区校级期末)用科学记数法表示2021(保留两个有效数字),结果是 2.0×103 .
【解答】解:数字2021用科学记数法表示并保留两个有效数字为:2021≈2.0×103.
故答案为:2.0×103.
二.科学记数法与有效数字(共2小题)
3.(2021春 嘉定区期末)据第7次全国人口普查统计,截止2020年11月1日零时,全国人口共141178万人,将141178这个数保留四个有效数字并用科学记数法表示是 1.412×105 .
【解答】解:将141178用科学记数法表示是1.41178×105,
再将这个数保留四个有效数字为1.412×105,
故答案为:1.412×105.
4.(2021春 金山区期末)截止2021年5月16日,全球累计新冠肺炎死亡病例3352109例,将3352109用科学记数法表示,并保留3个有效数字,应记为 3.35×106 .
【解答】解:3352109这个数字用科学记数法并保留3个有效数字表示为3.35×106.
故答案为:3.35×106.
三.算术平方根(共1小题)
5.(2021春 闵行区期末)计算:= 10 .
【解答】解:===10.
故答案为:10.
四.立方根(共2小题)
6.(2021春 静安区校级期末)把化成幂的形式 .
【解答】解:由=,可得=,
故答案为:.
7.(2021春 静安区期末)已知a3=216,那么a= 6 .
【解答】解:因为a3=216,
所以a==6.
故答案为:6.
五.实数与数轴(共2小题)
8.(2021春 静安区校级期末)在数轴上,点A、点B对应的数分别是和,则AB= 3 .
【解答】解:∵点A、点B对应的数分别是和,∴.
故答案为:.
9.(2021春 闵行区期末)点A和点B是数轴上的两点,点A表示的数为,点B表示的数为1,那么A、B两点间的距离为 ﹣1 .
【解答】解:如图,
∵A表示的数为,点B表示的数为1,
∴OA=,OB=1.
∴AB=OA﹣OB=.
故答案为:.
六.实数大小比较(共2小题)
10.(2021春 嘉定区期末)比较大小:3.14 < (填“>”、“=”或“<”).
【解答】解:∵3.142=9.8596,()2=10,
∴3.142<()2,
∴3.14<,
故答案为:<.
11.(2021春 闵行区期末)比较大小:3 < 5.
【解答】解:∵(3)2=45,(5)2=75,
∴3<5.
故填空答案:<.
七.估算无理数的大小(共1小题)
12.(2021春 浦东新区校级期末)数轴上表示数和的两点之间的距离为 .
【解答】解:﹣(﹣5)
=+5
=,
故答案为:.
八.分数指数幂(共2小题)
13.(2021春 奉贤区期末)用幂的形式表示:= 7 .
【解答】解:原式=7,
故答案为:7.
14.(2021春 静安区期末)计算:4= .
【解答】解:因为4=22,所以
九.点的坐标(共3小题)
15.(2021春 松江区期末)若点P(3,m﹣2)在x轴上,则点Q(m﹣3,m+1)在第 二 象限.
【解答】解:由题意,得m﹣2=0,
∴m=2.
∴m﹣3=﹣1<0,m+1=3>0,
∴点Q(m﹣3,m+1)在二象限,
故答案为:二.
16.(2021春 松江区期末)已知点A在直线x=﹣3上,到x轴的距离为5,且点A在第三象限,则点A的坐标为 (﹣3,﹣5) .
【解答】解:∵点A在第三象限内,点A到x轴的距离是5,点A在直线x=﹣3上,
∴点A的横坐标为﹣3,纵坐标为﹣5,
∴点A的坐标为(﹣3,﹣5).
故答案为:(﹣3,﹣5).
17.(2021春 静安区期末)在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 ﹣1或0 .
【解答】解:∵格点P(2m﹣1,m+2)在第二象限,
∴,
解不等式①得,m<,
解不等式②得,m>﹣2,
∴不等式的解集为﹣2<m<,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为﹣1或0.
故答案为:﹣1或0.
一十.坐标与图形性质(共3小题)
18.(2021春 静安区校级期末)在平面坐标系中,点P(﹣2,1),B(3,1),则PB= 5 .
【解答】解:∵P(﹣2,1),B(3,1),
∴PB=3﹣(﹣2)=5,
故答案为:5.
19.(2021春 静安区校级期末)在平面直角坐标系中,如果过点A(1,2)和点B的直线平行于x轴,且AB=3,那么点B的坐标是 (﹣2,2)或(4,2) .
【解答】解:∵AB所在直线平行于x轴,点A的坐标为(1,2),
∴点B的纵坐标为2.
①当点B在点A的左边时,
∵点B到点A的距离为3,
∴点B的横坐标为1﹣3=﹣2.
∴点B的坐标为(﹣2,2).
②当点B在点A的右边时,
∵点B到点A的距离为3,
∴点B的横坐标为1+3=4.
∴点B的坐标为(4,2),
∴点B的坐标为(﹣2,2)或(4,2).
故答案为(﹣2,2)或(4,2).
20.(2021春 浦东新区校级期末)已知点P(3m﹣6,m+1),A(﹣1,2),直线PA与x轴平行,则点P的坐标为 (﹣3,2) .
【解答】解:∵点P(3m﹣6,m+1)在过点A(﹣1,2)且与x轴平行的直线上,
∴m+1=2,
解得m=1,
∴3m﹣6=3×1﹣6=﹣3,
∴m+1=1+1=2,
∴点P的坐标为(﹣3,2),
故答案为:(﹣3,2).
一十一.对顶角、邻补角(共1小题)
21.(2021春 静安区校级期末)如图,直线AB与CD相交于点O,∠AOD=120°,直线AB与CD的夹角的度数是 60 度.
【解答】解:∵∠AOD+∠BOD=180°,
∴∠BOD=180°﹣∠AOD
=180°﹣120°=60°.
故答案为:60.
一十二.点到直线的距离(共1小题)
22.(2021春 浦东新区期末)如图,点A到直线BC的距离是线段 AE 的长度.
【解答】解:∵AE⊥BC,垂足为E,
∴点A到直线BC的距离是线段AE的长度.
故答案为:AE.
一十三.平行线的性质(共7小题)
23.(2021春 静安区校级期末)将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2= 90° .
【解答】证明:如图,过点B作BN∥FG,
∵四边形EFGH是矩形纸片,
∴EH∥FG,
∴BN∥EH∥FG,
∴∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4=∠ABC=90°,
即∠1+∠2=90°.
故答案为:90°.
24.(2021春 静安区校级期末)如图,AD∥BC,BD平分∠ABC,且∠A=2∠ABC,∠DBC= 30 度.
【解答】解:∵AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=2∠ABC,
∴3∠ABC=180°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴.
故答案为:30.
25.(2021春 金山区期末)如图,已知DE∥BC,∠ABC=70°,那么直线AB与直线DE的夹角等于 70° .
【解答】解:如图,直线AB和DE相交于点F,
∵BC∥DE,∠ABC=70°,
∴∠AFE=∠ABC=70°,
∴直线AB、DE的夹角是70°.
故答案为:70°.
26.(2021春 金山区期末)如图,在直线l1∥l2,把三角板的直角顶点放在直线l2上,三角板中60°的角在直线l1与l2之间,如果∠1=35°,那么∠2= 65 °.
【解答】解:∵∠3是△ABC的外角,∠1=∠ABC=35°,
∴∠3=∠C+∠ABC=30°+35°=65°,
∵直线l1∥l2,
∴∠2=∠3=65°,
故答案为:65.
27.(2021春 闵行区期末)如图,已知AB∥CD,直线EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=30°,那么∠EFP的度数为 30° .
【解答】解:∵EP⊥EF,
∴∠FEP=90°.
∴∠FEB=∠FEP+∠BEP=120°.
∵AB∥CD,
∴∠BEF+∠EFD=180°.
∴∠EFD=180°﹣∠BEF=180°﹣120°=60°.
又∵PF平分∠EFD,
∴∠EFP=.
故答案为:30°.
28.(2020 武昌区模拟)如图,AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=40°,那么∠BED的度数为 130° .
【解答】解:∵AE平分∠BAC,
∴∠BAE=∠CAE=40°,
∵ED∥AC,
∴∠CAE+∠DEA=180°,
∴∠DEA=180°﹣40°=140°,
∵∠AED+∠AEB+∠BED=360°,
∴∠BED=360°﹣140°﹣90°=130°.
故答案为:130°.
29.(2021春 奉贤区期末)已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x﹣5)°,那么∠1= 80 °.
【解答】解:∵直线a∥b,
∴∠1=∠3,
∵∠2+∠3=180°,
∴∠1+∠2=180°,
∵∠1=(2x+10)°,∠2=(3x﹣5)°,
∴2x+10+3x﹣5=180,
解得:x=35,
∴∠1=80°.
故答案为:80.
一.近似数和有效数字(共2小题)
1.(2021春 静安区校级期末)近似数2.60×105精确到 位.
2.(2021春 静安区校级期末)用科学记数法表示2021(保留两个有效数字),结果是 .
二.科学记数法与有效数字(共2小题)
3.(2021春 嘉定区期末)据第7次全国人口普查统计,截止2020年11月1日零时,全国人口共141178万人,将141178这个数保留四个有效数字并用科学记数法表示是 .
4.(2021春 金山区期末)截止2021年5月16日,全球累计新冠肺炎死亡病例3352109例,将3352109用科学记数法表示,并保留3个有效数字,应记为 .
三.算术平方根(共1小题)
5.(2021春 闵行区期末)计算:= .
四.立方根(共2小题)
6.(2021春 静安区校级期末)把化成幂的形式 .
7.(2021春 静安区期末)已知a3=216,那么a= .
五.实数与数轴(共2小题)
8.(2021春 静安区校级期末)在数轴上,点A、点B对应的数分别是和,则AB= .
9.(2021春 闵行区期末)点A和点B是数轴上的两点,点A表示的数为,点B表示的数为1,那么A、B两点间的距离为 .
六.实数大小比较(共2小题)
10.(2021春 嘉定区期末)比较大小:3.14 (填“>”、“=”或“<”).
11.(2021春 闵行区期末)比较大小:3 5.
七.估算无理数的大小(共1小题)
12.(2021春 浦东新区校级期末)数轴上表示数和的两点之间的距离为 .
八.分数指数幂(共2小题)
13.(2021春 奉贤区期末)用幂的形式表示:= .
14.(2021春 静安区期末)计算:4= .
九.点的坐标(共3小题)
15.(2021春 松江区期末)若点P(3,m﹣2)在x轴上,则点Q(m﹣3,m+1)在第 象限.
16.(2021春 松江区期末)已知点A在直线x=﹣3上,到x轴的距离为5,且点A在第三象限,则点A的坐标为 .
17.(2021春 静安区期末)在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 .
一十.坐标与图形性质(共3小题)
18.(2021春 静安区校级期末)在平面坐标系中,点P(﹣2,1),B(3,1),则PB= .
19.(2021春 静安区校级期末)在平面直角坐标系中,如果过点A(1,2)和点B的直线平行于x轴,且AB=3,那么点B的坐标是 .
20.(2021春 浦东新区校级期末)已知点P(3m﹣6,m+1),A(﹣1,2),直线PA与x轴平行,则点P的坐标为 .
一十一.对顶角、邻补角(共1小题)
21.(2021春 静安区校级期末)如图,直线AB与CD相交于点O,∠AOD=120°,直线AB与CD的夹角的度数是 度.
一十二.点到直线的距离(共1小题)
22.(2021春 浦东新区期末)如图,点A到直线BC的距离是线段 的长度.
一十三.平行线的性质(共7小题)
23.(2021春 静安区校级期末)将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2= .
24.(2021春 静安区校级期末)如图,AD∥BC,BD平分∠ABC,且∠A=2∠ABC,∠DBC= 度.
25.(2021春 金山区期末)如图,已知DE∥BC,∠ABC=70°,那么直线AB与直线DE的夹角等于 .
26.(2021春 金山区期末)如图,在直线l1∥l2,把三角板的直角顶点放在直线l2上,三角板中60°的角在直线l1与l2之间,如果∠1=35°,那么∠2= °.
27.(2021春 闵行区期末)如图,已知AB∥CD,直线EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=30°,那么∠EFP的度数为 .
28.(2020 武昌区模拟)如图,AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=40°,那么∠BED的度数为 .
29.(2021春 奉贤区期末)已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x﹣5)°,那么∠1= °.
参考答案与试题解析
一.近似数和有效数字(共2小题)
1.(2021春 静安区校级期末)近似数2.60×105精确到 千 位.
【解答】解:2.60×105=260000,6后面0在千位上,所以2.60×105精确到千位.
故答案是:千.
2.(2021春 静安区校级期末)用科学记数法表示2021(保留两个有效数字),结果是 2.0×103 .
【解答】解:数字2021用科学记数法表示并保留两个有效数字为:2021≈2.0×103.
故答案为:2.0×103.
二.科学记数法与有效数字(共2小题)
3.(2021春 嘉定区期末)据第7次全国人口普查统计,截止2020年11月1日零时,全国人口共141178万人,将141178这个数保留四个有效数字并用科学记数法表示是 1.412×105 .
【解答】解:将141178用科学记数法表示是1.41178×105,
再将这个数保留四个有效数字为1.412×105,
故答案为:1.412×105.
4.(2021春 金山区期末)截止2021年5月16日,全球累计新冠肺炎死亡病例3352109例,将3352109用科学记数法表示,并保留3个有效数字,应记为 3.35×106 .
【解答】解:3352109这个数字用科学记数法并保留3个有效数字表示为3.35×106.
故答案为:3.35×106.
三.算术平方根(共1小题)
5.(2021春 闵行区期末)计算:= 10 .
【解答】解:===10.
故答案为:10.
四.立方根(共2小题)
6.(2021春 静安区校级期末)把化成幂的形式 .
【解答】解:由=,可得=,
故答案为:.
7.(2021春 静安区期末)已知a3=216,那么a= 6 .
【解答】解:因为a3=216,
所以a==6.
故答案为:6.
五.实数与数轴(共2小题)
8.(2021春 静安区校级期末)在数轴上,点A、点B对应的数分别是和,则AB= 3 .
【解答】解:∵点A、点B对应的数分别是和,∴.
故答案为:.
9.(2021春 闵行区期末)点A和点B是数轴上的两点,点A表示的数为,点B表示的数为1,那么A、B两点间的距离为 ﹣1 .
【解答】解:如图,
∵A表示的数为,点B表示的数为1,
∴OA=,OB=1.
∴AB=OA﹣OB=.
故答案为:.
六.实数大小比较(共2小题)
10.(2021春 嘉定区期末)比较大小:3.14 < (填“>”、“=”或“<”).
【解答】解:∵3.142=9.8596,()2=10,
∴3.142<()2,
∴3.14<,
故答案为:<.
11.(2021春 闵行区期末)比较大小:3 < 5.
【解答】解:∵(3)2=45,(5)2=75,
∴3<5.
故填空答案:<.
七.估算无理数的大小(共1小题)
12.(2021春 浦东新区校级期末)数轴上表示数和的两点之间的距离为 .
【解答】解:﹣(﹣5)
=+5
=,
故答案为:.
八.分数指数幂(共2小题)
13.(2021春 奉贤区期末)用幂的形式表示:= 7 .
【解答】解:原式=7,
故答案为:7.
14.(2021春 静安区期末)计算:4= .
【解答】解:因为4=22,所以
九.点的坐标(共3小题)
15.(2021春 松江区期末)若点P(3,m﹣2)在x轴上,则点Q(m﹣3,m+1)在第 二 象限.
【解答】解:由题意,得m﹣2=0,
∴m=2.
∴m﹣3=﹣1<0,m+1=3>0,
∴点Q(m﹣3,m+1)在二象限,
故答案为:二.
16.(2021春 松江区期末)已知点A在直线x=﹣3上,到x轴的距离为5,且点A在第三象限,则点A的坐标为 (﹣3,﹣5) .
【解答】解:∵点A在第三象限内,点A到x轴的距离是5,点A在直线x=﹣3上,
∴点A的横坐标为﹣3,纵坐标为﹣5,
∴点A的坐标为(﹣3,﹣5).
故答案为:(﹣3,﹣5).
17.(2021春 静安区期末)在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 ﹣1或0 .
【解答】解:∵格点P(2m﹣1,m+2)在第二象限,
∴,
解不等式①得,m<,
解不等式②得,m>﹣2,
∴不等式的解集为﹣2<m<,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为﹣1或0.
故答案为:﹣1或0.
一十.坐标与图形性质(共3小题)
18.(2021春 静安区校级期末)在平面坐标系中,点P(﹣2,1),B(3,1),则PB= 5 .
【解答】解:∵P(﹣2,1),B(3,1),
∴PB=3﹣(﹣2)=5,
故答案为:5.
19.(2021春 静安区校级期末)在平面直角坐标系中,如果过点A(1,2)和点B的直线平行于x轴,且AB=3,那么点B的坐标是 (﹣2,2)或(4,2) .
【解答】解:∵AB所在直线平行于x轴,点A的坐标为(1,2),
∴点B的纵坐标为2.
①当点B在点A的左边时,
∵点B到点A的距离为3,
∴点B的横坐标为1﹣3=﹣2.
∴点B的坐标为(﹣2,2).
②当点B在点A的右边时,
∵点B到点A的距离为3,
∴点B的横坐标为1+3=4.
∴点B的坐标为(4,2),
∴点B的坐标为(﹣2,2)或(4,2).
故答案为(﹣2,2)或(4,2).
20.(2021春 浦东新区校级期末)已知点P(3m﹣6,m+1),A(﹣1,2),直线PA与x轴平行,则点P的坐标为 (﹣3,2) .
【解答】解:∵点P(3m﹣6,m+1)在过点A(﹣1,2)且与x轴平行的直线上,
∴m+1=2,
解得m=1,
∴3m﹣6=3×1﹣6=﹣3,
∴m+1=1+1=2,
∴点P的坐标为(﹣3,2),
故答案为:(﹣3,2).
一十一.对顶角、邻补角(共1小题)
21.(2021春 静安区校级期末)如图,直线AB与CD相交于点O,∠AOD=120°,直线AB与CD的夹角的度数是 60 度.
【解答】解:∵∠AOD+∠BOD=180°,
∴∠BOD=180°﹣∠AOD
=180°﹣120°=60°.
故答案为:60.
一十二.点到直线的距离(共1小题)
22.(2021春 浦东新区期末)如图,点A到直线BC的距离是线段 AE 的长度.
【解答】解:∵AE⊥BC,垂足为E,
∴点A到直线BC的距离是线段AE的长度.
故答案为:AE.
一十三.平行线的性质(共7小题)
23.(2021春 静安区校级期末)将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2= 90° .
【解答】证明:如图,过点B作BN∥FG,
∵四边形EFGH是矩形纸片,
∴EH∥FG,
∴BN∥EH∥FG,
∴∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4=∠ABC=90°,
即∠1+∠2=90°.
故答案为:90°.
24.(2021春 静安区校级期末)如图,AD∥BC,BD平分∠ABC,且∠A=2∠ABC,∠DBC= 30 度.
【解答】解:∵AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=2∠ABC,
∴3∠ABC=180°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴.
故答案为:30.
25.(2021春 金山区期末)如图,已知DE∥BC,∠ABC=70°,那么直线AB与直线DE的夹角等于 70° .
【解答】解:如图,直线AB和DE相交于点F,
∵BC∥DE,∠ABC=70°,
∴∠AFE=∠ABC=70°,
∴直线AB、DE的夹角是70°.
故答案为:70°.
26.(2021春 金山区期末)如图,在直线l1∥l2,把三角板的直角顶点放在直线l2上,三角板中60°的角在直线l1与l2之间,如果∠1=35°,那么∠2= 65 °.
【解答】解:∵∠3是△ABC的外角,∠1=∠ABC=35°,
∴∠3=∠C+∠ABC=30°+35°=65°,
∵直线l1∥l2,
∴∠2=∠3=65°,
故答案为:65.
27.(2021春 闵行区期末)如图,已知AB∥CD,直线EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=30°,那么∠EFP的度数为 30° .
【解答】解:∵EP⊥EF,
∴∠FEP=90°.
∴∠FEB=∠FEP+∠BEP=120°.
∵AB∥CD,
∴∠BEF+∠EFD=180°.
∴∠EFD=180°﹣∠BEF=180°﹣120°=60°.
又∵PF平分∠EFD,
∴∠EFP=.
故答案为:30°.
28.(2020 武昌区模拟)如图,AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=40°,那么∠BED的度数为 130° .
【解答】解:∵AE平分∠BAC,
∴∠BAE=∠CAE=40°,
∵ED∥AC,
∴∠CAE+∠DEA=180°,
∴∠DEA=180°﹣40°=140°,
∵∠AED+∠AEB+∠BED=360°,
∴∠BED=360°﹣140°﹣90°=130°.
故答案为:130°.
29.(2021春 奉贤区期末)已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x﹣5)°,那么∠1= 80 °.
【解答】解:∵直线a∥b,
∴∠1=∠3,
∵∠2+∠3=180°,
∴∠1+∠2=180°,
∵∠1=(2x+10)°,∠2=(3x﹣5)°,
∴2x+10+3x﹣5=180,
解得:x=35,
∴∠1=80°.
故答案为:80.
同课章节目录
