05填空题(基础题)2021年春上海市各区七年级(下)期末数学知识点分类汇编
文档属性
| 名称 | 05填空题(基础题)2021年春上海市各区七年级(下)期末数学知识点分类汇编 |

|
|
| 格式 | docx | ||
| 文件大小 | 146.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 20:33:30 | ||
图片预览


文档简介
05填空题(基础题)
一十一.零指数幂(共1小题)
32.(2022 漳州模拟)计算:20= .
一十二.二次根式的乘除法(共1小题)
33.(2021春 浦东新区期末)计算:×= .
一十三.点的坐标(共10小题)
34.(2021春 静安区校级期末)点A(﹣1,2)在第 象限.
35.(2021春 静安区校级期末)如果点A(2,t)在x轴上,那么点B(t﹣2,t+1)在第 象限.
36.(2021春 闵行区期末)在平面直角坐标系xOy中,已知点A(2,n)在第四象限,点B(m,1)在第二象限,那么点C(m,n)在第 象限.
37.(2021春 奉贤区期末)在平面直角坐标系中,经过点M(2,5)且垂直y轴的直线可以表示为直线 .
38.(2021春 奉贤区期末)在平面直角坐标系中,点P(6﹣a,4)到两坐标轴的距离相等,那么a的值是 .
39.(2021春 静安区期末)在平面直角坐标系中,经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线 .
40.(2021春 静安区期末)在平面直角坐标系中,如果点Q(a+1,2﹣a)在x轴上,那么a= .
41.(2021春 杨浦区期末)如果点P(x,y)在第四象限,那么点Q(2﹣y,x+1)在第 象限.
42.(2021春 杨浦区期末)在平面直角坐标系中,如果点M(a+1,2﹣a)在y轴上,那么点M的坐标是 .
43.(2021春 浦东新区期末)如果点M(a,b)在第二象限,那么点N(﹣a,b+1)在第 象限.
一十四.方向角(共1小题)
44.(2021春 闵行区期末)点A位于点B的北偏东方向15°,若将点B以点A为旋转中心旋转90°落在点C处,则点A在点C的 方向.
一十五.对顶角、邻补角(共1小题)
45.(2021春 静安区期末)如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 度.
一十六.垂线(共1小题)
46.(2021春 松江区期末)如图,直线AB,CD相交于O,OE平分∠AOC,OF⊥OE,若∠BOD=46°,则∠DOF的度数为 °.
一十七.平行线的性质(共1小题)
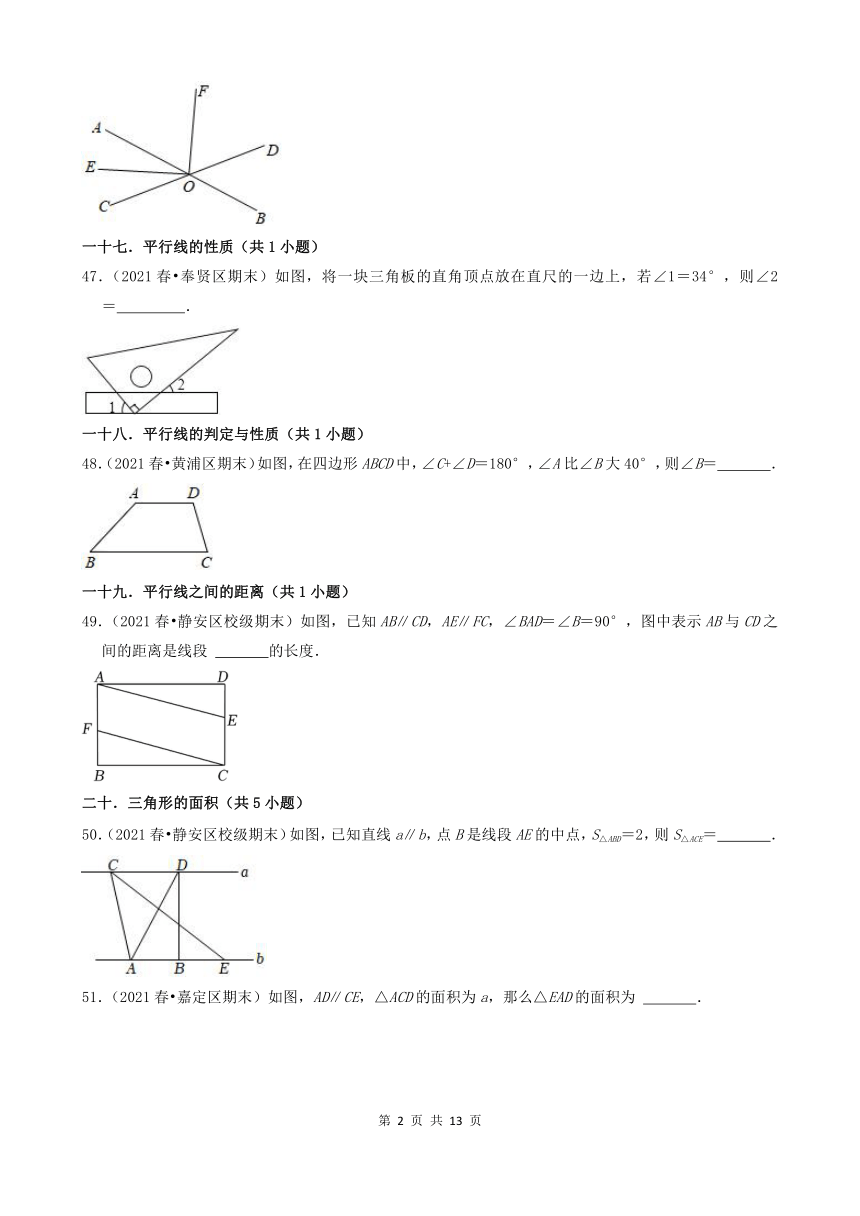
47.(2021春 奉贤区期末)如图,将一块三角板的直角顶点放在直尺的一边上,若∠1=34°,则∠2= .
一十八.平行线的判定与性质(共1小题)
48.(2021春 黄浦区期末)如图,在四边形ABCD中,∠C+∠D=180°,∠A比∠B大40°,则∠B= .
一十九.平行线之间的距离(共1小题)
49.(2021春 静安区校级期末)如图,已知AB∥CD,AE∥FC,∠BAD=∠B=90°,图中表示AB与CD之间的距离是线段 的长度.
二十.三角形的面积(共5小题)
50.(2021春 静安区校级期末)如图,已知直线a∥b,点B是线段AE的中点,S△ABD=2,则S△ACE= .
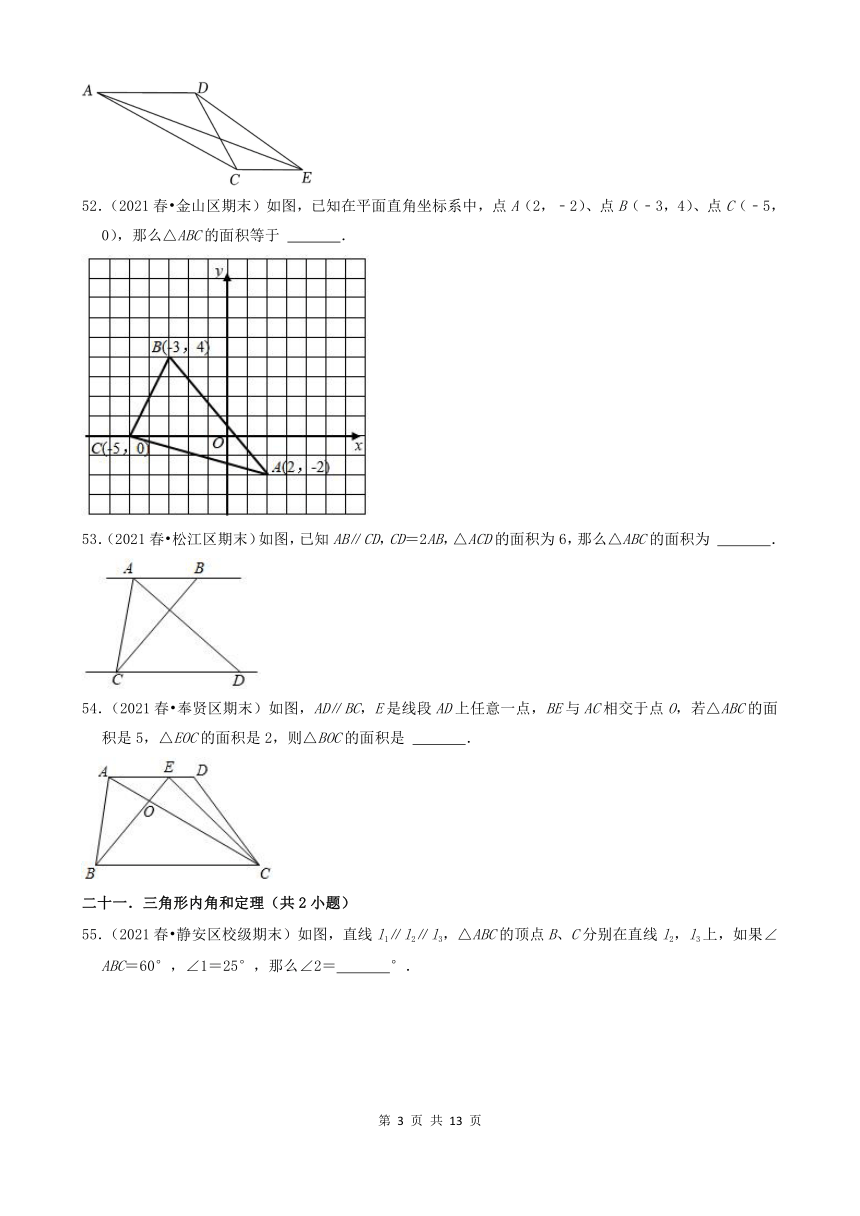
51.(2021春 嘉定区期末)如图,AD∥CE,△ACD的面积为a,那么△EAD的面积为 .
52.(2021春 金山区期末)如图,已知在平面直角坐标系中,点A(2,﹣2)、点B(﹣3,4)、点C(﹣5,0),那么△ABC的面积等于 .
53.(2021春 松江区期末)如图,已知AB∥CD,CD=2AB,△ACD的面积为6,那么△ABC的面积为 .
54.(2021春 奉贤区期末)如图,AD∥BC,E是线段AD上任意一点,BE与AC相交于点O,若△ABC的面积是5,△EOC的面积是2,则△BOC的面积是 .
二十一.三角形内角和定理(共2小题)
55.(2021春 静安区校级期末)如图,直线l1∥l2∥l3,△ABC的顶点B、C分别在直线l2,l3上,如果∠ABC=60°,∠1=25°,那么∠2= °.
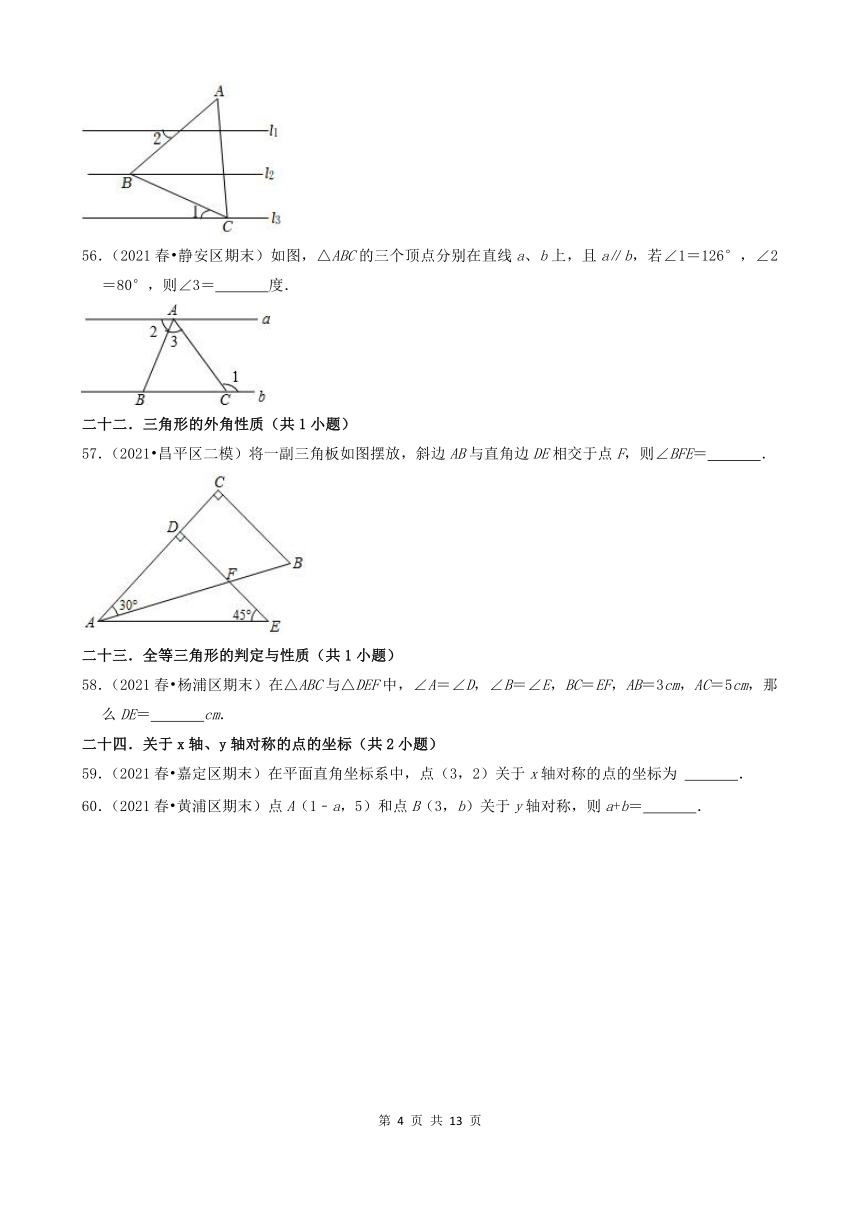
56.(2021春 静安区期末)如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 度.
二十二.三角形的外角性质(共1小题)
57.(2021 昌平区二模)将一副三角板如图摆放,斜边AB与直角边DE相交于点F,则∠BFE= .
二十三.全等三角形的判定与性质(共1小题)
58.(2021春 杨浦区期末)在△ABC与△DEF中,∠A=∠D,∠B=∠E,BC=EF,AB=3cm,AC=5cm,那么DE= cm.
二十四.关于x轴、y轴对称的点的坐标(共2小题)
59.(2021春 嘉定区期末)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 .
60.(2021春 黄浦区期末)点A(1﹣a,5)和点B(3,b)关于y轴对称,则a+b= .
参考答案与试题解析
一十一.零指数幂(共1小题)
32.(2022 漳州模拟)计算:20= 1 .
【解答】解:∵2≠0,
∴20=1.
故答案为:1.
一十二.二次根式的乘除法(共1小题)
33.(2021春 浦东新区期末)计算:×= 1 .
【解答】解:原式==1
故答案为:1
一十三.点的坐标(共10小题)
34.(2021春 静安区校级期末)点A(﹣1,2)在第 二 象限.
【解答】解:∵点A(﹣1,2)的横坐标小于零,纵坐标大于零,
∴点A(﹣1,2)在第二象限.
故答案为:二.
35.(2021春 静安区校级期末)如果点A(2,t)在x轴上,那么点B(t﹣2,t+1)在第 二 象限.
【解答】解:因为点A(2,t)在x轴上,
所以t=0,
则点B为(﹣2,1),
所以点B在第二象限.
故答案为:二.
36.(2021春 闵行区期末)在平面直角坐标系xOy中,已知点A(2,n)在第四象限,点B(m,1)在第二象限,那么点C(m,n)在第 三 象限.
【解答】解:∵点A(2,n)在第四象限,
∴n<0;
∵点B(m,1)在第二象限,
∴m<0,
∴点C(m,n)在第三象限.
故答案为:三.
37.(2021春 奉贤区期末)在平面直角坐标系中,经过点M(2,5)且垂直y轴的直线可以表示为直线 y=5 .
【解答】解:∵经过点M(2,5)且垂直于y轴,
∴直线可以表示为y=5.
故答案为:y=5.
38.(2021春 奉贤区期末)在平面直角坐标系中,点P(6﹣a,4)到两坐标轴的距离相等,那么a的值是 2或10 .
【解答】解:∵点P(6﹣a,4)到两坐标轴的距离相等,
∴|6﹣a|=4,
即6﹣a=4或6﹣a=﹣4,
解得a=2或a=10.
故答案为:2或10.
39.(2021春 静安区期末)在平面直角坐标系中,经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线 y=4 .
【解答】解:由题意得:经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线为:y=4,
故答案为:y=4.
40.(2021春 静安区期末)在平面直角坐标系中,如果点Q(a+1,2﹣a)在x轴上,那么a= 2 .
【解答】解:∵点Q(a+1,2﹣a)在x轴上,
∴2﹣a=0,
解得:a=2.
故答案为:2.
41.(2021春 杨浦区期末)如果点P(x,y)在第四象限,那么点Q(2﹣y,x+1)在第 一 象限.
【解答】解:∵点P(x,y)在第四象限,
∴x>0,y<0,
∴2﹣y>0,x+1>0,
∴Q(2﹣y,x+1)在第一象限.
故答案为:一.
42.(2021春 杨浦区期末)在平面直角坐标系中,如果点M(a+1,2﹣a)在y轴上,那么点M的坐标是 (0,3) .
【解答】解:∵M(a+1,2﹣a)在y轴上,
∴a+1=0,
解得a=﹣1,
∴2﹣a=2+1=3,
∴点M的坐标为(0,3).
故答案为:(0,3).
43.(2021春 浦东新区期末)如果点M(a,b)在第二象限,那么点N(﹣a,b+1)在第 一 象限.
【解答】解:∵点M(a,b)在第二象限,
∴a<0,b>0;
∴﹣a>0,b+1>1,
∴点N(﹣a,b+1)在第一象限.
故答案为:一.
一十四.方向角(共1小题)
44.(2021春 闵行区期末)点A位于点B的北偏东方向15°,若将点B以点A为旋转中心旋转90°落在点C处,则点A在点C的 北偏西75或南偏东75° 方向.
【解答】解:①若将点B以点A为旋转中心顺时针旋转90°落在点C处,则点A在点C的南偏东90°﹣15°=75°方向上,
②若将点B以点A为旋转中心逆时针旋转90°落在点C处,则点A在点C的北偏西90°﹣15°=75°方向上,
综上所述,点A在点C的北偏西75或南偏东75°方向,
故答案为:北偏西75或南偏东75°.
一十五.对顶角、邻补角(共1小题)
45.(2021春 静安区期末)如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 25 度.
【解答】解:∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD,
又∵∠ACO=∠BOD,
∴∠BOE=∠AOC=×50°=25°,
故答案为:25.
一十六.垂线(共1小题)
46.(2021春 松江区期末)如图,直线AB,CD相交于O,OE平分∠AOC,OF⊥OE,若∠BOD=46°,则∠DOF的度数为 67 °.
【解答】解:∵OE平分∠AOC,
∴∠COE=∠AOC.
∵∠AOC=∠BOD,∠BOD=46°,
∴∠AOC=46°.
∴∠COE=×46°=23°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠DOF=180°﹣∠EOF﹣∠COE=180°﹣90°﹣23°=67°.
故答案为:67.
一十七.平行线的性质(共1小题)
47.(2021春 奉贤区期末)如图,将一块三角板的直角顶点放在直尺的一边上,若∠1=34°,则∠2= 56 °.
【解答】解:∵∠1=34°,
∴∠3=90°﹣34°=56°.
∵直尺的两边互相平行,
∴∠2=∠3=56°.
故答案为:56.
一十八.平行线的判定与性质(共1小题)
48.(2021春 黄浦区期末)如图,在四边形ABCD中,∠C+∠D=180°,∠A比∠B大40°,则∠B= 70° .
【解答】解:∵∠C+∠D=180°,
∴AD∥BC,
∴∠A+∠B=180°,
又∵∠A﹣∠B=40°,
∴∠A=110°,∠B=70°.
故答案为:70°.
一十九.平行线之间的距离(共1小题)
49.(2021春 静安区校级期末)如图,已知AB∥CD,AE∥FC,∠BAD=∠B=90°,图中表示AB与CD之间的距离是线段 BC或AD 的长度.
【解答】解∵∠BAD=∠B=90°,
∴∠BAD+∠B=180°,
∴AD∥BC(同旁内角互补,两直线平行),
又∵AB∥CD,∠BAD=90°,
∴四边形ABCD为矩形,
∴∠ABC=∠ACB=∠D=∠BAD=90°,
∴表示AB与CD之间的距离是线段BC或AD的长度.
二十.三角形的面积(共5小题)
50.(2021春 静安区校级期末)如图,已知直线a∥b,点B是线段AE的中点,S△ABD=2,则S△ACE= 4 .
【解答】解:假设两平行线间的距离为d,
则,,
又∵B是线段AE的中点,
∴AE=2AB,
∴==2S△ABD,
∵S△ABD=2,
∴S△ACE=4.
故答案为:4.
51.(2021春 嘉定区期末)如图,AD∥CE,△ACD的面积为a,那么△EAD的面积为 a .
【解答】解:∵AD∥CE,
∴C点和E点到AD的距离相等,
∴S△EAD=S△CAD=a.
故答案为:a.
52.(2021春 金山区期末)如图,已知在平面直角坐标系中,点A(2,﹣2)、点B(﹣3,4)、点C(﹣5,0),那么△ABC的面积等于 16 .
【解答】解:S△ABC=7×6﹣×2×4﹣×7×2﹣×6×5=16,
故答案为:16.
53.(2021春 松江区期末)如图,已知AB∥CD,CD=2AB,△ACD的面积为6,那么△ABC的面积为 3 .
【解答】解:∵AB∥CD,
∴△ACD和△ABC的高相等,
∵CD=2AB,
∴,
故答案为3.
54.(2021春 奉贤区期末)如图,AD∥BC,E是线段AD上任意一点,BE与AC相交于点O,若△ABC的面积是5,△EOC的面积是2,则△BOC的面积是 3 .
【解答】解:∵AD∥BC,
∴S△ABC=S△EBC=5,
又∵S△EOC=2,
∴S△BOC=S△EBC﹣S△EOC=5﹣2=3,
故答案为:3.
二十一.三角形内角和定理(共2小题)
55.(2021春 静安区校级期末)如图,直线l1∥l2∥l3,△ABC的顶点B、C分别在直线l2,l3上,如果∠ABC=60°,∠1=25°,那么∠2= 35 °.
【解答】解:如图:
∵l1∥l2∥l3,∴∠2=∠3,∠1=∠4,
∴∠ABC=∠2+∠1,∵∠ABC=60°,∠1=25°,
∴∠2=60°﹣25°=35°,
故答案为35.
56.(2021春 静安区期末)如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 46 度.
【解答】解:∵a∥b,
∴∠1=∠2+∠3,
∵∠1=126°,∠2=80°,
∴∠3=∠1﹣∠2=46°,
故答案为:46.
二十二.三角形的外角性质(共1小题)
57.(2021 昌平区二模)将一副三角板如图摆放,斜边AB与直角边DE相交于点F,则∠BFE= 60° .
【解答】解:∵∠DAE=∠E=45°,∠CAF=30°,
∴∠EAF=∠DAE﹣∠DAF=15°,
∴∠BFE=∠FAE+∠E=15°+45°=60°,
故答案为:60°.
二十三.全等三角形的判定与性质(共1小题)
58.(2021春 杨浦区期末)在△ABC与△DEF中,∠A=∠D,∠B=∠E,BC=EF,AB=3cm,AC=5cm,那么DE= 3 cm.
【解答】解:如图:
在△ABC与△DEF中,
,
∴△ABC≌△DEF中(AAS),
∴AB=DE,
∵AB=3cm,
∴DE=3cm,
故答案为:3.
二十四.关于x轴、y轴对称的点的坐标(共2小题)
59.(2021春 嘉定区期末)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 (3,﹣2) .
【解答】解:点(3,2)关于x轴对称的点的坐标为(3,﹣2).
故答案是:(3,﹣2).
60.(2021春 黄浦区期末)点A(1﹣a,5)和点B(3,b)关于y轴对称,则a+b= 9 .
【解答】解:∵点A(1﹣a,5)与B(3,b)关于y轴对称
∴a=4,b=5
∴a+b=4+5=9.
一十一.零指数幂(共1小题)
32.(2022 漳州模拟)计算:20= .
一十二.二次根式的乘除法(共1小题)
33.(2021春 浦东新区期末)计算:×= .
一十三.点的坐标(共10小题)
34.(2021春 静安区校级期末)点A(﹣1,2)在第 象限.
35.(2021春 静安区校级期末)如果点A(2,t)在x轴上,那么点B(t﹣2,t+1)在第 象限.
36.(2021春 闵行区期末)在平面直角坐标系xOy中,已知点A(2,n)在第四象限,点B(m,1)在第二象限,那么点C(m,n)在第 象限.
37.(2021春 奉贤区期末)在平面直角坐标系中,经过点M(2,5)且垂直y轴的直线可以表示为直线 .
38.(2021春 奉贤区期末)在平面直角坐标系中,点P(6﹣a,4)到两坐标轴的距离相等,那么a的值是 .
39.(2021春 静安区期末)在平面直角坐标系中,经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线 .
40.(2021春 静安区期末)在平面直角坐标系中,如果点Q(a+1,2﹣a)在x轴上,那么a= .
41.(2021春 杨浦区期末)如果点P(x,y)在第四象限,那么点Q(2﹣y,x+1)在第 象限.
42.(2021春 杨浦区期末)在平面直角坐标系中,如果点M(a+1,2﹣a)在y轴上,那么点M的坐标是 .
43.(2021春 浦东新区期末)如果点M(a,b)在第二象限,那么点N(﹣a,b+1)在第 象限.
一十四.方向角(共1小题)
44.(2021春 闵行区期末)点A位于点B的北偏东方向15°,若将点B以点A为旋转中心旋转90°落在点C处,则点A在点C的 方向.
一十五.对顶角、邻补角(共1小题)
45.(2021春 静安区期末)如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 度.
一十六.垂线(共1小题)
46.(2021春 松江区期末)如图,直线AB,CD相交于O,OE平分∠AOC,OF⊥OE,若∠BOD=46°,则∠DOF的度数为 °.
一十七.平行线的性质(共1小题)
47.(2021春 奉贤区期末)如图,将一块三角板的直角顶点放在直尺的一边上,若∠1=34°,则∠2= .
一十八.平行线的判定与性质(共1小题)
48.(2021春 黄浦区期末)如图,在四边形ABCD中,∠C+∠D=180°,∠A比∠B大40°,则∠B= .
一十九.平行线之间的距离(共1小题)
49.(2021春 静安区校级期末)如图,已知AB∥CD,AE∥FC,∠BAD=∠B=90°,图中表示AB与CD之间的距离是线段 的长度.
二十.三角形的面积(共5小题)
50.(2021春 静安区校级期末)如图,已知直线a∥b,点B是线段AE的中点,S△ABD=2,则S△ACE= .
51.(2021春 嘉定区期末)如图,AD∥CE,△ACD的面积为a,那么△EAD的面积为 .
52.(2021春 金山区期末)如图,已知在平面直角坐标系中,点A(2,﹣2)、点B(﹣3,4)、点C(﹣5,0),那么△ABC的面积等于 .
53.(2021春 松江区期末)如图,已知AB∥CD,CD=2AB,△ACD的面积为6,那么△ABC的面积为 .
54.(2021春 奉贤区期末)如图,AD∥BC,E是线段AD上任意一点,BE与AC相交于点O,若△ABC的面积是5,△EOC的面积是2,则△BOC的面积是 .
二十一.三角形内角和定理(共2小题)
55.(2021春 静安区校级期末)如图,直线l1∥l2∥l3,△ABC的顶点B、C分别在直线l2,l3上,如果∠ABC=60°,∠1=25°,那么∠2= °.
56.(2021春 静安区期末)如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 度.
二十二.三角形的外角性质(共1小题)
57.(2021 昌平区二模)将一副三角板如图摆放,斜边AB与直角边DE相交于点F,则∠BFE= .
二十三.全等三角形的判定与性质(共1小题)
58.(2021春 杨浦区期末)在△ABC与△DEF中,∠A=∠D,∠B=∠E,BC=EF,AB=3cm,AC=5cm,那么DE= cm.
二十四.关于x轴、y轴对称的点的坐标(共2小题)
59.(2021春 嘉定区期末)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 .
60.(2021春 黄浦区期末)点A(1﹣a,5)和点B(3,b)关于y轴对称,则a+b= .
参考答案与试题解析
一十一.零指数幂(共1小题)
32.(2022 漳州模拟)计算:20= 1 .
【解答】解:∵2≠0,
∴20=1.
故答案为:1.
一十二.二次根式的乘除法(共1小题)
33.(2021春 浦东新区期末)计算:×= 1 .
【解答】解:原式==1
故答案为:1
一十三.点的坐标(共10小题)
34.(2021春 静安区校级期末)点A(﹣1,2)在第 二 象限.
【解答】解:∵点A(﹣1,2)的横坐标小于零,纵坐标大于零,
∴点A(﹣1,2)在第二象限.
故答案为:二.
35.(2021春 静安区校级期末)如果点A(2,t)在x轴上,那么点B(t﹣2,t+1)在第 二 象限.
【解答】解:因为点A(2,t)在x轴上,
所以t=0,
则点B为(﹣2,1),
所以点B在第二象限.
故答案为:二.
36.(2021春 闵行区期末)在平面直角坐标系xOy中,已知点A(2,n)在第四象限,点B(m,1)在第二象限,那么点C(m,n)在第 三 象限.
【解答】解:∵点A(2,n)在第四象限,
∴n<0;
∵点B(m,1)在第二象限,
∴m<0,
∴点C(m,n)在第三象限.
故答案为:三.
37.(2021春 奉贤区期末)在平面直角坐标系中,经过点M(2,5)且垂直y轴的直线可以表示为直线 y=5 .
【解答】解:∵经过点M(2,5)且垂直于y轴,
∴直线可以表示为y=5.
故答案为:y=5.
38.(2021春 奉贤区期末)在平面直角坐标系中,点P(6﹣a,4)到两坐标轴的距离相等,那么a的值是 2或10 .
【解答】解:∵点P(6﹣a,4)到两坐标轴的距离相等,
∴|6﹣a|=4,
即6﹣a=4或6﹣a=﹣4,
解得a=2或a=10.
故答案为:2或10.
39.(2021春 静安区期末)在平面直角坐标系中,经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线 y=4 .
【解答】解:由题意得:经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线为:y=4,
故答案为:y=4.
40.(2021春 静安区期末)在平面直角坐标系中,如果点Q(a+1,2﹣a)在x轴上,那么a= 2 .
【解答】解:∵点Q(a+1,2﹣a)在x轴上,
∴2﹣a=0,
解得:a=2.
故答案为:2.
41.(2021春 杨浦区期末)如果点P(x,y)在第四象限,那么点Q(2﹣y,x+1)在第 一 象限.
【解答】解:∵点P(x,y)在第四象限,
∴x>0,y<0,
∴2﹣y>0,x+1>0,
∴Q(2﹣y,x+1)在第一象限.
故答案为:一.
42.(2021春 杨浦区期末)在平面直角坐标系中,如果点M(a+1,2﹣a)在y轴上,那么点M的坐标是 (0,3) .
【解答】解:∵M(a+1,2﹣a)在y轴上,
∴a+1=0,
解得a=﹣1,
∴2﹣a=2+1=3,
∴点M的坐标为(0,3).
故答案为:(0,3).
43.(2021春 浦东新区期末)如果点M(a,b)在第二象限,那么点N(﹣a,b+1)在第 一 象限.
【解答】解:∵点M(a,b)在第二象限,
∴a<0,b>0;
∴﹣a>0,b+1>1,
∴点N(﹣a,b+1)在第一象限.
故答案为:一.
一十四.方向角(共1小题)
44.(2021春 闵行区期末)点A位于点B的北偏东方向15°,若将点B以点A为旋转中心旋转90°落在点C处,则点A在点C的 北偏西75或南偏东75° 方向.
【解答】解:①若将点B以点A为旋转中心顺时针旋转90°落在点C处,则点A在点C的南偏东90°﹣15°=75°方向上,
②若将点B以点A为旋转中心逆时针旋转90°落在点C处,则点A在点C的北偏西90°﹣15°=75°方向上,
综上所述,点A在点C的北偏西75或南偏东75°方向,
故答案为:北偏西75或南偏东75°.
一十五.对顶角、邻补角(共1小题)
45.(2021春 静安区期末)如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 25 度.
【解答】解:∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD,
又∵∠ACO=∠BOD,
∴∠BOE=∠AOC=×50°=25°,
故答案为:25.
一十六.垂线(共1小题)
46.(2021春 松江区期末)如图,直线AB,CD相交于O,OE平分∠AOC,OF⊥OE,若∠BOD=46°,则∠DOF的度数为 67 °.
【解答】解:∵OE平分∠AOC,
∴∠COE=∠AOC.
∵∠AOC=∠BOD,∠BOD=46°,
∴∠AOC=46°.
∴∠COE=×46°=23°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠DOF=180°﹣∠EOF﹣∠COE=180°﹣90°﹣23°=67°.
故答案为:67.
一十七.平行线的性质(共1小题)
47.(2021春 奉贤区期末)如图,将一块三角板的直角顶点放在直尺的一边上,若∠1=34°,则∠2= 56 °.
【解答】解:∵∠1=34°,
∴∠3=90°﹣34°=56°.
∵直尺的两边互相平行,
∴∠2=∠3=56°.
故答案为:56.
一十八.平行线的判定与性质(共1小题)
48.(2021春 黄浦区期末)如图,在四边形ABCD中,∠C+∠D=180°,∠A比∠B大40°,则∠B= 70° .
【解答】解:∵∠C+∠D=180°,
∴AD∥BC,
∴∠A+∠B=180°,
又∵∠A﹣∠B=40°,
∴∠A=110°,∠B=70°.
故答案为:70°.
一十九.平行线之间的距离(共1小题)
49.(2021春 静安区校级期末)如图,已知AB∥CD,AE∥FC,∠BAD=∠B=90°,图中表示AB与CD之间的距离是线段 BC或AD 的长度.
【解答】解∵∠BAD=∠B=90°,
∴∠BAD+∠B=180°,
∴AD∥BC(同旁内角互补,两直线平行),
又∵AB∥CD,∠BAD=90°,
∴四边形ABCD为矩形,
∴∠ABC=∠ACB=∠D=∠BAD=90°,
∴表示AB与CD之间的距离是线段BC或AD的长度.
二十.三角形的面积(共5小题)
50.(2021春 静安区校级期末)如图,已知直线a∥b,点B是线段AE的中点,S△ABD=2,则S△ACE= 4 .
【解答】解:假设两平行线间的距离为d,
则,,
又∵B是线段AE的中点,
∴AE=2AB,
∴==2S△ABD,
∵S△ABD=2,
∴S△ACE=4.
故答案为:4.
51.(2021春 嘉定区期末)如图,AD∥CE,△ACD的面积为a,那么△EAD的面积为 a .
【解答】解:∵AD∥CE,
∴C点和E点到AD的距离相等,
∴S△EAD=S△CAD=a.
故答案为:a.
52.(2021春 金山区期末)如图,已知在平面直角坐标系中,点A(2,﹣2)、点B(﹣3,4)、点C(﹣5,0),那么△ABC的面积等于 16 .
【解答】解:S△ABC=7×6﹣×2×4﹣×7×2﹣×6×5=16,
故答案为:16.
53.(2021春 松江区期末)如图,已知AB∥CD,CD=2AB,△ACD的面积为6,那么△ABC的面积为 3 .
【解答】解:∵AB∥CD,
∴△ACD和△ABC的高相等,
∵CD=2AB,
∴,
故答案为3.
54.(2021春 奉贤区期末)如图,AD∥BC,E是线段AD上任意一点,BE与AC相交于点O,若△ABC的面积是5,△EOC的面积是2,则△BOC的面积是 3 .
【解答】解:∵AD∥BC,
∴S△ABC=S△EBC=5,
又∵S△EOC=2,
∴S△BOC=S△EBC﹣S△EOC=5﹣2=3,
故答案为:3.
二十一.三角形内角和定理(共2小题)
55.(2021春 静安区校级期末)如图,直线l1∥l2∥l3,△ABC的顶点B、C分别在直线l2,l3上,如果∠ABC=60°,∠1=25°,那么∠2= 35 °.
【解答】解:如图:
∵l1∥l2∥l3,∴∠2=∠3,∠1=∠4,
∴∠ABC=∠2+∠1,∵∠ABC=60°,∠1=25°,
∴∠2=60°﹣25°=35°,
故答案为35.
56.(2021春 静安区期末)如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 46 度.
【解答】解:∵a∥b,
∴∠1=∠2+∠3,
∵∠1=126°,∠2=80°,
∴∠3=∠1﹣∠2=46°,
故答案为:46.
二十二.三角形的外角性质(共1小题)
57.(2021 昌平区二模)将一副三角板如图摆放,斜边AB与直角边DE相交于点F,则∠BFE= 60° .
【解答】解:∵∠DAE=∠E=45°,∠CAF=30°,
∴∠EAF=∠DAE﹣∠DAF=15°,
∴∠BFE=∠FAE+∠E=15°+45°=60°,
故答案为:60°.
二十三.全等三角形的判定与性质(共1小题)
58.(2021春 杨浦区期末)在△ABC与△DEF中,∠A=∠D,∠B=∠E,BC=EF,AB=3cm,AC=5cm,那么DE= 3 cm.
【解答】解:如图:
在△ABC与△DEF中,
,
∴△ABC≌△DEF中(AAS),
∴AB=DE,
∵AB=3cm,
∴DE=3cm,
故答案为:3.
二十四.关于x轴、y轴对称的点的坐标(共2小题)
59.(2021春 嘉定区期末)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 (3,﹣2) .
【解答】解:点(3,2)关于x轴对称的点的坐标为(3,﹣2).
故答案是:(3,﹣2).
60.(2021春 黄浦区期末)点A(1﹣a,5)和点B(3,b)关于y轴对称,则a+b= 9 .
【解答】解:∵点A(1﹣a,5)与B(3,b)关于y轴对称
∴a=4,b=5
∴a+b=4+5=9.
同课章节目录
