03选择题(中档题)(含解析)- 2021年春上海市各区七年级(下)期末数学知识点分类汇编
文档属性
| 名称 | 03选择题(中档题)(含解析)- 2021年春上海市各区七年级(下)期末数学知识点分类汇编 |

|
|
| 格式 | doc | ||
| 文件大小 | 191.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 00:00:00 | ||
图片预览




文档简介
03选择题(中档题)
一.无理数(共1小题)
1.(2021春 浦东新区期末)下列实数中,一定是无理数的是( )
A. B.0.1010010001
C. D.3.14
二.估算无理数的大小(共1小题)
2.(2021春 浦东新区期末)估计的值在( )
A.3和4之间 B.5和6之间 C.7和8之间 D.14和15之间
三.分数指数幂(共1小题)
3.(2021春 静安区校级期末)下列说法正确的是( )
A.2的平方根是
B.数轴上的点与有理数——对应
C.1的n次方根是1
D.正实数包括正有理数和正无理数
四.二次根式的乘除法(共1小题)
4.(2021春 奉贤区期末)下列计算正确的是( )
A.=±9 B.(﹣)2=5 C.=﹣7 D.=3
五.点的坐标(共1小题)
5.(2021春 静安区期末)在平面直角坐标系第四象限中到x轴和y轴的距离分别是2、5的点的坐标为( )
A.(5,﹣2) B.(2,﹣5) C.(﹣5,2) D.(﹣2,﹣5)
六.钟面角(共1小题)
6.(2021春 静安区期末)早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( )
A.8点23分 B.8点25分 C.8点27分 D.9点整
七.点到直线的距离(共1小题)
7.(2021春 松江区期末)如图,点P是直线l外的一点,点A、B、C在直线l上,且PB⊥l,垂足是B,PA⊥PC,则下列判断不正确的是( )
A.线段PB的长是点P到直线l的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段PC的长是点C到直线PA的距离
八.同位角、内错角、同旁内角(共1小题)
8.(2021春 松江区期末)如图,下列判断正确的是( )
A.∠1与∠3是同位角 B.∠3与∠4是内错角
C.∠1与∠4是内错角 D.∠2与∠3是同位角
九.平行线的性质(共1小题)
9.(2021春 浦东新区期末)如图,由AB∥CD可以得到( )
A.∠BAC=∠DAC B.∠DAC=∠ACB
C.∠BAC=∠DCA D.∠D+∠DCB=180°
一十.三角形内角和定理(共3小题)
10.(2021春 奉贤区期末)已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
11.(2021春 浦东新区期末)若一个三角形的两个内角的度数分别为60°,50°,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
12.(2021春 杨浦区期末)下列说法中,正确的是( )
A.三角形的高都在三角形内
B.三角形的三条中线相交于三角形内一点
C.三角形的一个外角大于任何一个内角
D.三角形最大的一个内角的度数可以小于60度
一十一.全等三角形的判定(共4小题)
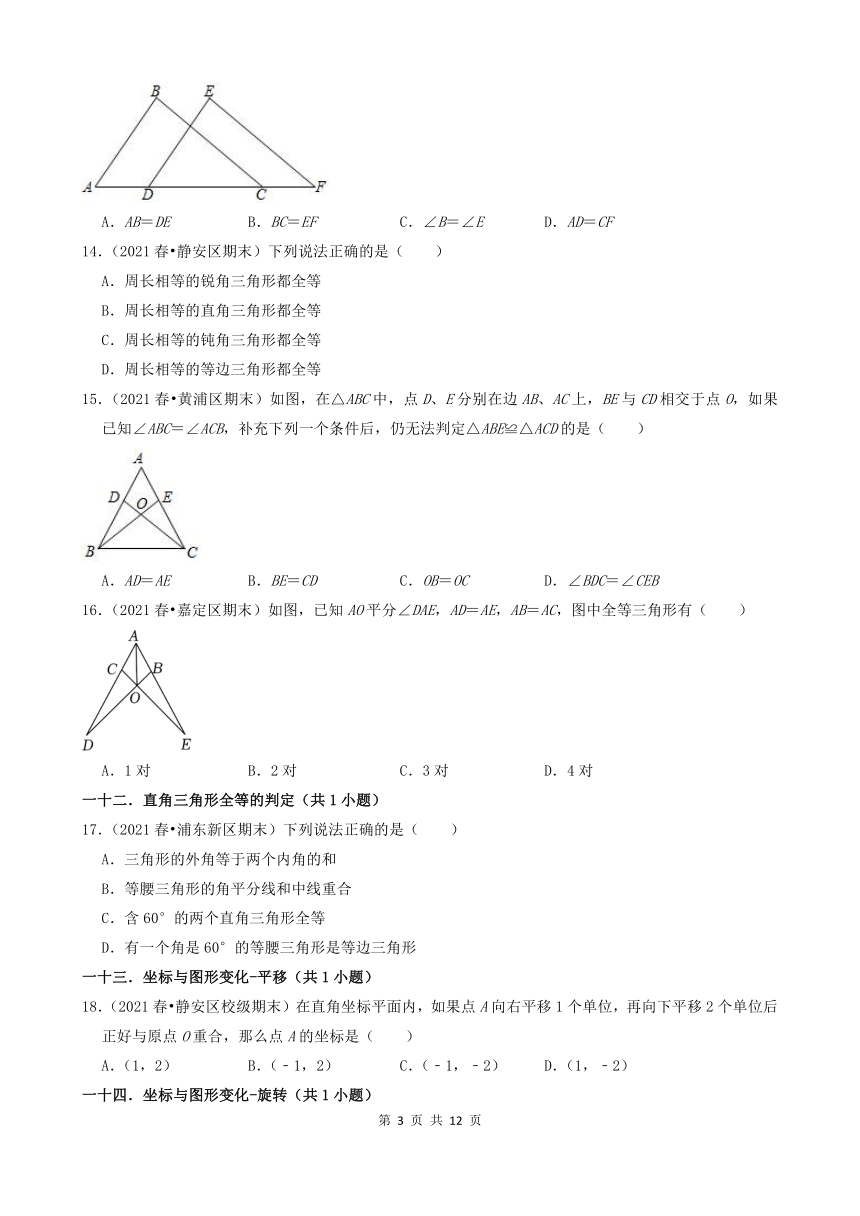
13.(2021春 松江区期末)如图,已知点A、D、C、F在同一条直线上,AB∥DE,BC∥EF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.BC=EF C.∠B=∠E D.AD=CF
14.(2021春 静安区期末)下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
15.(2021春 黄浦区期末)如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.OB=OC D.∠BDC=∠CEB
16.(2021春 嘉定区期末)如图,已知AO平分∠DAE,AD=AE,AB=AC,图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
一十二.直角三角形全等的判定(共1小题)
17.(2021春 浦东新区期末)下列说法正确的是( )
A.三角形的外角等于两个内角的和
B.等腰三角形的角平分线和中线重合
C.含60°的两个直角三角形全等
D.有一个角是60°的等腰三角形是等边三角形
一十三.坐标与图形变化-平移(共1小题)
18.(2021春 静安区校级期末)在直角坐标平面内,如果点A向右平移1个单位,再向下平移2个单位后正好与原点O重合,那么点A的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,﹣2) D.(1,﹣2)
一十四.坐标与图形变化-旋转(共1小题)
19.(2021 通州区模拟)在平面直角坐标系中,将点P(1,﹣2)绕原点旋转180°,得到的点Q的坐标为( )
A.(﹣1,2) B.(﹣1,﹣2) C.(1,2) D.(1,﹣2)
参考答案与试题解析
一.无理数(共1小题)
1.(2021春 浦东新区期末)下列实数中,一定是无理数的是( )
A. B.0.1010010001
C. D.3.14
【解答】解:A、是无理数,故此选项符合题意;
B、0.1010010001是有限小数,属于有理数,故此选项不符合题意;
C、是分数,属于有理数,故此选项不符合题意;
D、3.14是有限小数,属于有理数,故此选项不符合题意.
故选:A.
二.估算无理数的大小(共1小题)
2.(2021春 浦东新区期末)估计的值在( )
A.3和4之间 B.5和6之间 C.7和8之间 D.14和15之间
【解答】解:∵25<29<36,
∴,
∴5<<6,
故选:B.
三.分数指数幂(共1小题)
3.(2021春 静安区校级期末)下列说法正确的是( )
A.2的平方根是
B.数轴上的点与有理数——对应
C.1的n次方根是1
D.正实数包括正有理数和正无理数
【解答】解:A,2的平方根是,不符合题意.
B,数轴上的点与实数——对应,不符合题意.
C,1的偶数次方根是±1,不符合题意.
D,正实数包括正有理数和正无理数,符合题意.
故选:D.
四.二次根式的乘除法(共1小题)
4.(2021春 奉贤区期末)下列计算正确的是( )
A.=±9 B.(﹣)2=5 C.=﹣7 D.=3
【解答】解:∵=9,
∴A选项不符合题意;
∵=5,
∴B选项符合题意;
∵=7,
∴C选项不符合题意;
∵,
∴D选项不符合题意.
综上,B选项符合题意,
故选:B.
五.点的坐标(共1小题)
5.(2021春 静安区期末)在平面直角坐标系第四象限中到x轴和y轴的距离分别是2、5的点的坐标为( )
A.(5,﹣2) B.(2,﹣5) C.(﹣5,2) D.(﹣2,﹣5)
【解答】解:∵点B在第四象限,且到x轴的距离为2,到y轴的距离为5,
∴点B的横坐标为5,纵坐标为﹣2,
∴点B的坐标为(5,﹣2).
故选:A.
六.钟面角(共1小题)
6.(2021春 静安区期末)早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( )
A.8点23分 B.8点25分 C.8点27分 D.9点整
【解答】解:设t分后时钟的分针和时针第一次垂直,依题意有
6t﹣0.5t=360﹣120﹣90,
解得t=27.
故早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是8点27分.
故选:C.
七.点到直线的距离(共1小题)
7.(2021春 松江区期末)如图,点P是直线l外的一点,点A、B、C在直线l上,且PB⊥l,垂足是B,PA⊥PC,则下列判断不正确的是( )
A.线段PB的长是点P到直线l的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段PC的长是点C到直线PA的距离
【解答】解:A、线段PB的长度叫做点P到直线l的距离,原说法正确,故此选项不符合题意;
B、PA、PB、PC三条线段中,依据垂线段最短可知PB最短,原说法正确,故此选项不符合题意;
C、线段PA的长度叫做点A到直线PC的距离,原说法不正确,故此选项符合题意;
D、线段PC的长是点C到直线PA的距离,原说法正确,故此选项不符合题意;
故选:C.
八.同位角、内错角、同旁内角(共1小题)
8.(2021春 松江区期末)如图,下列判断正确的是( )
A.∠1与∠3是同位角 B.∠3与∠4是内错角
C.∠1与∠4是内错角 D.∠2与∠3是同位角
【解答】解:A、∠1与∠3是同位角,原题说法正确,故此选项符合题意;
B、∠3与∠4是同旁内角,原题说法错误确,故此选项不符合题意;
C、∠1与∠4不是内错角,原题说法错误,故此选项不符合题意;
D、∠2与∠3不是同旁内角,原题说法错误,故此选项不符合题意;
故选:A.
九.平行线的性质(共1小题)
9.(2021春 浦东新区期末)如图,由AB∥CD可以得到( )
A.∠BAC=∠DAC B.∠DAC=∠ACB
C.∠BAC=∠DCA D.∠D+∠DCB=180°
【解答】解:∵AB∥CD,
∴∠BAC=∠DCA,
故选:C.
一十.三角形内角和定理(共3小题)
10.(2021春 奉贤区期末)已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
【解答】解:选项A:∵∠A=40°,∠B=50°,
∴∠C=180°﹣∠A﹣∠B=90°.
∴△ABC是直角三角形.
选项B:∵∠A=90°,
∴△ABC是直角三角形.
选项C:∵∠A+B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°.
∴∠C=90°.
∴△ABC是直角三角形.
选项D:∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴3∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴无法确定△ABC是直角三角形.
故选:D.
11.(2021春 浦东新区期末)若一个三角形的两个内角的度数分别为60°,50°,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
【解答】解:∵三角形的两个内角度数分别为60°、50°,
∴这个三角形的第三个角为180°﹣60°﹣50°=70°,
∵最大的角70°是锐角,
∴这个三角形是锐角三角形.
故选:B.
12.(2021春 杨浦区期末)下列说法中,正确的是( )
A.三角形的高都在三角形内
B.三角形的三条中线相交于三角形内一点
C.三角形的一个外角大于任何一个内角
D.三角形最大的一个内角的度数可以小于60度
【解答】解:A、锐角三角形的三条高在三角形内部,相交于三角形内一点,故本选项错误;
B、三角形的三条中线相交于三角形内一点,故本选项正确;
C、三角形的一个外角大于任何一个不相邻的一个内角,故本选项错误;
D、根据三角形内角和等于180°,三角形最大的一个内角的度数大于或等于60度,故本选项错误;
故选:B.
一十一.全等三角形的判定(共4小题)
13.(2021春 松江区期末)如图,已知点A、D、C、F在同一条直线上,AB∥DE,BC∥EF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.BC=EF C.∠B=∠E D.AD=CF
【解答】解:A、添加AB=DE可用AAS进行判定,故本选项错误;
B、添加BC=EF可用AAS进行判定,故本选项错误;
C、添加∠B=∠E不能判定△ABC≌△DEF,故本选项正确;
D、添加AD=CF,得出AC=DF,然后可用ASA进行判定,故本选项错误;
故选:C.
14.(2021春 静安区期末)下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
【解答】解:周长相等的锐角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项A错误;
周长相等的直角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项B错误;
周长相等的钝角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项C错误;
周长相等的等边三角形一定全等,因为周长相等,三条边一定对应相等,利用SSS,可以说明两个三角形全等,故选项D正确;
故选:D.
15.(2021春 黄浦区期末)如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.OB=OC D.∠BDC=∠CEB
【解答】解:∵∠ABC=∠ACB,
∴AB=AC,
∵∠BAE=∠CAD,
∴补充条件AD=AE时,△ABE≌△ACD(SAS),故选项A不符合题意;
补充条件BE=CD,无法判断△ABE≌△ACD,故选项B符合题意;
补充条件OB=OC时,则∠OBC=∠OCB,故∠ABE=∠ACD,则△ABE≌△ACD(ASA),故选项C不符合题意;
补充条件∠BDC=∠CEB时,则∠AEB=∠ADC,则△ABE≌△ACD(AAS),故选项D不符合题意;
故选:B.
16.(2021春 嘉定区期末)如图,已知AO平分∠DAE,AD=AE,AB=AC,图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
【解答】解:∵AO平分∠DAE,
∴∠DAO=∠EAO,
在△DAO和△EAO中,
,
∴△DAO≌△EAO(SAS),
∴∠D=∠E,
∵AD=AE,AB=AC,
∴AD﹣AC=AE﹣AB,
即AC=AB,
在△ACO和△ABO中,
,
∴△ACO≌△ABO(SAS),
∴OC=OB,
在△DCO和△EBO中,
,
∴△DCO≌△EBO(AAS),
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
即全等三角形有4对,
故选:D.
一十二.直角三角形全等的判定(共1小题)
17.(2021春 浦东新区期末)下列说法正确的是( )
A.三角形的外角等于两个内角的和
B.等腰三角形的角平分线和中线重合
C.含60°的两个直角三角形全等
D.有一个角是60°的等腰三角形是等边三角形
【解答】解:A、三角形的外角等于与它不相邻的两个内角之和,本选项说法不正确;
B、等腰三角形的顶角平分线和中线重合,本选项说法不正确;
C、含有60°的两个直角三角形的对应边不一定相等,则这两个直角三角形不一定全等,本选项说法不正确;
D、有一个角是60°的等腰三角形是等边三角形,本选项说法正确;
故选:D.
一十三.坐标与图形变化-平移(共1小题)
18.(2021春 静安区校级期末)在直角坐标平面内,如果点A向右平移1个单位,再向下平移2个单位后正好与原点O重合,那么点A的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,﹣2) D.(1,﹣2)
【解答】解:∵将点A(a,b)向右平移1单位长度,再向下平移2个单位长度正好与原点重合,
∴a+1=0,b﹣2=0,
∴a=﹣1,b=2,
∴点A的坐标是(﹣1,2),
故选:B.
一十四.坐标与图形变化-旋转(共1小题)
19.(2021 通州区模拟)在平面直角坐标系中,将点P(1,﹣2)绕原点旋转180°,得到的点Q的坐标为( )
A.(﹣1,2) B.(﹣1,﹣2) C.(1,2) D.(1,﹣2)
【解答】解:∵将点P(1,﹣2)绕原点O旋转180°后,得到的对应点Q,
∴点Q和点P关于原点对称,
∵点P的坐标为(1,﹣2),
∴点Q的坐标是(﹣1,2).
故选:A.
一.无理数(共1小题)
1.(2021春 浦东新区期末)下列实数中,一定是无理数的是( )
A. B.0.1010010001
C. D.3.14
二.估算无理数的大小(共1小题)
2.(2021春 浦东新区期末)估计的值在( )
A.3和4之间 B.5和6之间 C.7和8之间 D.14和15之间
三.分数指数幂(共1小题)
3.(2021春 静安区校级期末)下列说法正确的是( )
A.2的平方根是
B.数轴上的点与有理数——对应
C.1的n次方根是1
D.正实数包括正有理数和正无理数
四.二次根式的乘除法(共1小题)
4.(2021春 奉贤区期末)下列计算正确的是( )
A.=±9 B.(﹣)2=5 C.=﹣7 D.=3
五.点的坐标(共1小题)
5.(2021春 静安区期末)在平面直角坐标系第四象限中到x轴和y轴的距离分别是2、5的点的坐标为( )
A.(5,﹣2) B.(2,﹣5) C.(﹣5,2) D.(﹣2,﹣5)
六.钟面角(共1小题)
6.(2021春 静安区期末)早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( )
A.8点23分 B.8点25分 C.8点27分 D.9点整
七.点到直线的距离(共1小题)
7.(2021春 松江区期末)如图,点P是直线l外的一点,点A、B、C在直线l上,且PB⊥l,垂足是B,PA⊥PC,则下列判断不正确的是( )
A.线段PB的长是点P到直线l的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段PC的长是点C到直线PA的距离
八.同位角、内错角、同旁内角(共1小题)
8.(2021春 松江区期末)如图,下列判断正确的是( )
A.∠1与∠3是同位角 B.∠3与∠4是内错角
C.∠1与∠4是内错角 D.∠2与∠3是同位角
九.平行线的性质(共1小题)
9.(2021春 浦东新区期末)如图,由AB∥CD可以得到( )
A.∠BAC=∠DAC B.∠DAC=∠ACB
C.∠BAC=∠DCA D.∠D+∠DCB=180°
一十.三角形内角和定理(共3小题)
10.(2021春 奉贤区期末)已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
11.(2021春 浦东新区期末)若一个三角形的两个内角的度数分别为60°,50°,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
12.(2021春 杨浦区期末)下列说法中,正确的是( )
A.三角形的高都在三角形内
B.三角形的三条中线相交于三角形内一点
C.三角形的一个外角大于任何一个内角
D.三角形最大的一个内角的度数可以小于60度
一十一.全等三角形的判定(共4小题)
13.(2021春 松江区期末)如图,已知点A、D、C、F在同一条直线上,AB∥DE,BC∥EF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.BC=EF C.∠B=∠E D.AD=CF
14.(2021春 静安区期末)下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
15.(2021春 黄浦区期末)如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.OB=OC D.∠BDC=∠CEB
16.(2021春 嘉定区期末)如图,已知AO平分∠DAE,AD=AE,AB=AC,图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
一十二.直角三角形全等的判定(共1小题)
17.(2021春 浦东新区期末)下列说法正确的是( )
A.三角形的外角等于两个内角的和
B.等腰三角形的角平分线和中线重合
C.含60°的两个直角三角形全等
D.有一个角是60°的等腰三角形是等边三角形
一十三.坐标与图形变化-平移(共1小题)
18.(2021春 静安区校级期末)在直角坐标平面内,如果点A向右平移1个单位,再向下平移2个单位后正好与原点O重合,那么点A的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,﹣2) D.(1,﹣2)
一十四.坐标与图形变化-旋转(共1小题)
19.(2021 通州区模拟)在平面直角坐标系中,将点P(1,﹣2)绕原点旋转180°,得到的点Q的坐标为( )
A.(﹣1,2) B.(﹣1,﹣2) C.(1,2) D.(1,﹣2)
参考答案与试题解析
一.无理数(共1小题)
1.(2021春 浦东新区期末)下列实数中,一定是无理数的是( )
A. B.0.1010010001
C. D.3.14
【解答】解:A、是无理数,故此选项符合题意;
B、0.1010010001是有限小数,属于有理数,故此选项不符合题意;
C、是分数,属于有理数,故此选项不符合题意;
D、3.14是有限小数,属于有理数,故此选项不符合题意.
故选:A.
二.估算无理数的大小(共1小题)
2.(2021春 浦东新区期末)估计的值在( )
A.3和4之间 B.5和6之间 C.7和8之间 D.14和15之间
【解答】解:∵25<29<36,
∴,
∴5<<6,
故选:B.
三.分数指数幂(共1小题)
3.(2021春 静安区校级期末)下列说法正确的是( )
A.2的平方根是
B.数轴上的点与有理数——对应
C.1的n次方根是1
D.正实数包括正有理数和正无理数
【解答】解:A,2的平方根是,不符合题意.
B,数轴上的点与实数——对应,不符合题意.
C,1的偶数次方根是±1,不符合题意.
D,正实数包括正有理数和正无理数,符合题意.
故选:D.
四.二次根式的乘除法(共1小题)
4.(2021春 奉贤区期末)下列计算正确的是( )
A.=±9 B.(﹣)2=5 C.=﹣7 D.=3
【解答】解:∵=9,
∴A选项不符合题意;
∵=5,
∴B选项符合题意;
∵=7,
∴C选项不符合题意;
∵,
∴D选项不符合题意.
综上,B选项符合题意,
故选:B.
五.点的坐标(共1小题)
5.(2021春 静安区期末)在平面直角坐标系第四象限中到x轴和y轴的距离分别是2、5的点的坐标为( )
A.(5,﹣2) B.(2,﹣5) C.(﹣5,2) D.(﹣2,﹣5)
【解答】解:∵点B在第四象限,且到x轴的距离为2,到y轴的距离为5,
∴点B的横坐标为5,纵坐标为﹣2,
∴点B的坐标为(5,﹣2).
故选:A.
六.钟面角(共1小题)
6.(2021春 静安区期末)早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( )
A.8点23分 B.8点25分 C.8点27分 D.9点整
【解答】解:设t分后时钟的分针和时针第一次垂直,依题意有
6t﹣0.5t=360﹣120﹣90,
解得t=27.
故早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是8点27分.
故选:C.
七.点到直线的距离(共1小题)
7.(2021春 松江区期末)如图,点P是直线l外的一点,点A、B、C在直线l上,且PB⊥l,垂足是B,PA⊥PC,则下列判断不正确的是( )
A.线段PB的长是点P到直线l的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段PC的长是点C到直线PA的距离
【解答】解:A、线段PB的长度叫做点P到直线l的距离,原说法正确,故此选项不符合题意;
B、PA、PB、PC三条线段中,依据垂线段最短可知PB最短,原说法正确,故此选项不符合题意;
C、线段PA的长度叫做点A到直线PC的距离,原说法不正确,故此选项符合题意;
D、线段PC的长是点C到直线PA的距离,原说法正确,故此选项不符合题意;
故选:C.
八.同位角、内错角、同旁内角(共1小题)
8.(2021春 松江区期末)如图,下列判断正确的是( )
A.∠1与∠3是同位角 B.∠3与∠4是内错角
C.∠1与∠4是内错角 D.∠2与∠3是同位角
【解答】解:A、∠1与∠3是同位角,原题说法正确,故此选项符合题意;
B、∠3与∠4是同旁内角,原题说法错误确,故此选项不符合题意;
C、∠1与∠4不是内错角,原题说法错误,故此选项不符合题意;
D、∠2与∠3不是同旁内角,原题说法错误,故此选项不符合题意;
故选:A.
九.平行线的性质(共1小题)
9.(2021春 浦东新区期末)如图,由AB∥CD可以得到( )
A.∠BAC=∠DAC B.∠DAC=∠ACB
C.∠BAC=∠DCA D.∠D+∠DCB=180°
【解答】解:∵AB∥CD,
∴∠BAC=∠DCA,
故选:C.
一十.三角形内角和定理(共3小题)
10.(2021春 奉贤区期末)已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
【解答】解:选项A:∵∠A=40°,∠B=50°,
∴∠C=180°﹣∠A﹣∠B=90°.
∴△ABC是直角三角形.
选项B:∵∠A=90°,
∴△ABC是直角三角形.
选项C:∵∠A+B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°.
∴∠C=90°.
∴△ABC是直角三角形.
选项D:∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴3∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴无法确定△ABC是直角三角形.
故选:D.
11.(2021春 浦东新区期末)若一个三角形的两个内角的度数分别为60°,50°,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
【解答】解:∵三角形的两个内角度数分别为60°、50°,
∴这个三角形的第三个角为180°﹣60°﹣50°=70°,
∵最大的角70°是锐角,
∴这个三角形是锐角三角形.
故选:B.
12.(2021春 杨浦区期末)下列说法中,正确的是( )
A.三角形的高都在三角形内
B.三角形的三条中线相交于三角形内一点
C.三角形的一个外角大于任何一个内角
D.三角形最大的一个内角的度数可以小于60度
【解答】解:A、锐角三角形的三条高在三角形内部,相交于三角形内一点,故本选项错误;
B、三角形的三条中线相交于三角形内一点,故本选项正确;
C、三角形的一个外角大于任何一个不相邻的一个内角,故本选项错误;
D、根据三角形内角和等于180°,三角形最大的一个内角的度数大于或等于60度,故本选项错误;
故选:B.
一十一.全等三角形的判定(共4小题)
13.(2021春 松江区期末)如图,已知点A、D、C、F在同一条直线上,AB∥DE,BC∥EF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.BC=EF C.∠B=∠E D.AD=CF
【解答】解:A、添加AB=DE可用AAS进行判定,故本选项错误;
B、添加BC=EF可用AAS进行判定,故本选项错误;
C、添加∠B=∠E不能判定△ABC≌△DEF,故本选项正确;
D、添加AD=CF,得出AC=DF,然后可用ASA进行判定,故本选项错误;
故选:C.
14.(2021春 静安区期末)下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
【解答】解:周长相等的锐角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项A错误;
周长相等的直角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项B错误;
周长相等的钝角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项C错误;
周长相等的等边三角形一定全等,因为周长相等,三条边一定对应相等,利用SSS,可以说明两个三角形全等,故选项D正确;
故选:D.
15.(2021春 黄浦区期末)如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.OB=OC D.∠BDC=∠CEB
【解答】解:∵∠ABC=∠ACB,
∴AB=AC,
∵∠BAE=∠CAD,
∴补充条件AD=AE时,△ABE≌△ACD(SAS),故选项A不符合题意;
补充条件BE=CD,无法判断△ABE≌△ACD,故选项B符合题意;
补充条件OB=OC时,则∠OBC=∠OCB,故∠ABE=∠ACD,则△ABE≌△ACD(ASA),故选项C不符合题意;
补充条件∠BDC=∠CEB时,则∠AEB=∠ADC,则△ABE≌△ACD(AAS),故选项D不符合题意;
故选:B.
16.(2021春 嘉定区期末)如图,已知AO平分∠DAE,AD=AE,AB=AC,图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
【解答】解:∵AO平分∠DAE,
∴∠DAO=∠EAO,
在△DAO和△EAO中,
,
∴△DAO≌△EAO(SAS),
∴∠D=∠E,
∵AD=AE,AB=AC,
∴AD﹣AC=AE﹣AB,
即AC=AB,
在△ACO和△ABO中,
,
∴△ACO≌△ABO(SAS),
∴OC=OB,
在△DCO和△EBO中,
,
∴△DCO≌△EBO(AAS),
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
即全等三角形有4对,
故选:D.
一十二.直角三角形全等的判定(共1小题)
17.(2021春 浦东新区期末)下列说法正确的是( )
A.三角形的外角等于两个内角的和
B.等腰三角形的角平分线和中线重合
C.含60°的两个直角三角形全等
D.有一个角是60°的等腰三角形是等边三角形
【解答】解:A、三角形的外角等于与它不相邻的两个内角之和,本选项说法不正确;
B、等腰三角形的顶角平分线和中线重合,本选项说法不正确;
C、含有60°的两个直角三角形的对应边不一定相等,则这两个直角三角形不一定全等,本选项说法不正确;
D、有一个角是60°的等腰三角形是等边三角形,本选项说法正确;
故选:D.
一十三.坐标与图形变化-平移(共1小题)
18.(2021春 静安区校级期末)在直角坐标平面内,如果点A向右平移1个单位,再向下平移2个单位后正好与原点O重合,那么点A的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,﹣2) D.(1,﹣2)
【解答】解:∵将点A(a,b)向右平移1单位长度,再向下平移2个单位长度正好与原点重合,
∴a+1=0,b﹣2=0,
∴a=﹣1,b=2,
∴点A的坐标是(﹣1,2),
故选:B.
一十四.坐标与图形变化-旋转(共1小题)
19.(2021 通州区模拟)在平面直角坐标系中,将点P(1,﹣2)绕原点旋转180°,得到的点Q的坐标为( )
A.(﹣1,2) B.(﹣1,﹣2) C.(1,2) D.(1,﹣2)
【解答】解:∵将点P(1,﹣2)绕原点O旋转180°后,得到的对应点Q,
∴点Q和点P关于原点对称,
∵点P的坐标为(1,﹣2),
∴点Q的坐标是(﹣1,2).
故选:A.
同课章节目录
