北京课改版数学七年级下册同步课时练习:7.7.2 对顶角(word版含答案)
文档属性
| 名称 | 北京课改版数学七年级下册同步课时练习:7.7.2 对顶角(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 149.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览


文档简介
7.7 2.对顶角
对顶角:如果两个角有共同的顶点,并且其中一个角的两边分别是另一个角的两边的反向延长线,那么称这两个角互为对顶角.
对顶角相等.
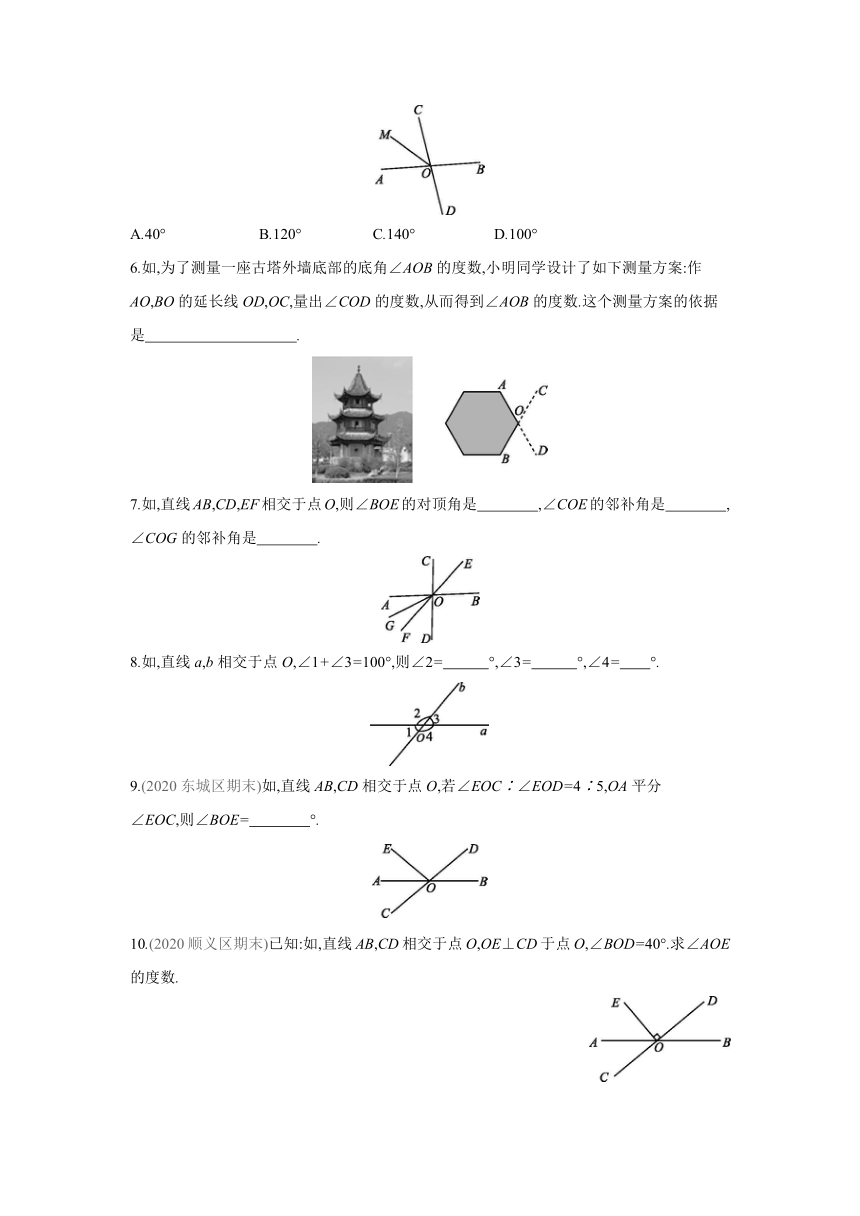
1.下列说法中正确的是 ( )
A.有公共顶点的角是对顶角 B.相等的角是对顶角
C.对顶角一定相等 D.不是对顶角的角不相等
2.下列形中,∠1与∠2是对顶角的是 ( )
3.如所示,直线AB与CD相交形成了∠1,∠2,∠3和∠4,若要确定这4个角的度数,至少要测量其中的 ( )
A.1个角 B.2个角
C.3个角 D.4个角
4.(2020密云区期末)如,直线AB与CD相交于点O,∠AOE与∠AOC互余,∠AOE=20°,则∠BOD的度数为 ( )
A.20° B.70°
C.90° D.110°
5.如,两条直线AB,CD相交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则
∠BOM等于 ( )
A.40° B.120° C.140° D.100°
6.如,为了测量一座古塔外墙底部的底角∠AOB的度数,小明同学设计了如下测量方案:作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是 .
7.如,直线AB,CD,EF相交于点O,则∠BOE的对顶角是 ,∠COE的邻补角是 ,∠COG的邻补角是 .
8.如,直线a,b相交于点O,∠1+∠3=100°,则∠2= °,∠3= °,∠4= °.
9.(2020东城区期末)如,直线AB,CD相交于点O,若∠EOC∶∠EOD=4∶5,OA平分
∠EOC,则∠BOE= °.
10.(2020顺义区期末)已知:如,直线AB,CD相交于点O,OE⊥CD于点O,∠BOD=40°.求∠AOE的度数.
11.如,直线a,b,c两两相交,∠1=60°,∠2=∠4,求∠2,∠3,∠5的度数.
12.如,直线AB与CD相交于点O,OE平分∠AOC,OF平分∠BOD,试说明点E,O,F在同一条直线上.
13.如,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
14.观察,寻找对顶角(不含平角):
(1)如①,中共有 对对顶角;
(2)如②,中共有 对对顶角;
(3)如③,中共有 对对顶角;
(4)研究①~③中直线的条数与对顶角的对数之间的关系,可得到:若有n条直线相交于一点,则可形成 对对顶角;
(5)若有10条直线相交于一点,则可形成多少对对顶角
答案
7.7 2.对顶角
1.C 2.D 3.A 4.B 5.C 6.对顶角相等
7.∠AOF ∠COF,∠EOD ∠GOD
8.130 50 130 解: 此题结合形,运用对顶角的性质与平角的定义进行计算,中等难度.
∵直线a,b相交于点O,
∴∠1=∠3.
∵∠1+∠3=100°,
∴2∠1=100°,
∴∠1=50°,
∴∠3=50°.
∵∠1+∠2=180°,
∴∠2=130°.
∵∠2=∠4,
∴∠4=130°.
9.140 解: ∵∠EOC∶∠EOD=4∶5,
∴设∠EOC=4x,∠EOD=5x,
故4x+5x=180°,
解得x=20°,
可得∠EOC=80°,∠EOD=100°.
∵OA平分∠EOC,
∴∠COA=∠AOE=40°,
∴∠BOE=180°-∠AOE=140°.
故答案为140.
10.解:法一:∵直线AB,CD相交于点O,
∠BOD=40°,
∴∠AOC=∠BOD=40°.
∵OE⊥CD于点O,
∴∠EOC=90°,
∴∠AOE=∠EOC-∠AOC=90°-40°=50°.
法二:∵OE⊥CD于点O,
∴∠EOD=90°.
∵∠AOE+∠EOD+∠BOD=180°,
∠BOD=40°,
∴∠AOE=50°.
11.解:因为∠1=∠2,∠1=60°,所以∠2=60°,所以∠3=180°-∠2=180°-60°=120°.因为∠2=∠4,所以∠4=90°,所以∠5=180°-∠4=180°-90°=90°.
12.解:如.∵OE平分∠AOC,OF平分∠BOD,
∴∠1=∠AOC,∠4=∠BOD.
∵直线AB与CD相交于点O,
∴∠AOC=∠BOD,∴∠1=∠4.
∵∠AOB=180°,∴∠2+∠3+∠4=180°.
∴∠3+∠2+∠1=180°,即∠EOF=180°.
∴点E,O,F在同一条直线上.
13.解:(1)因为∠AOC=46°,
所以∠AOD=180°-∠AOC=180°-46°=134°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=×134°=67°.
因为∠BOD=∠AOC=46°,
所以∠BOE=∠DOE+∠BOD=67°+46°=113°.
(2)因为∠AOC=x°,
所以∠AOD=180°-∠AOC=(180-x)°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=(180-x)°=90-x°.
因为∠BOD=∠AOC=x°,
所以∠BOE=∠DOE+∠BOD=90-x°+x°=90+x°.
14.(1)2 (2)6
(3)12 (4)n(n-1)
(5)90对
对顶角:如果两个角有共同的顶点,并且其中一个角的两边分别是另一个角的两边的反向延长线,那么称这两个角互为对顶角.
对顶角相等.
1.下列说法中正确的是 ( )
A.有公共顶点的角是对顶角 B.相等的角是对顶角
C.对顶角一定相等 D.不是对顶角的角不相等
2.下列形中,∠1与∠2是对顶角的是 ( )
3.如所示,直线AB与CD相交形成了∠1,∠2,∠3和∠4,若要确定这4个角的度数,至少要测量其中的 ( )
A.1个角 B.2个角
C.3个角 D.4个角
4.(2020密云区期末)如,直线AB与CD相交于点O,∠AOE与∠AOC互余,∠AOE=20°,则∠BOD的度数为 ( )
A.20° B.70°
C.90° D.110°
5.如,两条直线AB,CD相交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则
∠BOM等于 ( )
A.40° B.120° C.140° D.100°
6.如,为了测量一座古塔外墙底部的底角∠AOB的度数,小明同学设计了如下测量方案:作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是 .
7.如,直线AB,CD,EF相交于点O,则∠BOE的对顶角是 ,∠COE的邻补角是 ,∠COG的邻补角是 .
8.如,直线a,b相交于点O,∠1+∠3=100°,则∠2= °,∠3= °,∠4= °.
9.(2020东城区期末)如,直线AB,CD相交于点O,若∠EOC∶∠EOD=4∶5,OA平分
∠EOC,则∠BOE= °.
10.(2020顺义区期末)已知:如,直线AB,CD相交于点O,OE⊥CD于点O,∠BOD=40°.求∠AOE的度数.
11.如,直线a,b,c两两相交,∠1=60°,∠2=∠4,求∠2,∠3,∠5的度数.
12.如,直线AB与CD相交于点O,OE平分∠AOC,OF平分∠BOD,试说明点E,O,F在同一条直线上.
13.如,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
14.观察,寻找对顶角(不含平角):
(1)如①,中共有 对对顶角;
(2)如②,中共有 对对顶角;
(3)如③,中共有 对对顶角;
(4)研究①~③中直线的条数与对顶角的对数之间的关系,可得到:若有n条直线相交于一点,则可形成 对对顶角;
(5)若有10条直线相交于一点,则可形成多少对对顶角
答案
7.7 2.对顶角
1.C 2.D 3.A 4.B 5.C 6.对顶角相等
7.∠AOF ∠COF,∠EOD ∠GOD
8.130 50 130 解: 此题结合形,运用对顶角的性质与平角的定义进行计算,中等难度.
∵直线a,b相交于点O,
∴∠1=∠3.
∵∠1+∠3=100°,
∴2∠1=100°,
∴∠1=50°,
∴∠3=50°.
∵∠1+∠2=180°,
∴∠2=130°.
∵∠2=∠4,
∴∠4=130°.
9.140 解: ∵∠EOC∶∠EOD=4∶5,
∴设∠EOC=4x,∠EOD=5x,
故4x+5x=180°,
解得x=20°,
可得∠EOC=80°,∠EOD=100°.
∵OA平分∠EOC,
∴∠COA=∠AOE=40°,
∴∠BOE=180°-∠AOE=140°.
故答案为140.
10.解:法一:∵直线AB,CD相交于点O,
∠BOD=40°,
∴∠AOC=∠BOD=40°.
∵OE⊥CD于点O,
∴∠EOC=90°,
∴∠AOE=∠EOC-∠AOC=90°-40°=50°.
法二:∵OE⊥CD于点O,
∴∠EOD=90°.
∵∠AOE+∠EOD+∠BOD=180°,
∠BOD=40°,
∴∠AOE=50°.
11.解:因为∠1=∠2,∠1=60°,所以∠2=60°,所以∠3=180°-∠2=180°-60°=120°.因为∠2=∠4,所以∠4=90°,所以∠5=180°-∠4=180°-90°=90°.
12.解:如.∵OE平分∠AOC,OF平分∠BOD,
∴∠1=∠AOC,∠4=∠BOD.
∵直线AB与CD相交于点O,
∴∠AOC=∠BOD,∴∠1=∠4.
∵∠AOB=180°,∴∠2+∠3+∠4=180°.
∴∠3+∠2+∠1=180°,即∠EOF=180°.
∴点E,O,F在同一条直线上.
13.解:(1)因为∠AOC=46°,
所以∠AOD=180°-∠AOC=180°-46°=134°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=×134°=67°.
因为∠BOD=∠AOC=46°,
所以∠BOE=∠DOE+∠BOD=67°+46°=113°.
(2)因为∠AOC=x°,
所以∠AOD=180°-∠AOC=(180-x)°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=(180-x)°=90-x°.
因为∠BOD=∠AOC=x°,
所以∠BOE=∠DOE+∠BOD=90-x°+x°=90+x°.
14.(1)2 (2)6
(3)12 (4)n(n-1)
(5)90对
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
