北京课改版数学七年级下册同步课时练习:9.5.2 加权平均数(word版含答案)
文档属性
| 名称 | 北京课改版数学七年级下册同步课时练习:9.5.2 加权平均数(word版含答案) | 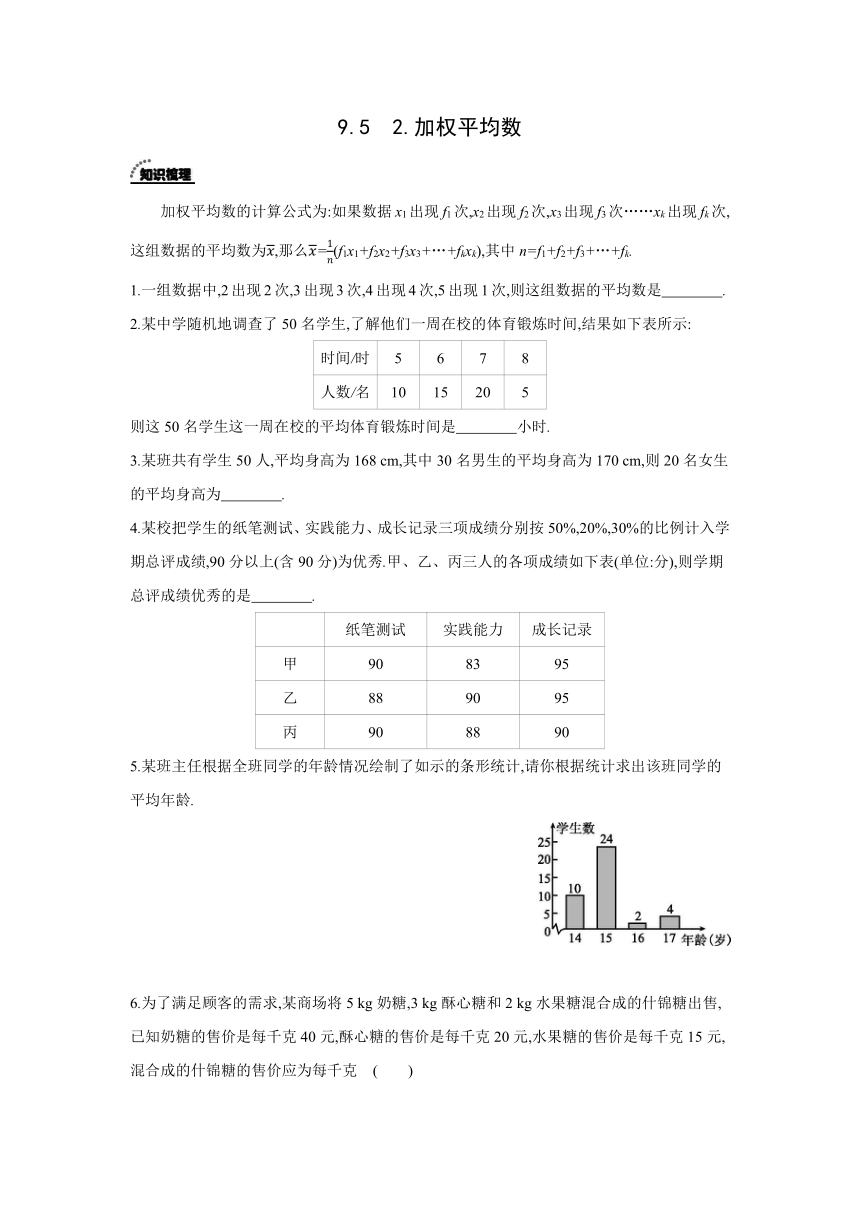 | |
| 格式 | docx | ||
| 文件大小 | 115.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 08:25:56 | ||
图片预览


文档简介
9.5 2.加权平均数
加权平均数的计算公式为:如果数据x1出现f1次,x2出现f2次,x3出现f3次……xk出现fk次,这组数据的平均数为,那么=(f1x1+f2x2+f3x3+…+fkxk),其中n=f1+f2+f3+…+fk.
1.一组数据中,2出现2次,3出现3次,4出现4次,5出现1次,则这组数据的平均数是 .
2.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
时间/时 5 6 7 8
人数/名 10 15 20 5
则这50名学生这一周在校的平均体育锻炼时间是 小时.
3.某班共有学生50人,平均身高为168 cm,其中30名男生的平均身高为170 cm,则20名女生的平均身高为 .
4.某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上(含90分)为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),则学期总评成绩优秀的是 .
纸笔测试 实践能力 成长记录
甲 90 83 95
乙 88 90 95
丙 90 88 90
5.某班主任根据全班同学的年龄情况绘制了如示的条形统计,请你根据统计求出该班同学的平均年龄.
6.为了满足顾客的需求,某商场将5 kg奶糖,3 kg酥心糖和2 kg水果糖混合成的什锦糖出售,已知奶糖的售价是每千克40元,酥心糖的售价是每千克20元,水果糖的售价是每千克15元,混合成的什锦糖的售价应为每千克 ( )
A.1.25元 B.28.5元
C.29元 D.34.5元
7.在某次射击训练中,某小组的成绩如下表所示:
成绩/环 7 8 9
人数 3 4
已知该小组的平均成绩为8环,那么成绩为9环的人数是 .
8.在一次英语口试中,得50分的有1人,得60分的有2人,得70分的有 5人,得90分的有5人,得100分的有1人,其余为82分.已知该班的平均成绩为80分,则该班有多少人
9.某班进行个人投篮比赛,下表(已被污损)记录了在规定时间内投进n个球的人数分布情况,同时,已知进球3个及3个以上的人平均每人投进3.5个球;进球4个及4个以下的人平均每人投进2.5个球,则投进3个球和4个球的人数分别为 .
进球数n 0 1 2 3 4 5
投进n个球的人数 1 2 7 2
10.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是 .
11.某校内商店销售单价分别为10元/个、15元/个、20元/个的三种文具,该商店统计了3月份的销售情况,并绘制成如示的统计.
(1)请将条形统计补充完整;
(2)计算总的平均销售单价是多少.
12.某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变,有关数据如下表所示.
景点 A B C D E
原价(元) 10 10 15 20 25
现价(元) 5 5 15 25 30
日平均人数(千人) 1 1 2 3 2
(1)该风景区称调价前后这5个景点门票的平均价格不变,日平均总收入持平,你知道该风景区是怎样计算的吗
(2)另一方面,游客认为调价后风景区的日平均总收入相对于调价前,实际上增加了约9.4%,你知道游客是怎样计算的吗
(3)你认为风景区和游客谁的说法能反映实际情况
答案
9.5 2.加权平均数
1.3.4
2.6.4 解: 根据题意,得(5×10+6×15+7×20+8×5)÷50=320÷50=6.4(时).
3.165 cm 4.甲和乙
5.解:(14×10+15×24+16×2+17×4)÷(10+24+2+4)=15(岁).
答:该班同学的平均年龄是15岁.
6.C 7.3
8.解:设该班有x人.由题意有50×1+60×2+70×5+90×5+100×1+82(x-1-2-5-5-1)=80x,
解得x=39.
答:该班有39人.
9.9,3 解: 设投进3个球的人数为a,投进4个球的人数为b.
根据题意,得=3.5,
=2.5,
即解得
10.
11.解:(1)由题意可得,销售单价为10元/个的文具的个数为90÷15%×25%=150,
补全条形统计如所示.
(2)总的平均销售单价是=14.5(元/个).
12.解:(1)风景区的算法是:调价前的平均价格为×(10+10+15+20+25)=16(元);
调价后的平均价格为×(5+5+15+25+30)=16(元).
因为调价前后的平均价格不变,日平均人数没有变化,因此风景区的日平均总收入没有变化.
(2)游客的计算方法:
调价前风景区的日平均总收入为10×1+10×1+15×2+20×3+25×2=160(千元);
调价后风景区的日平均总收入为5×1+5×1+15×2+25×3+30×2=175(千元),
所以风景区的日平均总收入增加了×100%≈9.4%.
(3)游客的说法能反映实际情况.
加权平均数的计算公式为:如果数据x1出现f1次,x2出现f2次,x3出现f3次……xk出现fk次,这组数据的平均数为,那么=(f1x1+f2x2+f3x3+…+fkxk),其中n=f1+f2+f3+…+fk.
1.一组数据中,2出现2次,3出现3次,4出现4次,5出现1次,则这组数据的平均数是 .
2.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
时间/时 5 6 7 8
人数/名 10 15 20 5
则这50名学生这一周在校的平均体育锻炼时间是 小时.
3.某班共有学生50人,平均身高为168 cm,其中30名男生的平均身高为170 cm,则20名女生的平均身高为 .
4.某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上(含90分)为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),则学期总评成绩优秀的是 .
纸笔测试 实践能力 成长记录
甲 90 83 95
乙 88 90 95
丙 90 88 90
5.某班主任根据全班同学的年龄情况绘制了如示的条形统计,请你根据统计求出该班同学的平均年龄.
6.为了满足顾客的需求,某商场将5 kg奶糖,3 kg酥心糖和2 kg水果糖混合成的什锦糖出售,已知奶糖的售价是每千克40元,酥心糖的售价是每千克20元,水果糖的售价是每千克15元,混合成的什锦糖的售价应为每千克 ( )
A.1.25元 B.28.5元
C.29元 D.34.5元
7.在某次射击训练中,某小组的成绩如下表所示:
成绩/环 7 8 9
人数 3 4
已知该小组的平均成绩为8环,那么成绩为9环的人数是 .
8.在一次英语口试中,得50分的有1人,得60分的有2人,得70分的有 5人,得90分的有5人,得100分的有1人,其余为82分.已知该班的平均成绩为80分,则该班有多少人
9.某班进行个人投篮比赛,下表(已被污损)记录了在规定时间内投进n个球的人数分布情况,同时,已知进球3个及3个以上的人平均每人投进3.5个球;进球4个及4个以下的人平均每人投进2.5个球,则投进3个球和4个球的人数分别为 .
进球数n 0 1 2 3 4 5
投进n个球的人数 1 2 7 2
10.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是 .
11.某校内商店销售单价分别为10元/个、15元/个、20元/个的三种文具,该商店统计了3月份的销售情况,并绘制成如示的统计.
(1)请将条形统计补充完整;
(2)计算总的平均销售单价是多少.
12.某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变,有关数据如下表所示.
景点 A B C D E
原价(元) 10 10 15 20 25
现价(元) 5 5 15 25 30
日平均人数(千人) 1 1 2 3 2
(1)该风景区称调价前后这5个景点门票的平均价格不变,日平均总收入持平,你知道该风景区是怎样计算的吗
(2)另一方面,游客认为调价后风景区的日平均总收入相对于调价前,实际上增加了约9.4%,你知道游客是怎样计算的吗
(3)你认为风景区和游客谁的说法能反映实际情况
答案
9.5 2.加权平均数
1.3.4
2.6.4 解: 根据题意,得(5×10+6×15+7×20+8×5)÷50=320÷50=6.4(时).
3.165 cm 4.甲和乙
5.解:(14×10+15×24+16×2+17×4)÷(10+24+2+4)=15(岁).
答:该班同学的平均年龄是15岁.
6.C 7.3
8.解:设该班有x人.由题意有50×1+60×2+70×5+90×5+100×1+82(x-1-2-5-5-1)=80x,
解得x=39.
答:该班有39人.
9.9,3 解: 设投进3个球的人数为a,投进4个球的人数为b.
根据题意,得=3.5,
=2.5,
即解得
10.
11.解:(1)由题意可得,销售单价为10元/个的文具的个数为90÷15%×25%=150,
补全条形统计如所示.
(2)总的平均销售单价是=14.5(元/个).
12.解:(1)风景区的算法是:调价前的平均价格为×(10+10+15+20+25)=16(元);
调价后的平均价格为×(5+5+15+25+30)=16(元).
因为调价前后的平均价格不变,日平均人数没有变化,因此风景区的日平均总收入没有变化.
(2)游客的计算方法:
调价前风景区的日平均总收入为10×1+10×1+15×2+20×3+25×2=160(千元);
调价后风景区的日平均总收入为5×1+5×1+15×2+25×3+30×2=175(千元),
所以风景区的日平均总收入增加了×100%≈9.4%.
(3)游客的说法能反映实际情况.
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
