北京课改版数学七年级下册同步课时练习:第四章 一元一次不等式和一元一次不等式组 单元测试(word版含答案)
文档属性
| 名称 | 北京课改版数学七年级下册同步课时练习:第四章 一元一次不等式和一元一次不等式组 单元测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 81.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 08:35:27 | ||
图片预览


文档简介
第四章 一元一次不等式和一元一次不等式组 单元测试
一、选择题(每小题4分,共28分)
1.有理数a,b,c在数轴上的对应点的位置如示,则下列结论正确的是 ( )
A.a>-2 B.|b|>1
C.a+c>0 D.abc>0
2.若x>y,则下列不等式中不一定成立的是 ( )
A.x+1>y+1 B.2x>2y
C.> D.x2>y2
3.不等式4(x-1)>3x-2的解集在数轴上的表示正确的是 ( )
4.对于不等式组(a,b是常数),下列说法正确的是 ( )
A.当aC.当a≥b时有解 D.当a=b时有解
5.已知关于x的不等式2x-a≤0的正整数解恰好是1,2,3,4,那么a的取值范围是 ( )
A.8≤a<10 B.8C.8≤a≤10 D.a>8
6.若关于x的不等式组的解集是x>1,则m的取值范围是 ( )
A.m≥1 B.m≤1
C.m≥0 D.m≤0
7.若关于x的不等式组的解集是-1A.1 B.-1
C.0 D.无法确定
二、填空题(每小题4分,共20分)
8.y的2倍与8的和不小于-3用不等式表示为 .
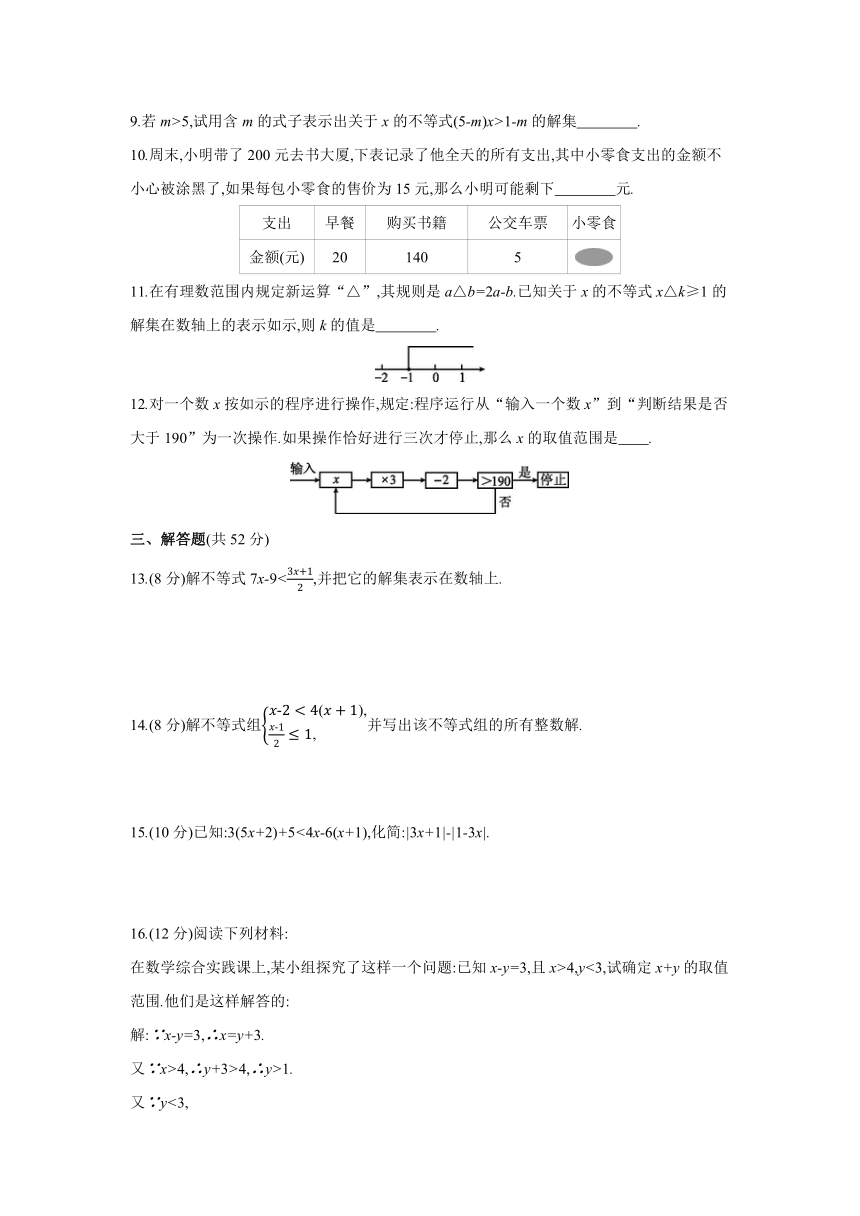
9.若m>5,试用含m的式子表示出关于x的不等式(5-m)x>1-m的解集 .
10.周末,小明带了200元去书大厦,下表记录了他全天的所有支出,其中小零食支出的金额不小心被涂黑了,如果每包小零食的售价为15元,那么小明可能剩下 元.
支出 早餐 购买书籍 公交车票 小零食
金额(元) 20 140 5
11.在有理数范围内规定新运算“△”,其规则是a△b=2a-b.已知关于x的不等式x△k≥1的解集在数轴上的表示如示,则k的值是 .
12.对一个数x按如示的程序进行操作,规定:程序运行从“输入一个数x”到“判断结果是否大于190”为一次操作.如果操作恰好进行三次才停止,那么x的取值范围是 .
三、解答题(共52分)
13.(8分)解不等式7x-9<,并把它的解集表示在数轴上.
14.(8分)解不等式组并写出该不等式组的所有整数解.
15.(10分)已知:3(5x+2)+5<4x-6(x+1),化简:|3x+1|-|1-3x|.
16.(12分)阅读下列材料:
在数学综合实践课上,某小组探究了这样一个问题:已知x-y=3,且x>4,y<3,试确定x+y的取值范围.他们是这样解答的:
解:∵x-y=3,∴x=y+3.
又∵x>4,∴y+3>4,∴y>1.
又∵y<3,
∴1同理可得4由①+②得4+1∴x+y的取值范围是5请仿照上述方法,解决下面的问题:
已知x+y=2,且x>1,y>-4,试确定x-y的取值范围.
17.(14分)某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机的进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.若商场用5万元共可购进A型号手机10部,B型号手机20部.
(1)求A,B两种型号的手机每部的进价各是多少元;
(2)为了满足市场需求,商场决定用不超过7.5万元采购A,B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍,则该商场有哪几种进货方案 并请你为商场选出获得利润最大的进货方案.
答案
自我综合评价(一)
1.C 2.D 3.A 4.B 5.A
6.D 解: 解不等式①,得x>1,解不等式② ,得x>m+1.因为不等式组的解集为x>1,所以m+1≤1,所以m≤0.
7.A 解: 原不等式组可化为
∵不等式组的解集是-1∴2+a=-1,=1,
∴a=-3,b=2,
∴(a+b)2022=(-1)2022=1.
故选A.
8.2y+8≥-3
9.x< 解: ∵m>5,∴5-m<0,
∴不等式(5-m)x>1-m的解集为x<.故答案为x<.
10.20或5 解: 设小明买了x包小零食.依题意,得
小明剩下的钱数可以表示为200-20-140-5-15x=(35-15x)元.
则35-15x≥0,∴x≤2.
∵x取正整数,
∴x的取值为1或2,
当x=1时,35-15x=35-15×1=20(元),
当x=2时,35-15x=35-15×2=5(元).
故答案为20或5.
11.-3
12.83x-2,3(3x-2)-2=9x-8,3(9x-8)-2=27x-26.
由已知得9x-8≤190,且27x-26>190.
解得8容易验证,当813.解:去分母,得2(7x-9)<3x+1.
去括号,得14x-18<3x+1.
移项、合并同类项,得11x<19.
系数化为1,得x<.
所以原不等式的解集是x<.
把它的解集表示在数轴上如所示.
14.解:
解不等式①,得x>-2,
解不等式②,得x≤3,
则不等式组的解集为-2所以不等式组的所有整数解为-1,0,1,2,3.
15.解:3(5x+2)+5<4x-6(x+1),
15x+6+5<4x-6x-6,
15x-4x+6x<-6-11,
17x<-17,
x<-1,
∴3x+1<0,1-3x>0,
∴|3x+1|-|1-3x|=-3x-1-1+3x=-2.
16.解:∵x+y=2,
∴x=2-y.
又∵x>1,
∴2-y>1,
∴-y>-1.
又∵y>-4,
∴-y<4,
∴-1<-y<4.……①
同理可得1由①+②得-1+1∴x-y的取值范围是017.解:(1)设B型号手机每部的进价为x元,则A型号手机每部的进价为(x+500)元.由题意,得10(x+500)+20x=50000,解得x=1500.则x+500=2000.
答:A型号手机每部的进价为2000元,B型号手机每部的进价为1500元.
(2)设商场购进A型号手机m部,则购进B型号手机(40-m)部.
由题意,得
解得≤m≤30.
∵m为整数,
∴m可取27,28,29,30,
∴共有四种进货方案:方案①,购进A型号手机27部,B型号手机13部;方案②,购进A型号手机28部,B型号手机12部;方案③,购进A型号手机29部,B型号手机11部;方案④,购进A型号手机30部,B型号手机10部.
设获得的利润为W元,则W=(2500-2000)m+(2100-1500)(40-m)=24000-100m.若W最大,则需m最小,∴当m=27,即选择购进A型号手机27部,B型号手机13部时获得的利润最大.
一、选择题(每小题4分,共28分)
1.有理数a,b,c在数轴上的对应点的位置如示,则下列结论正确的是 ( )
A.a>-2 B.|b|>1
C.a+c>0 D.abc>0
2.若x>y,则下列不等式中不一定成立的是 ( )
A.x+1>y+1 B.2x>2y
C.> D.x2>y2
3.不等式4(x-1)>3x-2的解集在数轴上的表示正确的是 ( )
4.对于不等式组(a,b是常数),下列说法正确的是 ( )
A.当a
5.已知关于x的不等式2x-a≤0的正整数解恰好是1,2,3,4,那么a的取值范围是 ( )
A.8≤a<10 B.8
6.若关于x的不等式组的解集是x>1,则m的取值范围是 ( )
A.m≥1 B.m≤1
C.m≥0 D.m≤0
7.若关于x的不等式组的解集是-1
C.0 D.无法确定
二、填空题(每小题4分,共20分)
8.y的2倍与8的和不小于-3用不等式表示为 .
9.若m>5,试用含m的式子表示出关于x的不等式(5-m)x>1-m的解集 .
10.周末,小明带了200元去书大厦,下表记录了他全天的所有支出,其中小零食支出的金额不小心被涂黑了,如果每包小零食的售价为15元,那么小明可能剩下 元.
支出 早餐 购买书籍 公交车票 小零食
金额(元) 20 140 5
11.在有理数范围内规定新运算“△”,其规则是a△b=2a-b.已知关于x的不等式x△k≥1的解集在数轴上的表示如示,则k的值是 .
12.对一个数x按如示的程序进行操作,规定:程序运行从“输入一个数x”到“判断结果是否大于190”为一次操作.如果操作恰好进行三次才停止,那么x的取值范围是 .
三、解答题(共52分)
13.(8分)解不等式7x-9<,并把它的解集表示在数轴上.
14.(8分)解不等式组并写出该不等式组的所有整数解.
15.(10分)已知:3(5x+2)+5<4x-6(x+1),化简:|3x+1|-|1-3x|.
16.(12分)阅读下列材料:
在数学综合实践课上,某小组探究了这样一个问题:已知x-y=3,且x>4,y<3,试确定x+y的取值范围.他们是这样解答的:
解:∵x-y=3,∴x=y+3.
又∵x>4,∴y+3>4,∴y>1.
又∵y<3,
∴1
已知x+y=2,且x>1,y>-4,试确定x-y的取值范围.
17.(14分)某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机的进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.若商场用5万元共可购进A型号手机10部,B型号手机20部.
(1)求A,B两种型号的手机每部的进价各是多少元;
(2)为了满足市场需求,商场决定用不超过7.5万元采购A,B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍,则该商场有哪几种进货方案 并请你为商场选出获得利润最大的进货方案.
答案
自我综合评价(一)
1.C 2.D 3.A 4.B 5.A
6.D 解: 解不等式①,得x>1,解不等式② ,得x>m+1.因为不等式组的解集为x>1,所以m+1≤1,所以m≤0.
7.A 解: 原不等式组可化为
∵不等式组的解集是-1
∴a=-3,b=2,
∴(a+b)2022=(-1)2022=1.
故选A.
8.2y+8≥-3
9.x< 解: ∵m>5,∴5-m<0,
∴不等式(5-m)x>1-m的解集为x<.故答案为x<.
10.20或5 解: 设小明买了x包小零食.依题意,得
小明剩下的钱数可以表示为200-20-140-5-15x=(35-15x)元.
则35-15x≥0,∴x≤2.
∵x取正整数,
∴x的取值为1或2,
当x=1时,35-15x=35-15×1=20(元),
当x=2时,35-15x=35-15×2=5(元).
故答案为20或5.
11.-3
12.8
由已知得9x-8≤190,且27x-26>190.
解得8
去括号,得14x-18<3x+1.
移项、合并同类项,得11x<19.
系数化为1,得x<.
所以原不等式的解集是x<.
把它的解集表示在数轴上如所示.
14.解:
解不等式①,得x>-2,
解不等式②,得x≤3,
则不等式组的解集为-2
15.解:3(5x+2)+5<4x-6(x+1),
15x+6+5<4x-6x-6,
15x-4x+6x<-6-11,
17x<-17,
x<-1,
∴3x+1<0,1-3x>0,
∴|3x+1|-|1-3x|=-3x-1-1+3x=-2.
16.解:∵x+y=2,
∴x=2-y.
又∵x>1,
∴2-y>1,
∴-y>-1.
又∵y>-4,
∴-y<4,
∴-1<-y<4.……①
同理可得1
答:A型号手机每部的进价为2000元,B型号手机每部的进价为1500元.
(2)设商场购进A型号手机m部,则购进B型号手机(40-m)部.
由题意,得
解得≤m≤30.
∵m为整数,
∴m可取27,28,29,30,
∴共有四种进货方案:方案①,购进A型号手机27部,B型号手机13部;方案②,购进A型号手机28部,B型号手机12部;方案③,购进A型号手机29部,B型号手机11部;方案④,购进A型号手机30部,B型号手机10部.
设获得的利润为W元,则W=(2500-2000)m+(2100-1500)(40-m)=24000-100m.若W最大,则需m最小,∴当m=27,即选择购进A型号手机27部,B型号手机13部时获得的利润最大.
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
