3 匀变速直线运动的位移与时间的关系
文档属性
| 名称 | 3 匀变速直线运动的位移与时间的关系 |  | |
| 格式 | zip | ||
| 文件大小 | 363.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2013-05-23 13:56:46 | ||
图片预览




文档简介
第八讲 3 匀变速直线运动的位移与时间的关系
情景导入
鸟击落飞机
中央电视台新闻联播中播出题目为:“但愿比翼飞,互相不干扰”的新闻报道.报道称:人类是从鸟的飞行中受到启发而制造出飞机的,但现在由于飞机在起飞和降落过程中,经常和栖息在机场附近的飞鸟相撞而导致“机毁鸟亡”,美国就发生此类事故300多起,致使各机场不得不耗费大量的人力、物力来驱赶机场附近的飞鸟.
假设某战斗机的起飞速度为50 m/s,在起飞时与一长度为10 cm的鸟相撞,把鸟撞成薄饼状贴在飞机上,则在撞机过程中,飞鸟的加速度约为多大
简答:战斗机的起飞速度为50 m/s,飞鸟忽略不计,由匀变速直线运动的位移与速度的关系式v2-v02=2ax,得飞鸟的加速度约为12 500 m/s2.
新知预习
匀速直线运动中的位移:对应着v-t图象中 .?
匀变速直线运动的位移:对应着v-t图象中 围成的面积.从此推导出的位移公式为: .?
匀变速直线运动的位移与速度的关系:v2-v02=2ax.
知识·巧学·升华
一、匀速直线运动的位移
1.匀速直线运动是物体沿一条直线运动,且速度保持不变的运动。它的特点是v大小方向都不变,位移x跟发生这段位移所用的时间t成正比。
2.位移公式:x=v-t。
3.匀速直线运动的v-t图象
(1)特点:图线与时间轴平行。
(2)由v-t图象可以获得的信息:
①任一时刻的速度大小和方向:若速度为正值,则图线位于时间轴上方;若速度为负值,则图线位于时间轴下方;若物体静止,则图线与时间轴重合。
②任一段时间内的位移:等于时间轴、速度图线、这段时间的初末时刻所包围的一块矩形的面积。若速度为正,则所包围的矩形位于时间轴的上方(如图2-3-1),说明这段位移的方向为正;若速度为负,则所包围的矩形位于时间轴的下方(图2-3-2),说明这段位移的方向为负。
向正方向的匀速直线运动 向负方向的匀速直线运动
图2-3-1 图2-3-2
4.匀速直线运动的x-t图象
图2-3-3
(1)特点:是一条倾斜直线。如图2-3-3。
(2)图象的含义
①表明在匀速直线运动中,x∝t。
②图象上任一点的横坐标表示运动的时间,对应的纵坐标表示位移。
③图象的斜率k=Δx/Δt=v。
二、匀变速直线运动的位移
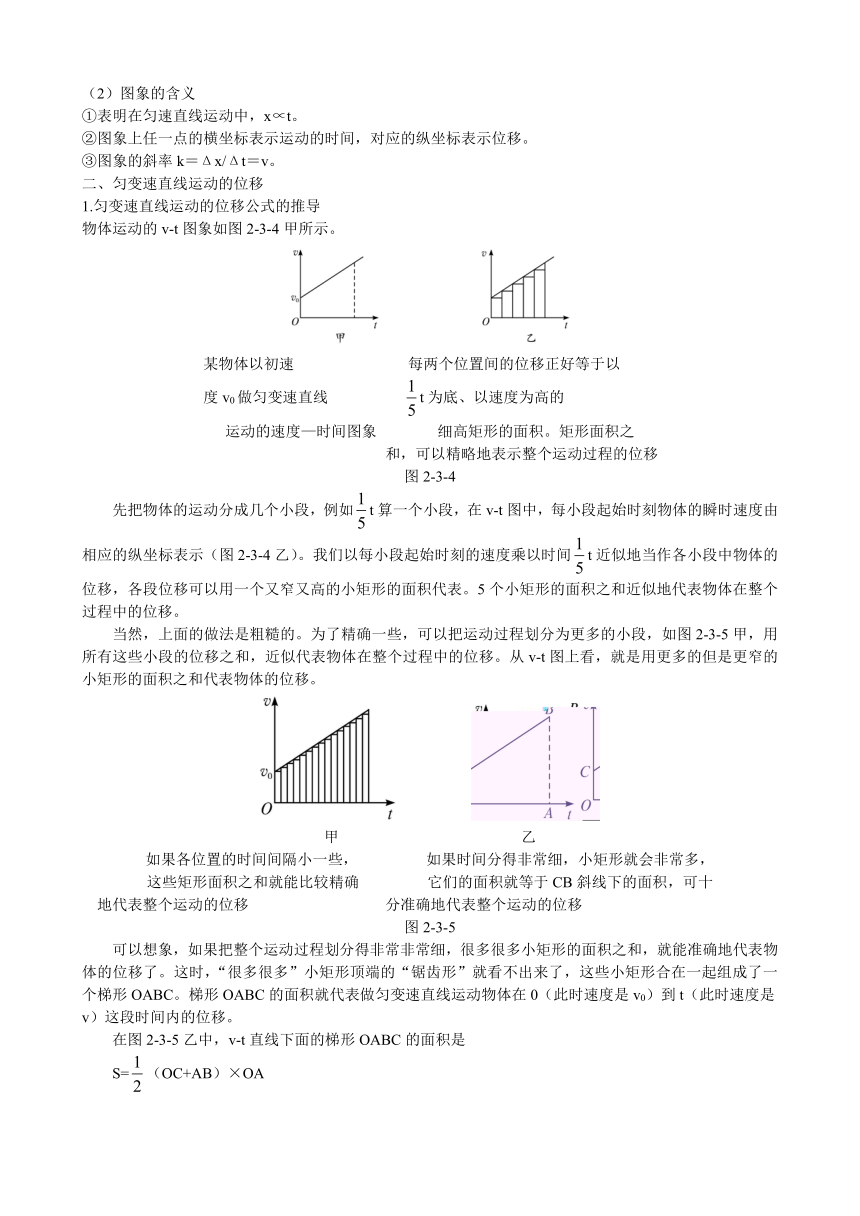
1.匀变速直线运动的位移公式的推导
物体运动的v-t图象如图2-3-4甲所示。
某物体以初速 每两个位置间的位移正好等于以
度v0做匀变速直线 t为底、以速度为高的
运动的速度—时间图象 细高矩形的面积。矩形面积之
和,可以精略地表示整个运动过程的位移
图2-3-4
先把物体的运动分成几个小段,例如t算一个小段,在v-t图中,每小段起始时刻物体的瞬时速度由相应的纵坐标表示(图2-3-4乙)。我们以每小段起始时刻的速度乘以时间t近似地当作各小段中物体的位移,各段位移可以用一个又窄又高的小矩形的面积代表。5个小矩形的面积之和近似地代表物体在整个过程中的位移。
当然,上面的做法是粗糙的。为了精确一些,可以把运动过程划分为更多的小段,如图2-3-5甲,用所有这些小段的位移之和,近似代表物体在整个过程中的位移。从v-t图上看,就是用更多的但是更窄的小矩形的面积之和代表物体的位移。
甲 乙
如果各位置的时间间隔小一些, 如果时间分得非常细,小矩形就会非常多,
这些矩形面积之和就能比较精确 它们的面积就等于CB斜线下的面积,可十
地代表整个运动的位移 分准确地代表整个运动的位移
图2-3-5
可以想象,如果把整个运动过程划分得非常非常细,很多很多小矩形的面积之和,就能准确地代表物体的位移了。这时,“很多很多”小矩形顶端的“锯齿形”就看不出来了,这些小矩形合在一起组成了一个梯形OABC。梯形OABC的面积就代表做匀变速直线运动物体在0(此时速度是v0)到t(此时速度是v)这段时间内的位移。
在图2-3-5乙中,v-t直线下面的梯形OABC的面积是
S=(OC+AB)×OA
把面积及各条线段换成所代表的物理量,上式变成x=(v0+v)t
把前面已经得出的v=v0+at代入,得到
x=v0t+at2
这就是表示匀变速直线运动的位移与时间关系的公式。
方法点拨 注意此处空半格匀变速直线运动的位移-时间关系公式推导的方法多样,可以由匀变速直线运动的速度公式和用平均速度表示位移的公式vt=v0+at、s=(v0+vt)t得出。也可以运用速度—时间图象中的面积表示位移的方法推导,是极限思想的渗透。
2.位移和速度关系式:x=v0t+at2
公式中x表示物体在时间t内运动的位移,单位是m;v0表示初速度,单位是m/s;a表示加速度,单位是m/s2;t表示运动时间,单位是s。
深化升华 注意此处空半格
(1)反映了位移随时间的变化规律。
(2)因为v0、a、x均为矢量,使用公式时应先规定正方向。一般以v0的方向为正方向。
若a与v0同向,则a取正值;
若a与v0反向,则a取负值;
若位移计算结果为正值,说明这段时间内位移的方向为正;
若位移计算结果为负值,说明这段时间内位移的方向为负。
(3)因为位移公式是关于x的一元二次函数,故x-t图象是一条抛物线(一部分)。
3.匀变速直线运动的v-t图象
(1)特点:一条倾斜的直线。
(2)由v-t图象可以获得的信息:
①任一时刻的速度及任一速度所对应的时刻;
②某段时间内的速度变化;
③比较速度变化的快慢;(图线的倾斜程度决定速度变化的快慢)
④加速度的大小和方向:加速度的大小等于图线的斜率;斜率为正,说明加速度方向为正;斜率为负,说明加速度方向为负;
⑤某段时间内的位移。
特例:如图2-3-6
图2-3-6
初速度为负值的匀减速直线运动,位移由两部分组成:t1时刻之前位移x1为负值;t1时刻之后位移x2为正值。故在0—t2时间内总位移x=|x2|-|x1|。
若x>0,说明这段时间内物体的位移为正;
若x<0,说明这段时间内物体的位移为负。
三、匀变速直线运动的位移与速度的关系
1.位移和速度关系式:vt2-v02=2as
公式中vt表示末速度,单位是m/s;v0表示初速度,单位是 m/s;a表示加速度,单位是m/s2;s表示物体在时间t内运动的位移,单位是m。
方法点拨 注意此处空半格可以由匀变速直线运动的速度公式和位移公式:vt=v0+at,x=v0t+at2,消去时间t,得vt2-v02=2as。
2.应用
关系式中直接表明了初速度、末速度、加速度和位移之间的关系,不含时间t,在已知条件和所求的结果都不涉及时间t的问题中,应用这个关系式是较方便的,就可考虑使用。代入数据时,注意各物理量的单位要统一。
深化升华 注意此处空半格在匀速直线运动中,已知速度、时间、位移这三个物理量中的任意两个,就可以求出第三个。熟练掌握公式的变换和单位的换算是解题成功的关键,特别是速度单位的换算一定要细心、准确。代公式计算时,单位要统一。
问题·自主·探究
问题1 中央电视台新闻联播曾播出题目为“但愿比翼飞,互相不干扰”的新闻报道。报道称:人类是从鸟的飞行中受到启发而制造出飞机的。但现在由于飞机在起飞和降落过程中,经常和栖息在机场附近的飞鸟相撞而导致“机毁鸟亡”。单就美国来说,由于美国的军用机场大多建在海边,近几十年来因飞机和鸟类相撞而造成“机毁鸟亡”的事故就有300多起。鸟类撞伤飞机的事件时有发生,撞死的施鸟不计其数。因此各机场不得不耗费大量的人力、物力寻求尽可能的方法来驱赶机场附近的飞鸟。
假设某战斗机的起飞速度为50 m/s,在起飞时与一长度为10 cm的鸟相撞,把鸟撞成薄饼状,则在撞击过程中,飞鸟的加速度约为多少?
思路:设小鸟的初速度为0,末速度为战斗机的速度,位移为10 cm,根据:v2-v02=2ax求出加速度。
探究:v0=0,v=50 m/s,x=0.10 m,由v2-v02=2ax可求出飞鸟的加速度为a=1.25×104 m/s2。
问题2 有一架U2高空侦察机正以300 m/s的速度向某城市飞来,它将通过该城市上空的A点。某导弹基地离A点的距离约为9 km,设导弹以80 m/s2的加速度作匀加速直线运动,要想在A点击中敌机,当敌机离A点多远时,开始发射导弹?
思路:先求出导弹运动到A点时间,再根据时间求出敌机到A点的距离。
探究:根据x=v0t+at2,因为v0=0
所以t=s=15 s
x1=v1t=300×15 m=4 500 m。
典题·热题·新题
【例1】 一个做匀加速直线运动的物体,在前4 s内经过的位移为24 m,在第2个4 s内经过的位移是60 m,求这个物体的加速度和初速度各是多少
解析:解法一:基本公式法:
前4 s内的位移:x1=v0t+at2
第2个4 s内的位移:x2=v0(2t)+a(2t2)-(v0t+at2)
将x1=24 m、x2=60 m代入上式,解得a=2.25 m/s2,v0=1.5 m/s.
解法二:物体在8 s内的平均速度等于中间时刻(即第4 s末)的瞬时速度,则v4= m/s=v0+4a
物体在前4 s内的平均速度等于第2 s末的瞬时速度:v2= m/s=v0+2a
由两式联立,得a=2.25 m/s2,v0=1.5 m/s.
解法三:由公式Δx=aT2,得:a== m/s2=2.25 m/s2
根据v4=m/s=v0+4a,所以v0=1.5 m/s.
答案:a=2.25 m/s2,v0=1.5 m/s
温馨提示:匀变速直线运动的规律可用多个公式描述,因而选择不同的公式,所对应的解法也不同.对一般的匀变速直线运动问题,若出现相等的时间间隔问题,就优先考虑用Δs=aT2求解.
类题演练
有一个做匀变速直线运动的质点,它在两段连续相等的时间内通过的位移分别为24 m和64 m,连续相等的时间为4 s,求质点的初速度和加速度的大小.
变式提升1
一物体由静止开始做直线运动,先以加速度a1做匀加速直线运动,接着又以大小为a2的加速度做匀减速直线运动直到停止.已知通过全程所经历的时间为t,求该物体的总位移.
【例2】 枪弹在枪筒中的运动是匀加速运动,其加速度为a=5.0×105 m/s2,射出枪口的速度为vt=800 m/s,求枪筒的长x.
解析:由v2=2ax得枪筒长为:
x== m=0.64 m=64 cm.
答案:x=64 cm
温馨提示:在应用运动学公式解题时,要特别注意题目中的已知量和未知量之间的关系,选择合适的公式来解题.注意在本题中v0=0,故可用v2=2ax来求得x.
变式提升2
物体由静止开始做匀加速直线运动,当其位移为x时的速度为v,求位移为时的速度v′为多大?
【例3】 在图2-3-1中是直升机由地面起飞的速度图象,试计算直升机能到达的最大高度.25 s时直升机所在的高度是多少米?
图2-3-1
解析:首先分析直升机的运动过程:0—5 s直升机匀加速运动;5—15 s直升机匀速运动;15—20 s直升机匀减速运动;20—25 s直升机匀加速运动.分析可知直升机所能到达的最大高度为图象中梯形OABC的面积,即S1=600 m.25 s,直升机所在高度为S1与图线CE与横轴所围成的面积S△CED的差,即S2=S1-S△CED=(600-100) m=500 m.
答案:500 m
温馨提示:处理速度和时间的关系问题时,要对运动过程进行分段分析,搞清楚每一个过程的运动性质,灵活运用点、线、面、斜率和截距的物理意义.
知识拓展
1.关于图象应该强调的六字要诀:“轴”“点”“线”“斜”“截”“面”
“轴”,看清图象的坐标轴所表示的物理意义;如同一形状的图线可能表示的是位移—时间图象(v-t图象),也可能表示的是速度—时间图象,所以要看清坐标轴所表示的是哪两个量间的关系.“点”,理解图线上的点所反映的物理意义;在坐标系中,“点”往往表示某一状态,如某一时刻的位置,某一时刻的速度,某一状态的压强和体积等等.“线”,理解图线上的线段所反映的物理意义;在坐标系中,“线”往往表示一个物理过程,如某一段时间内的位移,某一段时间内的速度变化过程,某段过程中气体状态的变化经历.“斜”,求出图线的斜率,找到它所代表的物理意义;位移—时间图象中图线的斜率表示速度,速度—时间图象中图线的斜率表示加速度等等.“截”,找出图线的截距,了解它所代表的物理意义;如位移—时间图象中纵截距所表示的是初始时刻的位置,速度—时间图象中纵截距所表示的是初始时刻的速度.“面”,弄明白图线与坐标轴围成的面积表示的物理意义;如速度—时间图象中图线所围成的面积表示位移,力—位移图象中图线所围成的面积表示功等等.
2.速度图象、位移图象的对比与讨论
匀速直线运动的位移图象和匀变速直线运动的速度图象都是直线,但物理意义完全不同,如图2-3-16和2-3-17所示:
图2-3-16 图2-3-17
图2-3-16中各图线表示的运动情况如下:
①表示物体做匀速直线运动(斜率表示速度大小);
②表示物体静止;
③表示物体向反方向做匀速直线运动;
④交点的纵坐标表示物体t2时刻相遇时的位移;
⑤t1时刻物体的位移为x1.
图2-3-17中各图线表示的运动情况如下:
①表示物体做初速为零的匀加速直线运动;
②表示物体做匀速直线运动;
③表示物体做匀减速直线运动;
④交点的纵坐标表示在t2时刻物体具有相等的速度,但不相遇;
⑤t1时刻物体的速度为v1,图中阴影部分的面积表示物体①在0~t1时间内的位移.
因此在分析图象的问题时,首先要弄清该图象究竟是哪一种图象,这可以通过观察图象的纵坐标的意义来区分,这是解题的关键的一步.其次再理解图象的物理意义,分析物体的运动性质.
3.防止超速的奇招
汽车在行驶中遇到紧急情况就要刹车,学习了匀变速直线运动规律我们知道,刹车过程的长短与汽车行驶时的速度有直接的关系.高速行驶的汽车很难在短时间内刹车.在现代生活中超速驾车狂奔已成为一大公害.每分钟在全世界都有车祸发生.设计汽车的人们绞尽脑汁提高刹车性能:提高轮胎与路面的动摩擦因数,虽然收到一定效果,但车祸仍未减少.有些人就在减少汽车的行驶速度上下功夫.
马来西亚柔佛州山川秀丽,景色优美,路边竖着不少交通牌和安全标语:“阁下,驾驶汽车不超过30英里,可以饱览本地美丽景色;超过60英里,请到法庭做客;超过80英里,欢迎光临本地最先进的医院;超过100英里,请君安息吧!”文字幽默,苦口婆心,十分引人注意.
德国交通管理部门对超速行驶者不采取通常的罚金和制裁手段,而是将车扣住,停在停车场,由警察用车子把司机送到离城10千米以外的荒郊野岭,让他步行返回,以示惩戒.
墨西哥城的交通管理人员在公路边立了不少告示牌,牌上用大字写着:“请司机小心.如果超速,本城一无医院,二无医生,三无药品.”
据说,美国有一个地方,在公路拐弯处立一旗飘曳,上画一位美丽动人的年轻女郎;下写:“我喜欢开慢车.”立起这块牌子后,此处真没有出过交通事故.
北京郊区公路上常见蓝色三角标志,上画撞车图形,并写着“前方300 m处为事故多发地段”.
上述这些告示牌,言语不多,述之以理,晓之以情,使司机不要开快车.车速慢,刹车过程所用时间短,所用位移短.易于刹车,易于控制,真是减少交通事故的一种好方法.
4.位移传感器
位移传感器测运动物体的位移、速度、加速度、它由三部分组成:位移传感器、数据采集器和计算机组成.目前在中学中使用的位移传感器有两种形式.一种是超声波脉冲发射和接收装置是分离的,另一种是“雷达”式的超声波脉冲的发射与接收由一个装置实现.两者测位移的方式上略有区别.超声波脉冲发射与接收装置分开,在发射盒内单独设有电源、超声脉冲发生的振荡电路、超声脉冲发射器、红外脉冲发生与发射电路.工作时将发射系统(A盒)固定在运动物体上,A盒同时向接收装置B盒发射一个红外脉冲与一个超声波脉冲,红外脉冲是作为超声脉冲发出的计时起点,接收器B盒接收到红外脉冲开始计时,超声波冲脉到达时停止计时,再根据计时的时间差和声速计算出物体运动位移.忽略了红外线传播的时间.接收传感器B盒将接收到脉冲数与各时间差送入数据采集器,送入计算机,由专门设计的软件处理这些数据,并描绘出位移—时间图象.
位移传感器只能用于测定运动物体运的位移(距离),测物体运动的速度和加速度是通过计算机软件实现的.根据位移图线各时刻的斜率,即该时刻的瞬时速度再描绘出不同时刻的速度—时间图象,并能显示出某时刻瞬时速度值,某段时间内平均速度值.测量物体运动时的加速度则是根据速度图象在不同时刻的斜率得出,并能画出加速度与时间的图象,求物体运动的位移、速度、加速度的值,时间段可以任意选取.
第二种位移传感器将超声波脉冲的发射与接收由一个超声脉冲探头完成,在运动物体上安装反射板,将超声脉冲反射回来由传感器接收.传感器不随物体移动,也不需要发射红外脉冲作为计时起点.其时间由超声脉冲发出开始计时,至接收到反射脉冲时停止计时,以其时间的一半为计算位移的时间.装置简单,但由于反射回来的超声脉冲强度大为减弱,所以对超声波脉冲探头的灵敏度要求高,其成本也比分离式位移传感器高得多.
5.加速度计
加速度计是测定物体加速度的仪器,它应用于系统振动特性的研究,常用来测量地震.大多数地震仪都属于加速度计类型.图2-4-9为应变式加速度计示意图.
图2-4-9
当系统加速时,加速器中的敏感元件也处于加速状态中,产生加速度的外力由材料形变的回复力提供.敏感元件由弹簧悬挂在矩形支架上,支架与待测物固定,后者加速运动时一侧弹簧位伸,一侧弹簧压缩,两侧弹簧施给元件的合力即为使物块用于加速的外力.弹簧伸缩的大小与元件的加速度成正比,待测物的加速度的大小和方向由指针在标尺上示出.元件的位移也可转换为电信号输出,其强弱与元件的加速度成正比.
读书做人
最早应用极限思想解决问题的古代科学家——刘徽
刘徽是三国时代魏人,是我国古代杰出的数学奇才.他在研究、注解《九章算术》时,对圆周率进行了认真研究.为了把π取得更精确些,他使圆的内接多边形的边数增加,从而这个多边形的面积就逐渐接近圆的面积.用这种方法计算π,刘徽首先从圆的内接正六边形算起,然后边数一倍一倍地增加,这样正多边形面积就越来越接近圆的面积.如果取圆的半径r=1,那么这些正多边形的面积的数值就逐渐逼近圆周率π,按照他的说法,就是“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣”.刘徽计算到内接192边形时,得到的圆周率π=3.141 024,在实际应用时,常取π=3.14.
显然,刘徽当时已有了极限的思想,他的这种方法就是后来科学家发现科学规律经常采用的方法.他把圆看作边数无限多的正多边形,而边数有限多的正多边形面积是可求的.这样一来,就可用有限来逼近无限了.这种思考问题的方法至今还起着重大作用.刘徽在研究许多数学问题时都用到了极限的思想方法.
思考:阅读该材料,体会极限思想在解决问题时的应用.
自主广场
我夯基 我达标
1.关于匀加速直线运动,下列说法正确的是( )
A.位移与时间的平方成正比
B.位移总是随时间增加而增加
C.加速度、速度、位移三者方向一致
D.加速度、速度、位移的方向并不是都相同
解析:物体做加速运动,则速度的方向和加速度的方向相同,并且做单方向的直线运动,因此相对出发点来说,位移的方向与初速度的方向一致,C正确.
由位移公式x=v0t+at2可知,当初速度不等于零时,位移与时间的平方不成正比,只有初速度为零时才成正比.因此B正确,A不正确.
答案:BC
2.一物体做匀变速直线运动,下列说法中正确的是( )
A.物体的末速度一定与时间成正比
B.物体的位移一定与时间的平方成正比
C.物体的速度在一定时间内发生的变化与这段时间成正比
D.若为匀加速运动,速度和位移都随时间增加;若为匀减速运动,速度和位移都随时间减小
解析:根据v=v0+at和x=v0t+at2,知A、B选项不正确,由加速度公式知C正确.
当物体做匀减速运动时,速度减小但位移可以增大.
答案:C
3.汽车在平直公路上以10 m/s的速度做匀速直线运动,发现前面有情况而刹车,获得的加速度为2 m/s2.则
(1)汽车经过3 s时速度的大小为____________m/s;
(2)汽车经5 s时速度的大小是_______________;
(3)汽车经过10 s时速度的大小是______________.
解析:汽车刹车问题先要求出刹车过程的总时间,然后再讨论在不同时刻的运动情况.
由vt=v0+at可得,0=10-2t,t=5 s,即刹车时间为5 s.
汽车经3 s时速度大小v=v0+at=(10-2×3) m/s=4 m/s.
汽车经10 s时速度大小为0.
答案:(1)4 (2)0 (3)0
4.一质点做直线运动的x-t图象如图2-3-4所示,则质点在各段时间内做什么运动?
图2-3-4
解析:设质点从O点开始沿x轴运动,如图所示.在0—t1时间内,质点沿x轴正向做匀速直线运动,t1时刻到达A点;t1—t2时间内,x-t图象是一条平行于t轴的直线,位移没有变大也没有变小,即在这段时间内质点的位置未变,一直停在A点;在t2—t3时间内,x-t图象是一条倾斜的直线,质点做匀速直线运动,位移不断减小,说明质点由A点向O点运动,t3时刻到达OA之间某点B.
答案:见解析
我综合 我发展
5.一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速直线运动,接着做匀减速直线运动,开到乙地刚好停止,其速度图象如图2-3-5所示.那么0—t0和t0—3t0两段时间内( )
图2-3-5
A.加速度大小之比为3∶1 B.位移大小之比为1∶2
C.平均速度大小之比为2∶1 D.平均速度大小之比为1∶1
解析:在v-t图象中,加速度的大小可以根据直线的斜率求得,而位移的大小可以根据图象和坐标轴所围的面积求得.平均速度可以根据v=x/t求得.
可得:0—t0和t0—3t0两段时间内,加速度大小之比为2∶1,位移大小之比为1∶2,平均速度大小之比为1∶1.
答案:BD
6.两辆完全相同的汽车,沿平直路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住后,后车以前车刹车时的加速度开始刹车.已知前车在刹车过程中行驶的距离为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少为( )
A.s B.2s C.3s D.4s
解析:以前车为参考系,后车相当于先以初速度为0、加速度为a做匀加速直线运动,后以同样大小的加速度a做匀减速直线运动,而后通过的位移即两车匀速行驶的距离.因此s总=at2+at2.已知前车在刹车过程中行驶的距离为s,则at2=s,所以s总=2s.
答案:B
7.(2006广东高考A卷,2)a、b两物体从同一位置沿同一直线运动,它们的速度图象如图2-3-6所示,下列说法正确的是( )
图2-3-6
A.a、b加速时,物体a的加速度大于物体b的加速度
B.20秒时,a、b两物体相距最远
C.60秒时,物体a在物体b的前方
D.40秒时,a、b两物体速度相等,相距200 m
解析:v-t图象上直线的斜率反映加速度的大小,所以b的加速度大于a的加速度,A错;20秒时,a、b相距500 m,不是最远的,而是二者速度相等时相距最远,60秒时a的位移大于b的位移,所以a在b的前方,C对;40秒时,a、b速度相等,相距最远,相距500 m,所以D错.
答案:C
8.一辆巡逻车最快能在10 s内由静止加速到最高速度50 m/s,并能保持这个速度匀速行驶,问该巡逻车在平直的高速公路上由静止追上前方2 000 m处正以35 m/s的速度匀速行驶的汽车,至少需要多长时间?(巡逻车加速过程,加速度恒定)
解析:巡逻车以最大加速度加速,以最高速度行驶时所用的时间最短,设追及所需最短时间为t,则在这段时间内汽车行驶了s1=v1t,巡逻车加速过程行驶了s2=t0
匀速行驶了s3=v2(t-t0),追及时:s2+s3=s0+s1,即
v0t0+v2(t-t0)=s0+v1t
所以t=150 s.
答案:150 s
我创新 我超越
9.有种理论认为百慕大三角区之谜是水合天然气引起的.在海底,由于温度低、压力大,动植物遗体腐烂变成天然气与水结合,形成了固态的水合天然气.这些水合天然气稳定的条件一旦受到破坏,就可分解出气态的天然气气泡上升,上升的气泡流导致海底的压力变小,更多的固态水合天然气汽化.这样导致大量天然气溢出海面.大量的天然气气泡使海水的密度变小,浮力下降,当船舶驶入这个区域时,海水浮力支撑不住船舶的重力,而使船舶沉入海底.飞机飞入这个地带,则可引燃天然气,而被烧毁坠入海中.
一艘水上排水量为900 t、水下排水量为1 200 t、最大潜水深度为250 m的潜水艇在该地区海面下100 m处巡航,突然海水密度骤降(假如潜艇所在处及它下面海水密度从1.03×103 kg/m3骤变为0.9×103 kg/m3),5 s后潜艇发现此情况并立即采取措施,以最快的速度排泄艇内贮水舱中的水,当它刚止住自己加速下坠时已在水面下200 m处,不计阻力.试分析:
(1)潜水艇在采取措施前的5 s内下坠了多大距离?这时它的速度是多少?
(2)假如潜水艇一直保持排水速度不变,它做什么运动?加速度大小如何变化?能否摆脱葬身海底的厄运?
答案:略
更上一层楼
基础·巩固·达标
1.如图2-3-9所示为甲、乙两物体的x-t图象,则( )
图2-3-9
A.甲、乙两物体都做匀速直线运动
B.若甲、乙两物体在同一直线上运动,则一定会相遇
C.t1时刻甲、乙相遇
D.t2时刻甲、乙相遇
解析:本题考查物体的x-t图象,由图象可知甲、乙两物体都做匀速直线运动,但甲的位移增大,而乙的位移不断减小,甲乙两物体的运动方向相反,但都做匀速直线运动。
答案:ABC
2.一辆汽车以10 m/s的速度沿平直公路匀速运动,司机发现前方有障碍物立即减速,以0.2 m/s2的加速度做匀减速运动,减速后一分钟内汽车的位移为( )
A.240 m B.250 C.260 m D.90 m
解析:当t=50 s时汽车停止运动,所以x=m=250 m。
答案:B
3.一质点沿Ot坐标轴运动,t=0时,位于坐标原点,图2-3-10为质点做直线运动的速度—时间图象。由图可知
图2-3-10
(1)该质点的位移随时间变化的关系式是x=______________;
(2)在时间t=_____________s时质点距坐标原点最远;
(3)从t=0到t=20 s内质点的位移是_____________,通过的路程是_____________。
解析:由图象可知v0=-4 m/s,斜率为0.4,则x=v0t+at2=-4t+0.2t2,物体10 s前沿负方向运动,10 s后返回,所以10 s时距原点最远。20 s时返回原点,位移为0,路程为40 m。
答案:(1)-4t+0.2t2 (2)10 (3)0 40 m
4.物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2 m,BC=3 m,CD=4 m,且物体通过AB、BC、CD所用的时间相等,则OA之间的距离为_________________m(如图2-3-11)。
图2-3-11
解析:本题考查位移公式、速度公式、位移速度关系式的综合应用。怎样选择公式去解题,是解答这类问题的关键。
设时间间隔为t,则vB=,所以a=,OA=OB-AB=-2 m=1.125 m。
答案:1.125
5.有一个做匀加速直线运动的质点,它在开始的两个连续相等的时间间隔内所通过的路程分别是24 m和64 m,每一时间间隔为4 s。则质点运动的初速度和加速度分别为___________m/s和__________m/s2。
解析:物体开始运动4 s后的瞬时速度v==(24+64)/8 m/s=11 m/s,所以x1=·t,即v0=-11 m/s=1 m/s,又因为x1=v0·t+at2,所以a=2.5 m/s2。
答案:1 2.5
6如图2-3-12所示,为一直升机垂直起飞过程的v-t图象,则直升机运动中有几个不同性质的过程,计算飞机能到达的最大的高度?25 s时飞机的高度是多少?
图2-3-12
解:由v-t图象的意义得0—5 s内匀加速,5—15 s内匀速;
15—20 s内匀减速;0—20 s内速度方向一直向上,
20—25 s内向下匀加速,速度是负值,
可知,当20 s时竖直向上的位移最大。位移的大小为图线与坐标轴围成的“面积”:
s=×40 m=600 m
当20 s到25 s阶段飞机向下运动:
s1= m=200 m
因此,25 s时飞机的高度为400 m。
7.火车沿平直铁轨匀加速前进,通过某一路标时的速度为10.8 km/h,1 min后变成 54 km/h,再经一段时间,火车的速度达到 64.8 km/h。求所述过程中,火车的位移是多少。
解:火车一直做匀加速运动,其位移可由多种不同方法求解。
解法1:整个过程的平均速度:=m=m/s
时间t=75 s,则火车位移:x==×75 m=787.5 m
解法2:由x=v0·t+at2得位移x=3×75+×0.2×52=787.5 m。
8.一块木板厚为d=10 mm,子弹垂直板面穿过木板,已知穿透前后子弹的速度分别为v1=50 m/s和v2=30 m/s,求穿透所用时间是多少。
解析:本题考查速度、位移关系的公式的掌握,注意在应用公式时,要选取正方向。
解:d==·t,即10×10-3 s=·t,解得t=2.5×10-4 s。
9.汽车做匀加速直线运动,由A到B和由B到C所用时间均是2 s,且前2 s和后2 s的位移分别为8 m、12 m,求汽车运动的加速度和初速度、末速度。
解析:本题考查速度公式、位移公式的综合应用,在解答题目的过程中,要注意灵活选用适当的公式,尽量使解题过程简单些。
解:vB==m/s=5 m/s,xAB=·t,
vA=3 m/s,xBC=·t,所以vC=7 m/s,a==1 m/s2。
10.汽车以54 km/h的速度在水平路面上运动,紧急刹车后,以7.5 m/s2的加速度做匀减速直线运动。求汽车刹车后3 s内车的位移。
解:54 km/h=15 m/s,当汽车以v0=15 m/s的初速度、7.5 m/s2的加速度匀减速行驶时,根据速度公式:vt=v0+at得t==2 s,经过2 s汽车就停止运动,所以汽车刹车后3 s内的位移与2 s内的位移是相等的,位移大小为x=v0t+at2=15 m/s×2 s-×7.5 m/s2×(2 s)2=15 m,或者根据公式:v02=2ax得x=m=15 m。
综合·应用·创新
11.两辆完全相同的汽车,沿平直路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住后,后车以前车刹车时的加速度开始刹车。已知前车在刹车过程中行驶的距离为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少为( )
A.s B.2s C.3s D.4s
解析:以前车为参考系,后车相当于先以初速度为0,加速度为a做匀加速直线运动,后以同样大小的加速度a做匀减速直线运动,而后撤通过的位移即两车匀速行驶时距离。因此 s总=at2+at2。已知前车在刹车过程中行驶的距离为s,则at2=s,所以 s总=2s。
答案:B
12.据国外报道,科学家正在研制一种可以发射小型人造卫星的超级大炮。它能够将一个体积约为2 m3(底面面积约为0.8 m2)、质量为400 kg的人造卫星从大炮中以300 m/s的速度发射出去,再加上辅助火箭的推进,最终将卫星送入轨道。发射部分有长650 m左右的加速管道,内部分隔成许多气室,当卫星每进入一个气室,该气室的甲烷、空气混合气体便点燃产生推力,推动卫星加速,其加速度可以看作是恒定的。则这种大炮的加速度的大小约为____________m/s2。
解析:人造卫星在大炮中的初速度v0=0,末速度为v1=300 m/s,加速的位移为s=650 m,由公式vt2=2as,得a=m/s2=69.2 m/s2。
答案:69.2
13.质点由静止开始以1.2 m/s2的加速度做匀加速直线运动,经过10 s后,改做匀速直线运动,又经5 s,接着做匀减速直线运动,再经过20 s停止。求:
(1)质点做匀速直线运动的速度大小和匀减速直线运动的加速度;
(2)整个过程中运动的位移大小。
解:(1)加速10 s运动的位移x1=1/2a1t12=60 m。
10 s末的速度v1=a1t1=12 m/s
匀速运动的位移x2=v1t2=60 m
减速过程中0=v1+a2t3,a2=-0.6 m/s2,x3=120 m。
(2)x=x1+x2+x3=240 m。
14.一辆巡逻车最快能在10 s内由静止加速到最高速度50 m/s,并能保持这个速度匀速行驶,问该巡逻车在平直的高速公路上由静止追上前方2 000 m处正以35 m/s的速度匀速行驶的汽车,至少需要多长时间?(巡逻车加速过程,加速度恒定)
解:巡逻车以最大加速度加速,以最高速度行驶时所用的时间最短,设追及所需最短时间为t,则在这段时间内汽车行驶了 s1=v1t。巡逻车加速过程行驶了 s2=。
匀速行驶了 s3=v2(t-t0),追及时: s2+ s3= s0+ s1。即
()v0t0+v2(t-t0)= s0+v1t
所以t=150 s。
15.如图2-3-13所示,在国庆阅兵式中,某直升机在地面上空某高度A处静止待命,要求该机10 h 56 min 40 s从静止状态沿水平方向做匀加速直线运动,经过AB段加速后,进入BC段的匀速受阅区,11时准时通过C位置,已知sAB=5 km,sBC=10 km。问:
图2-3-13
(1)直升机在BC段的速度为多大
(2)在AB段做匀加速运动的加速度为多大
解:(1)由题意知,飞机由A到B为匀加速直线运动,由B到C为匀速直线运动,共用时间3 min 20 s,即t=200 s。设匀速运动时的速度为v,AB段所用时间为t1,BC段所用时间为t2,则vt1=sAB=5 000 m, vt2=sBC=10 000 m,t1+t2=200 s,几个公式联立得v=100 m/s。
t1=t2=100 s。
(2)设AB段匀加速的加速度为a,则v=at1,a=1=1 m/s2。
16.在高速公路上,有时会发生“追尾”的事故——后面的汽车撞上前面的汽车。请分析一下,造成“追尾”事故的原因有哪些 我国高速公路的最高车速限制为120 km/h。设某人驾车正以最高时速沿平直高速公路行驶,该车刹车时产生的加速度大小为5 m/s2,司机的反应时间(从意识到应该停车至操作刹车的时间)为0.6—0.7 s。请分析一下,应该如何计算行驶时的安全车距
解析:从后车的运动考虑,造成“追尾”的原因主要有以下几方面:(1)车速过快;(2)跟前车的车距过小;(3)司机的反应较迟缓;(4)车的制动性能较差。
解:当司机发现紧急情况(如前方车辆突然停下)后,在反应时间内,汽车仍以原来的速度做匀速直线运动;刹车后,汽车匀减速滑行。所以,刹车过程中汽车先后做着两种不同的运动,行驶时的安全车距应等于两部分位移之和。其运动情况如上图所示。为确保安全行车,反应时间应取0.7 s计算。
汽车原来的速度v0=120 km/h=33.3 m/s。在反应时间t1=0.7 s内,汽车做匀速直线运动的位移为 s1=v0t1=33.3×0.7 m=23.3 m。刹车后,汽车做匀减速运动,滑行时间为t2=s=6.7 s,汽车刹车后滑行的位移为 s2=v0t+at2=110.9 m,所以行驶时
的安全车距应为 s= s1+ s2=23.3 m+110.9 m=134.2 m。
情景导入
鸟击落飞机
中央电视台新闻联播中播出题目为:“但愿比翼飞,互相不干扰”的新闻报道.报道称:人类是从鸟的飞行中受到启发而制造出飞机的,但现在由于飞机在起飞和降落过程中,经常和栖息在机场附近的飞鸟相撞而导致“机毁鸟亡”,美国就发生此类事故300多起,致使各机场不得不耗费大量的人力、物力来驱赶机场附近的飞鸟.
假设某战斗机的起飞速度为50 m/s,在起飞时与一长度为10 cm的鸟相撞,把鸟撞成薄饼状贴在飞机上,则在撞机过程中,飞鸟的加速度约为多大
简答:战斗机的起飞速度为50 m/s,飞鸟忽略不计,由匀变速直线运动的位移与速度的关系式v2-v02=2ax,得飞鸟的加速度约为12 500 m/s2.
新知预习
匀速直线运动中的位移:对应着v-t图象中 .?
匀变速直线运动的位移:对应着v-t图象中 围成的面积.从此推导出的位移公式为: .?
匀变速直线运动的位移与速度的关系:v2-v02=2ax.
知识·巧学·升华
一、匀速直线运动的位移
1.匀速直线运动是物体沿一条直线运动,且速度保持不变的运动。它的特点是v大小方向都不变,位移x跟发生这段位移所用的时间t成正比。
2.位移公式:x=v-t。
3.匀速直线运动的v-t图象
(1)特点:图线与时间轴平行。
(2)由v-t图象可以获得的信息:
①任一时刻的速度大小和方向:若速度为正值,则图线位于时间轴上方;若速度为负值,则图线位于时间轴下方;若物体静止,则图线与时间轴重合。
②任一段时间内的位移:等于时间轴、速度图线、这段时间的初末时刻所包围的一块矩形的面积。若速度为正,则所包围的矩形位于时间轴的上方(如图2-3-1),说明这段位移的方向为正;若速度为负,则所包围的矩形位于时间轴的下方(图2-3-2),说明这段位移的方向为负。
向正方向的匀速直线运动 向负方向的匀速直线运动
图2-3-1 图2-3-2
4.匀速直线运动的x-t图象
图2-3-3
(1)特点:是一条倾斜直线。如图2-3-3。
(2)图象的含义
①表明在匀速直线运动中,x∝t。
②图象上任一点的横坐标表示运动的时间,对应的纵坐标表示位移。
③图象的斜率k=Δx/Δt=v。
二、匀变速直线运动的位移
1.匀变速直线运动的位移公式的推导
物体运动的v-t图象如图2-3-4甲所示。
某物体以初速 每两个位置间的位移正好等于以
度v0做匀变速直线 t为底、以速度为高的
运动的速度—时间图象 细高矩形的面积。矩形面积之
和,可以精略地表示整个运动过程的位移
图2-3-4
先把物体的运动分成几个小段,例如t算一个小段,在v-t图中,每小段起始时刻物体的瞬时速度由相应的纵坐标表示(图2-3-4乙)。我们以每小段起始时刻的速度乘以时间t近似地当作各小段中物体的位移,各段位移可以用一个又窄又高的小矩形的面积代表。5个小矩形的面积之和近似地代表物体在整个过程中的位移。
当然,上面的做法是粗糙的。为了精确一些,可以把运动过程划分为更多的小段,如图2-3-5甲,用所有这些小段的位移之和,近似代表物体在整个过程中的位移。从v-t图上看,就是用更多的但是更窄的小矩形的面积之和代表物体的位移。
甲 乙
如果各位置的时间间隔小一些, 如果时间分得非常细,小矩形就会非常多,
这些矩形面积之和就能比较精确 它们的面积就等于CB斜线下的面积,可十
地代表整个运动的位移 分准确地代表整个运动的位移
图2-3-5
可以想象,如果把整个运动过程划分得非常非常细,很多很多小矩形的面积之和,就能准确地代表物体的位移了。这时,“很多很多”小矩形顶端的“锯齿形”就看不出来了,这些小矩形合在一起组成了一个梯形OABC。梯形OABC的面积就代表做匀变速直线运动物体在0(此时速度是v0)到t(此时速度是v)这段时间内的位移。
在图2-3-5乙中,v-t直线下面的梯形OABC的面积是
S=(OC+AB)×OA
把面积及各条线段换成所代表的物理量,上式变成x=(v0+v)t
把前面已经得出的v=v0+at代入,得到
x=v0t+at2
这就是表示匀变速直线运动的位移与时间关系的公式。
方法点拨 注意此处空半格匀变速直线运动的位移-时间关系公式推导的方法多样,可以由匀变速直线运动的速度公式和用平均速度表示位移的公式vt=v0+at、s=(v0+vt)t得出。也可以运用速度—时间图象中的面积表示位移的方法推导,是极限思想的渗透。
2.位移和速度关系式:x=v0t+at2
公式中x表示物体在时间t内运动的位移,单位是m;v0表示初速度,单位是m/s;a表示加速度,单位是m/s2;t表示运动时间,单位是s。
深化升华 注意此处空半格
(1)反映了位移随时间的变化规律。
(2)因为v0、a、x均为矢量,使用公式时应先规定正方向。一般以v0的方向为正方向。
若a与v0同向,则a取正值;
若a与v0反向,则a取负值;
若位移计算结果为正值,说明这段时间内位移的方向为正;
若位移计算结果为负值,说明这段时间内位移的方向为负。
(3)因为位移公式是关于x的一元二次函数,故x-t图象是一条抛物线(一部分)。
3.匀变速直线运动的v-t图象
(1)特点:一条倾斜的直线。
(2)由v-t图象可以获得的信息:
①任一时刻的速度及任一速度所对应的时刻;
②某段时间内的速度变化;
③比较速度变化的快慢;(图线的倾斜程度决定速度变化的快慢)
④加速度的大小和方向:加速度的大小等于图线的斜率;斜率为正,说明加速度方向为正;斜率为负,说明加速度方向为负;
⑤某段时间内的位移。
特例:如图2-3-6
图2-3-6
初速度为负值的匀减速直线运动,位移由两部分组成:t1时刻之前位移x1为负值;t1时刻之后位移x2为正值。故在0—t2时间内总位移x=|x2|-|x1|。
若x>0,说明这段时间内物体的位移为正;
若x<0,说明这段时间内物体的位移为负。
三、匀变速直线运动的位移与速度的关系
1.位移和速度关系式:vt2-v02=2as
公式中vt表示末速度,单位是m/s;v0表示初速度,单位是 m/s;a表示加速度,单位是m/s2;s表示物体在时间t内运动的位移,单位是m。
方法点拨 注意此处空半格可以由匀变速直线运动的速度公式和位移公式:vt=v0+at,x=v0t+at2,消去时间t,得vt2-v02=2as。
2.应用
关系式中直接表明了初速度、末速度、加速度和位移之间的关系,不含时间t,在已知条件和所求的结果都不涉及时间t的问题中,应用这个关系式是较方便的,就可考虑使用。代入数据时,注意各物理量的单位要统一。
深化升华 注意此处空半格在匀速直线运动中,已知速度、时间、位移这三个物理量中的任意两个,就可以求出第三个。熟练掌握公式的变换和单位的换算是解题成功的关键,特别是速度单位的换算一定要细心、准确。代公式计算时,单位要统一。
问题·自主·探究
问题1 中央电视台新闻联播曾播出题目为“但愿比翼飞,互相不干扰”的新闻报道。报道称:人类是从鸟的飞行中受到启发而制造出飞机的。但现在由于飞机在起飞和降落过程中,经常和栖息在机场附近的飞鸟相撞而导致“机毁鸟亡”。单就美国来说,由于美国的军用机场大多建在海边,近几十年来因飞机和鸟类相撞而造成“机毁鸟亡”的事故就有300多起。鸟类撞伤飞机的事件时有发生,撞死的施鸟不计其数。因此各机场不得不耗费大量的人力、物力寻求尽可能的方法来驱赶机场附近的飞鸟。
假设某战斗机的起飞速度为50 m/s,在起飞时与一长度为10 cm的鸟相撞,把鸟撞成薄饼状,则在撞击过程中,飞鸟的加速度约为多少?
思路:设小鸟的初速度为0,末速度为战斗机的速度,位移为10 cm,根据:v2-v02=2ax求出加速度。
探究:v0=0,v=50 m/s,x=0.10 m,由v2-v02=2ax可求出飞鸟的加速度为a=1.25×104 m/s2。
问题2 有一架U2高空侦察机正以300 m/s的速度向某城市飞来,它将通过该城市上空的A点。某导弹基地离A点的距离约为9 km,设导弹以80 m/s2的加速度作匀加速直线运动,要想在A点击中敌机,当敌机离A点多远时,开始发射导弹?
思路:先求出导弹运动到A点时间,再根据时间求出敌机到A点的距离。
探究:根据x=v0t+at2,因为v0=0
所以t=s=15 s
x1=v1t=300×15 m=4 500 m。
典题·热题·新题
【例1】 一个做匀加速直线运动的物体,在前4 s内经过的位移为24 m,在第2个4 s内经过的位移是60 m,求这个物体的加速度和初速度各是多少
解析:解法一:基本公式法:
前4 s内的位移:x1=v0t+at2
第2个4 s内的位移:x2=v0(2t)+a(2t2)-(v0t+at2)
将x1=24 m、x2=60 m代入上式,解得a=2.25 m/s2,v0=1.5 m/s.
解法二:物体在8 s内的平均速度等于中间时刻(即第4 s末)的瞬时速度,则v4= m/s=v0+4a
物体在前4 s内的平均速度等于第2 s末的瞬时速度:v2= m/s=v0+2a
由两式联立,得a=2.25 m/s2,v0=1.5 m/s.
解法三:由公式Δx=aT2,得:a== m/s2=2.25 m/s2
根据v4=m/s=v0+4a,所以v0=1.5 m/s.
答案:a=2.25 m/s2,v0=1.5 m/s
温馨提示:匀变速直线运动的规律可用多个公式描述,因而选择不同的公式,所对应的解法也不同.对一般的匀变速直线运动问题,若出现相等的时间间隔问题,就优先考虑用Δs=aT2求解.
类题演练
有一个做匀变速直线运动的质点,它在两段连续相等的时间内通过的位移分别为24 m和64 m,连续相等的时间为4 s,求质点的初速度和加速度的大小.
变式提升1
一物体由静止开始做直线运动,先以加速度a1做匀加速直线运动,接着又以大小为a2的加速度做匀减速直线运动直到停止.已知通过全程所经历的时间为t,求该物体的总位移.
【例2】 枪弹在枪筒中的运动是匀加速运动,其加速度为a=5.0×105 m/s2,射出枪口的速度为vt=800 m/s,求枪筒的长x.
解析:由v2=2ax得枪筒长为:
x== m=0.64 m=64 cm.
答案:x=64 cm
温馨提示:在应用运动学公式解题时,要特别注意题目中的已知量和未知量之间的关系,选择合适的公式来解题.注意在本题中v0=0,故可用v2=2ax来求得x.
变式提升2
物体由静止开始做匀加速直线运动,当其位移为x时的速度为v,求位移为时的速度v′为多大?
【例3】 在图2-3-1中是直升机由地面起飞的速度图象,试计算直升机能到达的最大高度.25 s时直升机所在的高度是多少米?
图2-3-1
解析:首先分析直升机的运动过程:0—5 s直升机匀加速运动;5—15 s直升机匀速运动;15—20 s直升机匀减速运动;20—25 s直升机匀加速运动.分析可知直升机所能到达的最大高度为图象中梯形OABC的面积,即S1=600 m.25 s,直升机所在高度为S1与图线CE与横轴所围成的面积S△CED的差,即S2=S1-S△CED=(600-100) m=500 m.
答案:500 m
温馨提示:处理速度和时间的关系问题时,要对运动过程进行分段分析,搞清楚每一个过程的运动性质,灵活运用点、线、面、斜率和截距的物理意义.
知识拓展
1.关于图象应该强调的六字要诀:“轴”“点”“线”“斜”“截”“面”
“轴”,看清图象的坐标轴所表示的物理意义;如同一形状的图线可能表示的是位移—时间图象(v-t图象),也可能表示的是速度—时间图象,所以要看清坐标轴所表示的是哪两个量间的关系.“点”,理解图线上的点所反映的物理意义;在坐标系中,“点”往往表示某一状态,如某一时刻的位置,某一时刻的速度,某一状态的压强和体积等等.“线”,理解图线上的线段所反映的物理意义;在坐标系中,“线”往往表示一个物理过程,如某一段时间内的位移,某一段时间内的速度变化过程,某段过程中气体状态的变化经历.“斜”,求出图线的斜率,找到它所代表的物理意义;位移—时间图象中图线的斜率表示速度,速度—时间图象中图线的斜率表示加速度等等.“截”,找出图线的截距,了解它所代表的物理意义;如位移—时间图象中纵截距所表示的是初始时刻的位置,速度—时间图象中纵截距所表示的是初始时刻的速度.“面”,弄明白图线与坐标轴围成的面积表示的物理意义;如速度—时间图象中图线所围成的面积表示位移,力—位移图象中图线所围成的面积表示功等等.
2.速度图象、位移图象的对比与讨论
匀速直线运动的位移图象和匀变速直线运动的速度图象都是直线,但物理意义完全不同,如图2-3-16和2-3-17所示:
图2-3-16 图2-3-17
图2-3-16中各图线表示的运动情况如下:
①表示物体做匀速直线运动(斜率表示速度大小);
②表示物体静止;
③表示物体向反方向做匀速直线运动;
④交点的纵坐标表示物体t2时刻相遇时的位移;
⑤t1时刻物体的位移为x1.
图2-3-17中各图线表示的运动情况如下:
①表示物体做初速为零的匀加速直线运动;
②表示物体做匀速直线运动;
③表示物体做匀减速直线运动;
④交点的纵坐标表示在t2时刻物体具有相等的速度,但不相遇;
⑤t1时刻物体的速度为v1,图中阴影部分的面积表示物体①在0~t1时间内的位移.
因此在分析图象的问题时,首先要弄清该图象究竟是哪一种图象,这可以通过观察图象的纵坐标的意义来区分,这是解题的关键的一步.其次再理解图象的物理意义,分析物体的运动性质.
3.防止超速的奇招
汽车在行驶中遇到紧急情况就要刹车,学习了匀变速直线运动规律我们知道,刹车过程的长短与汽车行驶时的速度有直接的关系.高速行驶的汽车很难在短时间内刹车.在现代生活中超速驾车狂奔已成为一大公害.每分钟在全世界都有车祸发生.设计汽车的人们绞尽脑汁提高刹车性能:提高轮胎与路面的动摩擦因数,虽然收到一定效果,但车祸仍未减少.有些人就在减少汽车的行驶速度上下功夫.
马来西亚柔佛州山川秀丽,景色优美,路边竖着不少交通牌和安全标语:“阁下,驾驶汽车不超过30英里,可以饱览本地美丽景色;超过60英里,请到法庭做客;超过80英里,欢迎光临本地最先进的医院;超过100英里,请君安息吧!”文字幽默,苦口婆心,十分引人注意.
德国交通管理部门对超速行驶者不采取通常的罚金和制裁手段,而是将车扣住,停在停车场,由警察用车子把司机送到离城10千米以外的荒郊野岭,让他步行返回,以示惩戒.
墨西哥城的交通管理人员在公路边立了不少告示牌,牌上用大字写着:“请司机小心.如果超速,本城一无医院,二无医生,三无药品.”
据说,美国有一个地方,在公路拐弯处立一旗飘曳,上画一位美丽动人的年轻女郎;下写:“我喜欢开慢车.”立起这块牌子后,此处真没有出过交通事故.
北京郊区公路上常见蓝色三角标志,上画撞车图形,并写着“前方300 m处为事故多发地段”.
上述这些告示牌,言语不多,述之以理,晓之以情,使司机不要开快车.车速慢,刹车过程所用时间短,所用位移短.易于刹车,易于控制,真是减少交通事故的一种好方法.
4.位移传感器
位移传感器测运动物体的位移、速度、加速度、它由三部分组成:位移传感器、数据采集器和计算机组成.目前在中学中使用的位移传感器有两种形式.一种是超声波脉冲发射和接收装置是分离的,另一种是“雷达”式的超声波脉冲的发射与接收由一个装置实现.两者测位移的方式上略有区别.超声波脉冲发射与接收装置分开,在发射盒内单独设有电源、超声脉冲发生的振荡电路、超声脉冲发射器、红外脉冲发生与发射电路.工作时将发射系统(A盒)固定在运动物体上,A盒同时向接收装置B盒发射一个红外脉冲与一个超声波脉冲,红外脉冲是作为超声脉冲发出的计时起点,接收器B盒接收到红外脉冲开始计时,超声波冲脉到达时停止计时,再根据计时的时间差和声速计算出物体运动位移.忽略了红外线传播的时间.接收传感器B盒将接收到脉冲数与各时间差送入数据采集器,送入计算机,由专门设计的软件处理这些数据,并描绘出位移—时间图象.
位移传感器只能用于测定运动物体运的位移(距离),测物体运动的速度和加速度是通过计算机软件实现的.根据位移图线各时刻的斜率,即该时刻的瞬时速度再描绘出不同时刻的速度—时间图象,并能显示出某时刻瞬时速度值,某段时间内平均速度值.测量物体运动时的加速度则是根据速度图象在不同时刻的斜率得出,并能画出加速度与时间的图象,求物体运动的位移、速度、加速度的值,时间段可以任意选取.
第二种位移传感器将超声波脉冲的发射与接收由一个超声脉冲探头完成,在运动物体上安装反射板,将超声脉冲反射回来由传感器接收.传感器不随物体移动,也不需要发射红外脉冲作为计时起点.其时间由超声脉冲发出开始计时,至接收到反射脉冲时停止计时,以其时间的一半为计算位移的时间.装置简单,但由于反射回来的超声脉冲强度大为减弱,所以对超声波脉冲探头的灵敏度要求高,其成本也比分离式位移传感器高得多.
5.加速度计
加速度计是测定物体加速度的仪器,它应用于系统振动特性的研究,常用来测量地震.大多数地震仪都属于加速度计类型.图2-4-9为应变式加速度计示意图.
图2-4-9
当系统加速时,加速器中的敏感元件也处于加速状态中,产生加速度的外力由材料形变的回复力提供.敏感元件由弹簧悬挂在矩形支架上,支架与待测物固定,后者加速运动时一侧弹簧位伸,一侧弹簧压缩,两侧弹簧施给元件的合力即为使物块用于加速的外力.弹簧伸缩的大小与元件的加速度成正比,待测物的加速度的大小和方向由指针在标尺上示出.元件的位移也可转换为电信号输出,其强弱与元件的加速度成正比.
读书做人
最早应用极限思想解决问题的古代科学家——刘徽
刘徽是三国时代魏人,是我国古代杰出的数学奇才.他在研究、注解《九章算术》时,对圆周率进行了认真研究.为了把π取得更精确些,他使圆的内接多边形的边数增加,从而这个多边形的面积就逐渐接近圆的面积.用这种方法计算π,刘徽首先从圆的内接正六边形算起,然后边数一倍一倍地增加,这样正多边形面积就越来越接近圆的面积.如果取圆的半径r=1,那么这些正多边形的面积的数值就逐渐逼近圆周率π,按照他的说法,就是“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣”.刘徽计算到内接192边形时,得到的圆周率π=3.141 024,在实际应用时,常取π=3.14.
显然,刘徽当时已有了极限的思想,他的这种方法就是后来科学家发现科学规律经常采用的方法.他把圆看作边数无限多的正多边形,而边数有限多的正多边形面积是可求的.这样一来,就可用有限来逼近无限了.这种思考问题的方法至今还起着重大作用.刘徽在研究许多数学问题时都用到了极限的思想方法.
思考:阅读该材料,体会极限思想在解决问题时的应用.
自主广场
我夯基 我达标
1.关于匀加速直线运动,下列说法正确的是( )
A.位移与时间的平方成正比
B.位移总是随时间增加而增加
C.加速度、速度、位移三者方向一致
D.加速度、速度、位移的方向并不是都相同
解析:物体做加速运动,则速度的方向和加速度的方向相同,并且做单方向的直线运动,因此相对出发点来说,位移的方向与初速度的方向一致,C正确.
由位移公式x=v0t+at2可知,当初速度不等于零时,位移与时间的平方不成正比,只有初速度为零时才成正比.因此B正确,A不正确.
答案:BC
2.一物体做匀变速直线运动,下列说法中正确的是( )
A.物体的末速度一定与时间成正比
B.物体的位移一定与时间的平方成正比
C.物体的速度在一定时间内发生的变化与这段时间成正比
D.若为匀加速运动,速度和位移都随时间增加;若为匀减速运动,速度和位移都随时间减小
解析:根据v=v0+at和x=v0t+at2,知A、B选项不正确,由加速度公式知C正确.
当物体做匀减速运动时,速度减小但位移可以增大.
答案:C
3.汽车在平直公路上以10 m/s的速度做匀速直线运动,发现前面有情况而刹车,获得的加速度为2 m/s2.则
(1)汽车经过3 s时速度的大小为____________m/s;
(2)汽车经5 s时速度的大小是_______________;
(3)汽车经过10 s时速度的大小是______________.
解析:汽车刹车问题先要求出刹车过程的总时间,然后再讨论在不同时刻的运动情况.
由vt=v0+at可得,0=10-2t,t=5 s,即刹车时间为5 s.
汽车经3 s时速度大小v=v0+at=(10-2×3) m/s=4 m/s.
汽车经10 s时速度大小为0.
答案:(1)4 (2)0 (3)0
4.一质点做直线运动的x-t图象如图2-3-4所示,则质点在各段时间内做什么运动?
图2-3-4
解析:设质点从O点开始沿x轴运动,如图所示.在0—t1时间内,质点沿x轴正向做匀速直线运动,t1时刻到达A点;t1—t2时间内,x-t图象是一条平行于t轴的直线,位移没有变大也没有变小,即在这段时间内质点的位置未变,一直停在A点;在t2—t3时间内,x-t图象是一条倾斜的直线,质点做匀速直线运动,位移不断减小,说明质点由A点向O点运动,t3时刻到达OA之间某点B.
答案:见解析
我综合 我发展
5.一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速直线运动,接着做匀减速直线运动,开到乙地刚好停止,其速度图象如图2-3-5所示.那么0—t0和t0—3t0两段时间内( )
图2-3-5
A.加速度大小之比为3∶1 B.位移大小之比为1∶2
C.平均速度大小之比为2∶1 D.平均速度大小之比为1∶1
解析:在v-t图象中,加速度的大小可以根据直线的斜率求得,而位移的大小可以根据图象和坐标轴所围的面积求得.平均速度可以根据v=x/t求得.
可得:0—t0和t0—3t0两段时间内,加速度大小之比为2∶1,位移大小之比为1∶2,平均速度大小之比为1∶1.
答案:BD
6.两辆完全相同的汽车,沿平直路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住后,后车以前车刹车时的加速度开始刹车.已知前车在刹车过程中行驶的距离为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少为( )
A.s B.2s C.3s D.4s
解析:以前车为参考系,后车相当于先以初速度为0、加速度为a做匀加速直线运动,后以同样大小的加速度a做匀减速直线运动,而后通过的位移即两车匀速行驶的距离.因此s总=at2+at2.已知前车在刹车过程中行驶的距离为s,则at2=s,所以s总=2s.
答案:B
7.(2006广东高考A卷,2)a、b两物体从同一位置沿同一直线运动,它们的速度图象如图2-3-6所示,下列说法正确的是( )
图2-3-6
A.a、b加速时,物体a的加速度大于物体b的加速度
B.20秒时,a、b两物体相距最远
C.60秒时,物体a在物体b的前方
D.40秒时,a、b两物体速度相等,相距200 m
解析:v-t图象上直线的斜率反映加速度的大小,所以b的加速度大于a的加速度,A错;20秒时,a、b相距500 m,不是最远的,而是二者速度相等时相距最远,60秒时a的位移大于b的位移,所以a在b的前方,C对;40秒时,a、b速度相等,相距最远,相距500 m,所以D错.
答案:C
8.一辆巡逻车最快能在10 s内由静止加速到最高速度50 m/s,并能保持这个速度匀速行驶,问该巡逻车在平直的高速公路上由静止追上前方2 000 m处正以35 m/s的速度匀速行驶的汽车,至少需要多长时间?(巡逻车加速过程,加速度恒定)
解析:巡逻车以最大加速度加速,以最高速度行驶时所用的时间最短,设追及所需最短时间为t,则在这段时间内汽车行驶了s1=v1t,巡逻车加速过程行驶了s2=t0
匀速行驶了s3=v2(t-t0),追及时:s2+s3=s0+s1,即
v0t0+v2(t-t0)=s0+v1t
所以t=150 s.
答案:150 s
我创新 我超越
9.有种理论认为百慕大三角区之谜是水合天然气引起的.在海底,由于温度低、压力大,动植物遗体腐烂变成天然气与水结合,形成了固态的水合天然气.这些水合天然气稳定的条件一旦受到破坏,就可分解出气态的天然气气泡上升,上升的气泡流导致海底的压力变小,更多的固态水合天然气汽化.这样导致大量天然气溢出海面.大量的天然气气泡使海水的密度变小,浮力下降,当船舶驶入这个区域时,海水浮力支撑不住船舶的重力,而使船舶沉入海底.飞机飞入这个地带,则可引燃天然气,而被烧毁坠入海中.
一艘水上排水量为900 t、水下排水量为1 200 t、最大潜水深度为250 m的潜水艇在该地区海面下100 m处巡航,突然海水密度骤降(假如潜艇所在处及它下面海水密度从1.03×103 kg/m3骤变为0.9×103 kg/m3),5 s后潜艇发现此情况并立即采取措施,以最快的速度排泄艇内贮水舱中的水,当它刚止住自己加速下坠时已在水面下200 m处,不计阻力.试分析:
(1)潜水艇在采取措施前的5 s内下坠了多大距离?这时它的速度是多少?
(2)假如潜水艇一直保持排水速度不变,它做什么运动?加速度大小如何变化?能否摆脱葬身海底的厄运?
答案:略
更上一层楼
基础·巩固·达标
1.如图2-3-9所示为甲、乙两物体的x-t图象,则( )
图2-3-9
A.甲、乙两物体都做匀速直线运动
B.若甲、乙两物体在同一直线上运动,则一定会相遇
C.t1时刻甲、乙相遇
D.t2时刻甲、乙相遇
解析:本题考查物体的x-t图象,由图象可知甲、乙两物体都做匀速直线运动,但甲的位移增大,而乙的位移不断减小,甲乙两物体的运动方向相反,但都做匀速直线运动。
答案:ABC
2.一辆汽车以10 m/s的速度沿平直公路匀速运动,司机发现前方有障碍物立即减速,以0.2 m/s2的加速度做匀减速运动,减速后一分钟内汽车的位移为( )
A.240 m B.250 C.260 m D.90 m
解析:当t=50 s时汽车停止运动,所以x=m=250 m。
答案:B
3.一质点沿Ot坐标轴运动,t=0时,位于坐标原点,图2-3-10为质点做直线运动的速度—时间图象。由图可知
图2-3-10
(1)该质点的位移随时间变化的关系式是x=______________;
(2)在时间t=_____________s时质点距坐标原点最远;
(3)从t=0到t=20 s内质点的位移是_____________,通过的路程是_____________。
解析:由图象可知v0=-4 m/s,斜率为0.4,则x=v0t+at2=-4t+0.2t2,物体10 s前沿负方向运动,10 s后返回,所以10 s时距原点最远。20 s时返回原点,位移为0,路程为40 m。
答案:(1)-4t+0.2t2 (2)10 (3)0 40 m
4.物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2 m,BC=3 m,CD=4 m,且物体通过AB、BC、CD所用的时间相等,则OA之间的距离为_________________m(如图2-3-11)。
图2-3-11
解析:本题考查位移公式、速度公式、位移速度关系式的综合应用。怎样选择公式去解题,是解答这类问题的关键。
设时间间隔为t,则vB=,所以a=,OA=OB-AB=-2 m=1.125 m。
答案:1.125
5.有一个做匀加速直线运动的质点,它在开始的两个连续相等的时间间隔内所通过的路程分别是24 m和64 m,每一时间间隔为4 s。则质点运动的初速度和加速度分别为___________m/s和__________m/s2。
解析:物体开始运动4 s后的瞬时速度v==(24+64)/8 m/s=11 m/s,所以x1=·t,即v0=-11 m/s=1 m/s,又因为x1=v0·t+at2,所以a=2.5 m/s2。
答案:1 2.5
6如图2-3-12所示,为一直升机垂直起飞过程的v-t图象,则直升机运动中有几个不同性质的过程,计算飞机能到达的最大的高度?25 s时飞机的高度是多少?
图2-3-12
解:由v-t图象的意义得0—5 s内匀加速,5—15 s内匀速;
15—20 s内匀减速;0—20 s内速度方向一直向上,
20—25 s内向下匀加速,速度是负值,
可知,当20 s时竖直向上的位移最大。位移的大小为图线与坐标轴围成的“面积”:
s=×40 m=600 m
当20 s到25 s阶段飞机向下运动:
s1= m=200 m
因此,25 s时飞机的高度为400 m。
7.火车沿平直铁轨匀加速前进,通过某一路标时的速度为10.8 km/h,1 min后变成 54 km/h,再经一段时间,火车的速度达到 64.8 km/h。求所述过程中,火车的位移是多少。
解:火车一直做匀加速运动,其位移可由多种不同方法求解。
解法1:整个过程的平均速度:=m=m/s
时间t=75 s,则火车位移:x==×75 m=787.5 m
解法2:由x=v0·t+at2得位移x=3×75+×0.2×52=787.5 m。
8.一块木板厚为d=10 mm,子弹垂直板面穿过木板,已知穿透前后子弹的速度分别为v1=50 m/s和v2=30 m/s,求穿透所用时间是多少。
解析:本题考查速度、位移关系的公式的掌握,注意在应用公式时,要选取正方向。
解:d==·t,即10×10-3 s=·t,解得t=2.5×10-4 s。
9.汽车做匀加速直线运动,由A到B和由B到C所用时间均是2 s,且前2 s和后2 s的位移分别为8 m、12 m,求汽车运动的加速度和初速度、末速度。
解析:本题考查速度公式、位移公式的综合应用,在解答题目的过程中,要注意灵活选用适当的公式,尽量使解题过程简单些。
解:vB==m/s=5 m/s,xAB=·t,
vA=3 m/s,xBC=·t,所以vC=7 m/s,a==1 m/s2。
10.汽车以54 km/h的速度在水平路面上运动,紧急刹车后,以7.5 m/s2的加速度做匀减速直线运动。求汽车刹车后3 s内车的位移。
解:54 km/h=15 m/s,当汽车以v0=15 m/s的初速度、7.5 m/s2的加速度匀减速行驶时,根据速度公式:vt=v0+at得t==2 s,经过2 s汽车就停止运动,所以汽车刹车后3 s内的位移与2 s内的位移是相等的,位移大小为x=v0t+at2=15 m/s×2 s-×7.5 m/s2×(2 s)2=15 m,或者根据公式:v02=2ax得x=m=15 m。
综合·应用·创新
11.两辆完全相同的汽车,沿平直路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住后,后车以前车刹车时的加速度开始刹车。已知前车在刹车过程中行驶的距离为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少为( )
A.s B.2s C.3s D.4s
解析:以前车为参考系,后车相当于先以初速度为0,加速度为a做匀加速直线运动,后以同样大小的加速度a做匀减速直线运动,而后撤通过的位移即两车匀速行驶时距离。因此 s总=at2+at2。已知前车在刹车过程中行驶的距离为s,则at2=s,所以 s总=2s。
答案:B
12.据国外报道,科学家正在研制一种可以发射小型人造卫星的超级大炮。它能够将一个体积约为2 m3(底面面积约为0.8 m2)、质量为400 kg的人造卫星从大炮中以300 m/s的速度发射出去,再加上辅助火箭的推进,最终将卫星送入轨道。发射部分有长650 m左右的加速管道,内部分隔成许多气室,当卫星每进入一个气室,该气室的甲烷、空气混合气体便点燃产生推力,推动卫星加速,其加速度可以看作是恒定的。则这种大炮的加速度的大小约为____________m/s2。
解析:人造卫星在大炮中的初速度v0=0,末速度为v1=300 m/s,加速的位移为s=650 m,由公式vt2=2as,得a=m/s2=69.2 m/s2。
答案:69.2
13.质点由静止开始以1.2 m/s2的加速度做匀加速直线运动,经过10 s后,改做匀速直线运动,又经5 s,接着做匀减速直线运动,再经过20 s停止。求:
(1)质点做匀速直线运动的速度大小和匀减速直线运动的加速度;
(2)整个过程中运动的位移大小。
解:(1)加速10 s运动的位移x1=1/2a1t12=60 m。
10 s末的速度v1=a1t1=12 m/s
匀速运动的位移x2=v1t2=60 m
减速过程中0=v1+a2t3,a2=-0.6 m/s2,x3=120 m。
(2)x=x1+x2+x3=240 m。
14.一辆巡逻车最快能在10 s内由静止加速到最高速度50 m/s,并能保持这个速度匀速行驶,问该巡逻车在平直的高速公路上由静止追上前方2 000 m处正以35 m/s的速度匀速行驶的汽车,至少需要多长时间?(巡逻车加速过程,加速度恒定)
解:巡逻车以最大加速度加速,以最高速度行驶时所用的时间最短,设追及所需最短时间为t,则在这段时间内汽车行驶了 s1=v1t。巡逻车加速过程行驶了 s2=。
匀速行驶了 s3=v2(t-t0),追及时: s2+ s3= s0+ s1。即
()v0t0+v2(t-t0)= s0+v1t
所以t=150 s。
15.如图2-3-13所示,在国庆阅兵式中,某直升机在地面上空某高度A处静止待命,要求该机10 h 56 min 40 s从静止状态沿水平方向做匀加速直线运动,经过AB段加速后,进入BC段的匀速受阅区,11时准时通过C位置,已知sAB=5 km,sBC=10 km。问:
图2-3-13
(1)直升机在BC段的速度为多大
(2)在AB段做匀加速运动的加速度为多大
解:(1)由题意知,飞机由A到B为匀加速直线运动,由B到C为匀速直线运动,共用时间3 min 20 s,即t=200 s。设匀速运动时的速度为v,AB段所用时间为t1,BC段所用时间为t2,则vt1=sAB=5 000 m, vt2=sBC=10 000 m,t1+t2=200 s,几个公式联立得v=100 m/s。
t1=t2=100 s。
(2)设AB段匀加速的加速度为a,则v=at1,a=1=1 m/s2。
16.在高速公路上,有时会发生“追尾”的事故——后面的汽车撞上前面的汽车。请分析一下,造成“追尾”事故的原因有哪些 我国高速公路的最高车速限制为120 km/h。设某人驾车正以最高时速沿平直高速公路行驶,该车刹车时产生的加速度大小为5 m/s2,司机的反应时间(从意识到应该停车至操作刹车的时间)为0.6—0.7 s。请分析一下,应该如何计算行驶时的安全车距
解析:从后车的运动考虑,造成“追尾”的原因主要有以下几方面:(1)车速过快;(2)跟前车的车距过小;(3)司机的反应较迟缓;(4)车的制动性能较差。
解:当司机发现紧急情况(如前方车辆突然停下)后,在反应时间内,汽车仍以原来的速度做匀速直线运动;刹车后,汽车匀减速滑行。所以,刹车过程中汽车先后做着两种不同的运动,行驶时的安全车距应等于两部分位移之和。其运动情况如上图所示。为确保安全行车,反应时间应取0.7 s计算。
汽车原来的速度v0=120 km/h=33.3 m/s。在反应时间t1=0.7 s内,汽车做匀速直线运动的位移为 s1=v0t1=33.3×0.7 m=23.3 m。刹车后,汽车做匀减速运动,滑行时间为t2=s=6.7 s,汽车刹车后滑行的位移为 s2=v0t+at2=110.9 m,所以行驶时
的安全车距应为 s= s1+ s2=23.3 m+110.9 m=134.2 m。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
