沪科版数学七年级下册 8.1 幂的运算(第2课时)课件(共17张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.1 幂的运算(第2课时)课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 395.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 09:52:20 | ||
图片预览






文档简介
(共17张PPT)
第8章 整式乘法与因式分解
8.1 幂的运算
(第2课时)
情境导入
火星有两颗卫星,即火卫1和火卫2,火卫1的质量约为1016千克。截止到2005年4月,已发现木星有58颗卫星,其中木卫4的质量约为1023千克,木卫4的质量约为火卫1质量的多少倍?
思考:木卫4的质量约为火卫1质量的多少倍?
1023÷1016=?
根据同底数幂的乘法法则进行计算:
28×27= 52×53=
a2×a5= 3m-n×3n=
215
55
a7
3m
( )× 27=215
( )×53= 55
( )×a5=a7
( )×3n =
28
a2
52
乘法与除法互为逆运算
215÷27=( )
=215-7
55÷53=( )
=55-3
a7÷a5=( )
=a7-5
3m÷3m-n=( )
=3m-(m-n)
28
52
a2
3n
填一填:
上述运算你发现了什么规律吗?
3m-n
3m
新知探究1
推导过程:
幂的运算性质4:
同底数幂相除,底数不变,指数相减.
—— 同底数幂的除法运算法则
同底数幂的除法运算法则的符号表示:
am · an
=
am-n
(a≠0,m,n都是正整数,且m>n)
注意:因为0不能作除数,所以a≠0.
例1 计算:
(1)x8÷x2 ;
(2) a4 ÷a ;
(3)(ab) 5÷(ab)2;
解: (1) x8 ÷x2=x 8-2=x6.
(2)a4 ÷a =a 4-1=a3.
(3) (ab) 5÷(ab)2=(ab)5-2=(ab)3=a3b3.
例题讲解
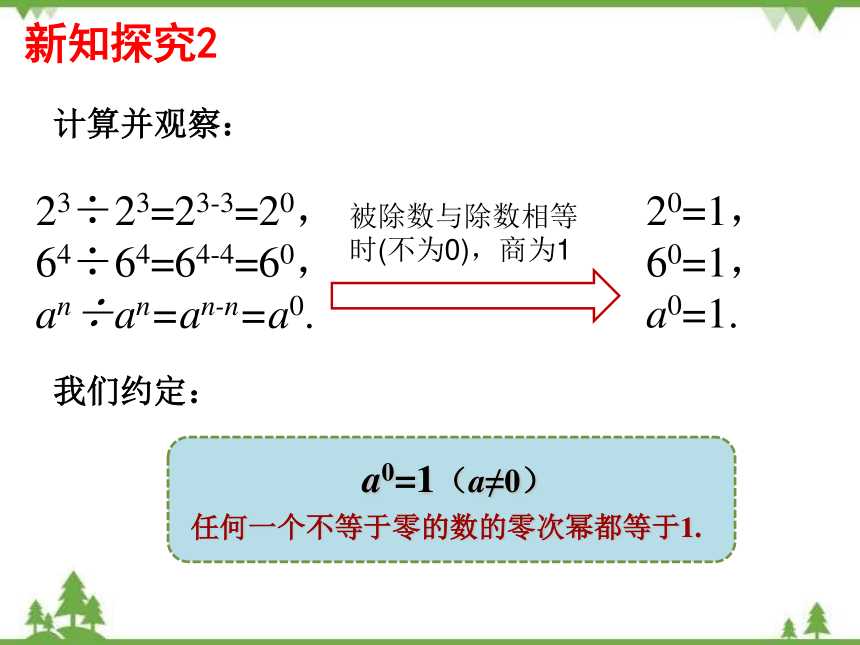
新知探究2
计算并观察:
23÷23=23-3=20,
64÷64=64-4=60,
an÷an=an-n=a0.
20=1,
60=1,
a0=1.
被除数与除数相等时(不为0),商为1
我们约定:
a0=1(a≠0)
任何一个不等于零的数的零次幂都等于1.
例2 用小数或分数表示下列各数:
(1)10-3; (2)70×8-2; (3)1.6×10-4.
解:
(1)10-3
=0.001.
(2)70×8-2
(3)1.6×10-4
=1.6×0.0001
=0.00016.
例题讲解
例如,864000可以写成 .
绝对值大于10的数记成a×10n的形式,其中1≤|a|<10,n是正整数.
怎样把0.0000864用科学记数法表示?
8.64×105
思考:
问题:怎样用科学记数法表示较大的数?
新知探究3
0.000 001= =10-6,
-0.000 22= = -2.2×10-4.
观察并归纳:
绝对值小于1的数可记成±a×10-n的形式,即科学记数法.
用科学记数法表示绝对值小于1的数:
记成±a×10 -n的形式,其中1≤a<10 ,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),这种记数方法是科学记数法.
归纳对比:
科学记数法 表示绝对值小于1的数:a×10-n 表示绝对值大于1的数:a×10n
a 1≤∣a∣<10 1≤∣a∣<10
n n是正整数,n是这个数左起第一个不是0的数字前面所有零的个数 n是正整数,n等于原数的整数位数减1
例3(1)用小数表示:3.6×10-3.
(2)用科学记数法表示下列各数.
①0.001; ②-0.0000896;
解:(1)
(2)①0.001=1×10-3;
②-0.0000896=-8.96×10-5;
例题讲解
随堂练习
2.计算(结果用整数或分数表示):
1
1
64
3.用科学记数法表示下列各数:(1)0.0000001; (2)0.0000004176.
解:(1)0.0000001=1×10-7;
(2)0.0000004176=4.176×10-7.
1.同底数幂的除法运算法则的符号表示:
am · an=
am-n
(a≠0,m,n都是正整数,且m>n)
课堂小结
a0=1(a≠0)
任何一个不等于零的数的零次幂都等于1.
2.零次幂:
记成±a×10 - n的形式,其中1≤a<10 ,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),这种记数方法是科学记数法.
4.用科学记数法表示绝对值小于1的数:
a-p= (a≠0, p是正整数)
任何一个不等于零的数 - p(p是正整数)次幂,等于这个数的p次幂的倒数.
3.负整数指数幂:
第8章 整式乘法与因式分解
8.1 幂的运算
(第2课时)
情境导入
火星有两颗卫星,即火卫1和火卫2,火卫1的质量约为1016千克。截止到2005年4月,已发现木星有58颗卫星,其中木卫4的质量约为1023千克,木卫4的质量约为火卫1质量的多少倍?
思考:木卫4的质量约为火卫1质量的多少倍?
1023÷1016=?
根据同底数幂的乘法法则进行计算:
28×27= 52×53=
a2×a5= 3m-n×3n=
215
55
a7
3m
( )× 27=215
( )×53= 55
( )×a5=a7
( )×3n =
28
a2
52
乘法与除法互为逆运算
215÷27=( )
=215-7
55÷53=( )
=55-3
a7÷a5=( )
=a7-5
3m÷3m-n=( )
=3m-(m-n)
28
52
a2
3n
填一填:
上述运算你发现了什么规律吗?
3m-n
3m
新知探究1
推导过程:
幂的运算性质4:
同底数幂相除,底数不变,指数相减.
—— 同底数幂的除法运算法则
同底数幂的除法运算法则的符号表示:
am · an
=
am-n
(a≠0,m,n都是正整数,且m>n)
注意:因为0不能作除数,所以a≠0.
例1 计算:
(1)x8÷x2 ;
(2) a4 ÷a ;
(3)(ab) 5÷(ab)2;
解: (1) x8 ÷x2=x 8-2=x6.
(2)a4 ÷a =a 4-1=a3.
(3) (ab) 5÷(ab)2=(ab)5-2=(ab)3=a3b3.
例题讲解
新知探究2
计算并观察:
23÷23=23-3=20,
64÷64=64-4=60,
an÷an=an-n=a0.
20=1,
60=1,
a0=1.
被除数与除数相等时(不为0),商为1
我们约定:
a0=1(a≠0)
任何一个不等于零的数的零次幂都等于1.
例2 用小数或分数表示下列各数:
(1)10-3; (2)70×8-2; (3)1.6×10-4.
解:
(1)10-3
=0.001.
(2)70×8-2
(3)1.6×10-4
=1.6×0.0001
=0.00016.
例题讲解
例如,864000可以写成 .
绝对值大于10的数记成a×10n的形式,其中1≤|a|<10,n是正整数.
怎样把0.0000864用科学记数法表示?
8.64×105
思考:
问题:怎样用科学记数法表示较大的数?
新知探究3
0.000 001= =10-6,
-0.000 22= = -2.2×10-4.
观察并归纳:
绝对值小于1的数可记成±a×10-n的形式,即科学记数法.
用科学记数法表示绝对值小于1的数:
记成±a×10 -n的形式,其中1≤a<10 ,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),这种记数方法是科学记数法.
归纳对比:
科学记数法 表示绝对值小于1的数:a×10-n 表示绝对值大于1的数:a×10n
a 1≤∣a∣<10 1≤∣a∣<10
n n是正整数,n是这个数左起第一个不是0的数字前面所有零的个数 n是正整数,n等于原数的整数位数减1
例3(1)用小数表示:3.6×10-3.
(2)用科学记数法表示下列各数.
①0.001; ②-0.0000896;
解:(1)
(2)①0.001=1×10-3;
②-0.0000896=-8.96×10-5;
例题讲解
随堂练习
2.计算(结果用整数或分数表示):
1
1
64
3.用科学记数法表示下列各数:(1)0.0000001; (2)0.0000004176.
解:(1)0.0000001=1×10-7;
(2)0.0000004176=4.176×10-7.
1.同底数幂的除法运算法则的符号表示:
am · an=
am-n
(a≠0,m,n都是正整数,且m>n)
课堂小结
a0=1(a≠0)
任何一个不等于零的数的零次幂都等于1.
2.零次幂:
记成±a×10 - n的形式,其中1≤a<10 ,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),这种记数方法是科学记数法.
4.用科学记数法表示绝对值小于1的数:
a-p= (a≠0, p是正整数)
任何一个不等于零的数 - p(p是正整数)次幂,等于这个数的p次幂的倒数.
3.负整数指数幂:
