19.2.1矩形 学案
图片预览

文档简介
学科:数学 年级:八年级 主备人: 审核人:
课题:矩形(一) 课型:预习+展示 小主人姓名:
*学习目标*:1、掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系;
2、从边、角、对角线方面,让学生观察或度量猜想矩形的特殊性质,会初步运用矩形的概念和性质来解决有关问题.
*学习重点*: 矩形的性质.
*学习难点*:矩形的性质的灵活应用.
学习过程
学法指导
一。*知识回顾*
平行四边形的性质___________________
____________________
平行四边形的判定方法_______________
_______________
_______________
二.*能力生成*
活动一 1、 ①平行四边形活动框架在变化过程中,哪些量发生了变化?哪些量没有变化?从中得到哪些结论?你能试着说明结论是否成立?
1.矩形的定义:有一个角是直角的平行四边形,叫做矩形。由此可见,矩形是特殊的 ,它具有平行四边形的所有性质。
2.结合上面图形说说矩形有哪些平行四边形不具有的特殊性质?
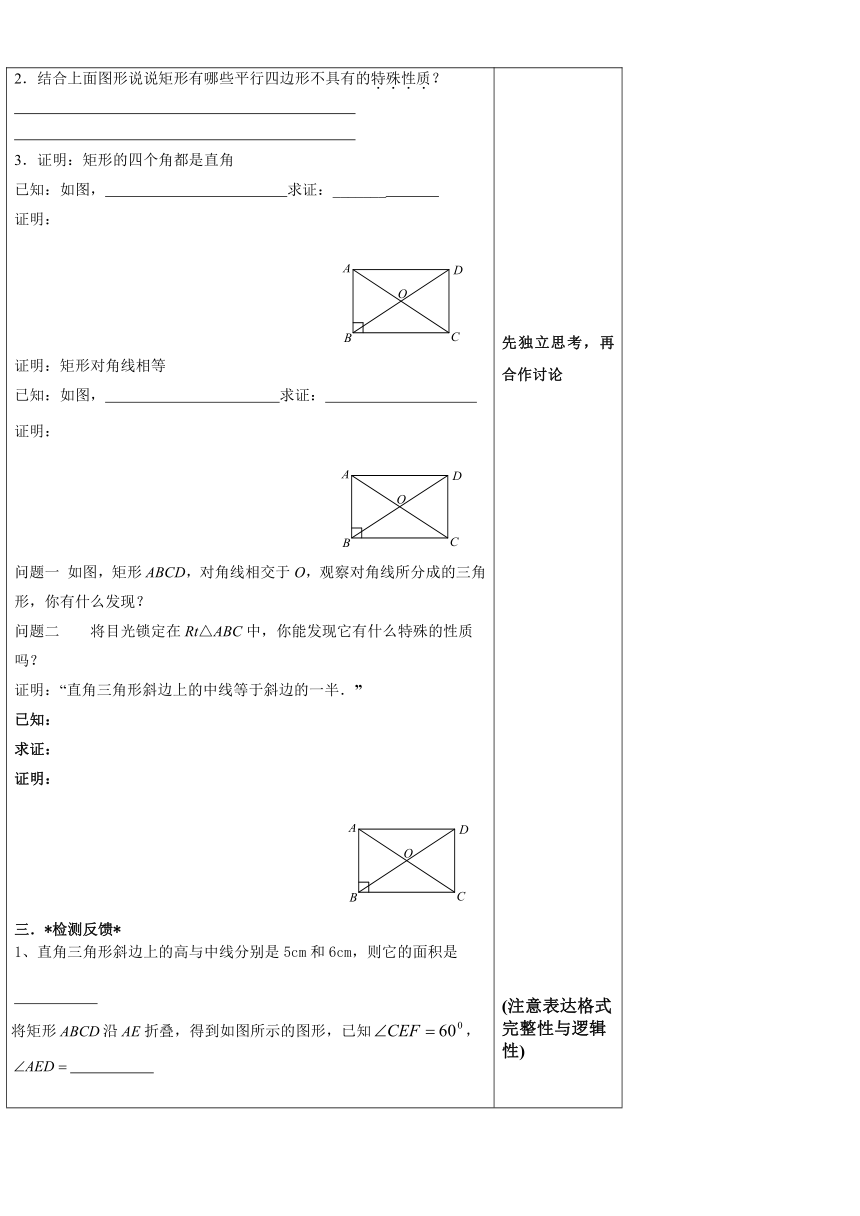
3.证明:矩形的四个角都是直角
已知:如图, 求证:_______
证明:
证明:矩形对角线相等
已知:如图, 求证:
证明:
问题一 如图,矩形ABCD,对角线相交于O,观察对角线所分成的三角形,你有什么发现?
问题二 将目光锁定在Rt△ABC中,你能发现它有什么特殊的性质吗?
证明:“直角三角形斜边上的中线等于斜边的一半.”
已知:
求证:
证明:
三.*检测反馈*
1、直角三角形斜边上的高与中线分别是5cm和6cm,则它的面积是
将矩形沿折叠,得到如图所示的图形,已知,
2、已知:如图,矩形ABCD的两条对角线相交于点O,且AB=3, ,则AC= ,BC=
3、已知:如图,E为矩形ABCD内一点,且EB=EC。求证:EA=ED.
4、已知:矩形ABCD中,E是BC上 一点,于F,若 。
求证:CE=EF。
四.*拓展迁移*
1.已知矩形ABCD中,对角线交于点O,AB=6cm,BC=8cm,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值是多少?这个值会随点P的移动(不与A、D重合)而改变吗?请说明理由.
先独立思考,再合作讨论
(注意表达格式完整性与逻辑性)
即学即练
一分耕耘一分收获,你的收获有多大!
课题:矩形(一) 课型:预习+展示 小主人姓名:
*学习目标*:1、掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系;
2、从边、角、对角线方面,让学生观察或度量猜想矩形的特殊性质,会初步运用矩形的概念和性质来解决有关问题.
*学习重点*: 矩形的性质.
*学习难点*:矩形的性质的灵活应用.
学习过程
学法指导
一。*知识回顾*
平行四边形的性质___________________
____________________
平行四边形的判定方法_______________
_______________
_______________
二.*能力生成*
活动一 1、 ①平行四边形活动框架在变化过程中,哪些量发生了变化?哪些量没有变化?从中得到哪些结论?你能试着说明结论是否成立?
1.矩形的定义:有一个角是直角的平行四边形,叫做矩形。由此可见,矩形是特殊的 ,它具有平行四边形的所有性质。
2.结合上面图形说说矩形有哪些平行四边形不具有的特殊性质?
3.证明:矩形的四个角都是直角
已知:如图, 求证:_______
证明:
证明:矩形对角线相等
已知:如图, 求证:
证明:
问题一 如图,矩形ABCD,对角线相交于O,观察对角线所分成的三角形,你有什么发现?
问题二 将目光锁定在Rt△ABC中,你能发现它有什么特殊的性质吗?
证明:“直角三角形斜边上的中线等于斜边的一半.”
已知:
求证:
证明:
三.*检测反馈*
1、直角三角形斜边上的高与中线分别是5cm和6cm,则它的面积是
将矩形沿折叠,得到如图所示的图形,已知,
2、已知:如图,矩形ABCD的两条对角线相交于点O,且AB=3, ,则AC= ,BC=
3、已知:如图,E为矩形ABCD内一点,且EB=EC。求证:EA=ED.
4、已知:矩形ABCD中,E是BC上 一点,于F,若 。
求证:CE=EF。
四.*拓展迁移*
1.已知矩形ABCD中,对角线交于点O,AB=6cm,BC=8cm,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值是多少?这个值会随点P的移动(不与A、D重合)而改变吗?请说明理由.
先独立思考,再合作讨论
(注意表达格式完整性与逻辑性)
即学即练
一分耕耘一分收获,你的收获有多大!
