北京课改版数学八年级下册同步课时练习:第十五章 四边形 复习小结(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:第十五章 四边形 复习小结(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 166.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
复习小结
类型之一 多边形的内角和与外角和
1.(2021西城区一模)如果一个多边形的内角和是720°,那么这个多边形的边数是 ( )
A.8 B.7 C.6 D.5
2.(2021大兴区一模)若正多边形的一个内角是120°,则这个正多边形的边数为 ( )
A.6 B.5 C.4 D.3
3.(2021房山区一模)若一个多边形的每个外角都是72°,则该多边形的边数为 ( )
A.3 B.4 C.5 D.6
类型之二 平行四边形的性质与判定
4.如 ABCD的对角线AC,BD的交点为O,AC⊥AB,CD边的中点为E.若OA=2,AB=3,则OE= .
5.如在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.
(1)求证:四边形DBCF是平行四边形;
(2)若∠A=30°,BC=4,CF=6,求CD的长.
类型之三 特殊平行四边形的性质与判定
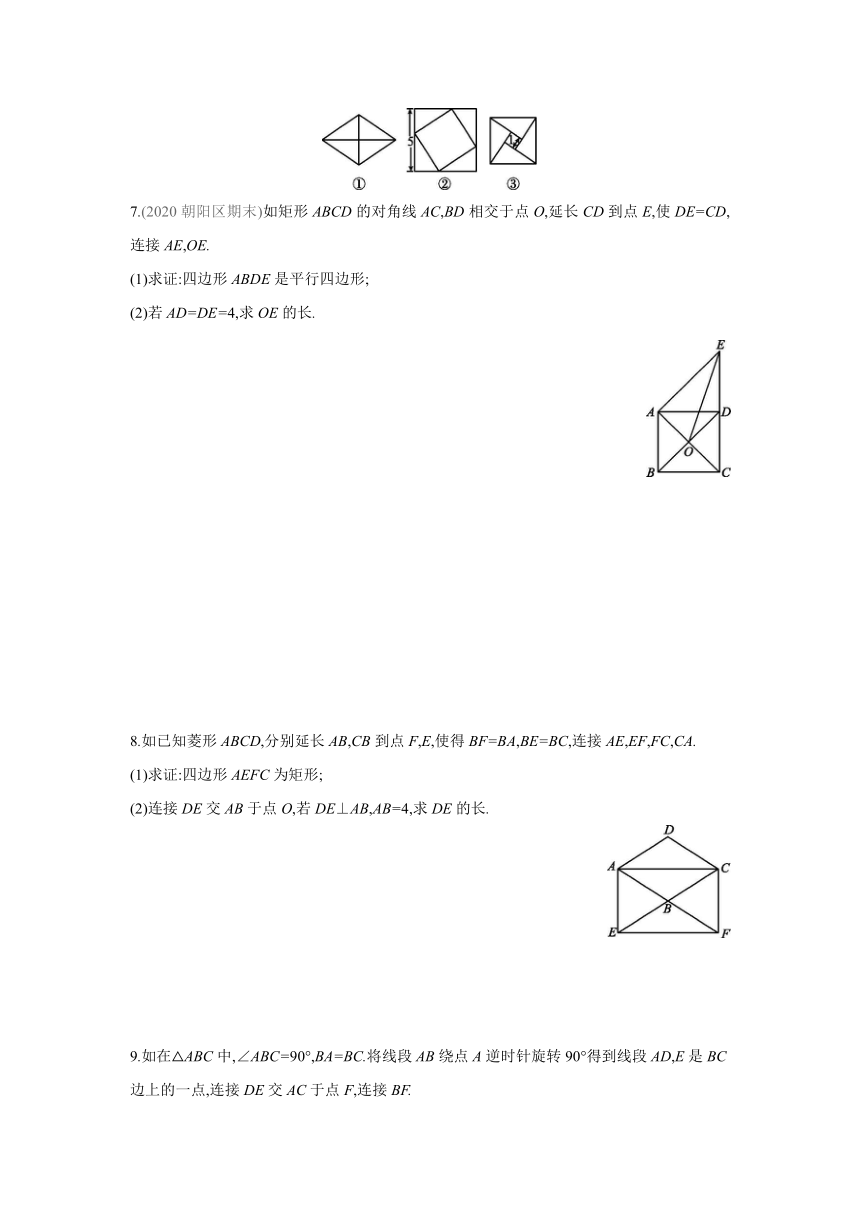
6.(2019北京)把中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如②③所示的正方形,则①中菱形的面积为 .
7.(2020朝阳区期末)如矩形ABCD的对角线AC,BD相交于点O,延长CD到点E,使DE=CD,连接AE,OE.
(1)求证:四边形ABDE是平行四边形;
(2)若AD=DE=4,求OE的长.
8.如已知菱形ABCD,分别延长AB,CB到点F,E,使得BF=BA,BE=BC,连接AE,EF,FC,CA.
(1)求证:四边形AEFC为矩形;
(2)连接DE交AB于点O,若DE⊥AB,AB=4,求DE的长.
9.如在△ABC中,∠ABC=90°,BA=BC.将线段AB绕点A逆时针旋转90°得到线段AD,E是BC边上的一点,连接DE交AC于点F,连接BF.
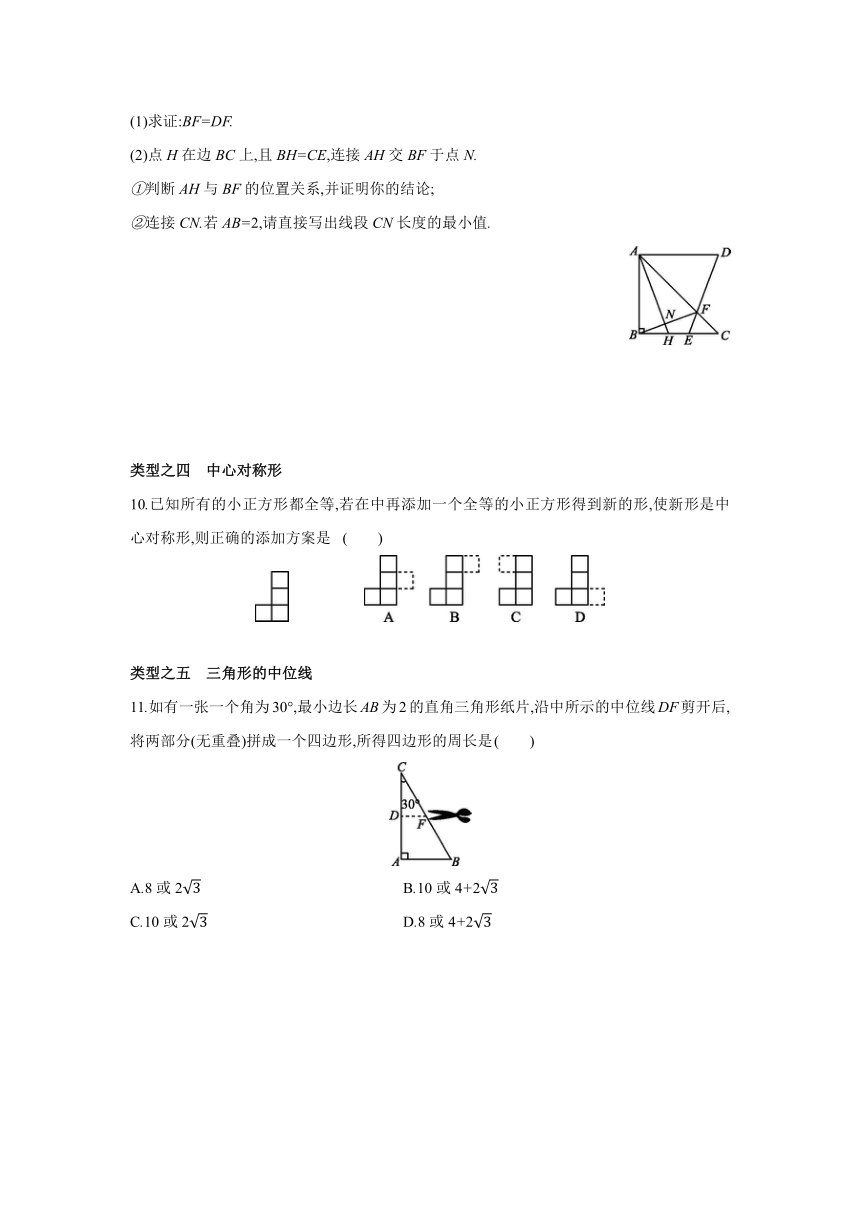
(1)求证:BF=DF.
(2)点H在边BC上,且BH=CE,连接AH交BF于点N.
①判断AH与BF的位置关系,并证明你的结论;
②连接CN.若AB=2,请直接写出线段CN长度的最小值.
类型之四 中心对称形
10.已知所有的小正方形都全等,若在中再添加一个全等的小正方形得到新的形,使新形是中心对称形,则正确的添加方案是 ( )
类型之五 三角形的中位线
11.如有一张一个角为30°,最小边长AB为2的直角三角形纸片,沿中所示的中位线DF剪开后,将两部分(无重叠)拼成一个四边形,所得四边形的周长是 ( )
A.8或2 B.10或4+2
C.10或2 D.8或4+2
详 解
1.C 2.A 3.C
4.2.5 解: ∵四边形ABCD是平行四边形,OA=2,
∴AC=2OA=4.
∵AC⊥AB,AB=3,∴BC=5.
∵CD边的中点为E, ABCD的对角线AC,BD的交点为O,
∴OE=BC=2.5.
5.解:(1)证明:∵E为CD的中点,∴CE=DE.
又∵EF=BE,∴四边形DBCF是平行四边形.
(2)∵四边形DBCF是平行四边形,
∴CF∥AB,DF∥BC,
∴∠FCG=∠A=30°,∠CGF=∠ACB=90°.
在Rt△FCG中,CF=6,∴FG=CF=3,
∴CG=3.
∵DF=BC=4,∴DG=1.
在Rt△DCG中,CD==2.
6.12 解: 如所示.
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
设OA=x,OB=y.由题意得
解得
∴AC=2OA=6,BD=2OB=4,
∴菱形ABCD的面积=AC·BD=×6×4=12.
7.解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
又∵DE=CD,
∴DE=AB,∴四边形ABDE是平行四边形.
(2)∵AD=DE=4,∠ADE=90°,
∴AE=4,∠EAD=45°.
∵四边形ABDE为平行四边形,
∴BD=AE=4.
在Rt△BAD中,O为BD的中点,
∴AO=BD=2.
∵AD=DE,DE=CD,∴AD=CD,
∴矩形ABCD是正方形,
则∠OAD=45°,
∴∠EAO=∠OAD+∠EAD=45°+45°=90°,
∴OE===2.
8.解:(1)证明:∵BF=BA,BE=BC,
∴四边形AEFC为平行四边形.
∵四边形ABCD为菱形,
∴BA=BC,∴BE=BF,
∴BA+BF=BC+BE,即AF=EC,
∴四边形AEFC为矩形.
(2)如,连接DE交AB于点O,连接DB.
∵四边形ABCD为菱形,BC=BE,
∴AD∥EB,且AD=BC=EB,
∴四边形AEBD为平行四边形.
∵DE⊥AB,∴四边形AEBD为菱形,
∴AE=AD,AB=2AO,ED=2EO.
在菱形ABCD中,AD=AB,AB=4,
∴AO=2,AE=4,
∴在Rt△AEO中,EO=2,∴DE=4.
9.解:(1)证明:∵BA=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°.
∵线段AB绕点A逆时针旋转90°得到线段AD,
∴∠BAD=90°,BA=DA,
∴∠FAD=∠FAB=45°.
又∵AF=AF,
∴△FAD≌△FAB,
∴BF=DF.
(2)①AH⊥BF.
证明:如(a),连接CD.
∵∠ABC+∠BAD=180°,
∴AD∥BC.
∵AD=AB=BC,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴四边形ABCD是矩形.
∵AB=BC,
∴四边形ABCD是正方形,
∴BA=CD,∠ABH=∠DCE.
又∵BH=CE,
∴△ABH≌△DCE,
∴∠BAH=∠CDE.
∵∠FCD=∠FCB=45°,CF=CF,CD=CB,
∴△CFD≌△CFB,
∴∠CDF=∠CBF,
∴∠BAH=∠CBF.
∵∠CBF+∠ABF=90°,
∴∠BAH+∠ABF=90°,
∴∠ANB=90°,
∴AH⊥BF.
②如(b),连接CN,取AB的中点O,连接ON,OC.
∵∠ANB=90°,AO=OB,∴ON=AB=1.
在Rt△OBC中,OC==.
∵CN≥OC-ON,∴CN≥-1,
∴CN的最小值为-1.
10.B
11.D 解: 由题意可得AB=2.
∵∠C=30°,∠A=90°,
∴BC=4,AC=2.
∵DF为△ABC的中位线,
∴CD=AD=,CF=BF=2,DF=1.
如①所示,可以拼成一个矩形,其周长为1+1+2++=4+2;
如②所示,可以拼成一个平行四边形,其周长为2+2+2+2=8;
如③所示,可以拼成一个等腰梯形,其周长为1+1+2+2+2=8.
综上,所得四边形的周长是4+2或8.
类型之一 多边形的内角和与外角和
1.(2021西城区一模)如果一个多边形的内角和是720°,那么这个多边形的边数是 ( )
A.8 B.7 C.6 D.5
2.(2021大兴区一模)若正多边形的一个内角是120°,则这个正多边形的边数为 ( )
A.6 B.5 C.4 D.3
3.(2021房山区一模)若一个多边形的每个外角都是72°,则该多边形的边数为 ( )
A.3 B.4 C.5 D.6
类型之二 平行四边形的性质与判定
4.如 ABCD的对角线AC,BD的交点为O,AC⊥AB,CD边的中点为E.若OA=2,AB=3,则OE= .
5.如在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.
(1)求证:四边形DBCF是平行四边形;
(2)若∠A=30°,BC=4,CF=6,求CD的长.
类型之三 特殊平行四边形的性质与判定
6.(2019北京)把中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如②③所示的正方形,则①中菱形的面积为 .
7.(2020朝阳区期末)如矩形ABCD的对角线AC,BD相交于点O,延长CD到点E,使DE=CD,连接AE,OE.
(1)求证:四边形ABDE是平行四边形;
(2)若AD=DE=4,求OE的长.
8.如已知菱形ABCD,分别延长AB,CB到点F,E,使得BF=BA,BE=BC,连接AE,EF,FC,CA.
(1)求证:四边形AEFC为矩形;
(2)连接DE交AB于点O,若DE⊥AB,AB=4,求DE的长.
9.如在△ABC中,∠ABC=90°,BA=BC.将线段AB绕点A逆时针旋转90°得到线段AD,E是BC边上的一点,连接DE交AC于点F,连接BF.
(1)求证:BF=DF.
(2)点H在边BC上,且BH=CE,连接AH交BF于点N.
①判断AH与BF的位置关系,并证明你的结论;
②连接CN.若AB=2,请直接写出线段CN长度的最小值.
类型之四 中心对称形
10.已知所有的小正方形都全等,若在中再添加一个全等的小正方形得到新的形,使新形是中心对称形,则正确的添加方案是 ( )
类型之五 三角形的中位线
11.如有一张一个角为30°,最小边长AB为2的直角三角形纸片,沿中所示的中位线DF剪开后,将两部分(无重叠)拼成一个四边形,所得四边形的周长是 ( )
A.8或2 B.10或4+2
C.10或2 D.8或4+2
详 解
1.C 2.A 3.C
4.2.5 解: ∵四边形ABCD是平行四边形,OA=2,
∴AC=2OA=4.
∵AC⊥AB,AB=3,∴BC=5.
∵CD边的中点为E, ABCD的对角线AC,BD的交点为O,
∴OE=BC=2.5.
5.解:(1)证明:∵E为CD的中点,∴CE=DE.
又∵EF=BE,∴四边形DBCF是平行四边形.
(2)∵四边形DBCF是平行四边形,
∴CF∥AB,DF∥BC,
∴∠FCG=∠A=30°,∠CGF=∠ACB=90°.
在Rt△FCG中,CF=6,∴FG=CF=3,
∴CG=3.
∵DF=BC=4,∴DG=1.
在Rt△DCG中,CD==2.
6.12 解: 如所示.
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
设OA=x,OB=y.由题意得
解得
∴AC=2OA=6,BD=2OB=4,
∴菱形ABCD的面积=AC·BD=×6×4=12.
7.解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
又∵DE=CD,
∴DE=AB,∴四边形ABDE是平行四边形.
(2)∵AD=DE=4,∠ADE=90°,
∴AE=4,∠EAD=45°.
∵四边形ABDE为平行四边形,
∴BD=AE=4.
在Rt△BAD中,O为BD的中点,
∴AO=BD=2.
∵AD=DE,DE=CD,∴AD=CD,
∴矩形ABCD是正方形,
则∠OAD=45°,
∴∠EAO=∠OAD+∠EAD=45°+45°=90°,
∴OE===2.
8.解:(1)证明:∵BF=BA,BE=BC,
∴四边形AEFC为平行四边形.
∵四边形ABCD为菱形,
∴BA=BC,∴BE=BF,
∴BA+BF=BC+BE,即AF=EC,
∴四边形AEFC为矩形.
(2)如,连接DE交AB于点O,连接DB.
∵四边形ABCD为菱形,BC=BE,
∴AD∥EB,且AD=BC=EB,
∴四边形AEBD为平行四边形.
∵DE⊥AB,∴四边形AEBD为菱形,
∴AE=AD,AB=2AO,ED=2EO.
在菱形ABCD中,AD=AB,AB=4,
∴AO=2,AE=4,
∴在Rt△AEO中,EO=2,∴DE=4.
9.解:(1)证明:∵BA=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°.
∵线段AB绕点A逆时针旋转90°得到线段AD,
∴∠BAD=90°,BA=DA,
∴∠FAD=∠FAB=45°.
又∵AF=AF,
∴△FAD≌△FAB,
∴BF=DF.
(2)①AH⊥BF.
证明:如(a),连接CD.
∵∠ABC+∠BAD=180°,
∴AD∥BC.
∵AD=AB=BC,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴四边形ABCD是矩形.
∵AB=BC,
∴四边形ABCD是正方形,
∴BA=CD,∠ABH=∠DCE.
又∵BH=CE,
∴△ABH≌△DCE,
∴∠BAH=∠CDE.
∵∠FCD=∠FCB=45°,CF=CF,CD=CB,
∴△CFD≌△CFB,
∴∠CDF=∠CBF,
∴∠BAH=∠CBF.
∵∠CBF+∠ABF=90°,
∴∠BAH+∠ABF=90°,
∴∠ANB=90°,
∴AH⊥BF.
②如(b),连接CN,取AB的中点O,连接ON,OC.
∵∠ANB=90°,AO=OB,∴ON=AB=1.
在Rt△OBC中,OC==.
∵CN≥OC-ON,∴CN≥-1,
∴CN的最小值为-1.
10.B
11.D 解: 由题意可得AB=2.
∵∠C=30°,∠A=90°,
∴BC=4,AC=2.
∵DF为△ABC的中位线,
∴CD=AD=,CF=BF=2,DF=1.
如①所示,可以拼成一个矩形,其周长为1+1+2++=4+2;
如②所示,可以拼成一个平行四边形,其周长为2+2+2+2=8;
如③所示,可以拼成一个等腰梯形,其周长为1+1+2+2+2=8.
综上,所得四边形的周长是4+2或8.
同课章节目录
