北京课改版数学八年级下册同步课时练习:第十五章 四边形 单元测试(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:第十五章 四边形 单元测试(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 174.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 09:59:38 | ||
图片预览


文档简介
第十五章 四边形 单元测试
一、选择题(本题共7个小题,每小题4分,共28分)
1.在Rt△ABC中,CD是斜边AB上的中线,若AB=8,则CD的长是( )
A.6 B.5 C.4 D.3
2.若矩形对角线相交所成的钝角为120°,短边长为3.6 cm,则对角线的长为 ( )
A.3.6 cm B.7.2 cm C.1.8 cm D.14.4 cm
3.在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则对四边形ABCD的形状描述最准确的是 ( )
A.矩形 B.菱形 C.正方形 D.平行四边形
4.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是 ( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出② D.由①推出③,由③推出②
5.如在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,则∠DEC的度数为 ( )
A.78° B.75° C.60° D.45°
6.已知点A(0,0),B(0,4),C(3,t+4),D(3,t).记N(t)为 ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为 ( )
A.6,7 B.7,8 C.6,7,8 D.6,8,9
7.如在 ABCD中,AD=2AB,F是BC的中点,作AE⊥CD于点E,连接EF,AF,有下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF=S△AEF;④∠BFE=3∠CEF.其中一定成立的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本题共6个小题,每小题4分,共24分)
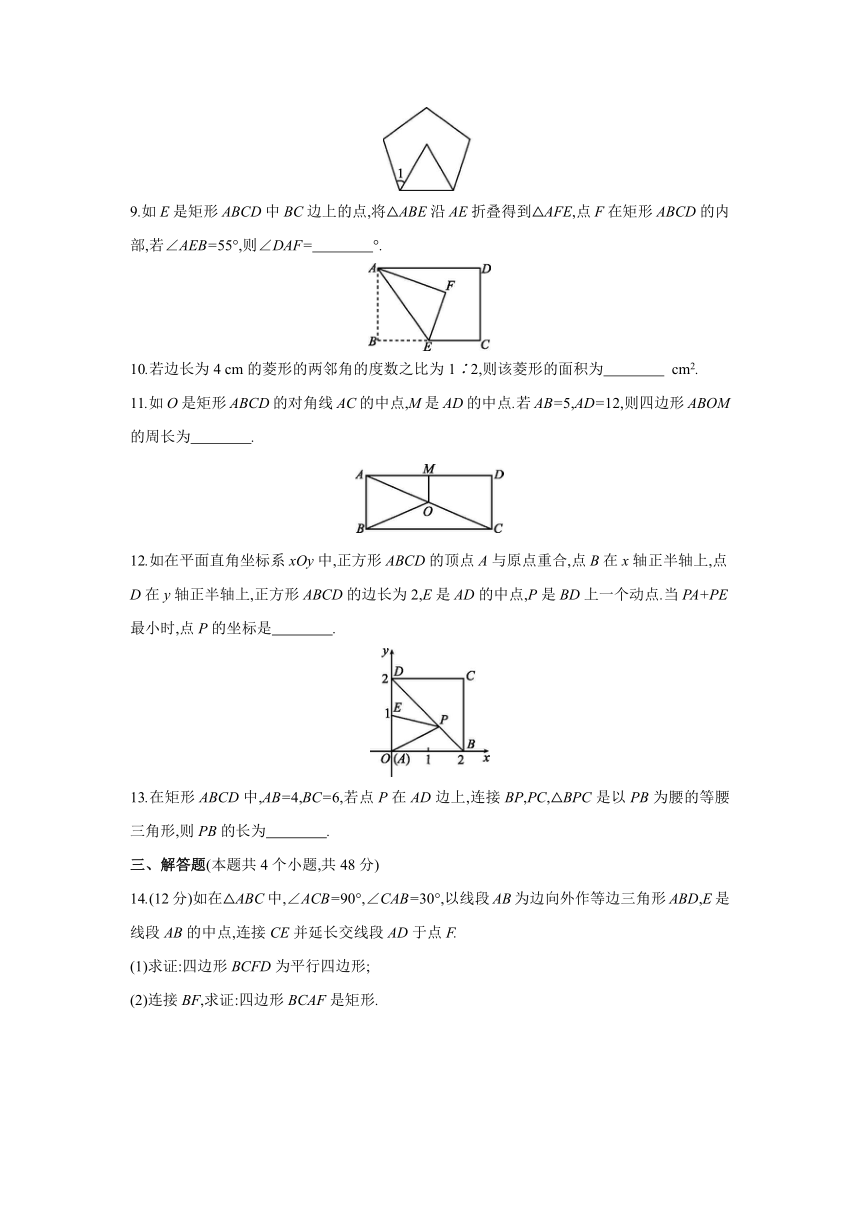
8.如在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1= °.
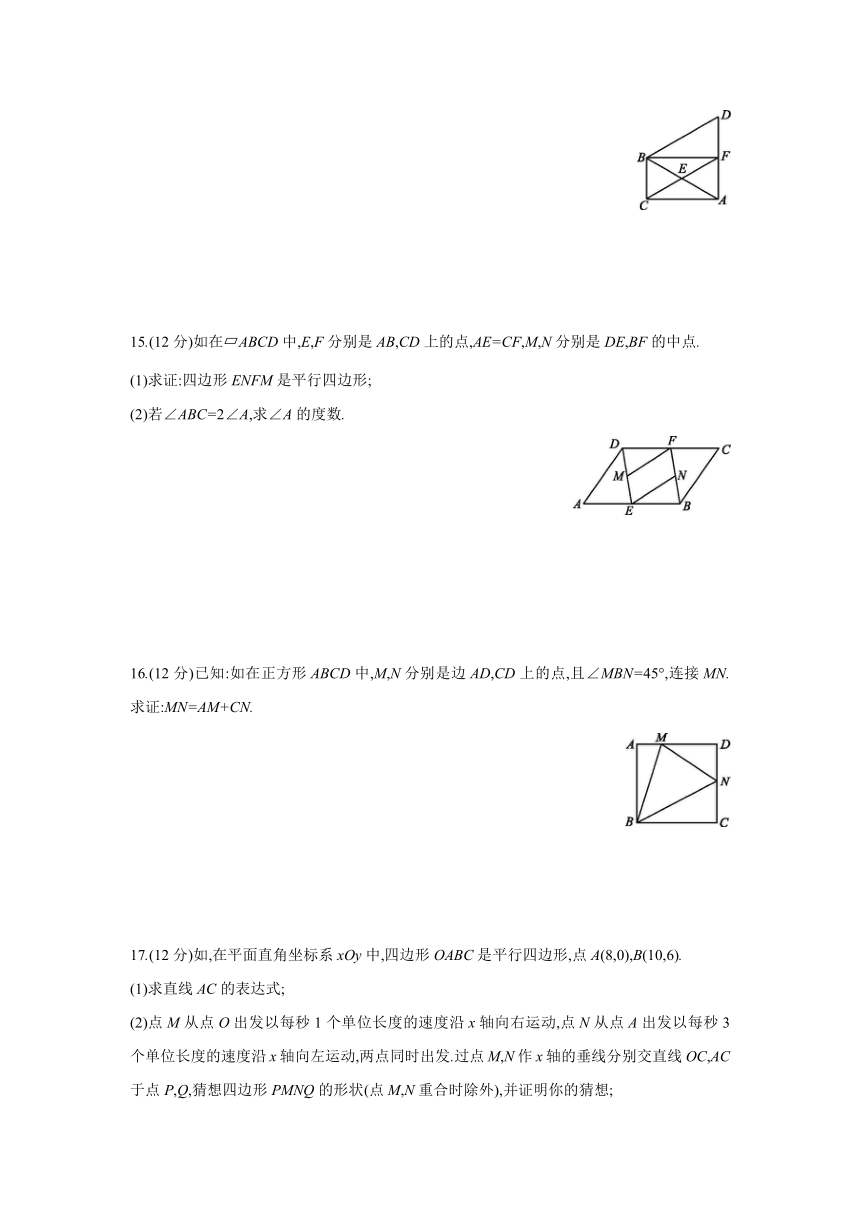
9.如E是矩形ABCD中BC边上的点,将△ABE沿AE折叠得到△AFE,点F在矩形ABCD的内部,若∠AEB=55°,则∠DAF= °.
10.若边长为4 cm的菱形的两邻角的度数之比为1∶2,则该菱形的面积为 cm2.
11.如O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
12.如在平面直角坐标系xOy中,正方形ABCD的顶点A与原点重合,点B在x轴正半轴上,点D在y轴正半轴上,正方形ABCD的边长为2,E是AD的中点,P是BD上一个动点.当PA+PE最小时,点P的坐标是 .
13.在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP,PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .
三、解答题(本题共4个小题,共48分)
14.(12分)如在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边三角形ABD,E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)连接BF,求证:四边形BCAF是矩形.
15.(12分)如在 ABCD中,E,F分别是AB,CD上的点,AE=CF,M,N分别是DE,BF的中点.
(1)求证:四边形ENFM是平行四边形;
(2)若∠ABC=2∠A,求∠A的度数.
16.(12分)已知:如在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN.求证:MN=AM+CN.
17.(12分)如,在平面直角坐标系xOy中,四边形OABC是平行四边形,点A(8,0),B(10,6).
(1)求直线AC的表达式;
(2)点M从点O出发以每秒1个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.过点M,N作x轴的垂线分别交直线OC,AC于点P,Q,猜想四边形PMNQ的形状(点M,N重合时除外),并证明你的猜想;
(3)在(2)的条件下,当点M运动 秒时,四边形PMNQ是正方形(直接写出结论).
详 解
1.C 2.B 3.B
4.A 解: 对角线相等的四边形推不出是正方形或矩形,故①→②,①→③错误,故选项B,C,D错误.故选A.
5.B 6.C
7.C 解: ①∵F是BC的中点,∴BF=FC.
在 ABCD中,AD=2AB,
∴BC=2AB=2CD,
∴BF=FC=AB,
∴∠AFB=∠BAF.
∵AD∥BC,
∴∠AFB=∠DAF,
∴∠BAF=∠FAD,
∴2∠BAF=∠BAD,故①正确;
②延长EF,交AB的延长线于点M.
∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠MBF=∠C.
∵F为BC的中点,∴BF=CF.
又∵∠BFM=∠CFE,
∴△MBF≌△ECF,∴FE=MF.
∵CE⊥AE,∴∠AEC=90°.
∴∠AEC=∠BAE=90°,
又∵FM=EF,∴EF=AF,故②正确;
③∵EF=FM,∴S△AEF=S△AFM.∵点B与点M不重合,∴S△ABF④设∠FEA=x,则∠FAE=x,
∴∠BAF=∠AFB=90°-x,∠EFA=180°-2x,
∴∠EFB=90°-x+180°-2x=270°-3x.
∵∠CEF=90°-x,
∴∠BFE=3∠CEF,故④正确.故选C.
8.48 解: 因为正五边形的一个内角为108°,正三角形的一个内角为60°,所以∠1=48°.
9.20 10.8 11.20
12., 解: 如,连接EC交BD于点P',连接OP'.
∵OP'=CP',∴P'O+P'E=P'C+P'E=CE,此时P'A+P'E的值最小,
∵B(2,0),D(0,2),
∴直线BD的表达式为y=-x+2.
∵E(0,1),C(2,2),
设直线EC的表达式为y=kx+b,则有解得
∴直线EC的表达式为y=x+1.
由解得∴P',.故答案为,.
13.5或6 解: 在矩形ABCD中,AB=CD=4,BC=AD=6.
如①,当PB=PC时,P是BC的垂直平分线与AD的交点,则AP=DP=AD=3.
在Rt△ABP中,由勾股定理,得PB===5;
如②,当BP=BC=6时,△BPC也是以PB为腰的等腰三角形.
综上所述,PB的长度是5或6.
故答案为5或6.
14.证明:(1)∵∠ACB=90°,∠CAB=30°,
∴BC=AB,∠ABC=60°.
∵△ABD是等边三角形,
∴∠ABD=∠BAD=60°,AB=AD,
∴∠ABC=∠BAD,
∴BC∥DA.
∵E是线段AB的中点,
∴CE=AB=BE=AE.
∵∠ABC=60°,
∴△BCE是等边三角形,
则∠BEC=60°=∠ABD,
∴BD∥CF,
∴四边形BCFD为平行四边形.
(2)∵BD∥CF,BE=AE,
∴AF=DF=AD.
又∵BC=DF,
∴BC=AF.
又∵BC∥DA,
∴四边形BCAF是平行四边形.
∵∠ACB=90°,
∴四边形BCAF是矩形.
15.解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
∵AE=CF,
∴BE=DF,
∴四边形DEBF为平行四边形,
∴DE=BF,DE∥BF.
又∵M,N分别是DE,BF的中点,
∴ME=FN,
∴四边形ENFM是平行四边形.
(2)∵四边形ABCD是平行四边形,
∴∠A+∠ABC=180°.
又∵∠ABC=2∠A,
∴3∠A=180°,
∴∠A=60°.
16.证明:如,延长DC到点E,使AM=CE,连接BE.
∵四边形 ABCD是正方形,
∴AB=CB,∠A=∠ABC=∠BCD=90°,
∴∠A=∠BCE=90°,
∴△ABM≌△CBE,
则∠1=∠2,BM=BE.
∵∠MBN=45°,
∴∠1+∠3=45°,
∴∠2+∠3=45°,
∴∠MBN=∠EBN.
又∵BN=BN,BM=BE,
∴△MBN≌△EBN,
∴MN=EN.
∵EN=CE+CN,
∴MN=CE+CN=AM+CN.
17.解:(1)∵四边形OABC是平行四边形,
点A(8,0),B(10,6),
∴C(2,6).
设直线AC的表达式为y=kx+b,
则解得
∴直线AC的表达式为y=-x+8.
(2)猜想:四边形PMNQ是矩形.
证明:如.
∵点C(2,6),
∴直线OC的表达式为y=3x.
设点M,N的运动时间为t秒,
则OM=t,AN=3t,
∴M(t,0),N(8-3t,0).
∵PM,QN垂直于x轴,点P,Q分别在直线OC,AC上,
∴P(t,3t),Q(8-3t,3t).
∴PM=QN=3t.
∵PM∥QN,
∴四边形PMNQ是平行四边形.
又PM⊥x轴,即PM⊥MN,
∴ PMNQ是矩形.
(3)或8
一、选择题(本题共7个小题,每小题4分,共28分)
1.在Rt△ABC中,CD是斜边AB上的中线,若AB=8,则CD的长是( )
A.6 B.5 C.4 D.3
2.若矩形对角线相交所成的钝角为120°,短边长为3.6 cm,则对角线的长为 ( )
A.3.6 cm B.7.2 cm C.1.8 cm D.14.4 cm
3.在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则对四边形ABCD的形状描述最准确的是 ( )
A.矩形 B.菱形 C.正方形 D.平行四边形
4.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是 ( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出② D.由①推出③,由③推出②
5.如在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,则∠DEC的度数为 ( )
A.78° B.75° C.60° D.45°
6.已知点A(0,0),B(0,4),C(3,t+4),D(3,t).记N(t)为 ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为 ( )
A.6,7 B.7,8 C.6,7,8 D.6,8,9
7.如在 ABCD中,AD=2AB,F是BC的中点,作AE⊥CD于点E,连接EF,AF,有下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF=S△AEF;④∠BFE=3∠CEF.其中一定成立的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本题共6个小题,每小题4分,共24分)
8.如在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1= °.
9.如E是矩形ABCD中BC边上的点,将△ABE沿AE折叠得到△AFE,点F在矩形ABCD的内部,若∠AEB=55°,则∠DAF= °.
10.若边长为4 cm的菱形的两邻角的度数之比为1∶2,则该菱形的面积为 cm2.
11.如O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
12.如在平面直角坐标系xOy中,正方形ABCD的顶点A与原点重合,点B在x轴正半轴上,点D在y轴正半轴上,正方形ABCD的边长为2,E是AD的中点,P是BD上一个动点.当PA+PE最小时,点P的坐标是 .
13.在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP,PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .
三、解答题(本题共4个小题,共48分)
14.(12分)如在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边三角形ABD,E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)连接BF,求证:四边形BCAF是矩形.
15.(12分)如在 ABCD中,E,F分别是AB,CD上的点,AE=CF,M,N分别是DE,BF的中点.
(1)求证:四边形ENFM是平行四边形;
(2)若∠ABC=2∠A,求∠A的度数.
16.(12分)已知:如在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN.求证:MN=AM+CN.
17.(12分)如,在平面直角坐标系xOy中,四边形OABC是平行四边形,点A(8,0),B(10,6).
(1)求直线AC的表达式;
(2)点M从点O出发以每秒1个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.过点M,N作x轴的垂线分别交直线OC,AC于点P,Q,猜想四边形PMNQ的形状(点M,N重合时除外),并证明你的猜想;
(3)在(2)的条件下,当点M运动 秒时,四边形PMNQ是正方形(直接写出结论).
详 解
1.C 2.B 3.B
4.A 解: 对角线相等的四边形推不出是正方形或矩形,故①→②,①→③错误,故选项B,C,D错误.故选A.
5.B 6.C
7.C 解: ①∵F是BC的中点,∴BF=FC.
在 ABCD中,AD=2AB,
∴BC=2AB=2CD,
∴BF=FC=AB,
∴∠AFB=∠BAF.
∵AD∥BC,
∴∠AFB=∠DAF,
∴∠BAF=∠FAD,
∴2∠BAF=∠BAD,故①正确;
②延长EF,交AB的延长线于点M.
∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠MBF=∠C.
∵F为BC的中点,∴BF=CF.
又∵∠BFM=∠CFE,
∴△MBF≌△ECF,∴FE=MF.
∵CE⊥AE,∴∠AEC=90°.
∴∠AEC=∠BAE=90°,
又∵FM=EF,∴EF=AF,故②正确;
③∵EF=FM,∴S△AEF=S△AFM.∵点B与点M不重合,∴S△ABF
∴∠BAF=∠AFB=90°-x,∠EFA=180°-2x,
∴∠EFB=90°-x+180°-2x=270°-3x.
∵∠CEF=90°-x,
∴∠BFE=3∠CEF,故④正确.故选C.
8.48 解: 因为正五边形的一个内角为108°,正三角形的一个内角为60°,所以∠1=48°.
9.20 10.8 11.20
12., 解: 如,连接EC交BD于点P',连接OP'.
∵OP'=CP',∴P'O+P'E=P'C+P'E=CE,此时P'A+P'E的值最小,
∵B(2,0),D(0,2),
∴直线BD的表达式为y=-x+2.
∵E(0,1),C(2,2),
设直线EC的表达式为y=kx+b,则有解得
∴直线EC的表达式为y=x+1.
由解得∴P',.故答案为,.
13.5或6 解: 在矩形ABCD中,AB=CD=4,BC=AD=6.
如①,当PB=PC时,P是BC的垂直平分线与AD的交点,则AP=DP=AD=3.
在Rt△ABP中,由勾股定理,得PB===5;
如②,当BP=BC=6时,△BPC也是以PB为腰的等腰三角形.
综上所述,PB的长度是5或6.
故答案为5或6.
14.证明:(1)∵∠ACB=90°,∠CAB=30°,
∴BC=AB,∠ABC=60°.
∵△ABD是等边三角形,
∴∠ABD=∠BAD=60°,AB=AD,
∴∠ABC=∠BAD,
∴BC∥DA.
∵E是线段AB的中点,
∴CE=AB=BE=AE.
∵∠ABC=60°,
∴△BCE是等边三角形,
则∠BEC=60°=∠ABD,
∴BD∥CF,
∴四边形BCFD为平行四边形.
(2)∵BD∥CF,BE=AE,
∴AF=DF=AD.
又∵BC=DF,
∴BC=AF.
又∵BC∥DA,
∴四边形BCAF是平行四边形.
∵∠ACB=90°,
∴四边形BCAF是矩形.
15.解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
∵AE=CF,
∴BE=DF,
∴四边形DEBF为平行四边形,
∴DE=BF,DE∥BF.
又∵M,N分别是DE,BF的中点,
∴ME=FN,
∴四边形ENFM是平行四边形.
(2)∵四边形ABCD是平行四边形,
∴∠A+∠ABC=180°.
又∵∠ABC=2∠A,
∴3∠A=180°,
∴∠A=60°.
16.证明:如,延长DC到点E,使AM=CE,连接BE.
∵四边形 ABCD是正方形,
∴AB=CB,∠A=∠ABC=∠BCD=90°,
∴∠A=∠BCE=90°,
∴△ABM≌△CBE,
则∠1=∠2,BM=BE.
∵∠MBN=45°,
∴∠1+∠3=45°,
∴∠2+∠3=45°,
∴∠MBN=∠EBN.
又∵BN=BN,BM=BE,
∴△MBN≌△EBN,
∴MN=EN.
∵EN=CE+CN,
∴MN=CE+CN=AM+CN.
17.解:(1)∵四边形OABC是平行四边形,
点A(8,0),B(10,6),
∴C(2,6).
设直线AC的表达式为y=kx+b,
则解得
∴直线AC的表达式为y=-x+8.
(2)猜想:四边形PMNQ是矩形.
证明:如.
∵点C(2,6),
∴直线OC的表达式为y=3x.
设点M,N的运动时间为t秒,
则OM=t,AN=3t,
∴M(t,0),N(8-3t,0).
∵PM,QN垂直于x轴,点P,Q分别在直线OC,AC上,
∴P(t,3t),Q(8-3t,3t).
∴PM=QN=3t.
∵PM∥QN,
∴四边形PMNQ是平行四边形.
又PM⊥x轴,即PM⊥MN,
∴ PMNQ是矩形.
(3)或8
同课章节目录
