北京课改版数学八年级下册同步课时练习:14.3.2 函数图象的画法(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:14.3.2 函数图象的画法(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 10:04:21 | ||
图片预览

文档简介
2.函数象的画法
1.一般来说,函数的象是由平面直角坐标系中的一系列点组成的形.象上每一个点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与它对应的因变量的值.
2.把一个函数的一个自变量的值,和它所对应的因变量的值分别作为一个点的横坐标和纵坐标,就能在平面直角坐标系中描出相应的一个点,由所有这样的点组成的形,就是这个函数的象.
3.由函数表达式画函数象,一般按下列步骤进行:
(1)列表:根据自变量的取值范围列表给出自变量与函数的一些对应值;
(2)描点:以表中对应值为坐标,在坐标平面内描出相应的点;
(3)连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连接起来.
描出的点越多,象越精确.
1.点A(1,m)在函数y=2x的象上,则m的值是 .
2.写出在函数y=x-2的象上的三个点的坐标: 、 、 .
3.下列函数中,象一定经过原点的是 ( )
A.y=3x-2 B.y=
C.y=x2-2x+1 D.y=
4.根据下表中y与x的几组对应值画出的函数象是 ( )
x … -2 -1 0 1 …
y … -3 -2 -1 0 …
5.在平面直角坐标系中,已知点M(2,3),N(-1,-3),P(1,2),Q(-2,3),其中不可能与点A(2,-3)在同一函数象上的是 ( )
A.点M B.点N C.点P D.点Q
6.(1)画出函数y=x2的象;
(2)试判断点(-3,-2)是否在上述函数象上.
7.(1)画出函数y=x3的象;
(2)若点-,m与n,在函数y=x3的象上,直接写出m,n的值.
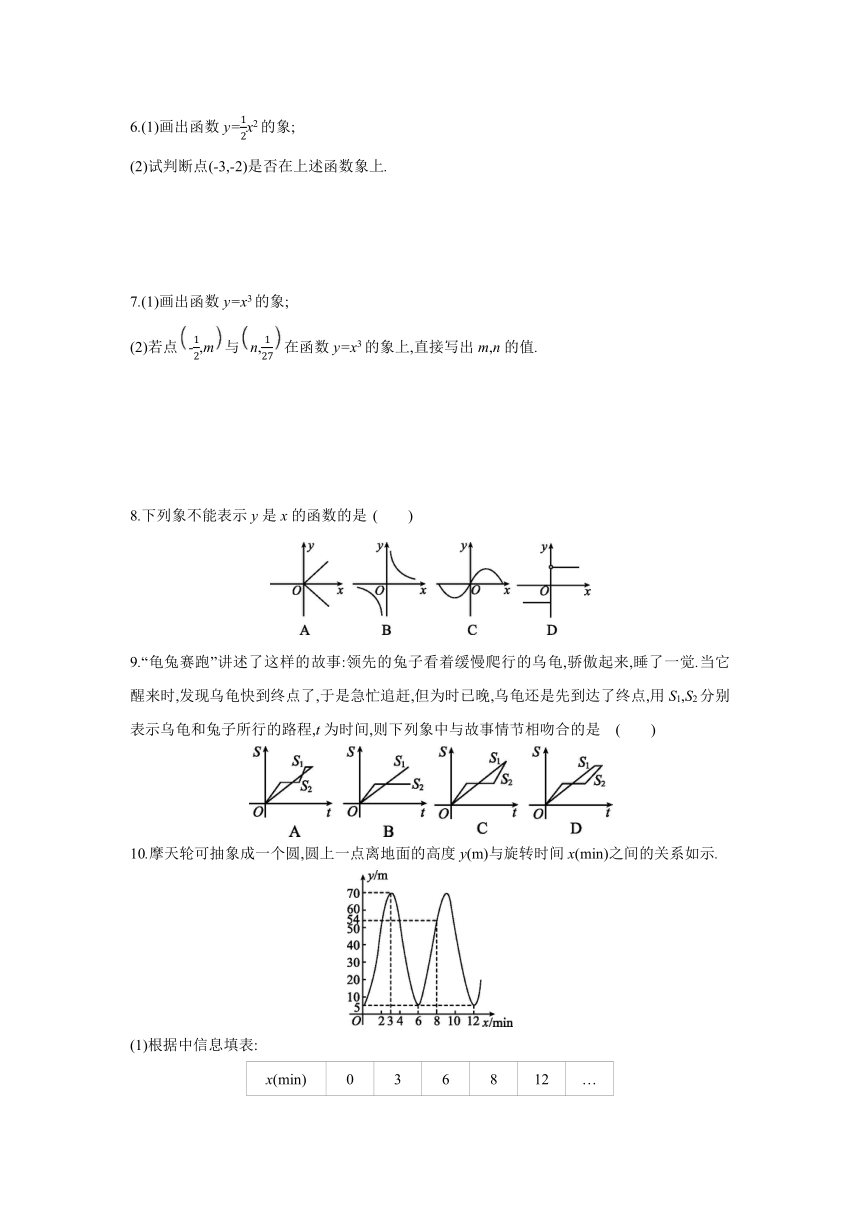
8.下列象不能表示y是x的函数的是 ( )
9.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用S1,S2分别表示乌龟和兔子所行的路程,t为时间,则下列象中与故事情节相吻合的是 ( )
10.摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如示.
(1)根据中信息填表:
x(min) 0 3 6 8 12 …
y(m) …
(2)变量y是x的函数吗 为什么
(3)根据中的信息,请写出摩天轮的直径.
11.小明家所在地的供电公司实行“峰谷电价”,峰时(8:00~21:00)电价为0.5元/度,谷时(21:00~8:00)电价为0.3元/度.为了解空调制暖的耗能情况,小明记录了家里某天0时~24时内空调制暖的用电量,其用电量y(度)与时间x(时)的函数关系如所示.
(1)小明家白天不开空调的时间共 小时;(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为w元,请画出该天0时~24时内w与x的函数象(标注必要数据).
教 师 详 解 详 析
2.函数象的画法
1.2
2.答案不唯一,如:(0,-2) (2,-1) (4,0)
3.D 4.A
5.A 解: 在同一个函数象上,x取某一数值时,y只有唯一的值与它对应,因此点M(2,3)与点A(2,-3)不在同一函数象上.
6.解:(1)列表如下:
x … -3 -2 -1 0 1 2 3 …
y … 4.5 2 0.5 0 0.5 2 4.5 …
描点,连线:
(2)由(1)中列表可知当x=-3时,y=4.5≠-2,∴点(-3,-2)不在函数y=x2的象上.
7.解:(1)列表如下:
x … -2 -1 0 1 2 …
y … -8 -1 0 1 8 …
描点、连线,画出函数象如.
(2)m=-,n=.
8.A
9.D 解: A项,此函数象中,S2先达到最大值,即兔子先到终点,不符合题意;
B项,此函数象中,S2第2段随时间增加其路程一直保持不变,与“当它醒来时,发现乌龟快到终点了,于是急忙追赶”不符,不符合题意;
C项,此函数象中,S1、S2同时到达终点,不符合题意;
D项,S1一直增加;S2有三个阶段,增加,不变,增加,但乌龟还是先到达终点.符合题意.故选D.
10.解:(1)5 70 5 54 5
(2)y是x的函数.理由:由象可知,变量y随着x的变化而变化,同时对于每一个x的值,按照象,变量y都有唯一确定的值与之相对应,符合函数的定义.
(3)摩天轮的直径为70-5=65(m).
11.解:(1)小明家白天不开空调的时间为18-8=10(时).故答案为10.
(2)小明家18时至24时,每小时用电(42-24)÷(24-18)=3(度).所以18时至21时峰时所用电费为(21-18)×3×0.5=4.5(元),0时至8时,21时至24时谷时所用电费为[24+(24-21)×3]×0.3=9.9(元),
所以小明家该天空调制暖所用的电费为4.5+9.9=14.4(元).
(3)根据题意,可得该天0时~24时内w与x的函数象如.
1.一般来说,函数的象是由平面直角坐标系中的一系列点组成的形.象上每一个点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与它对应的因变量的值.
2.把一个函数的一个自变量的值,和它所对应的因变量的值分别作为一个点的横坐标和纵坐标,就能在平面直角坐标系中描出相应的一个点,由所有这样的点组成的形,就是这个函数的象.
3.由函数表达式画函数象,一般按下列步骤进行:
(1)列表:根据自变量的取值范围列表给出自变量与函数的一些对应值;
(2)描点:以表中对应值为坐标,在坐标平面内描出相应的点;
(3)连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连接起来.
描出的点越多,象越精确.
1.点A(1,m)在函数y=2x的象上,则m的值是 .
2.写出在函数y=x-2的象上的三个点的坐标: 、 、 .
3.下列函数中,象一定经过原点的是 ( )
A.y=3x-2 B.y=
C.y=x2-2x+1 D.y=
4.根据下表中y与x的几组对应值画出的函数象是 ( )
x … -2 -1 0 1 …
y … -3 -2 -1 0 …
5.在平面直角坐标系中,已知点M(2,3),N(-1,-3),P(1,2),Q(-2,3),其中不可能与点A(2,-3)在同一函数象上的是 ( )
A.点M B.点N C.点P D.点Q
6.(1)画出函数y=x2的象;
(2)试判断点(-3,-2)是否在上述函数象上.
7.(1)画出函数y=x3的象;
(2)若点-,m与n,在函数y=x3的象上,直接写出m,n的值.
8.下列象不能表示y是x的函数的是 ( )
9.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用S1,S2分别表示乌龟和兔子所行的路程,t为时间,则下列象中与故事情节相吻合的是 ( )
10.摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如示.
(1)根据中信息填表:
x(min) 0 3 6 8 12 …
y(m) …
(2)变量y是x的函数吗 为什么
(3)根据中的信息,请写出摩天轮的直径.
11.小明家所在地的供电公司实行“峰谷电价”,峰时(8:00~21:00)电价为0.5元/度,谷时(21:00~8:00)电价为0.3元/度.为了解空调制暖的耗能情况,小明记录了家里某天0时~24时内空调制暖的用电量,其用电量y(度)与时间x(时)的函数关系如所示.
(1)小明家白天不开空调的时间共 小时;(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为w元,请画出该天0时~24时内w与x的函数象(标注必要数据).
教 师 详 解 详 析
2.函数象的画法
1.2
2.答案不唯一,如:(0,-2) (2,-1) (4,0)
3.D 4.A
5.A 解: 在同一个函数象上,x取某一数值时,y只有唯一的值与它对应,因此点M(2,3)与点A(2,-3)不在同一函数象上.
6.解:(1)列表如下:
x … -3 -2 -1 0 1 2 3 …
y … 4.5 2 0.5 0 0.5 2 4.5 …
描点,连线:
(2)由(1)中列表可知当x=-3时,y=4.5≠-2,∴点(-3,-2)不在函数y=x2的象上.
7.解:(1)列表如下:
x … -2 -1 0 1 2 …
y … -8 -1 0 1 8 …
描点、连线,画出函数象如.
(2)m=-,n=.
8.A
9.D 解: A项,此函数象中,S2先达到最大值,即兔子先到终点,不符合题意;
B项,此函数象中,S2第2段随时间增加其路程一直保持不变,与“当它醒来时,发现乌龟快到终点了,于是急忙追赶”不符,不符合题意;
C项,此函数象中,S1、S2同时到达终点,不符合题意;
D项,S1一直增加;S2有三个阶段,增加,不变,增加,但乌龟还是先到达终点.符合题意.故选D.
10.解:(1)5 70 5 54 5
(2)y是x的函数.理由:由象可知,变量y随着x的变化而变化,同时对于每一个x的值,按照象,变量y都有唯一确定的值与之相对应,符合函数的定义.
(3)摩天轮的直径为70-5=65(m).
11.解:(1)小明家白天不开空调的时间为18-8=10(时).故答案为10.
(2)小明家18时至24时,每小时用电(42-24)÷(24-18)=3(度).所以18时至21时峰时所用电费为(21-18)×3×0.5=4.5(元),0时至8时,21时至24时谷时所用电费为[24+(24-21)×3]×0.3=9.9(元),
所以小明家该天空调制暖所用的电费为4.5+9.9=14.4(元).
(3)根据题意,可得该天0时~24时内w与x的函数象如.
同课章节目录
