北京课改版数学八年级下册同步课时练习:14.7 第2课时 一次函数与方程、不等式的关系(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:14.7 第2课时 一次函数与方程、不等式的关系(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 163.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 10:08:21 | ||
图片预览


文档简介
第2课时 一次函数与方程、不等式的关系
1.每个二元一次方程都对应一个一次函数,且以它的每一个解为坐标的点均在相应的一次函数的象上;反之,任意一个一次函数象上的每一个点的坐标均是相应二元一次方程的解.
2.两个一次函数象的交点坐标是对应的二元一次方程组的解.
3.求一元一次不等式ax+b>0或ax+b<0的解相当于在对应的一次函数y=ax+b的函数值大于0或小于0时,求自变量x的取值范围.
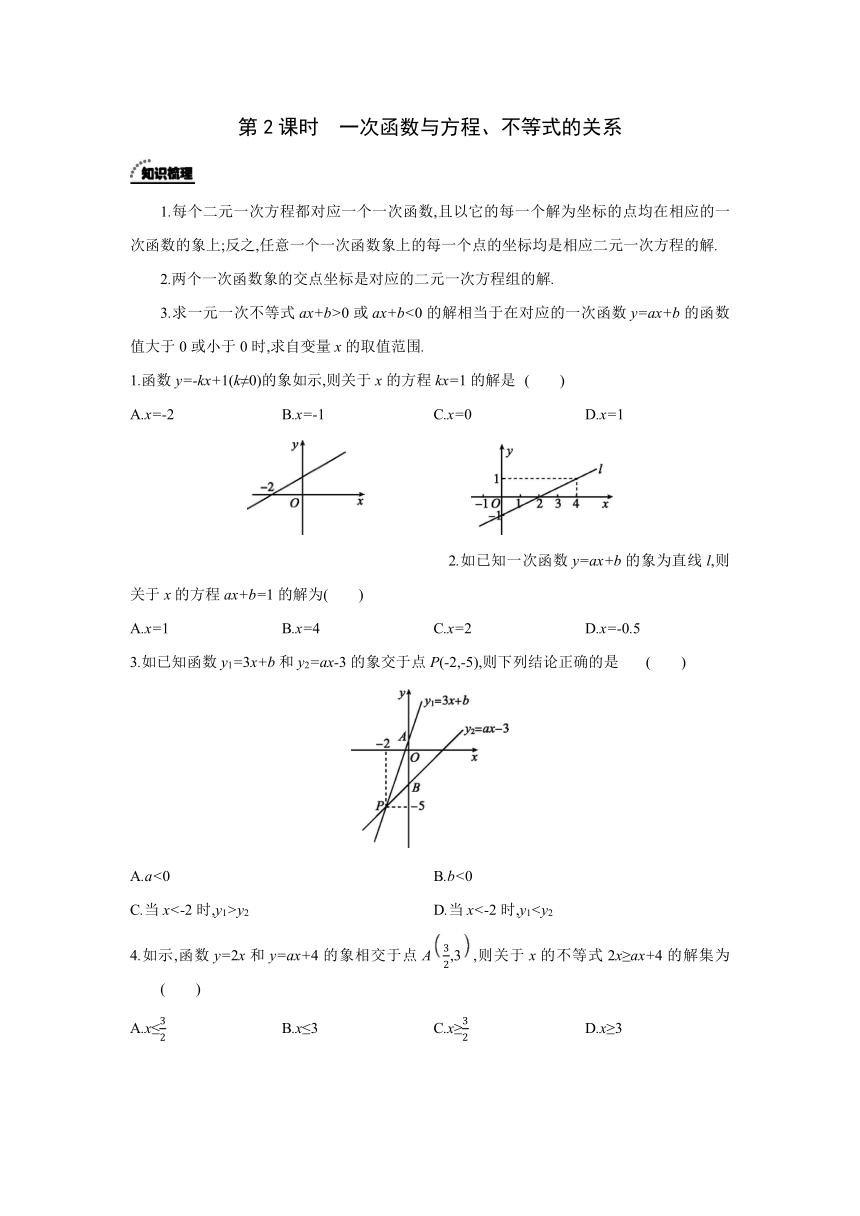
1.函数y=-kx+1(k≠0)的象如示,则关于x的方程kx=1的解是 ( )
A.x=-2 B.x=-1 C.x=0 D.x=1
2.如已知一次函数y=ax+b的象为直线l,则关于x的方程ax+b=1的解为( )
A.x=1 B.x=4 C.x=2 D.x=-0.5
3.如已知函数y1=3x+b和y2=ax-3的象交于点P(-2,-5),则下列结论正确的是 ( )
A.a<0 B.b<0
C.当x<-2时,y1>y2 D.当x<-2时,y14.如示,函数y=2x和y=ax+4的象相交于点A,3,则关于x的不等式2x≥ax+4的解集为 ( )
A.x≤ B.x≤3 C.x≥ D.x≥3
5.如l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系.根据象判断,该公司盈利时,销售量 ( )
A.小于12件 B.等于12件 C.大于12件 D.不低于12件
6.如,一次函数y=kx+b(k≠0)的象经过A,B两点.
(1)求该一次函数的表达式;
(2)结合函数象,直接写出关于x的不等式kx+b<4的解集.
7.已知一次函数y=ax+2与y=kx+b的象如所示,且二元一次方程组的解为点B的坐标为(0,-1).求这两个一次函数的表达式.
8.如,已知一次函数y=kx+k+1的象与一次函数y=-x+4的象交于点A(1,a).
(1)求a,k的值;
(2)根据象,写出不等式-x+4>kx+k+1的解集;
(3)结合象,当x>2时,求一次函数y=-x+4的函数值y的取值范围.
9.如,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值,并结合象直接写出关于x,y的方程组的解;
(2)垂直于x轴的直线x=a与直线l1,l2分别交于点C,D,若线段CD的长为2,求a的值.
10.在平面直角坐标系xOy中,一次函数y1=k1x+4m(m≠0)的象l1经过点B(p,2m).
(1)当m=1,k1=-1,且正比例函数y2=k2x的象l2经过点B时.
①若y1②若一次函数y3=k3x+1的象为l3,且l1,l2,l3不能围成三角形,求k3的值.
(2)若直线l1与x轴交于点C(n,0),且n+2p=4m,求m,n的数量关系.
教 师 详 解 详 析
第2课时 一次函数与方程、不等式的关系
1.A 2.B 3.D 4.C
5.C 解: 该公司盈利时,即销售收入大于销售成本,需要l1在l2的上方,即x>12,即销售量大于12件.
6.解:(1)将点A(3,4),B(0,-2)分别代入y=kx+b中,
得解得
故该一次函数的表达式为y=2x-2.
(2)观察象可知关于x的不等式kx+b<4的解集为x<3.
7.解:由题意可得A(2,1).
把点A的坐标代入y=ax+2,得1=2a+2,
解得a=-,所以y=-x+2.
把点A,B的坐标分别代入y=kx+b,
得解得
所以y=x-1.
故两个一次函数的表达式分别为y=-x+2,y=x-1.
8.解:(1)把A(1,a)代入y=-x+4,得a=-1+4=3,将A(1,3)代入y=kx+k+1,得k+k+1=3,解得k=1.
(2)不等式-x+4>kx+k+1的解集为x<1.
(3)当x=2时,y=-x+4=-2+4=2,所以当x>2时,y<2.
9.解:(1)因为点P(1,b)在直线l1:y=2x+1上,
所以b=2×1+1=3,所以P(1,3).
因为点P(1,3)在直线l2:y=mx+4上,
所以3=m+4,
所以m=-1.
由象可知关于x,y的方程组的解为
(2)当x=a时,yC=2a+1,yD=4-a.
因为CD=2,所以|2a+1-(4-a)|=2,
解得a=或a=,所以a的值为或.
10.解:(1)因为一次函数y1=k1x+4m(m≠0)的象l1经过点B(p,2m),
所以2m=k1p+4m,所以k1p=-2m.
因为m=1,k1=-1,所以一次函数的表达式为y1=-x+4,p=2,所以B(2,2).
把B(2,2)代入y2=k2x中,可得k2=1,
所以正比例函数的表达式为y2=x.
因为①若y12.
②若l1,l2,l3不能围成三角形,则l3∥l1或l3∥l2或l3经过l1与l2的交点.
由题意,可知l1与l2的交点坐标为B(2,2).
将(2,2)代入y3=k3x+1,得2=2k3+1,解得k3=,
所以k3的值为-1或1或.
(2)因为一次函数y1=k1x+4m(m≠0)的象l1经过点B(p,2m),所以pk1+4m=2m①.
因为直线l1与x轴交于点C(n,0),
所以nk1+4m=0②,
联立①②,可解得p=n.
因为n+2p=4m,所以n=2m.
1.每个二元一次方程都对应一个一次函数,且以它的每一个解为坐标的点均在相应的一次函数的象上;反之,任意一个一次函数象上的每一个点的坐标均是相应二元一次方程的解.
2.两个一次函数象的交点坐标是对应的二元一次方程组的解.
3.求一元一次不等式ax+b>0或ax+b<0的解相当于在对应的一次函数y=ax+b的函数值大于0或小于0时,求自变量x的取值范围.
1.函数y=-kx+1(k≠0)的象如示,则关于x的方程kx=1的解是 ( )
A.x=-2 B.x=-1 C.x=0 D.x=1
2.如已知一次函数y=ax+b的象为直线l,则关于x的方程ax+b=1的解为( )
A.x=1 B.x=4 C.x=2 D.x=-0.5
3.如已知函数y1=3x+b和y2=ax-3的象交于点P(-2,-5),则下列结论正确的是 ( )
A.a<0 B.b<0
C.当x<-2时,y1>y2 D.当x<-2时,y1
A.x≤ B.x≤3 C.x≥ D.x≥3
5.如l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系.根据象判断,该公司盈利时,销售量 ( )
A.小于12件 B.等于12件 C.大于12件 D.不低于12件
6.如,一次函数y=kx+b(k≠0)的象经过A,B两点.
(1)求该一次函数的表达式;
(2)结合函数象,直接写出关于x的不等式kx+b<4的解集.
7.已知一次函数y=ax+2与y=kx+b的象如所示,且二元一次方程组的解为点B的坐标为(0,-1).求这两个一次函数的表达式.
8.如,已知一次函数y=kx+k+1的象与一次函数y=-x+4的象交于点A(1,a).
(1)求a,k的值;
(2)根据象,写出不等式-x+4>kx+k+1的解集;
(3)结合象,当x>2时,求一次函数y=-x+4的函数值y的取值范围.
9.如,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值,并结合象直接写出关于x,y的方程组的解;
(2)垂直于x轴的直线x=a与直线l1,l2分别交于点C,D,若线段CD的长为2,求a的值.
10.在平面直角坐标系xOy中,一次函数y1=k1x+4m(m≠0)的象l1经过点B(p,2m).
(1)当m=1,k1=-1,且正比例函数y2=k2x的象l2经过点B时.
①若y1
(2)若直线l1与x轴交于点C(n,0),且n+2p=4m,求m,n的数量关系.
教 师 详 解 详 析
第2课时 一次函数与方程、不等式的关系
1.A 2.B 3.D 4.C
5.C 解: 该公司盈利时,即销售收入大于销售成本,需要l1在l2的上方,即x>12,即销售量大于12件.
6.解:(1)将点A(3,4),B(0,-2)分别代入y=kx+b中,
得解得
故该一次函数的表达式为y=2x-2.
(2)观察象可知关于x的不等式kx+b<4的解集为x<3.
7.解:由题意可得A(2,1).
把点A的坐标代入y=ax+2,得1=2a+2,
解得a=-,所以y=-x+2.
把点A,B的坐标分别代入y=kx+b,
得解得
所以y=x-1.
故两个一次函数的表达式分别为y=-x+2,y=x-1.
8.解:(1)把A(1,a)代入y=-x+4,得a=-1+4=3,将A(1,3)代入y=kx+k+1,得k+k+1=3,解得k=1.
(2)不等式-x+4>kx+k+1的解集为x<1.
(3)当x=2时,y=-x+4=-2+4=2,所以当x>2时,y<2.
9.解:(1)因为点P(1,b)在直线l1:y=2x+1上,
所以b=2×1+1=3,所以P(1,3).
因为点P(1,3)在直线l2:y=mx+4上,
所以3=m+4,
所以m=-1.
由象可知关于x,y的方程组的解为
(2)当x=a时,yC=2a+1,yD=4-a.
因为CD=2,所以|2a+1-(4-a)|=2,
解得a=或a=,所以a的值为或.
10.解:(1)因为一次函数y1=k1x+4m(m≠0)的象l1经过点B(p,2m),
所以2m=k1p+4m,所以k1p=-2m.
因为m=1,k1=-1,所以一次函数的表达式为y1=-x+4,p=2,所以B(2,2).
把B(2,2)代入y2=k2x中,可得k2=1,
所以正比例函数的表达式为y2=x.
因为①若y1
②若l1,l2,l3不能围成三角形,则l3∥l1或l3∥l2或l3经过l1与l2的交点.
由题意,可知l1与l2的交点坐标为B(2,2).
将(2,2)代入y3=k3x+1,得2=2k3+1,解得k3=,
所以k3的值为-1或1或.
(2)因为一次函数y1=k1x+4m(m≠0)的象l1经过点B(p,2m),所以pk1+4m=2m①.
因为直线l1与x轴交于点C(n,0),
所以nk1+4m=0②,
联立①②,可解得p=n.
因为n+2p=4m,所以n=2m.
同课章节目录
