北京课改版数学八年级下册同步课时练习:15.3.1 第1课时 平行四边形边和角的性质(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:15.3.1 第1课时 平行四边形边和角的性质(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 208.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览



文档简介
15.3 1.第1课时 平行四边形边和角的性质
1.由平行四边形的定义可知平行四边形的两组对边分别平行.
2.平行四边形性质定理1:
平行四边形的对边相等.
符号语言:如
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
3.平行四边形性质定理2:
平行四边形的对角相等.
符号语言:如
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D.
4.推论1:夹在两条平行线间的平行线段相等.
推论2:平行直线间的距离处处相等.
1.(2020丰台区期末改编)在 ABCD中,∠A+∠C=100°,则∠A的度数为 ( )
A.60° B.80° C.50° D.20°
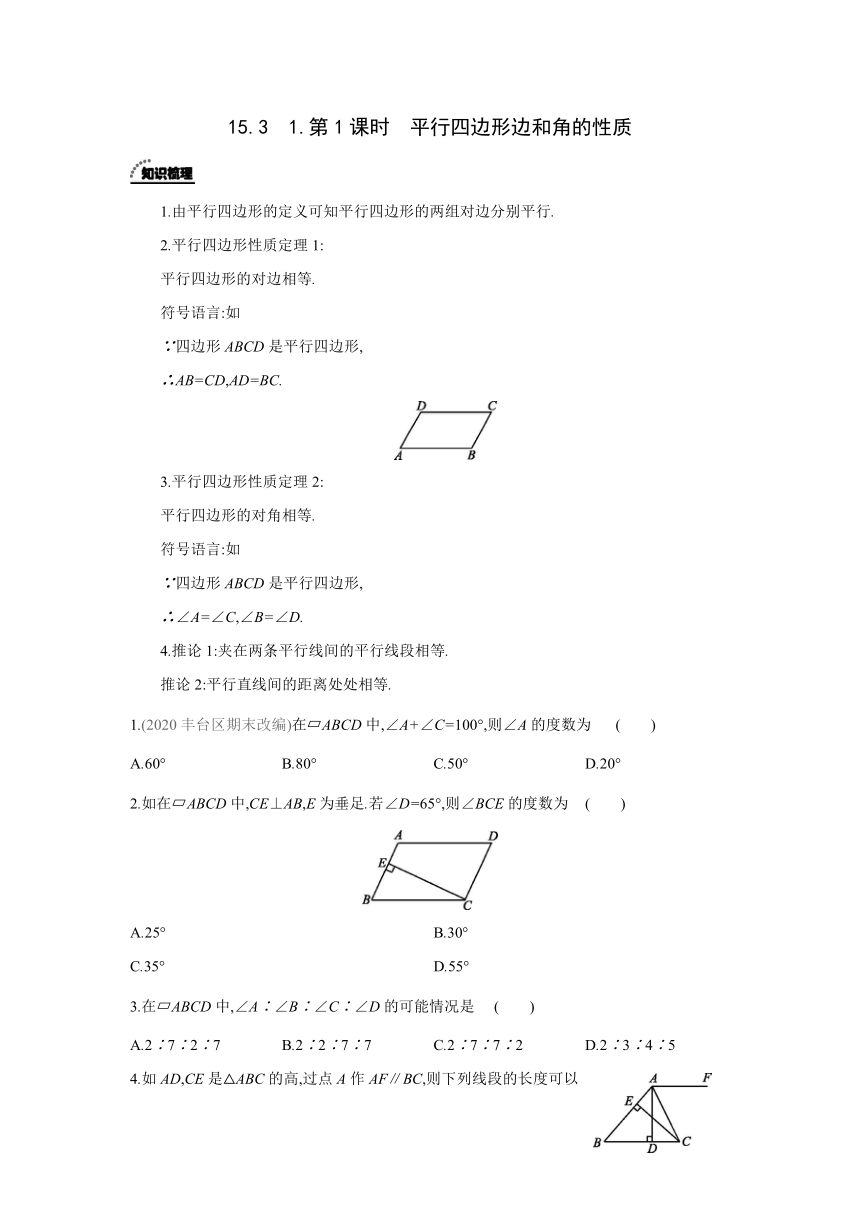
2.如在 ABCD中,CE⊥AB,E为垂足.若∠D=65°,则∠BCE的度数为 ( )
A.25° B.30°
C.35° D.55°
3.在 ABCD中,∠A∶∠B∶∠C∶∠D的可能情况是 ( )
A.2∶7∶2∶7 B.2∶2∶7∶7 C.2∶7∶7∶2 D.2∶3∶4∶5
4.如AD,CE是△ABC的高,过点A作AF∥BC,则下列线段的长度可以表示中两条平行线之间的距离的是 ( )
A.AB B.AD
C.CE D.AC 5.已知 ABCD的周长为24,△ABD的周长为19,则对角线BD的长是 ( )
A.4 B.5 C.6 D.7
6.平行四边形的周长为24 cm,相邻两边长的差为2 cm,则平行四边形相邻两边的长为 ( )
A.4 cm,8 cm B.5 cm,7 cm C.5.5 cm,6.5 cm D.3 cm,9 cm
7.如示,在 ABCD中,对角线AC,BD相交于点O,则中全等三角形共有 对.
8.如在 ABCD中,AC⊥AB.若BC=10,AC=8,则AD= ,DC= .
9.在 ABCD中,AB=8 cm,BC=10 cm,∠B=30°,则S ABCD= .
10.如在 ABCD中,E,F是直线BD上的两点,且BF=DE,连接AE,CF.
(1)如①,求证:AE=CF;
(2)如②,请直接写出AE,CF的位置关系.
11.如已知l1∥l2,点C1在l1上,C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请你帮小颖说明理由.
12.(2020东城区期末)如在等腰三角形ABC中,P是底边BC上的动点(不与点B,C重合),过点P分别作AB,AC的平行线PM,PN交AC,AB于点M,N,则下列数量关系一定正确的是( )
A.PM+PN=AB B.PM+PN=BC
C.PM+PN=2BC D.PM+PN=AB+BC 13.如在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:DF=CE;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
14.我们把能平分四边形面积的直线称为“好线”.利用下面的作,可以得到四边形的“好线”:如①,在四边形ABCD中,取对角线BD的中点O,连接OA,OC,显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于点E,则直线AE即为一条“好线”.
(1)试说明直线AE是“好线”;
(2)如②,AE为一条“好线”,F为AD边上的一点,请作出经过点F的“好线”,并对画进行适当说明.
教 师 详 解 详 析
15.3 1.第1课时 平行四边形边和角的性质
1.C 解: ∵四边形ABCD是平行四边形,∴∠A=∠C.又∵∠A+∠C=100°,
∴∠A=50°.故答案为C.
2.A 解: ∵四边形ABCD是平行四边形,
∴∠B=∠D=65°.
∵CE⊥AB,
∴∠CEB=90°,
∴∠BCE=90°-65°=25°.
3.A
4.B 解: 由于AF∥BC,且AD⊥BC于点D,因此AD的长度是平行线AF与BC之间的距离.
5.D 解: ∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,
∴2(AB+AD)=24,
∴AB+AD=12.
又∵△ABD的周长为19,
∴AB+AD+BD=19,即12+BD=19,
∴BD=7.
6.B
7.4
8.10 6 解: ∵四边形ABCD是平行四边形,
∴DC=AB,AD=BC=10.
∵AC⊥AB,BC=10,AC=8,
∴DC=AB=6.
9.40 cm2
10.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠ABE=∠CDF.
∵BF=DE,∴BE=DF,
∴△ABE≌△CDF,∴AE=CF.
(2)AE∥CF.
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADB=∠CBD.
又∵BF=DE,∴△ADE≌△CBF,
∴∠E=∠F,∴AE∥CF.
11.解:理由:∵直线l1∥l2,
∴△ABC1,△ABC2,△ABC3的底边AB上的高相等,
∴△ABC1,△ABC2,△ABC3这三个三角形同底等高,
∴△ABC1,△ABC2,△ABC3这三个三角形的面积相等,即S1=S2=S3.
12.A 解: ∵AB=AC,∴∠B=∠C.
∵PN∥AC,∴∠BPN=∠C=∠B,
∴PN=BN.∵PM∥AB,PN∥AC,
∴四边形AMPN是平行四边形,∴PM=AN,
∴PM+PN=AN+BN=AB.
13.解:(1)证明:∵四边形ABCD是平行四边形,∴AD=BC.
∵F是AD的中点,
∴DF=AD.
又∵CE=BC,∴DF=CE.
(2)如,过点D作DH⊥BE于点H.
∵四边形ABCD是平行四边形,
∴AB∥DC,CD=AB=4,
∴∠B=∠DCE=60°,
∴∠CDH=30°,
∴CH=CD=2,则DH=2.
∵CE=DF=AD=3,
∴EH=1,
∴在Rt△DHE中,根据勾股定理,得DE===.
14.解:(1)∵OE∥AC,
∴S△AOC=S△ACE,S△AOE=S△OCE,
∴S△AOF=S△CEF.
又∵O为BD的中点,
∴折线AOC能平分四边形ABCD的面积,
∴直线AE平分四边形ABCD的面积,
即直线AE是“好线”.
(2)如,连接EF,过点A作EF的平行线交CD于点G,连接GF,则GF为一条“好线”.
∵AG∥EF,
∴S△AGE=S△AFG.
设AE与FG的交点是O,则S△AOF=S△GOE.
又∵AE为一条“好线”,
∴GF为一条“好线”.
1.由平行四边形的定义可知平行四边形的两组对边分别平行.
2.平行四边形性质定理1:
平行四边形的对边相等.
符号语言:如
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
3.平行四边形性质定理2:
平行四边形的对角相等.
符号语言:如
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D.
4.推论1:夹在两条平行线间的平行线段相等.
推论2:平行直线间的距离处处相等.
1.(2020丰台区期末改编)在 ABCD中,∠A+∠C=100°,则∠A的度数为 ( )
A.60° B.80° C.50° D.20°
2.如在 ABCD中,CE⊥AB,E为垂足.若∠D=65°,则∠BCE的度数为 ( )
A.25° B.30°
C.35° D.55°
3.在 ABCD中,∠A∶∠B∶∠C∶∠D的可能情况是 ( )
A.2∶7∶2∶7 B.2∶2∶7∶7 C.2∶7∶7∶2 D.2∶3∶4∶5
4.如AD,CE是△ABC的高,过点A作AF∥BC,则下列线段的长度可以表示中两条平行线之间的距离的是 ( )
A.AB B.AD
C.CE D.AC 5.已知 ABCD的周长为24,△ABD的周长为19,则对角线BD的长是 ( )
A.4 B.5 C.6 D.7
6.平行四边形的周长为24 cm,相邻两边长的差为2 cm,则平行四边形相邻两边的长为 ( )
A.4 cm,8 cm B.5 cm,7 cm C.5.5 cm,6.5 cm D.3 cm,9 cm
7.如示,在 ABCD中,对角线AC,BD相交于点O,则中全等三角形共有 对.
8.如在 ABCD中,AC⊥AB.若BC=10,AC=8,则AD= ,DC= .
9.在 ABCD中,AB=8 cm,BC=10 cm,∠B=30°,则S ABCD= .
10.如在 ABCD中,E,F是直线BD上的两点,且BF=DE,连接AE,CF.
(1)如①,求证:AE=CF;
(2)如②,请直接写出AE,CF的位置关系.
11.如已知l1∥l2,点C1在l1上,C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请你帮小颖说明理由.
12.(2020东城区期末)如在等腰三角形ABC中,P是底边BC上的动点(不与点B,C重合),过点P分别作AB,AC的平行线PM,PN交AC,AB于点M,N,则下列数量关系一定正确的是( )
A.PM+PN=AB B.PM+PN=BC
C.PM+PN=2BC D.PM+PN=AB+BC 13.如在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:DF=CE;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
14.我们把能平分四边形面积的直线称为“好线”.利用下面的作,可以得到四边形的“好线”:如①,在四边形ABCD中,取对角线BD的中点O,连接OA,OC,显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于点E,则直线AE即为一条“好线”.
(1)试说明直线AE是“好线”;
(2)如②,AE为一条“好线”,F为AD边上的一点,请作出经过点F的“好线”,并对画进行适当说明.
教 师 详 解 详 析
15.3 1.第1课时 平行四边形边和角的性质
1.C 解: ∵四边形ABCD是平行四边形,∴∠A=∠C.又∵∠A+∠C=100°,
∴∠A=50°.故答案为C.
2.A 解: ∵四边形ABCD是平行四边形,
∴∠B=∠D=65°.
∵CE⊥AB,
∴∠CEB=90°,
∴∠BCE=90°-65°=25°.
3.A
4.B 解: 由于AF∥BC,且AD⊥BC于点D,因此AD的长度是平行线AF与BC之间的距离.
5.D 解: ∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,
∴2(AB+AD)=24,
∴AB+AD=12.
又∵△ABD的周长为19,
∴AB+AD+BD=19,即12+BD=19,
∴BD=7.
6.B
7.4
8.10 6 解: ∵四边形ABCD是平行四边形,
∴DC=AB,AD=BC=10.
∵AC⊥AB,BC=10,AC=8,
∴DC=AB=6.
9.40 cm2
10.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠ABE=∠CDF.
∵BF=DE,∴BE=DF,
∴△ABE≌△CDF,∴AE=CF.
(2)AE∥CF.
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADB=∠CBD.
又∵BF=DE,∴△ADE≌△CBF,
∴∠E=∠F,∴AE∥CF.
11.解:理由:∵直线l1∥l2,
∴△ABC1,△ABC2,△ABC3的底边AB上的高相等,
∴△ABC1,△ABC2,△ABC3这三个三角形同底等高,
∴△ABC1,△ABC2,△ABC3这三个三角形的面积相等,即S1=S2=S3.
12.A 解: ∵AB=AC,∴∠B=∠C.
∵PN∥AC,∴∠BPN=∠C=∠B,
∴PN=BN.∵PM∥AB,PN∥AC,
∴四边形AMPN是平行四边形,∴PM=AN,
∴PM+PN=AN+BN=AB.
13.解:(1)证明:∵四边形ABCD是平行四边形,∴AD=BC.
∵F是AD的中点,
∴DF=AD.
又∵CE=BC,∴DF=CE.
(2)如,过点D作DH⊥BE于点H.
∵四边形ABCD是平行四边形,
∴AB∥DC,CD=AB=4,
∴∠B=∠DCE=60°,
∴∠CDH=30°,
∴CH=CD=2,则DH=2.
∵CE=DF=AD=3,
∴EH=1,
∴在Rt△DHE中,根据勾股定理,得DE===.
14.解:(1)∵OE∥AC,
∴S△AOC=S△ACE,S△AOE=S△OCE,
∴S△AOF=S△CEF.
又∵O为BD的中点,
∴折线AOC能平分四边形ABCD的面积,
∴直线AE平分四边形ABCD的面积,
即直线AE是“好线”.
(2)如,连接EF,过点A作EF的平行线交CD于点G,连接GF,则GF为一条“好线”.
∵AG∥EF,
∴S△AGE=S△AFG.
设AE与FG的交点是O,则S△AOF=S△GOE.
又∵AE为一条“好线”,
∴GF为一条“好线”.
同课章节目录
