北京课改版数学八年级下册同步课时练习:15.2 平行四边形和特殊的平行四边形(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:15.2 平行四边形和特殊的平行四边形(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 277.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 10:15:00 | ||
图片预览

文档简介
二 15.2 平行四边形和特殊的平行四边形
1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形的表示:
平行四边形用符号“ ”表示,如示,“平行四边形ABCD”可以记作“ ABCD”.
2.矩形的定义:有一个角是直角的平行四边形叫做矩形.
3.菱形的定义:有一组邻边相等的平行四边形叫做菱形.
4.正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
1.已知AB∥CD,AD∥BC,则四边形ABCD是 ( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2.小明和小亮在做一道习题,若四边形ABCD是平行四边形,请补充条件,使得四边形ABCD是菱形.小明补充的条件是AB=BC,小亮补充的条件是AB=CD,则下列说法正确的是 ( )
A.小明、小亮都正确 B.小明正确,小亮错误
C.小明错误,小亮正确 D.小明、小亮都错误
3.如在矩形ABCD中,若添加一个条件可以得到四边形ABCD是正方形,则这个条件是 ( )
A.∠C=90° B.AD=BC
C.AD=CD D.∠A=90°
4.如已知四边形ABCD是平行四边形,若再从①AB=BC,
②∠B=90°,③AD=BC,④∠D=90°四个条件中,选两个作为补充条件,使得四边形ABCD是正方形,则下列四种选法,其中正确的是 ( )
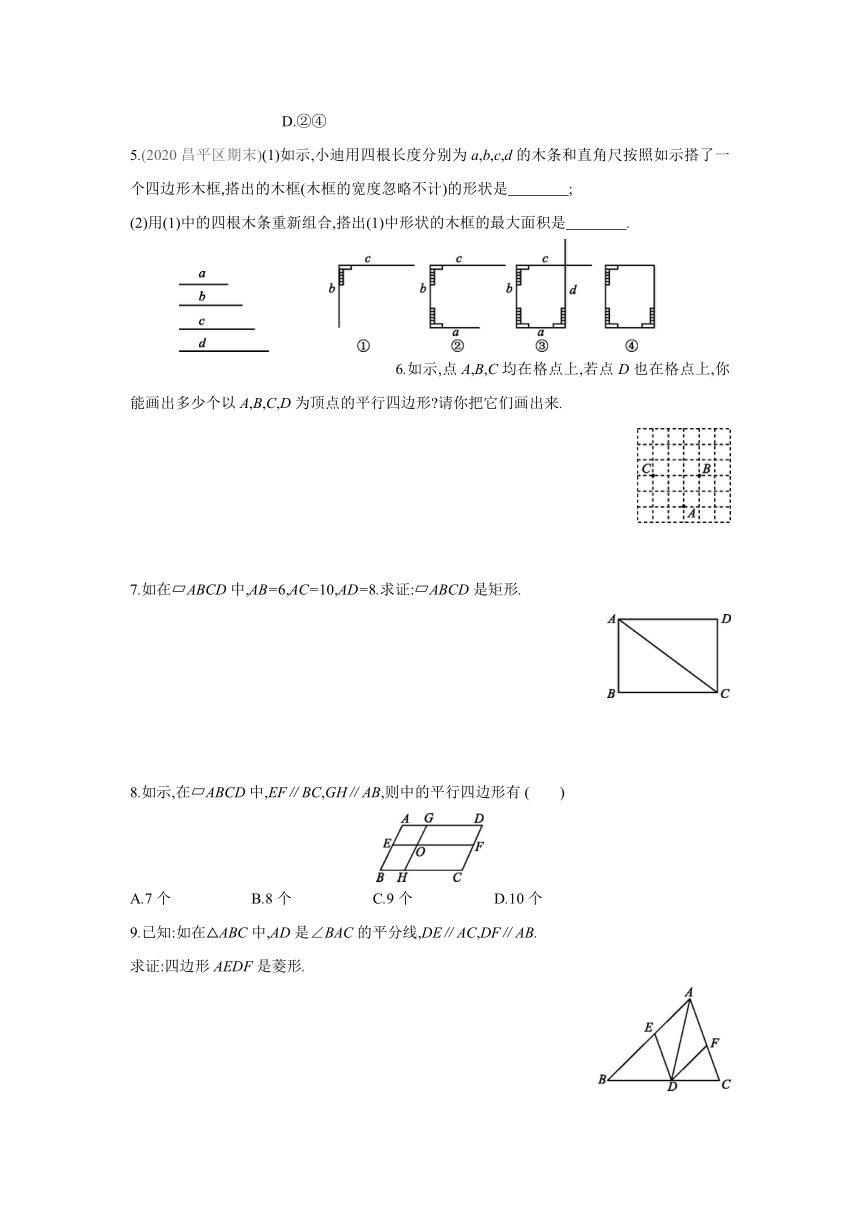
A.①③ B.②③ C.①④ D.②④
5.(2020昌平区期末)(1)如示,小迪用四根长度分别为a,b,c,d的木条和直角尺按照如示搭了一个四边形木框,搭出的木框(木框的宽度忽略不计)的形状是 ;
(2)用(1)中的四根木条重新组合,搭出(1)中形状的木框的最大面积是 .
6.如示,点A,B,C均在格点上,若点D也在格点上,你能画出多少个以A,B,C,D为顶点的平行四边形 请你把它们画出来.
7.如在 ABCD中,AB=6,AC=10,AD=8.求证: ABCD是矩形.
8.如示,在 ABCD中,EF∥BC,GH∥AB,则中的平行四边形有 ( )
A.7个 B.8个 C.9个 D.10个
9.已知:如在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形.
10.如,在矩形ABCD中,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以每秒3 cm的速度向点B移动,点Q以每秒2 cm的速度向点D移动,当点P到达点B时,两点均停止移动.是否存在某一时刻,使四边形PBCQ为正方形 若存在,求出该时刻;若不存在,请说明理由.
11.如①所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长分别为1和2,另一种纸片的两条直角边长都为2.②,③,④是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请用三种方法将中所给的四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,三种方法所拼得的平行四边形(非矩形)的周长互不相等,并把你所拼得的形分别画在②,③,④的方格纸上.
要求:(1)所画形各顶点必须与方格纸中的小正方形顶点重合;
(2)画时,要保留四块直角三角形纸片的拼接痕迹.
教 师 详 解 详 析
二 15.2 平行四边形和特殊的平行四边形
1.A 2.B 3.C
4.C 解: 有一组邻边相等且有一个角是直角的平行四边形是正方形,选项C符合题意.
5.(1)矩形 (2)ac 解: (1)根据三个角是直角的四边形是矩形可得搭出的木框(木框的宽度忽略不计)的形状是矩形;(2)用(1)中的四根木条重新组合,搭出(1)中形状的木框的最大面积是ac.
6.解:3个,略.
7.证明:∵四边形ABCD为平行四边形,
∴BC=AD=8.
∵AB2+BC2=100,AC2=100,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
则∠ABC=90°,
∴ ABCD是矩形.
8.C
9.证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵AD平分∠BAC,
∴∠EAD=∠FAD(角平分线的定义).
∵DE∥AC,
∴∠FAD=∠EDA(两直线平行,内错角相等),
∴∠EAD=∠EDA(等量代换),
∴AE=DE,
∴四边形AEDF是菱形.
10.解:不存在.理由:设存在某时刻t,使得四边形PBCQ是正方形,则BP=CQ,即16-3t=2t,解得t=,∴CQ=2t=≠6,即CQ≠CB,
∴四边形PBCQ是正方形不成立.
故不存在某一时刻,使四边形PBCQ为正方形.
11.解:如.
1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形的表示:
平行四边形用符号“ ”表示,如示,“平行四边形ABCD”可以记作“ ABCD”.
2.矩形的定义:有一个角是直角的平行四边形叫做矩形.
3.菱形的定义:有一组邻边相等的平行四边形叫做菱形.
4.正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
1.已知AB∥CD,AD∥BC,则四边形ABCD是 ( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2.小明和小亮在做一道习题,若四边形ABCD是平行四边形,请补充条件,使得四边形ABCD是菱形.小明补充的条件是AB=BC,小亮补充的条件是AB=CD,则下列说法正确的是 ( )
A.小明、小亮都正确 B.小明正确,小亮错误
C.小明错误,小亮正确 D.小明、小亮都错误
3.如在矩形ABCD中,若添加一个条件可以得到四边形ABCD是正方形,则这个条件是 ( )
A.∠C=90° B.AD=BC
C.AD=CD D.∠A=90°
4.如已知四边形ABCD是平行四边形,若再从①AB=BC,
②∠B=90°,③AD=BC,④∠D=90°四个条件中,选两个作为补充条件,使得四边形ABCD是正方形,则下列四种选法,其中正确的是 ( )
A.①③ B.②③ C.①④ D.②④
5.(2020昌平区期末)(1)如示,小迪用四根长度分别为a,b,c,d的木条和直角尺按照如示搭了一个四边形木框,搭出的木框(木框的宽度忽略不计)的形状是 ;
(2)用(1)中的四根木条重新组合,搭出(1)中形状的木框的最大面积是 .
6.如示,点A,B,C均在格点上,若点D也在格点上,你能画出多少个以A,B,C,D为顶点的平行四边形 请你把它们画出来.
7.如在 ABCD中,AB=6,AC=10,AD=8.求证: ABCD是矩形.
8.如示,在 ABCD中,EF∥BC,GH∥AB,则中的平行四边形有 ( )
A.7个 B.8个 C.9个 D.10个
9.已知:如在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形.
10.如,在矩形ABCD中,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以每秒3 cm的速度向点B移动,点Q以每秒2 cm的速度向点D移动,当点P到达点B时,两点均停止移动.是否存在某一时刻,使四边形PBCQ为正方形 若存在,求出该时刻;若不存在,请说明理由.
11.如①所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长分别为1和2,另一种纸片的两条直角边长都为2.②,③,④是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请用三种方法将中所给的四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,三种方法所拼得的平行四边形(非矩形)的周长互不相等,并把你所拼得的形分别画在②,③,④的方格纸上.
要求:(1)所画形各顶点必须与方格纸中的小正方形顶点重合;
(2)画时,要保留四块直角三角形纸片的拼接痕迹.
教 师 详 解 详 析
二 15.2 平行四边形和特殊的平行四边形
1.A 2.B 3.C
4.C 解: 有一组邻边相等且有一个角是直角的平行四边形是正方形,选项C符合题意.
5.(1)矩形 (2)ac 解: (1)根据三个角是直角的四边形是矩形可得搭出的木框(木框的宽度忽略不计)的形状是矩形;(2)用(1)中的四根木条重新组合,搭出(1)中形状的木框的最大面积是ac.
6.解:3个,略.
7.证明:∵四边形ABCD为平行四边形,
∴BC=AD=8.
∵AB2+BC2=100,AC2=100,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
则∠ABC=90°,
∴ ABCD是矩形.
8.C
9.证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵AD平分∠BAC,
∴∠EAD=∠FAD(角平分线的定义).
∵DE∥AC,
∴∠FAD=∠EDA(两直线平行,内错角相等),
∴∠EAD=∠EDA(等量代换),
∴AE=DE,
∴四边形AEDF是菱形.
10.解:不存在.理由:设存在某时刻t,使得四边形PBCQ是正方形,则BP=CQ,即16-3t=2t,解得t=,∴CQ=2t=≠6,即CQ≠CB,
∴四边形PBCQ是正方形不成立.
故不存在某一时刻,使四边形PBCQ为正方形.
11.解:如.
同课章节目录
