北京课改版数学八年级下册同步课时练习:15.4.1 第1课时 矩形的性质(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:15.4.1 第1课时 矩形的性质(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 252.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览


文档简介
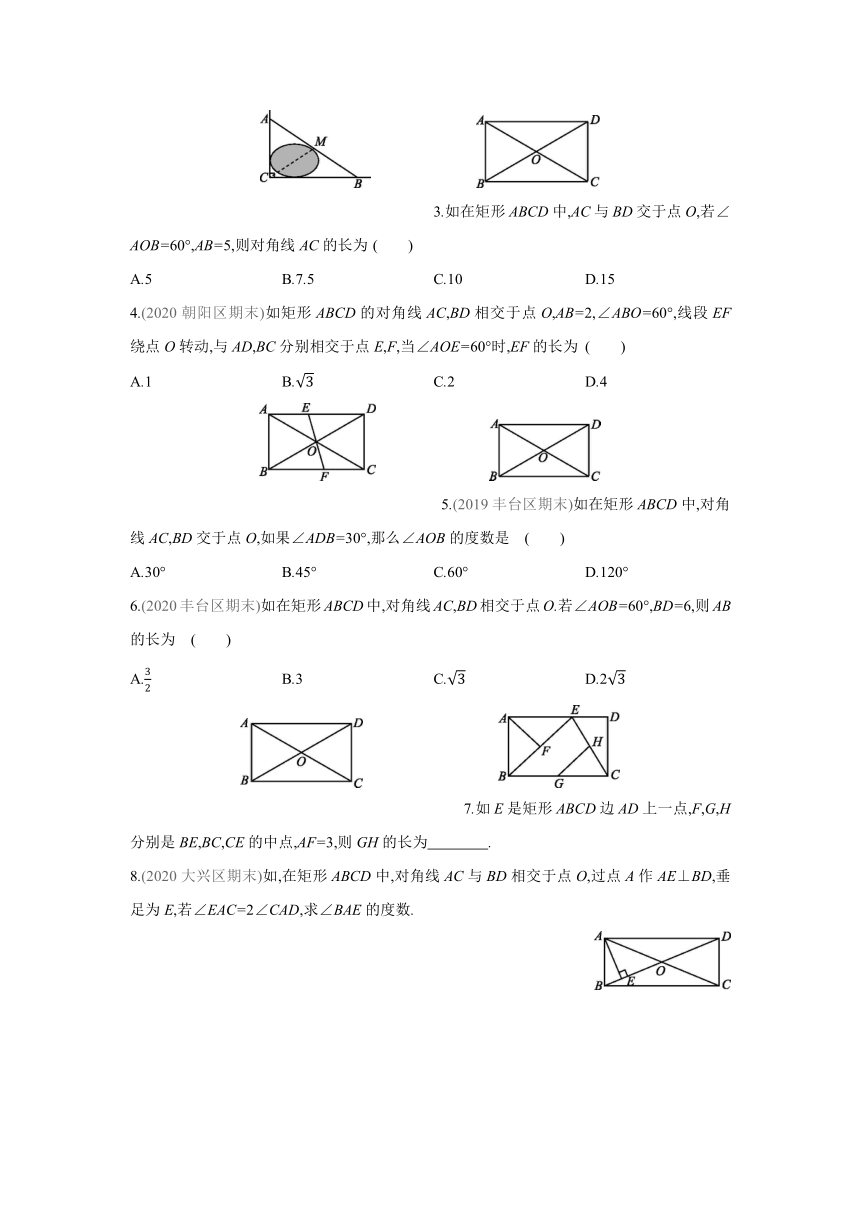
15.4 1.第1课时 矩形的性质
1.矩形性质定理1:矩形的四个角都是直角.
符号语言:如
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
2.矩形性质定理2:矩形的对角线相等.
符号语言:如
∵四边形ABCD是矩形,∴AC=BD.
3.矩形性质定理2的推论:
直角三角形斜边的中线等于斜边的一半.
符号语言:如
在Rt△ABC中,∠ACB=90°.
∵D是AB的中点,
∴DC=AB.
1.下列关于矩形的对角线,有甲、乙两种说法:
甲:矩形的对角线互相平分;
乙:矩形的对角线相等.
对于这两种说法,下列判断正确的是 ( )
A.甲、乙均正确
B.甲错误,乙正确
C.甲正确,乙错误
D.甲、乙均错误
2.如公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为
2.4 km,则M,C两点间的距离为 ( )
A.0.6 km B.1.2 km C.1.5 km D.2.4 km
3.如在矩形ABCD中,AC与BD交于点O,若∠AOB=60°,AB=5,则对角线AC的长为 ( )
A.5 B.7.5 C.10 D.15
4.(2020朝阳区期末)如矩形ABCD的对角线AC,BD相交于点O,AB=2,∠ABO=60°,线段EF绕点O转动,与AD,BC分别相交于点E,F,当∠AOE=60°时,EF的长为 ( )
A.1 B. C.2 D.4
5.(2019丰台区期末)如在矩形ABCD中,对角线AC,BD交于点O,如果∠ADB=30°,那么∠AOB的度数是 ( )
A.30° B.45° C.60° D.120°
6.(2020丰台区期末)如在矩形ABCD中,对角线AC,BD相交于点O.若∠AOB=60°,BD=6,则AB的长为 ( )
A. B.3 C. D.2
7.如E是矩形ABCD边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为 .
8.(2020大兴区期末)如,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为E,若∠EAC=2∠CAD,求∠BAE的度数.
9.(2020门头沟区期末)如,在矩形ABCD中,E是BC上的一点,DF=DC,DF⊥AE于点F.
(1)求证:AE=BC;
(2)如果AB=3,AF=4,求EC的长.
10.如,在矩形ABCD中,E,F分别是线段BC,AD的中点,AB=2,AD=4,动点P沿EC,CD,DF的路线由点E运动到点F,则△PAB的面积y是动点P运动的路径总长x的函数,这个函数的大致象可能是( )
11.(2019怀柔区期末)如,E为矩形ABCD的边BC上的一点,作DF⊥AE于点F,且满足DF=AB.有下列结论:①△DEF≌△DEC;②S△ABE=S△ADF;③AF=AB;④BE=AF.其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
12.按所示的方式摆放矩形纸片ABCD和矩形纸片ECGF,其中B,C,G三点共线,CE在CD上,连接AF,若M为AF的中点,连接DM,ME.
(1)DM与ME的数量关系是 ;
(2)请证明上面的结论.
13.如,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF的中点,求AM的最小值.
教 师 详 解 详 析
15.4 1.第1课时 矩形的性质
1.A 2.B 3.C 4.C 5.C 6.B
7.3 解: 在矩形ABCD中,∠BAD=90°.
又∵F为BE的中点,AF=3,∴BE=2AF=6.
∵G,H分别为BC,EC的中点,
∴GH=BE=3.
8.解:∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD,∴OA=OB=OC,
则∠OAD=∠ODA,∠OAB=∠OBA,
∴∠AOE=∠OAD+∠ODA=2∠OAD.
∵∠EAC=2∠CAD,∴∠OAE=∠AOE.
∵AE⊥BD,∴∠AEO=90°,
∴∠AOE=∠OAE=45°,
则∠OAB=∠OBA=(180°-45°)=67.5°,
∴∠BAE=∠OAB-∠OAE=22.5°.
9.解:(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AB=DC,AD=BC,AD∥BC,
∴∠AEB=∠DAF.
∵DF⊥AE,
∴∠AFD=90°,
∴∠AFD=∠B.
∵DF=DC,∴AB=DF,
∴△ABE≌△DFA,
则AE=AD,∴AE=BC.
(2)由(1),得△ABE≌△DFA,
∴BE=AF=4.
∵∠B=90°,
由勾股定理,得AE===5,
∴BC=5,
∴EC=BC-BE=5-4=1.
10.C 解: 根据题意,当点P由点E向点C运动时,△PAB的面积匀速增加;当点P由点C向点D运动时,△PAB的面积保持不变;当点P由点D向点F运动时,△PAB的面积匀速减小但不为0.故选C.
11.C 解: ∵四边形ABCD是矩形,
∴∠C=∠ABE=90°,AD∥BC,AB=CD.
又∵DF=AB,
∴DF=CD.
∵DF⊥AE,
∴∠DFA=∠DFE=90°.
在Rt△DEF和Rt△DEC中,DE=DE,DF=DC,
∴Rt△DEF≌Rt△DEC,①正确;
∵AD∥BC,
∴∠AEB=∠DAF.
又∵∠ABE=∠DFA,
∴△ABE≌△DFA,
∴S△ABE=S△DFA,
∴BE=AF,
∴②④正确,③不正确;正确的结论有3个.故选C.
12.解:(1)DM=ME
(2)证明:如所示,延长EM交AD于点H.
∵四边形ABCD和四边形ECGF是矩形,
∴AD∥EF,∴∠EFM=∠HAM.
又∵∠FME=∠AMH,FM=AM,
∴△FME≌△AMH,∴HM=ME.
在Rt△HDE中,∵HM=ME,
∴DM=HM=ME,
∴DM=ME.
13.解:连接AP,如.∵∠BAC=90°,AB=6,AC=8,
∴BC===10.
∵PE⊥AB,PF⊥AC,∠BAC=90°,∴四边形AFPE是矩形,
∴EF=AP,EF与AP互相平分.
∵M是EF的中点,∴点M在AP上且M为AP的中点,
∴AM=AP.
当AP⊥BC时,AP最短,同样AM也最短.
当AP⊥BC时,AP===4.8,∴当AM最短时,AM=AP=2.4.即AM的最小值为2.4.
1.矩形性质定理1:矩形的四个角都是直角.
符号语言:如
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
2.矩形性质定理2:矩形的对角线相等.
符号语言:如
∵四边形ABCD是矩形,∴AC=BD.
3.矩形性质定理2的推论:
直角三角形斜边的中线等于斜边的一半.
符号语言:如
在Rt△ABC中,∠ACB=90°.
∵D是AB的中点,
∴DC=AB.
1.下列关于矩形的对角线,有甲、乙两种说法:
甲:矩形的对角线互相平分;
乙:矩形的对角线相等.
对于这两种说法,下列判断正确的是 ( )
A.甲、乙均正确
B.甲错误,乙正确
C.甲正确,乙错误
D.甲、乙均错误
2.如公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为
2.4 km,则M,C两点间的距离为 ( )
A.0.6 km B.1.2 km C.1.5 km D.2.4 km
3.如在矩形ABCD中,AC与BD交于点O,若∠AOB=60°,AB=5,则对角线AC的长为 ( )
A.5 B.7.5 C.10 D.15
4.(2020朝阳区期末)如矩形ABCD的对角线AC,BD相交于点O,AB=2,∠ABO=60°,线段EF绕点O转动,与AD,BC分别相交于点E,F,当∠AOE=60°时,EF的长为 ( )
A.1 B. C.2 D.4
5.(2019丰台区期末)如在矩形ABCD中,对角线AC,BD交于点O,如果∠ADB=30°,那么∠AOB的度数是 ( )
A.30° B.45° C.60° D.120°
6.(2020丰台区期末)如在矩形ABCD中,对角线AC,BD相交于点O.若∠AOB=60°,BD=6,则AB的长为 ( )
A. B.3 C. D.2
7.如E是矩形ABCD边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为 .
8.(2020大兴区期末)如,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为E,若∠EAC=2∠CAD,求∠BAE的度数.
9.(2020门头沟区期末)如,在矩形ABCD中,E是BC上的一点,DF=DC,DF⊥AE于点F.
(1)求证:AE=BC;
(2)如果AB=3,AF=4,求EC的长.
10.如,在矩形ABCD中,E,F分别是线段BC,AD的中点,AB=2,AD=4,动点P沿EC,CD,DF的路线由点E运动到点F,则△PAB的面积y是动点P运动的路径总长x的函数,这个函数的大致象可能是( )
11.(2019怀柔区期末)如,E为矩形ABCD的边BC上的一点,作DF⊥AE于点F,且满足DF=AB.有下列结论:①△DEF≌△DEC;②S△ABE=S△ADF;③AF=AB;④BE=AF.其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
12.按所示的方式摆放矩形纸片ABCD和矩形纸片ECGF,其中B,C,G三点共线,CE在CD上,连接AF,若M为AF的中点,连接DM,ME.
(1)DM与ME的数量关系是 ;
(2)请证明上面的结论.
13.如,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF的中点,求AM的最小值.
教 师 详 解 详 析
15.4 1.第1课时 矩形的性质
1.A 2.B 3.C 4.C 5.C 6.B
7.3 解: 在矩形ABCD中,∠BAD=90°.
又∵F为BE的中点,AF=3,∴BE=2AF=6.
∵G,H分别为BC,EC的中点,
∴GH=BE=3.
8.解:∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD,∴OA=OB=OC,
则∠OAD=∠ODA,∠OAB=∠OBA,
∴∠AOE=∠OAD+∠ODA=2∠OAD.
∵∠EAC=2∠CAD,∴∠OAE=∠AOE.
∵AE⊥BD,∴∠AEO=90°,
∴∠AOE=∠OAE=45°,
则∠OAB=∠OBA=(180°-45°)=67.5°,
∴∠BAE=∠OAB-∠OAE=22.5°.
9.解:(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AB=DC,AD=BC,AD∥BC,
∴∠AEB=∠DAF.
∵DF⊥AE,
∴∠AFD=90°,
∴∠AFD=∠B.
∵DF=DC,∴AB=DF,
∴△ABE≌△DFA,
则AE=AD,∴AE=BC.
(2)由(1),得△ABE≌△DFA,
∴BE=AF=4.
∵∠B=90°,
由勾股定理,得AE===5,
∴BC=5,
∴EC=BC-BE=5-4=1.
10.C 解: 根据题意,当点P由点E向点C运动时,△PAB的面积匀速增加;当点P由点C向点D运动时,△PAB的面积保持不变;当点P由点D向点F运动时,△PAB的面积匀速减小但不为0.故选C.
11.C 解: ∵四边形ABCD是矩形,
∴∠C=∠ABE=90°,AD∥BC,AB=CD.
又∵DF=AB,
∴DF=CD.
∵DF⊥AE,
∴∠DFA=∠DFE=90°.
在Rt△DEF和Rt△DEC中,DE=DE,DF=DC,
∴Rt△DEF≌Rt△DEC,①正确;
∵AD∥BC,
∴∠AEB=∠DAF.
又∵∠ABE=∠DFA,
∴△ABE≌△DFA,
∴S△ABE=S△DFA,
∴BE=AF,
∴②④正确,③不正确;正确的结论有3个.故选C.
12.解:(1)DM=ME
(2)证明:如所示,延长EM交AD于点H.
∵四边形ABCD和四边形ECGF是矩形,
∴AD∥EF,∴∠EFM=∠HAM.
又∵∠FME=∠AMH,FM=AM,
∴△FME≌△AMH,∴HM=ME.
在Rt△HDE中,∵HM=ME,
∴DM=HM=ME,
∴DM=ME.
13.解:连接AP,如.∵∠BAC=90°,AB=6,AC=8,
∴BC===10.
∵PE⊥AB,PF⊥AC,∠BAC=90°,∴四边形AFPE是矩形,
∴EF=AP,EF与AP互相平分.
∵M是EF的中点,∴点M在AP上且M为AP的中点,
∴AM=AP.
当AP⊥BC时,AP最短,同样AM也最短.
当AP⊥BC时,AP===4.8,∴当AM最短时,AM=AP=2.4.即AM的最小值为2.4.
同课章节目录
