北京课改版数学八年级下册同步课时练习:15.4.2 第1课时 矩形的判定(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:15.4.2 第1课时 矩形的判定(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 173.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览


文档简介
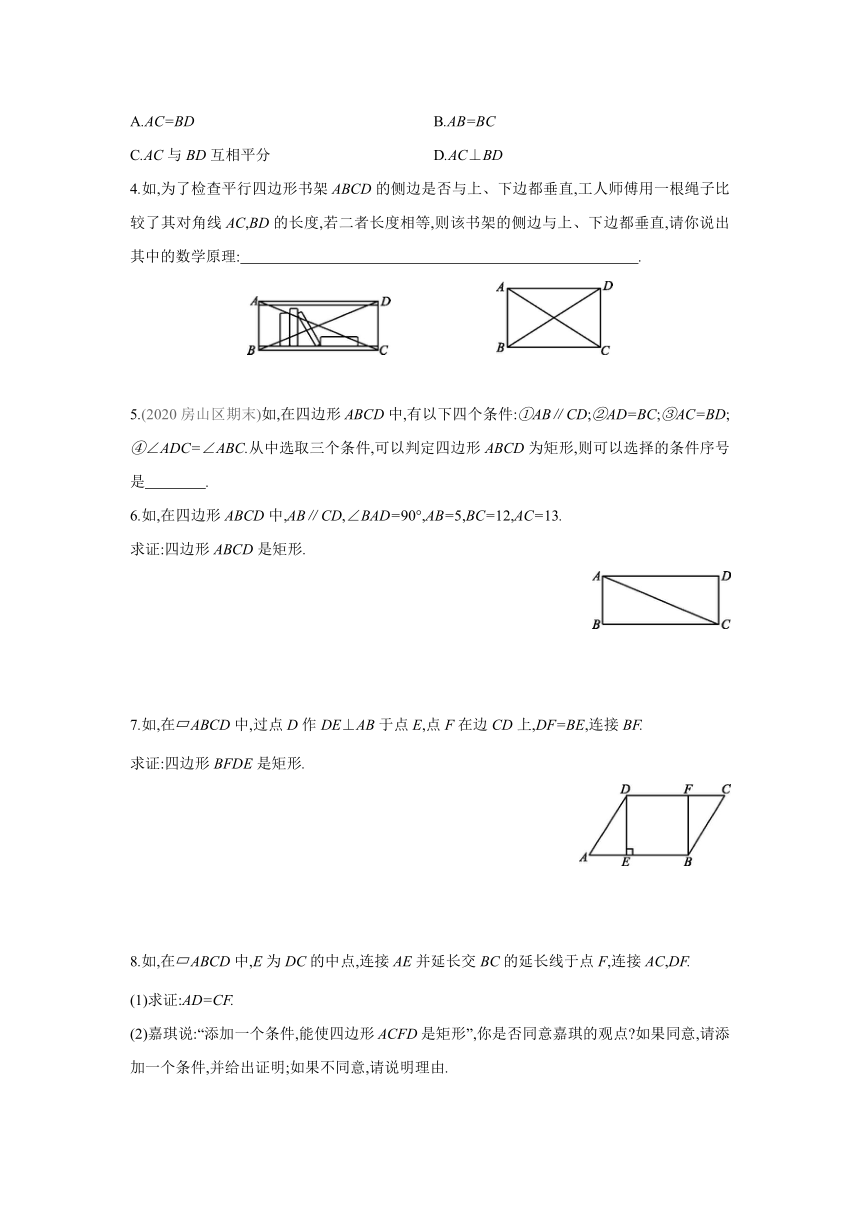
2.第1课时 矩形的判定
1.矩形判定定理1:对角线相等的平行四边形是矩形.
符号语言:如,在 ABCD中,
∵AC=BD,
∴ ABCD是矩形.
2.矩形判定定理2:有三个角是直角的四边形是矩形.
符号语言:
如,在四边形ABCD中,
∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
1.如,在 ABCD中,AC和BD相交于点O,则下面条件能判定 ABCD是矩形的是 ( )
A.AC=BD B.AC⊥BD C.AD=BC D.AB=AD
2.在数学活动课上,老师要求同学们判断一个四边形的门框是不是矩形,下面是某合作学习小组的四名同学拟定的方案,其中正确的是 ( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量一组对角线是否互相垂直
D.测量其内角是否有三个直角
3.已知在四边形ABCD中,∠ABC=90°,再补充一个条件使得ABCD为矩形,这个条件可以是 ( )
A.AC=BD B.AB=BC
C.AC与BD互相平分 D.AC⊥BD
4.如,为了检查平行四边形书架ABCD的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线AC,BD的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理: .
5.(2020房山区期末)如,在四边形ABCD中,有以下四个条件:①AB∥CD;②AD=BC;③AC=BD;④∠ADC=∠ABC.从中选取三个条件,可以判定四边形ABCD为矩形,则可以选择的条件序号是 .
6.如,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.
求证:四边形ABCD是矩形.
7.如,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接BF.
求证:四边形BFDE是矩形.
8.如,在 ABCD中,E为DC的中点,连接AE并延长交BC的延长线于点F,连接AC,DF.
(1)求证:AD=CF.
(2)嘉琪说:“添加一个条件,能使四边形ACFD是矩形”,你是否同意嘉琪的观点 如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.
9.下面是小东设计的“作矩形”的尺规作过程.
已知:在Rt△ABC中,∠ABC=90°.
求作:矩形ABCD.
作法:如,①作线段AC的垂直平分线交AC于点O;②连接BO并延长,在延长线上截取OD=OB;③连接AD,CD,则四边形ABCD即为所求作的矩形.根据小东设计的尺规作过程,解答下列各题.
(1)使用直尺和圆规,补全形(保留作痕迹);
(2)完成下面的证明(括号内填推理依据):
∵OA= ,OD=OB,
∴四边形ABCD是平行四边形( ).
∵∠ABC=90°,
∴四边形ABCD是矩形( ).
10.如,在 ABCD中,点E,F分别在边BC,AD上,BE=DF,∠AEC=90°.
(1)求证:四边形AECF是矩形;
(2)连接BF,若AB=4,∠ABC=60°,BF平分∠ABC,求AD的长.
11.如,已知在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与点A,B重合),过点P作PE⊥AC,PF⊥BC,垂足分别是E,F,连接EF,M为EF的中点.
(1)请判断四边形PECF的形状,并说明理由.
(2)随着点P在边AB上位置的改变,CM的长度是否也会改变 若不变,请你求出CM的长度;若有变化,请你求出CM长的变化范围.
教 师 详 解 详 析
2.第1课时 矩形的判定
1.A 2.D
3.C 解: ∵有一个角是直角的平行四边形是矩形,
∴只要四边形ABCD是平行四边形,即可判定四边形ABCD是矩形,
∴添加AC与BD互相平分.
4.对角线相等的平行四边形是矩形,矩形的四个角都是直角
5.①③④或②③④
6.证明:在四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°.
∵在△ABC中,AB=5,BC=12,AC=13,满足132=52+122,
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
7.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,即BE∥DF.
又∵DF=BE,
∴四边形BFDE是平行四边形.
∵DE⊥AB,∴∠DEB=90°,
∴四边形BFDE是矩形.
8.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠DAE=∠CFE,∠ADE=∠FCE.
∵E为DC的中点,∴ED=EC,
∴△ADE≌△FCE,∴AD=CF.
(2)同意.当DC=AF时,四边形ACFD是矩形.
证明:∵AD∥CF,AD=CF,
∴四边形ACFD是平行四边形.
又∵DC=AF,
∴四边形ACFD是矩形(所添加条件及证明不唯一).
9.解:(1)如.
(2)OC 对角线互相平分的四边形是平行四边形 有一个角是直角的平行四边形是矩形
10.解:(1)证明:∵四边形ABCD是平行四边形,∴BC=AD,BC∥AD.
又∵BE=DF,∴BC-BE=AD-DF,
即EC=AF.
又∵EC∥AF,
∴四边形AECF为平行四边形.
又∵∠AEC=90°,∴四边形AECF是矩形.
(2)在Rt△ABE中,∠AEB=90°,∠ABE=60°,AB=4,∴BE=2,AE=2.
∵四边形AECF是矩形,
∴FC⊥BC,FC=AE=2.
∵BF平分∠ABC,
∴∠FBC=∠ABC=30°.
在Rt△BCF中,∠FCB=90°,∠FBC=30°,FC=2,∴BC=6,∴AD=BC=6.
11.解:(1)四边形PECF是矩形.
理由:在△ABC中,AC=3,BC=4,AB=5,
∴AC2+BC2=32+42=52=AB2,
∴∠ACB=90°.
又∵PE⊥AC,PF⊥BC,
∴∠PEC=∠ACB=∠CFP=90°,
∴四边形PECF是矩形.
(2) CM的长度会改变.
连接PM,由(1)得四边形PECF是矩形,
∵M是EF的中点,
∴点C,M,P在同一直线上,且CM=PC.
过点C作CD⊥AB于点D,当PC=CD时,
PC的长最小,此时PC===2.4.
∵点P在斜边AB上(不与点A,B重合),
∴PC∴PC长的变化范围是2.4≤PC<4,
∴CM长的变化范围是1.2≤CM<2.
1.矩形判定定理1:对角线相等的平行四边形是矩形.
符号语言:如,在 ABCD中,
∵AC=BD,
∴ ABCD是矩形.
2.矩形判定定理2:有三个角是直角的四边形是矩形.
符号语言:
如,在四边形ABCD中,
∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
1.如,在 ABCD中,AC和BD相交于点O,则下面条件能判定 ABCD是矩形的是 ( )
A.AC=BD B.AC⊥BD C.AD=BC D.AB=AD
2.在数学活动课上,老师要求同学们判断一个四边形的门框是不是矩形,下面是某合作学习小组的四名同学拟定的方案,其中正确的是 ( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量一组对角线是否互相垂直
D.测量其内角是否有三个直角
3.已知在四边形ABCD中,∠ABC=90°,再补充一个条件使得ABCD为矩形,这个条件可以是 ( )
A.AC=BD B.AB=BC
C.AC与BD互相平分 D.AC⊥BD
4.如,为了检查平行四边形书架ABCD的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线AC,BD的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理: .
5.(2020房山区期末)如,在四边形ABCD中,有以下四个条件:①AB∥CD;②AD=BC;③AC=BD;④∠ADC=∠ABC.从中选取三个条件,可以判定四边形ABCD为矩形,则可以选择的条件序号是 .
6.如,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.
求证:四边形ABCD是矩形.
7.如,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接BF.
求证:四边形BFDE是矩形.
8.如,在 ABCD中,E为DC的中点,连接AE并延长交BC的延长线于点F,连接AC,DF.
(1)求证:AD=CF.
(2)嘉琪说:“添加一个条件,能使四边形ACFD是矩形”,你是否同意嘉琪的观点 如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.
9.下面是小东设计的“作矩形”的尺规作过程.
已知:在Rt△ABC中,∠ABC=90°.
求作:矩形ABCD.
作法:如,①作线段AC的垂直平分线交AC于点O;②连接BO并延长,在延长线上截取OD=OB;③连接AD,CD,则四边形ABCD即为所求作的矩形.根据小东设计的尺规作过程,解答下列各题.
(1)使用直尺和圆规,补全形(保留作痕迹);
(2)完成下面的证明(括号内填推理依据):
∵OA= ,OD=OB,
∴四边形ABCD是平行四边形( ).
∵∠ABC=90°,
∴四边形ABCD是矩形( ).
10.如,在 ABCD中,点E,F分别在边BC,AD上,BE=DF,∠AEC=90°.
(1)求证:四边形AECF是矩形;
(2)连接BF,若AB=4,∠ABC=60°,BF平分∠ABC,求AD的长.
11.如,已知在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与点A,B重合),过点P作PE⊥AC,PF⊥BC,垂足分别是E,F,连接EF,M为EF的中点.
(1)请判断四边形PECF的形状,并说明理由.
(2)随着点P在边AB上位置的改变,CM的长度是否也会改变 若不变,请你求出CM的长度;若有变化,请你求出CM长的变化范围.
教 师 详 解 详 析
2.第1课时 矩形的判定
1.A 2.D
3.C 解: ∵有一个角是直角的平行四边形是矩形,
∴只要四边形ABCD是平行四边形,即可判定四边形ABCD是矩形,
∴添加AC与BD互相平分.
4.对角线相等的平行四边形是矩形,矩形的四个角都是直角
5.①③④或②③④
6.证明:在四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°.
∵在△ABC中,AB=5,BC=12,AC=13,满足132=52+122,
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
7.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,即BE∥DF.
又∵DF=BE,
∴四边形BFDE是平行四边形.
∵DE⊥AB,∴∠DEB=90°,
∴四边形BFDE是矩形.
8.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠DAE=∠CFE,∠ADE=∠FCE.
∵E为DC的中点,∴ED=EC,
∴△ADE≌△FCE,∴AD=CF.
(2)同意.当DC=AF时,四边形ACFD是矩形.
证明:∵AD∥CF,AD=CF,
∴四边形ACFD是平行四边形.
又∵DC=AF,
∴四边形ACFD是矩形(所添加条件及证明不唯一).
9.解:(1)如.
(2)OC 对角线互相平分的四边形是平行四边形 有一个角是直角的平行四边形是矩形
10.解:(1)证明:∵四边形ABCD是平行四边形,∴BC=AD,BC∥AD.
又∵BE=DF,∴BC-BE=AD-DF,
即EC=AF.
又∵EC∥AF,
∴四边形AECF为平行四边形.
又∵∠AEC=90°,∴四边形AECF是矩形.
(2)在Rt△ABE中,∠AEB=90°,∠ABE=60°,AB=4,∴BE=2,AE=2.
∵四边形AECF是矩形,
∴FC⊥BC,FC=AE=2.
∵BF平分∠ABC,
∴∠FBC=∠ABC=30°.
在Rt△BCF中,∠FCB=90°,∠FBC=30°,FC=2,∴BC=6,∴AD=BC=6.
11.解:(1)四边形PECF是矩形.
理由:在△ABC中,AC=3,BC=4,AB=5,
∴AC2+BC2=32+42=52=AB2,
∴∠ACB=90°.
又∵PE⊥AC,PF⊥BC,
∴∠PEC=∠ACB=∠CFP=90°,
∴四边形PECF是矩形.
(2) CM的长度会改变.
连接PM,由(1)得四边形PECF是矩形,
∵M是EF的中点,
∴点C,M,P在同一直线上,且CM=PC.
过点C作CD⊥AB于点D,当PC=CD时,
PC的长最小,此时PC===2.4.
∵点P在斜边AB上(不与点A,B重合),
∴PC
∴CM长的变化范围是1.2≤CM<2.
同课章节目录
