北京课改版数学八年级下册同步课时练习:15.4.1 第3课时 正方形的性质(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:15.4.1 第3课时 正方形的性质(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 250.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
第3课时 正方形的性质
1.正方形边的性质:
正方形的四条边相等.
2.正方形角的性质:
正方形的四个角都是直角.
3.正方形对角线的性质:
(1)正方形的两条对角线相等.
(2)正方形的两条对角线互相垂直平分.
(3)正方形的每条对角线都平分一组对角.
4.正方形是轴对称形,对称轴有4条.
1.正方形是轴对称形,它的对称轴有 ( )
A.2条 B.4条 C.6条 D.8条
2.正方形具有而矩形不具有的性质是 ( )
A.对角相等 B.对角线互相平分 C.对角线相等 D.对角线互相垂直
3.正方形的一条对角线长为4,则这个正方形的面积是 ( )
A.8 B.4 C.8 D.16
4.如所示,以正方形ABCD中的AD边为一边向外作等边三角形ADE,则∠AEB的度数为 ( )
A.10° B.15° C.20° D.12.5°
5.如,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为 ( )
A.22.5° B.60° C.67.5° D.75°
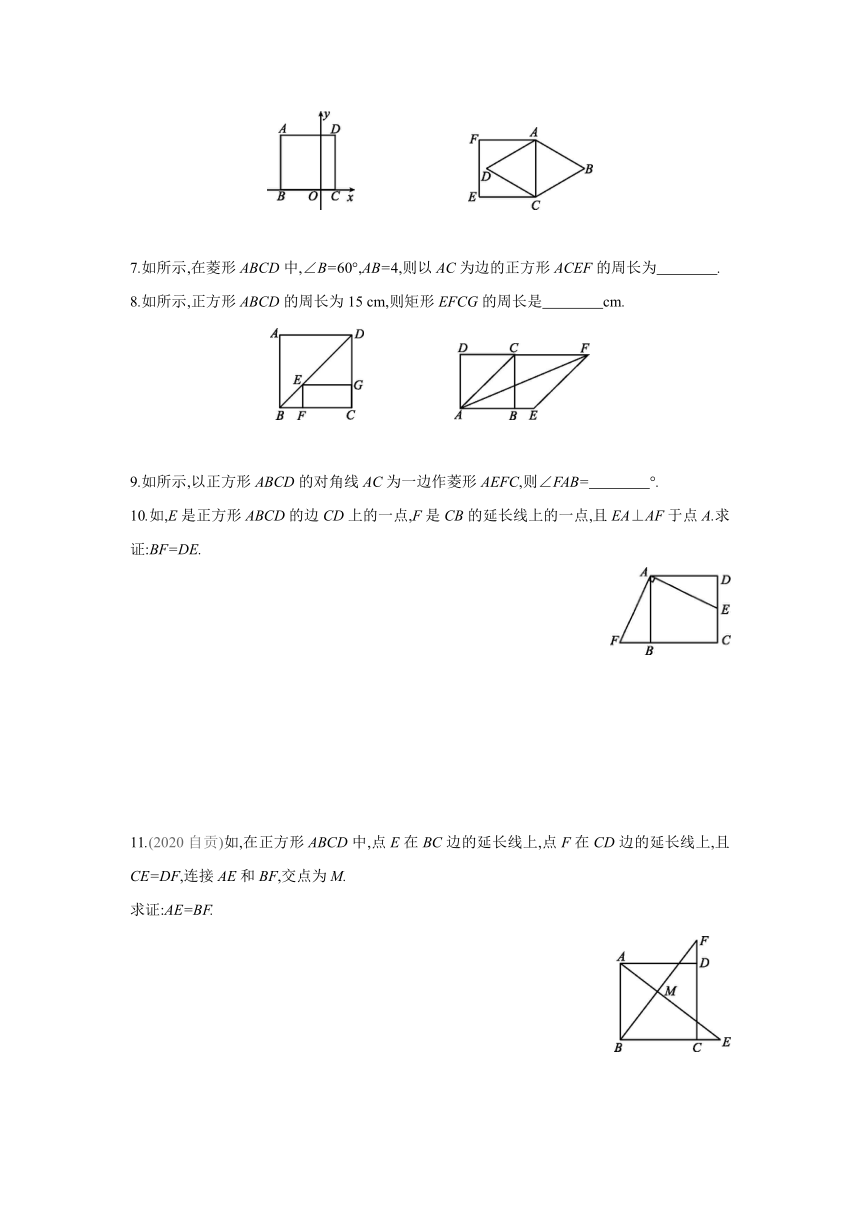
6.如所示,正方形ABCD的顶点B,C都在x轴上.若点D的坐标为(1,4),则点B的坐标是 .
7.如所示,在菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为 .
8.如所示,正方形ABCD的周长为15 cm,则矩形EFCG的周长是 cm.
9.如所示,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB= °.
10.如,E是正方形ABCD的边CD上的一点,F是CB的延长线上的一点,且EA⊥AF于点A.求证:BF=DE.
11.(2020自贡)如,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连接AE和BF,交点为M.
求证:AE=BF.
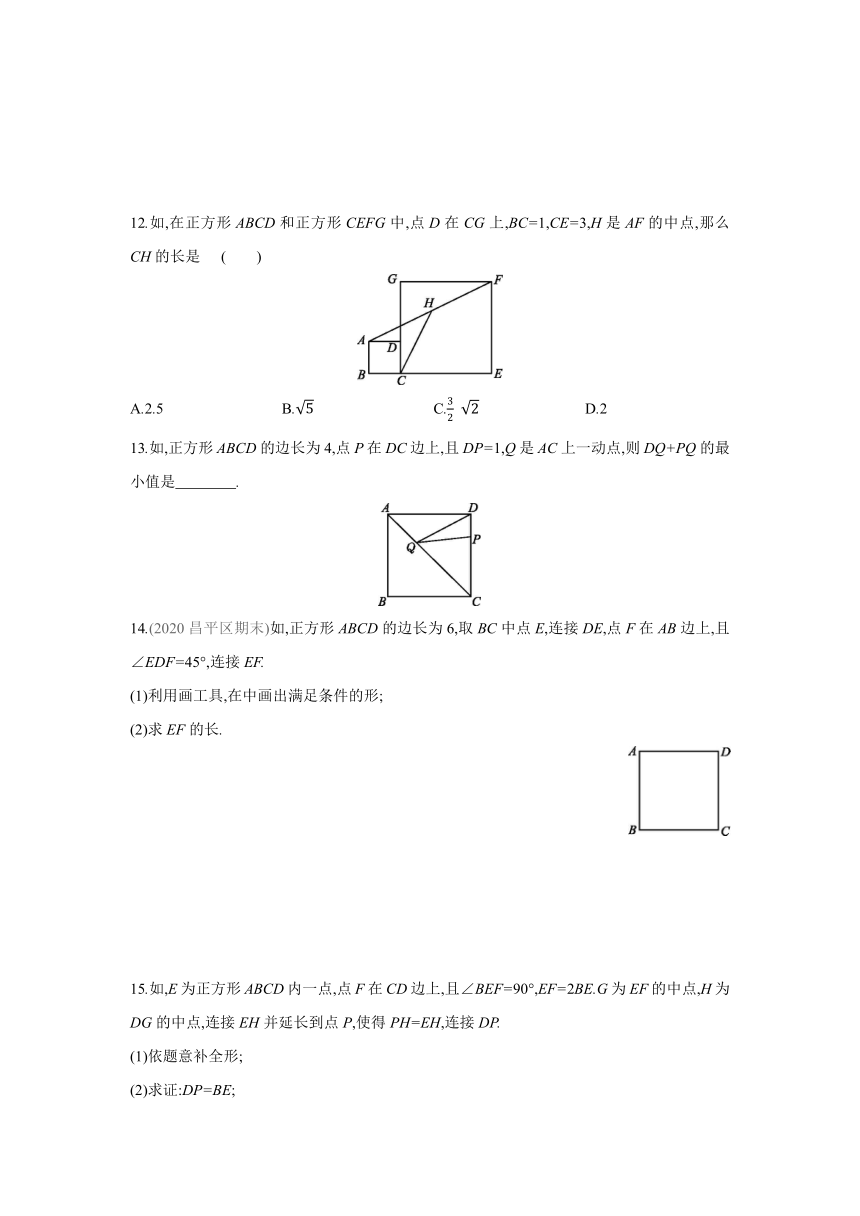
12.如,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
A.2.5 B. C. D.2
13.如,正方形ABCD的边长为4,点P在DC边上,且DP=1,Q是AC上一动点,则DQ+PQ的最小值是 .
14.(2020昌平区期末)如,正方形ABCD的边长为6,取BC中点E,连接DE,点F在AB边上,且∠EDF=45°,连接EF.
(1)利用画工具,在中画出满足条件的形;
(2)求EF的长.
15.如,E为正方形ABCD内一点,点F在CD边上,且∠BEF=90°,EF=2BE.G为EF的中点,H为DG的中点,连接EH并延长到点P,使得PH=EH,连接DP.
(1)依题意补全形;
(2)求证:DP=BE;
(3)连接EC,CP,猜想线段EC和CP的数量关系并证明.
教 师 详 解 详 析
第3课时 正方形的性质
1.B
2.D 解: 因为正方形的对角相等,对角线相等、垂直、且互相平分,矩形的对角相等,对角线相等,互相平分,所以正方形具有而矩形不具有的性质是对角线互相垂直.故选D.
3.A 解: ∵正方形的一条对角线长为4,
∴这个正方形的面积=×4×4=8.
4.B
5.C 解: ∵四边形ABCD是正方形,∴BC=CD,∠DBC=45°.
又∵BE=CD,∴BE=BC,∴∠BEC=∠BCE=(180°-45°)=67.5°.
6.(-3,0) 解: 根据正方形的性质,可知BC=DC=4.根据点D的坐标可知OC=1,所以OB=3,则点B的坐标为(-3,0).
7.16 8. 9.22.5
10.证明:∵四边形ABCD是正方形,∴∠BAD=∠ABF=∠ADE=90°,AB=AD,
∴∠EAD+∠BAE=90°.
∵EA⊥AF,∴∠FAB+∠BAE=90°,∴∠FAB=∠EAD,
∴△AFB≌△AED,∴BF=DE.
11.证明:∵四边形ABCD为正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°.
∵CE=DF,∴BC+CE=CD+DF,
即BE=CF.
∴△AEB≌△BFC(SAS),∴AE=BF.
12.B 解: 如,连接AC,CF.
∵在正方形ABCD和正方形CEFG中,BC=1,CE=3,
∴AC=,CF=3,∠ACD=∠GCF=45°,∴∠ACF=90°.
在Rt△ACF中,由勾股定理,得AF=2.
∵H是AF的中点,∴CH=AF=×2=.
13.5 解: 如,连接BP.
∵点B和点D关于直线AC对称,
∴BQ=DQ,
则BP的长就是DQ+PQ的最小值.
∵正方形ABCD的边长是4,DP=1,
∴CP=3,
∴BP==5,
∴DQ+PQ的最小值是5.
14.解:(1)如①.
(2)如②,在BA的延长线上截取AG=CE,连接DG.
∵四边形ABCD是正方形,
∴AD=CD=BC=AB=6,
∠DAF=∠ABC=∠ADC=∠BCD=90°,
∴∠GAD=90°,
∴△AGD≌△CED.
则∠GDA=∠EDC,GD=ED.
∵∠FDE=45°,∴∠ADF+∠EDC=45°,
∴∠ADF+∠GDA=45°,
∴∠GDF=∠EDF.
又∵DF=DF,
∴△GDF≌△EDF,∴GF=EF.
设AF=x,则FB=6-x.
∵E为BC的中点,∴BE=EC=3,∴AG=3,
∴FG=EF=3+x.
在Rt△BEF中,∠ABC=90°,由勾股定理,得BF2+BE2=EF2,
即(6-x)2+32=(3+x)2,
∴x=2,∴AF=2,
∴EF=3+x=3+2=5.
15.解:(1)依题意补全形如.
(2)证明:∵H为线段DG的中点,∴DH=GH.
又∵EH=PH,∠EHG=∠PHD,
∴△PDH≌△EGH,∴DP=EG.
∵G为EF的中点,∴EF=2EG.
∵EF=2BE,∴DP=EG=BE.
(3)EC=CP.
证明:如.由(2)可知△PDH≌△EGH,
∴∠HEG=∠HPD,
∴DP∥EF,∴∠PDC=∠DFE.
∵∠BEF=∠BCD=90°,
∴∠EBC+∠EFC=180°.
又∵∠DFE+∠EFC=180°,
∴∠EBC=∠DFE=∠PDC.
又∵BC=DC,BE=DP,∴△EBC≌△PDC,
∴EC=CP.
1.正方形边的性质:
正方形的四条边相等.
2.正方形角的性质:
正方形的四个角都是直角.
3.正方形对角线的性质:
(1)正方形的两条对角线相等.
(2)正方形的两条对角线互相垂直平分.
(3)正方形的每条对角线都平分一组对角.
4.正方形是轴对称形,对称轴有4条.
1.正方形是轴对称形,它的对称轴有 ( )
A.2条 B.4条 C.6条 D.8条
2.正方形具有而矩形不具有的性质是 ( )
A.对角相等 B.对角线互相平分 C.对角线相等 D.对角线互相垂直
3.正方形的一条对角线长为4,则这个正方形的面积是 ( )
A.8 B.4 C.8 D.16
4.如所示,以正方形ABCD中的AD边为一边向外作等边三角形ADE,则∠AEB的度数为 ( )
A.10° B.15° C.20° D.12.5°
5.如,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为 ( )
A.22.5° B.60° C.67.5° D.75°
6.如所示,正方形ABCD的顶点B,C都在x轴上.若点D的坐标为(1,4),则点B的坐标是 .
7.如所示,在菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为 .
8.如所示,正方形ABCD的周长为15 cm,则矩形EFCG的周长是 cm.
9.如所示,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB= °.
10.如,E是正方形ABCD的边CD上的一点,F是CB的延长线上的一点,且EA⊥AF于点A.求证:BF=DE.
11.(2020自贡)如,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连接AE和BF,交点为M.
求证:AE=BF.
12.如,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
A.2.5 B. C. D.2
13.如,正方形ABCD的边长为4,点P在DC边上,且DP=1,Q是AC上一动点,则DQ+PQ的最小值是 .
14.(2020昌平区期末)如,正方形ABCD的边长为6,取BC中点E,连接DE,点F在AB边上,且∠EDF=45°,连接EF.
(1)利用画工具,在中画出满足条件的形;
(2)求EF的长.
15.如,E为正方形ABCD内一点,点F在CD边上,且∠BEF=90°,EF=2BE.G为EF的中点,H为DG的中点,连接EH并延长到点P,使得PH=EH,连接DP.
(1)依题意补全形;
(2)求证:DP=BE;
(3)连接EC,CP,猜想线段EC和CP的数量关系并证明.
教 师 详 解 详 析
第3课时 正方形的性质
1.B
2.D 解: 因为正方形的对角相等,对角线相等、垂直、且互相平分,矩形的对角相等,对角线相等,互相平分,所以正方形具有而矩形不具有的性质是对角线互相垂直.故选D.
3.A 解: ∵正方形的一条对角线长为4,
∴这个正方形的面积=×4×4=8.
4.B
5.C 解: ∵四边形ABCD是正方形,∴BC=CD,∠DBC=45°.
又∵BE=CD,∴BE=BC,∴∠BEC=∠BCE=(180°-45°)=67.5°.
6.(-3,0) 解: 根据正方形的性质,可知BC=DC=4.根据点D的坐标可知OC=1,所以OB=3,则点B的坐标为(-3,0).
7.16 8. 9.22.5
10.证明:∵四边形ABCD是正方形,∴∠BAD=∠ABF=∠ADE=90°,AB=AD,
∴∠EAD+∠BAE=90°.
∵EA⊥AF,∴∠FAB+∠BAE=90°,∴∠FAB=∠EAD,
∴△AFB≌△AED,∴BF=DE.
11.证明:∵四边形ABCD为正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°.
∵CE=DF,∴BC+CE=CD+DF,
即BE=CF.
∴△AEB≌△BFC(SAS),∴AE=BF.
12.B 解: 如,连接AC,CF.
∵在正方形ABCD和正方形CEFG中,BC=1,CE=3,
∴AC=,CF=3,∠ACD=∠GCF=45°,∴∠ACF=90°.
在Rt△ACF中,由勾股定理,得AF=2.
∵H是AF的中点,∴CH=AF=×2=.
13.5 解: 如,连接BP.
∵点B和点D关于直线AC对称,
∴BQ=DQ,
则BP的长就是DQ+PQ的最小值.
∵正方形ABCD的边长是4,DP=1,
∴CP=3,
∴BP==5,
∴DQ+PQ的最小值是5.
14.解:(1)如①.
(2)如②,在BA的延长线上截取AG=CE,连接DG.
∵四边形ABCD是正方形,
∴AD=CD=BC=AB=6,
∠DAF=∠ABC=∠ADC=∠BCD=90°,
∴∠GAD=90°,
∴△AGD≌△CED.
则∠GDA=∠EDC,GD=ED.
∵∠FDE=45°,∴∠ADF+∠EDC=45°,
∴∠ADF+∠GDA=45°,
∴∠GDF=∠EDF.
又∵DF=DF,
∴△GDF≌△EDF,∴GF=EF.
设AF=x,则FB=6-x.
∵E为BC的中点,∴BE=EC=3,∴AG=3,
∴FG=EF=3+x.
在Rt△BEF中,∠ABC=90°,由勾股定理,得BF2+BE2=EF2,
即(6-x)2+32=(3+x)2,
∴x=2,∴AF=2,
∴EF=3+x=3+2=5.
15.解:(1)依题意补全形如.
(2)证明:∵H为线段DG的中点,∴DH=GH.
又∵EH=PH,∠EHG=∠PHD,
∴△PDH≌△EGH,∴DP=EG.
∵G为EF的中点,∴EF=2EG.
∵EF=2BE,∴DP=EG=BE.
(3)EC=CP.
证明:如.由(2)可知△PDH≌△EGH,
∴∠HEG=∠HPD,
∴DP∥EF,∴∠PDC=∠DFE.
∵∠BEF=∠BCD=90°,
∴∠EBC+∠EFC=180°.
又∵∠DFE+∠EFC=180°,
∴∠EBC=∠DFE=∠PDC.
又∵BC=DC,BE=DP,∴△EBC≌△PDC,
∴EC=CP.
同课章节目录
