北京课改版数学八年级下册同步课时练习:15.4.2 第3课时 正方形的判定(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:15.4.2 第3课时 正方形的判定(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览


文档简介
第3课时 正方形的判定
正方形的判定方法:
1.有一个角是直角的菱形是正方形.
2.对角线相等的菱形是正方形.
3.对角线互相垂直的矩形是正方形.
4.有一组邻边相等的矩形是正方形.
5.有一组邻边相等且有一个角是直角的平行四边形是正方形.
6.对角线互相垂直平分且相等的四边形是正方形.
1.要使矩形ABCD为正方形,需要添加的条件是 ( )
A.AB=BC B.AD=BC
C.AB=CD D.AC=BD
2.如,在菱形ABCD中,对角线AC,BD交于点O,添加下列一个条件,能使菱形ABCD成为正方形的是 ( )
A.BD=AB B.AC=AD
C.∠ABC=90° D.OD=AC
3.如果要证明 ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明 ( )
A.AC与BD互相垂直平分 B.∠A=∠B且AC=BD
C.AB=AD且AC=BD D.AB=AD且AC⊥BD
4.在四边形ABCD中,对角线AC,BD交于点O,下列条件中,能判定四边形ABCD为正方形的是( )
A.OA=OB=OC=OD,AB=CD B.OA=OC,OB=OD,AC⊥BD
C.OA=OB=OC=OD,AC⊥BD D.OA=OC,OB=OD,AB=BC
5.(2021河南模拟)如,正方形ABCD的边长为4,点M,N在对角线AC上(可与点A,C重合),MN=2,点P,Q在正方形的边上.下面四个结论中,
①存在无数个四边形PMQN是平行四边形;②存在无数个四边形PMQN是菱形;
③存在无数个四边形PMQN是矩形;
④至少存在一个四边形PMQN是正方形.
所有正确结论的序号是 .
6.(2020通州区模拟)如,已知线段AB,直线l垂直平分AB且交AB于点O,以点O为圆心,AO长为半径作弧,交直线l于C,D两点,分别连接AC,AD,BC,BD.
(1)根据题意,补全形;
(2)求证:四边形ACBD为正方形.
7.如,在Rt△ABC中,∠C=90°,∠CAB和∠CBA的平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F.
求证:(1)DE=DF;
(2)四边形CFDE是正方形.
8.(2019北京)在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,有下面四个结论:
①存在无数个四边形MNPQ是平行四边形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MNPQ是正方形.
其中正确结论的序号是 .
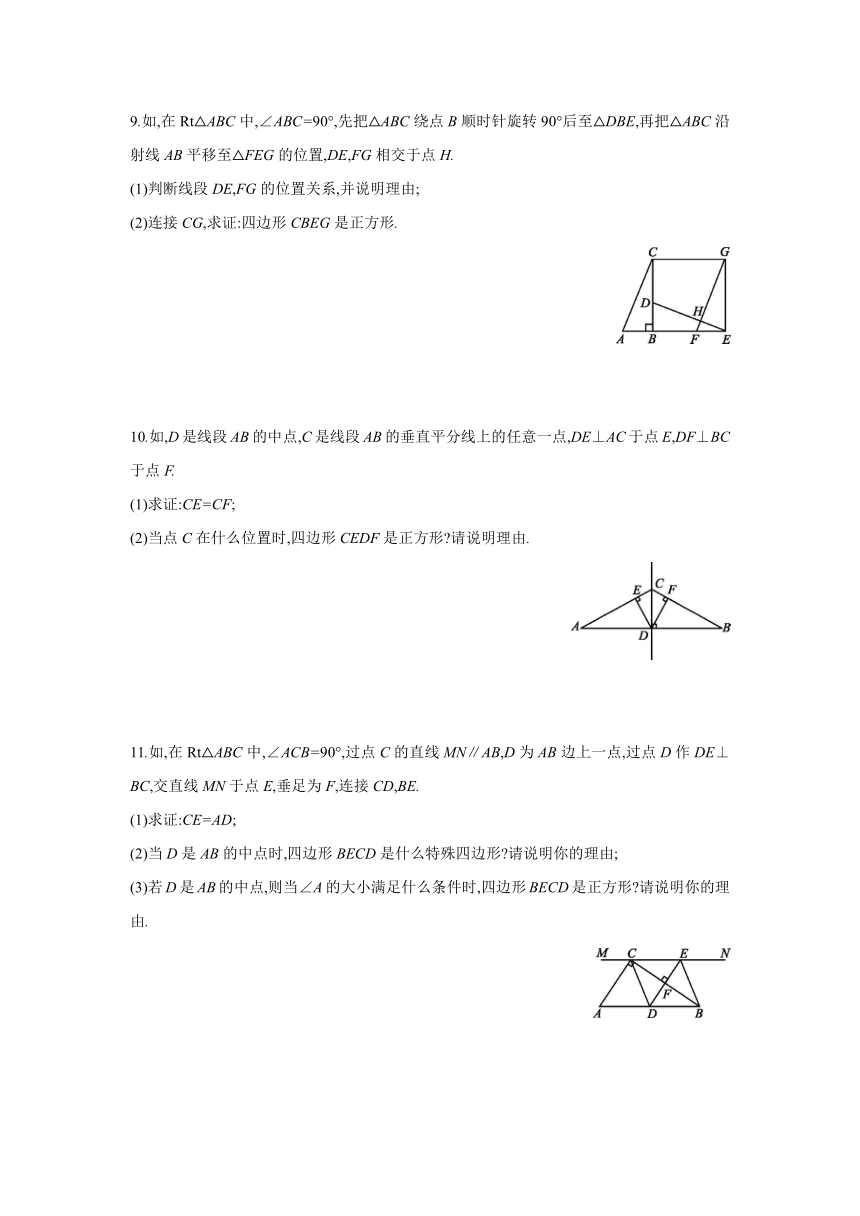
9.如,在Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG的位置,DE,FG相交于点H.
(1)判断线段DE,FG的位置关系,并说明理由;
(2)连接CG,求证:四边形CBEG是正方形.
10.如,D是线段AB的中点,C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)当点C在什么位置时,四边形CEDF是正方形 请说明理由.
11.如,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D是AB的中点时,四边形BECD是什么特殊四边形 请说明你的理由;
(3)若D是AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形 请说明你的理由.
教 师 详 解 详 析
第3课时 正方形的判定
1.A 2.C 3.C
4.C 解: 由OA=OB=OC=OD可得四边形ABCD是矩形,再由AC⊥BD,可得四边形ABCD是正方形.
5.①②④ 解: 作线段MN的垂直平分线交AD于点P,交AB于点Q.
∵PQ垂直平分线段MN,∴PM=PN,QM=QN.
∵四边形ABCD是正方形,∴∠PAN=∠QAN=45°,
∴∠APQ=∠AQP=45°,∴AP=AQ,∴AC垂直平分线段PQ,
∴MP=MQ,∴MP=NP=MQ=NQ,∴四边形PMQN是菱形.
在MN运动的过程中,这样的菱形有无数个,当点M与点A重合或点N与点C重合时,四边形PMQN是正方形,∴①②④正确.故答案为①②④.
6.解:(1)如所示.
(2)证明:由作可知OA=OC=OD.
又∵直线l垂直平分AB,
∴OA=OC=OD=OB,且AB,CD互相垂直,
∴AB=CD,
∴四边形ACBD为正方形.
7.证明:(1)过点D作DG⊥AB于点G.
∵AD平分∠CAB,DF⊥AC,DG⊥AB,
∴DF=DG.
同理可得DE=DG,
∴DE=DF.
(2)∵∠C=∠CED=∠CFD=90°,
∴四边形CFDE是矩形.
又∵DE=DF,
∴四边形CFDE是正方形.
8.①②③
9.解:(1)DE⊥FG.理由如下:
由题意,得∠A=∠BDE=∠EFG,
∠ABC=∠DBE=90°,
∴∠BDE+∠BED=90°,
∴∠EFG+∠BED=90°,∴∠FHE=90°,
即DE⊥FG.
(2)证明:∵△ABC沿射线AB平移至△FEG的位置,
∴CB∥GE,CB=GE,∠ABC=∠FEG=90°,
∴四边形CBEG是矩形.
又∵BC=BE,∴四边形CBEG是正方形.
10.解:(1)证明:∵CD垂直平分线段AB,
∴AC=BC.
又∵CD⊥AB,∴∠ACD=∠BCD.
∵DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°.
又∵CD=CD,∴△DEC≌△DFC,
∴CE=CF.
(2)当CD=AB时,四边形CEDF是正方形.理由如下:
∵CD⊥AB,
∴∠CDB=90°.
∵CD=AB,D是AB的中点,
∴CD=BD,
∴∠B=∠DCB=∠ACD=45°,
∴∠ACB=90°.
又∵∠CED=∠CFD=90°,
∴四边形CEDF是矩形.
又∵CE=CF,∴四边形CEDF是正方形.
11.解:(1)证明:∵DE⊥BC,
∴∠DFB=90°.
又∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE.
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD.
(2)四边形BECD是菱形.
理由:∵D是AB的中点,
∴AD=BD.
∵CE=AD,
∴BD=CE.
又∵BD∥CE,
∴四边形BECD是平行四边形.
又∵DE⊥BC,
∴四边形BECD是菱形.
(3)当∠A=45°时,四边形BECD是正方形.
理由:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC.
又∵D是AB的中点,
∴CD⊥AB,
∴∠CDB=90°.
又由(2)知四边形BECD是菱形,
∴四边形BECD是正方形.
正方形的判定方法:
1.有一个角是直角的菱形是正方形.
2.对角线相等的菱形是正方形.
3.对角线互相垂直的矩形是正方形.
4.有一组邻边相等的矩形是正方形.
5.有一组邻边相等且有一个角是直角的平行四边形是正方形.
6.对角线互相垂直平分且相等的四边形是正方形.
1.要使矩形ABCD为正方形,需要添加的条件是 ( )
A.AB=BC B.AD=BC
C.AB=CD D.AC=BD
2.如,在菱形ABCD中,对角线AC,BD交于点O,添加下列一个条件,能使菱形ABCD成为正方形的是 ( )
A.BD=AB B.AC=AD
C.∠ABC=90° D.OD=AC
3.如果要证明 ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明 ( )
A.AC与BD互相垂直平分 B.∠A=∠B且AC=BD
C.AB=AD且AC=BD D.AB=AD且AC⊥BD
4.在四边形ABCD中,对角线AC,BD交于点O,下列条件中,能判定四边形ABCD为正方形的是( )
A.OA=OB=OC=OD,AB=CD B.OA=OC,OB=OD,AC⊥BD
C.OA=OB=OC=OD,AC⊥BD D.OA=OC,OB=OD,AB=BC
5.(2021河南模拟)如,正方形ABCD的边长为4,点M,N在对角线AC上(可与点A,C重合),MN=2,点P,Q在正方形的边上.下面四个结论中,
①存在无数个四边形PMQN是平行四边形;②存在无数个四边形PMQN是菱形;
③存在无数个四边形PMQN是矩形;
④至少存在一个四边形PMQN是正方形.
所有正确结论的序号是 .
6.(2020通州区模拟)如,已知线段AB,直线l垂直平分AB且交AB于点O,以点O为圆心,AO长为半径作弧,交直线l于C,D两点,分别连接AC,AD,BC,BD.
(1)根据题意,补全形;
(2)求证:四边形ACBD为正方形.
7.如,在Rt△ABC中,∠C=90°,∠CAB和∠CBA的平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F.
求证:(1)DE=DF;
(2)四边形CFDE是正方形.
8.(2019北京)在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,有下面四个结论:
①存在无数个四边形MNPQ是平行四边形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MNPQ是正方形.
其中正确结论的序号是 .
9.如,在Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG的位置,DE,FG相交于点H.
(1)判断线段DE,FG的位置关系,并说明理由;
(2)连接CG,求证:四边形CBEG是正方形.
10.如,D是线段AB的中点,C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)当点C在什么位置时,四边形CEDF是正方形 请说明理由.
11.如,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D是AB的中点时,四边形BECD是什么特殊四边形 请说明你的理由;
(3)若D是AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形 请说明你的理由.
教 师 详 解 详 析
第3课时 正方形的判定
1.A 2.C 3.C
4.C 解: 由OA=OB=OC=OD可得四边形ABCD是矩形,再由AC⊥BD,可得四边形ABCD是正方形.
5.①②④ 解: 作线段MN的垂直平分线交AD于点P,交AB于点Q.
∵PQ垂直平分线段MN,∴PM=PN,QM=QN.
∵四边形ABCD是正方形,∴∠PAN=∠QAN=45°,
∴∠APQ=∠AQP=45°,∴AP=AQ,∴AC垂直平分线段PQ,
∴MP=MQ,∴MP=NP=MQ=NQ,∴四边形PMQN是菱形.
在MN运动的过程中,这样的菱形有无数个,当点M与点A重合或点N与点C重合时,四边形PMQN是正方形,∴①②④正确.故答案为①②④.
6.解:(1)如所示.
(2)证明:由作可知OA=OC=OD.
又∵直线l垂直平分AB,
∴OA=OC=OD=OB,且AB,CD互相垂直,
∴AB=CD,
∴四边形ACBD为正方形.
7.证明:(1)过点D作DG⊥AB于点G.
∵AD平分∠CAB,DF⊥AC,DG⊥AB,
∴DF=DG.
同理可得DE=DG,
∴DE=DF.
(2)∵∠C=∠CED=∠CFD=90°,
∴四边形CFDE是矩形.
又∵DE=DF,
∴四边形CFDE是正方形.
8.①②③
9.解:(1)DE⊥FG.理由如下:
由题意,得∠A=∠BDE=∠EFG,
∠ABC=∠DBE=90°,
∴∠BDE+∠BED=90°,
∴∠EFG+∠BED=90°,∴∠FHE=90°,
即DE⊥FG.
(2)证明:∵△ABC沿射线AB平移至△FEG的位置,
∴CB∥GE,CB=GE,∠ABC=∠FEG=90°,
∴四边形CBEG是矩形.
又∵BC=BE,∴四边形CBEG是正方形.
10.解:(1)证明:∵CD垂直平分线段AB,
∴AC=BC.
又∵CD⊥AB,∴∠ACD=∠BCD.
∵DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°.
又∵CD=CD,∴△DEC≌△DFC,
∴CE=CF.
(2)当CD=AB时,四边形CEDF是正方形.理由如下:
∵CD⊥AB,
∴∠CDB=90°.
∵CD=AB,D是AB的中点,
∴CD=BD,
∴∠B=∠DCB=∠ACD=45°,
∴∠ACB=90°.
又∵∠CED=∠CFD=90°,
∴四边形CEDF是矩形.
又∵CE=CF,∴四边形CEDF是正方形.
11.解:(1)证明:∵DE⊥BC,
∴∠DFB=90°.
又∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE.
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD.
(2)四边形BECD是菱形.
理由:∵D是AB的中点,
∴AD=BD.
∵CE=AD,
∴BD=CE.
又∵BD∥CE,
∴四边形BECD是平行四边形.
又∵DE⊥BC,
∴四边形BECD是菱形.
(3)当∠A=45°时,四边形BECD是正方形.
理由:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC.
又∵D是AB的中点,
∴CD⊥AB,
∴∠CDB=90°.
又由(2)知四边形BECD是菱形,
∴四边形BECD是正方形.
同课章节目录
