北京课改版数学八年级下册同步课时练习:17.1 方差 17.2用科学计算器计算方差(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:17.1 方差 17.2用科学计算器计算方差(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 10:35:06 | ||
图片预览


文档简介
一 17.1 方差 17.2 用科学计算器计算方差
1.方差的定义:如果用x1,x2,…,xn表示一组数据,用表示这组数据的平均数,那么每个数据与平均数的差的平方数的平均值叫这组数据的方差.方差用s2来表示.
2.方差的计算公式:
s2=[(x1-)2+(x2-)2+…+(xn-)2].
3.方差的意义:方差描述了一组数据波动的大小,方差的值越小,数据波动越小、越整齐.
归纳:(1)研究数据的离散程度可用方差.
(2)衡量一组数据的波动大小可用方差.
(3)常用方差比较平均数相同或接近的两组数据波动的大小.
(4)方差大,数据波动大;方差小,数据波动小.
1.(2020门头沟区期末)方差表示一组数据的 ( )
A.平均水平 B.数据个数
C.最大值或最小值 D.波动大小
2.甲、乙两人在相同情况下各射靶10次,两人命中环数的平均数均为7,方差=3,=1.2,则射击成绩较稳定的是 ( )
A.甲 B.乙
C.甲、乙一样 D.不能确定
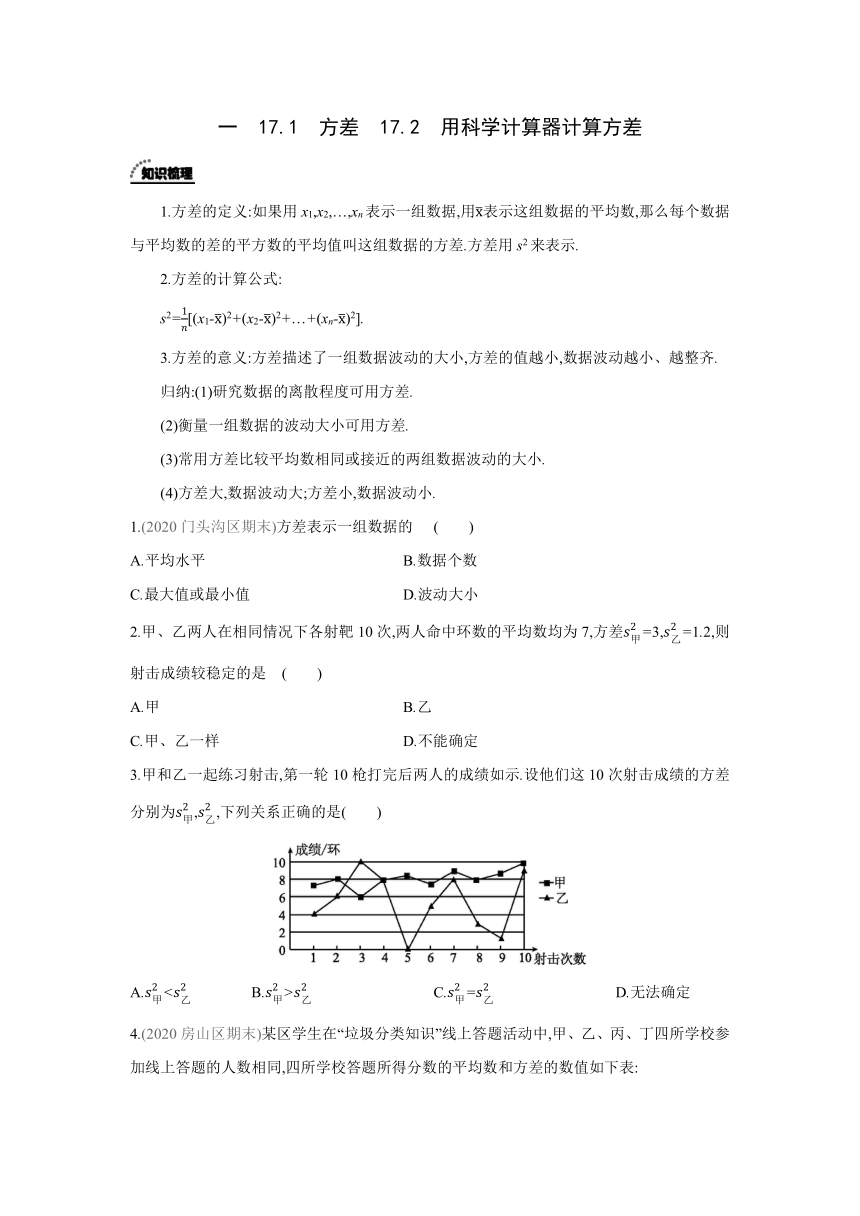
3.甲和乙一起练习射击,第一轮10枪打完后两人的成绩如示.设他们这10次射击成绩的方差分别为,,下列关系正确的是( )
A.< B.> C.= D.无法确定
4.(2020房山区期末)某区学生在“垃圾分类知识”线上答题活动中,甲、乙、丙、丁四所学校参加线上答题的人数相同,四所学校答题所得分数的平均数和方差的数值如下表:
学校 甲 乙 丙 丁
平均数(分) 87 87 87 87
方差 0.027 0.043 0.036 0.029
则这四所学校成绩发挥最稳定的是 ( )
A.甲 B.乙 C.丙 D.丁
5.已知样本数据2,4,2,5,2,下列说法不正确的是 ( )
A.平均数是3 B.中位数是2
C.方差是2 D.众数是2
6.一组数据-2,-1,0,x,1的平均数是0,则x= ,方差s2= .
7.为了满足不同顾客对保温时效的需要,保温杯生产厂家研发了甲、乙两款保温杯.现从甲、乙两款中各随机抽取了5个保温杯,测得保温时效(单位:h)如下表:
甲组 11 12 13 14 15
乙组 x 6 7 5 8
如果甲、乙两款保温杯保温时效的方差是相等的,那么x= .
8.甲、乙两台机床同时生产直径为10 mm的零件,为了检验产品质量,质检员从两台机床生产的产品中各抽出4件进行测量,结果(单位:mm)如下:
甲机床 10 9.8 10 10.2
乙机床 10.1 10 9.9 10
请你通过计算判断哪台机床生产的零件的质量更符合要求
9.一组数据0,-1,6,1,x的众数为-1,则这组数据的方差是 ( )
A.2 B. C. D.
10.如果一组数据x1,x2,…,xn的方差是3,那么另一组数据x1+5,x2+5,…,xn+5的方差是 ( )
A.3 B.8 C.9 D.14
11.若样本数据1,2,3,x的平均数为5,样本数据1,2,3,x,y的平均数为6,则样本数据1,2,3,x,y的方差是 .
12.(2021海淀区二模)品味诗词之美,传承中华文明,央视节目《中国诗词大会》备受大众欢迎.节目规则如下:由100位诗词爱好者组成的百人团与挑战者共同答题,每位挑战者最多可答五轮题.每轮比赛答题时,若挑战者答对,则百人团答错的人数即为选手该轮得分;若挑战者答错,则该轮不得分,且停止答题.每轮比赛的得分之和即为挑战者的总得分.现有甲、乙、丙三人作为挑战者参加节目答题,相关信息如下:
a.甲、乙两人参加比赛的得分统计如下,每个点的横坐标与纵坐标分别表示甲、乙两人在相同轮次的得分:
b.丙参加比赛的得分统计(已画完整)如下:
根据以上信息,回答下列问题:
(1)已知点A的坐标为(26,18),则此轮比赛中:甲的得分为 ,与甲同场答题的百人团中,有 人答对;
(2)这五轮比赛中,甲得分高于乙得分的比赛共有 轮,甲、乙、丙三人中总得分最高的为 ;
(3)设甲参加的第一轮至第五轮比赛时百人团答对人数的方差为,乙参加的第一轮至第五轮比赛时百人团答对人数的方差为,则 (填“>”“<”或“=”).
教 师 详 解 详 析
一 17.1 方差 17.2 用科学计算器计算方差
1.D 2.B 3.A 4.A 5.C
6.2 2
7.4或9 解: 甲组的平均数是×(11+12+13+14+15)=13(h),
则甲组的方差为[(11-13)2+(12-13)2+(13-13)2+(14-13)2+(15-13)2]=2;
乙组的平均数为=(h),
则乙组的方差为x-2+6-2+7-2+5-2+8-2.
由题意得x-2+6-2+7-2+5-2+8-2=2,
解得x=4或x=9.
故答案为4或9.
8.解:=(10+9.8+10+10.2)=10(mm),
=(10.1+10+9.9+10)=10(mm).
=[(10-10)2+(9.8-10)2+(10-10)2+(10.2-10)2]=0.02,
=[(10.1-10)2+(10-10)2+(9.9-10)2+(10-10)2]=0.005.
因为=,>,
所以乙机床生产的零件的质量更符合要求.
9.B
10.A 解: 根据题意,设数据x1,x2,…,xn的平均数为a,则数据x1+5,x2+5,…,xn+5的平均数为a+5,根据方差公式s2=[(x1-a)2+(x2-a)2+…+(xn-a)2]=3,
则s'2={[(x1+5)-(a+5)]2+[(x2+5)-(a+5)]2+…+[(xn+5)-(a+5)]2}=s2=3.故选A.
11. 26 12.(1)26 74 (2)2 乙 (3)<
1.方差的定义:如果用x1,x2,…,xn表示一组数据,用表示这组数据的平均数,那么每个数据与平均数的差的平方数的平均值叫这组数据的方差.方差用s2来表示.
2.方差的计算公式:
s2=[(x1-)2+(x2-)2+…+(xn-)2].
3.方差的意义:方差描述了一组数据波动的大小,方差的值越小,数据波动越小、越整齐.
归纳:(1)研究数据的离散程度可用方差.
(2)衡量一组数据的波动大小可用方差.
(3)常用方差比较平均数相同或接近的两组数据波动的大小.
(4)方差大,数据波动大;方差小,数据波动小.
1.(2020门头沟区期末)方差表示一组数据的 ( )
A.平均水平 B.数据个数
C.最大值或最小值 D.波动大小
2.甲、乙两人在相同情况下各射靶10次,两人命中环数的平均数均为7,方差=3,=1.2,则射击成绩较稳定的是 ( )
A.甲 B.乙
C.甲、乙一样 D.不能确定
3.甲和乙一起练习射击,第一轮10枪打完后两人的成绩如示.设他们这10次射击成绩的方差分别为,,下列关系正确的是( )
A.< B.> C.= D.无法确定
4.(2020房山区期末)某区学生在“垃圾分类知识”线上答题活动中,甲、乙、丙、丁四所学校参加线上答题的人数相同,四所学校答题所得分数的平均数和方差的数值如下表:
学校 甲 乙 丙 丁
平均数(分) 87 87 87 87
方差 0.027 0.043 0.036 0.029
则这四所学校成绩发挥最稳定的是 ( )
A.甲 B.乙 C.丙 D.丁
5.已知样本数据2,4,2,5,2,下列说法不正确的是 ( )
A.平均数是3 B.中位数是2
C.方差是2 D.众数是2
6.一组数据-2,-1,0,x,1的平均数是0,则x= ,方差s2= .
7.为了满足不同顾客对保温时效的需要,保温杯生产厂家研发了甲、乙两款保温杯.现从甲、乙两款中各随机抽取了5个保温杯,测得保温时效(单位:h)如下表:
甲组 11 12 13 14 15
乙组 x 6 7 5 8
如果甲、乙两款保温杯保温时效的方差是相等的,那么x= .
8.甲、乙两台机床同时生产直径为10 mm的零件,为了检验产品质量,质检员从两台机床生产的产品中各抽出4件进行测量,结果(单位:mm)如下:
甲机床 10 9.8 10 10.2
乙机床 10.1 10 9.9 10
请你通过计算判断哪台机床生产的零件的质量更符合要求
9.一组数据0,-1,6,1,x的众数为-1,则这组数据的方差是 ( )
A.2 B. C. D.
10.如果一组数据x1,x2,…,xn的方差是3,那么另一组数据x1+5,x2+5,…,xn+5的方差是 ( )
A.3 B.8 C.9 D.14
11.若样本数据1,2,3,x的平均数为5,样本数据1,2,3,x,y的平均数为6,则样本数据1,2,3,x,y的方差是 .
12.(2021海淀区二模)品味诗词之美,传承中华文明,央视节目《中国诗词大会》备受大众欢迎.节目规则如下:由100位诗词爱好者组成的百人团与挑战者共同答题,每位挑战者最多可答五轮题.每轮比赛答题时,若挑战者答对,则百人团答错的人数即为选手该轮得分;若挑战者答错,则该轮不得分,且停止答题.每轮比赛的得分之和即为挑战者的总得分.现有甲、乙、丙三人作为挑战者参加节目答题,相关信息如下:
a.甲、乙两人参加比赛的得分统计如下,每个点的横坐标与纵坐标分别表示甲、乙两人在相同轮次的得分:
b.丙参加比赛的得分统计(已画完整)如下:
根据以上信息,回答下列问题:
(1)已知点A的坐标为(26,18),则此轮比赛中:甲的得分为 ,与甲同场答题的百人团中,有 人答对;
(2)这五轮比赛中,甲得分高于乙得分的比赛共有 轮,甲、乙、丙三人中总得分最高的为 ;
(3)设甲参加的第一轮至第五轮比赛时百人团答对人数的方差为,乙参加的第一轮至第五轮比赛时百人团答对人数的方差为,则 (填“>”“<”或“=”).
教 师 详 解 详 析
一 17.1 方差 17.2 用科学计算器计算方差
1.D 2.B 3.A 4.A 5.C
6.2 2
7.4或9 解: 甲组的平均数是×(11+12+13+14+15)=13(h),
则甲组的方差为[(11-13)2+(12-13)2+(13-13)2+(14-13)2+(15-13)2]=2;
乙组的平均数为=(h),
则乙组的方差为x-2+6-2+7-2+5-2+8-2.
由题意得x-2+6-2+7-2+5-2+8-2=2,
解得x=4或x=9.
故答案为4或9.
8.解:=(10+9.8+10+10.2)=10(mm),
=(10.1+10+9.9+10)=10(mm).
=[(10-10)2+(9.8-10)2+(10-10)2+(10.2-10)2]=0.02,
=[(10.1-10)2+(10-10)2+(9.9-10)2+(10-10)2]=0.005.
因为=,>,
所以乙机床生产的零件的质量更符合要求.
9.B
10.A 解: 根据题意,设数据x1,x2,…,xn的平均数为a,则数据x1+5,x2+5,…,xn+5的平均数为a+5,根据方差公式s2=[(x1-a)2+(x2-a)2+…+(xn-a)2]=3,
则s'2={[(x1+5)-(a+5)]2+[(x2+5)-(a+5)]2+…+[(xn+5)-(a+5)]2}=s2=3.故选A.
11. 26 12.(1)26 74 (2)2 乙 (3)<
同课章节目录
