北京课改版数学八年级下册同步课时练习:第十四章 一次函数 复习小结(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:第十四章 一次函数 复习小结(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 229.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 10:42:11 | ||
图片预览


文档简介
复习小结
类型之一 自变量x的取值范围
1.在函数y=中,自变量x的取值范围是 .
2.函数y=的自变量x的取值范围是 .
3.在函数y=-中,自变量x的取值范围是 .
类型之二 平面直角坐标系
4.已知点P位于第四象限,且距离x轴4个单位长度,距离y轴3个单位长度,则点P的坐标是 ( )
A.(-4,3) B.(4,-3) C.(3,-4) D.(-3,4)
5.若点A(n-2,n+1)在x轴上,则n的值为 ( )
A.1 B.2 C.-1 D.-2
6. (2020昌平区二模)昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭、文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑.如分别以正东、正北方向为x轴,y轴建立平面直角坐标系,若表示文节亭所在的点的坐标为(2,0),表示园中园所在的点的坐标为(-1,2),则表示弘文阁所在的点的坐标为( )
A.(-2,-3) B.(-2,-2) C.(-3,-3) D.(-3,-4)
7.(2019北京师大附中期中)如动点P在平面直角坐标系中,按中箭头所示方向运动:第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律经过第2019次运动后,动点P的坐标是( )
A.(2018,2) B.(2019,2) C.(2019,1) D.(2017,1)
类型之三 函数象
8.(2019东城区期末)如果规定[x]表示不大于x的最大整数,例如[2.1]=2,[-2.1]=-3,那么函数y=x-[x](-3≤x≤3)的象为 ( )
9.某天,某同学早上8点坐车从余姚书馆出发去60千米外的宁波大学,汽车离开余姚书馆的距离s(千米)与所用时间t(分)之间的函数关系如示.已知汽车在途中停车加油一次,则下列描述不正确的是( )
A.汽车在途中加油用了10分钟
B.若OA∥BC,则加满油以后的速度为80千米/时
C.若汽车加油后的速度是90千米/时,则a=25
D.该同学8:55到达宁波大学
类型之四 一次函数的象与性质
10.一次函数y=-3x+1的象不经过 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
11.已知点A(5,y1)和点B(4,y2)都在直线y=x+b上,则y1与y2的大小关系为 .
12.(2019朝阳区期末)直线l的函数表达式为y=-x+4,分别交x轴,y轴于点A,B.
(1)写出A,B两点的坐标,并在画出直线l(不需列表);
(2)将直线l向左平移4个单位长度得到直线l1,在中画出直线l1,则直线l1的函数表达式是 .
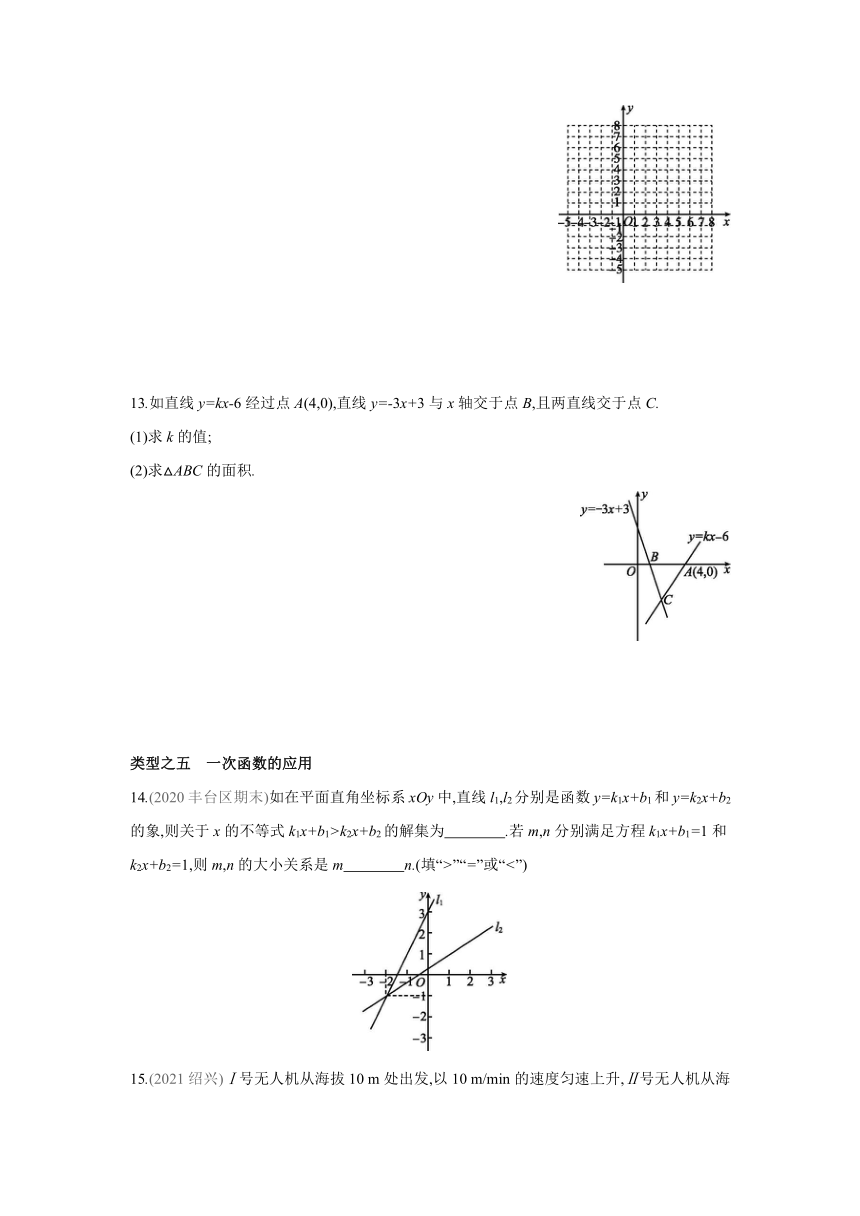
13.如直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值;
(2)求△ABC的面积.
类型之五 一次函数的应用
14.(2020丰台区期末)如在平面直角坐标系xOy中,直线l1,l2分别是函数y=k1x+b1和y=k2x+b2的象,则关于x的不等式k1x+b1>k2x+b2的解集为 .若m,n分别满足方程k1x+b1=1和k2x+b2=1,则m,n的大小关系是m n.(填“>”“=”或“<”)
15.(2021绍兴)Ⅰ号无人机从海拔10 m处出发,以10 m/min的速度匀速上升,Ⅱ号无人机从海拔30 m处同时出发,以a m/min的速度匀速上升,经过5 min两架无人机位于同一海拔b m.无人机的海拔y(m)与时间x(min)的关系如两架无人机都上升了15 min.
(1)求b的值及Ⅱ号无人机海拔y(m)与时间x(min)的函数表达式;
(2)无人机上升多长时间后,Ⅰ号无人机比Ⅱ号无人机高28 m
详 解
1.x≠-2
2.x≥
3.-2≤x≤3
4.C 5.C
6.B 解: 如所示.
7.B 解: 根据动点P在平面直角坐标系中按中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),则第4次运动到点(4,0),第5次接着运动到点(5,1)……
则横坐标为运动次数,经过第2019次运动后,动点P的横坐标为2019,
纵坐标为1,0,2,0,每4次一轮,
2019÷4=504……3,
故纵坐标为四个数中第3个数,即为2.
则经过第2019次运动后,动点P的坐标是(2019,2).
8.A 解: 当-3≤x<-2时,y=x-[x]=x-(-3)=x+3,y随x的增大而增大,当x=-3时,取得最小值,此时y=0,同理可得,其他各段内的函数象与-3≤x<-2这段内的函数象是一样的.
9.C 解: A项,由象可知,汽车在途中加油时间为25至35分钟,共10分钟,故本选项正确;
B项,因为OA∥BC,所以=,解得a=,所以加满油以后的速度==80千米/时,故本选项正确;
C项,由题意,得=90,解得a=30,本选项错误;
D项,该同学8:55到达宁波大学,正确.
故选C.
10.C 解: ∵一次函数y=-3x+1,k=-3<0,b=1>0,
∴该函数象经过第一、二、四象限,不经过第三象限.
11.y1>y2
12.解:(1)令x=0,得y=-x+4=4,∴点B的坐标为(0,4);令y=-x+4=0,解得x=6,∴点A的坐标为(6,0).
画出直线l如.
(2)将直线l向左平移4个单位长度得到直线l1,如所示,则直线l1的函数表达式为y=-(x+4)+4=-x+.
13.解: (1)将点A的坐标(4,0)代入函数表达式y=kx-6求出k;
(2)先求出点B的坐标,再求出线段AB的长与点C的坐标即可求出△ABC的面积.
解:(1)∵直线y=kx-6经过点A(4,0),
∴4k-6=0,即k=.
(2)∵直线y=-3x+3与x轴交于点B,
∴令-3x+3=0,
解得x=1,
∴点B的坐标为(1,0).
∵两直线交于点C,
∴由解得
∴点C的坐标为(2,-3),
∴△ABC的面积为×AB×|-3|=×3×|-3|=.
14.x>-2 <
15.解:(1)b=10+10×5=60.设Ⅱ号无人机y与x的函数表达式为y=kx+t,
将(0,30),(5,60)代入上式,得
解得
故Ⅱ号无人机海拔y与时间x的函数表达式为y=6x+30(0≤x≤15).
(2)设Ⅰ号无人机y与x的函数表达式为y=k1x+b1,则解得
∴y=10x+10(0≤x≤15).
由题意,得(10x+10)-(6x+30)=28,解得x=12<15,
故无人机上升12 min后,Ⅰ号无人机比Ⅱ号无人机高28 m.
类型之一 自变量x的取值范围
1.在函数y=中,自变量x的取值范围是 .
2.函数y=的自变量x的取值范围是 .
3.在函数y=-中,自变量x的取值范围是 .
类型之二 平面直角坐标系
4.已知点P位于第四象限,且距离x轴4个单位长度,距离y轴3个单位长度,则点P的坐标是 ( )
A.(-4,3) B.(4,-3) C.(3,-4) D.(-3,4)
5.若点A(n-2,n+1)在x轴上,则n的值为 ( )
A.1 B.2 C.-1 D.-2
6. (2020昌平区二模)昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭、文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑.如分别以正东、正北方向为x轴,y轴建立平面直角坐标系,若表示文节亭所在的点的坐标为(2,0),表示园中园所在的点的坐标为(-1,2),则表示弘文阁所在的点的坐标为( )
A.(-2,-3) B.(-2,-2) C.(-3,-3) D.(-3,-4)
7.(2019北京师大附中期中)如动点P在平面直角坐标系中,按中箭头所示方向运动:第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律经过第2019次运动后,动点P的坐标是( )
A.(2018,2) B.(2019,2) C.(2019,1) D.(2017,1)
类型之三 函数象
8.(2019东城区期末)如果规定[x]表示不大于x的最大整数,例如[2.1]=2,[-2.1]=-3,那么函数y=x-[x](-3≤x≤3)的象为 ( )
9.某天,某同学早上8点坐车从余姚书馆出发去60千米外的宁波大学,汽车离开余姚书馆的距离s(千米)与所用时间t(分)之间的函数关系如示.已知汽车在途中停车加油一次,则下列描述不正确的是( )
A.汽车在途中加油用了10分钟
B.若OA∥BC,则加满油以后的速度为80千米/时
C.若汽车加油后的速度是90千米/时,则a=25
D.该同学8:55到达宁波大学
类型之四 一次函数的象与性质
10.一次函数y=-3x+1的象不经过 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
11.已知点A(5,y1)和点B(4,y2)都在直线y=x+b上,则y1与y2的大小关系为 .
12.(2019朝阳区期末)直线l的函数表达式为y=-x+4,分别交x轴,y轴于点A,B.
(1)写出A,B两点的坐标,并在画出直线l(不需列表);
(2)将直线l向左平移4个单位长度得到直线l1,在中画出直线l1,则直线l1的函数表达式是 .
13.如直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值;
(2)求△ABC的面积.
类型之五 一次函数的应用
14.(2020丰台区期末)如在平面直角坐标系xOy中,直线l1,l2分别是函数y=k1x+b1和y=k2x+b2的象,则关于x的不等式k1x+b1>k2x+b2的解集为 .若m,n分别满足方程k1x+b1=1和k2x+b2=1,则m,n的大小关系是m n.(填“>”“=”或“<”)
15.(2021绍兴)Ⅰ号无人机从海拔10 m处出发,以10 m/min的速度匀速上升,Ⅱ号无人机从海拔30 m处同时出发,以a m/min的速度匀速上升,经过5 min两架无人机位于同一海拔b m.无人机的海拔y(m)与时间x(min)的关系如两架无人机都上升了15 min.
(1)求b的值及Ⅱ号无人机海拔y(m)与时间x(min)的函数表达式;
(2)无人机上升多长时间后,Ⅰ号无人机比Ⅱ号无人机高28 m
详 解
1.x≠-2
2.x≥
3.-2≤x≤3
4.C 5.C
6.B 解: 如所示.
7.B 解: 根据动点P在平面直角坐标系中按中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),则第4次运动到点(4,0),第5次接着运动到点(5,1)……
则横坐标为运动次数,经过第2019次运动后,动点P的横坐标为2019,
纵坐标为1,0,2,0,每4次一轮,
2019÷4=504……3,
故纵坐标为四个数中第3个数,即为2.
则经过第2019次运动后,动点P的坐标是(2019,2).
8.A 解: 当-3≤x<-2时,y=x-[x]=x-(-3)=x+3,y随x的增大而增大,当x=-3时,取得最小值,此时y=0,同理可得,其他各段内的函数象与-3≤x<-2这段内的函数象是一样的.
9.C 解: A项,由象可知,汽车在途中加油时间为25至35分钟,共10分钟,故本选项正确;
B项,因为OA∥BC,所以=,解得a=,所以加满油以后的速度==80千米/时,故本选项正确;
C项,由题意,得=90,解得a=30,本选项错误;
D项,该同学8:55到达宁波大学,正确.
故选C.
10.C 解: ∵一次函数y=-3x+1,k=-3<0,b=1>0,
∴该函数象经过第一、二、四象限,不经过第三象限.
11.y1>y2
12.解:(1)令x=0,得y=-x+4=4,∴点B的坐标为(0,4);令y=-x+4=0,解得x=6,∴点A的坐标为(6,0).
画出直线l如.
(2)将直线l向左平移4个单位长度得到直线l1,如所示,则直线l1的函数表达式为y=-(x+4)+4=-x+.
13.解: (1)将点A的坐标(4,0)代入函数表达式y=kx-6求出k;
(2)先求出点B的坐标,再求出线段AB的长与点C的坐标即可求出△ABC的面积.
解:(1)∵直线y=kx-6经过点A(4,0),
∴4k-6=0,即k=.
(2)∵直线y=-3x+3与x轴交于点B,
∴令-3x+3=0,
解得x=1,
∴点B的坐标为(1,0).
∵两直线交于点C,
∴由解得
∴点C的坐标为(2,-3),
∴△ABC的面积为×AB×|-3|=×3×|-3|=.
14.x>-2 <
15.解:(1)b=10+10×5=60.设Ⅱ号无人机y与x的函数表达式为y=kx+t,
将(0,30),(5,60)代入上式,得
解得
故Ⅱ号无人机海拔y与时间x的函数表达式为y=6x+30(0≤x≤15).
(2)设Ⅰ号无人机y与x的函数表达式为y=k1x+b1,则解得
∴y=10x+10(0≤x≤15).
由题意,得(10x+10)-(6x+30)=28,解得x=12<15,
故无人机上升12 min后,Ⅰ号无人机比Ⅱ号无人机高28 m.
同课章节目录
