北京课改版数学八年级下册同步课时练习:第十四章 一次函数 单元测试(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级下册同步课时练习:第十四章 一次函数 单元测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 10:43:18 | ||
图片预览


文档简介
第十四章 一次函数 单元测试
一、选择题(本题共8个小题,每小题5分,共40分)
1.已知点A(4,5),则点A关于x轴对称的点A'的坐标是 ( )
A.(-5,-4) B.(-4,5)
C.(-4,-5) D.(4,-5)
2.函数y=的自变量的取值范围是 ( )
A.x≠0 B.x≠1 C.x≥1 D.x>1
3.下面哪个点在函数y=x+1的象上 ( )
A.(2,1) B.(-2,1) C.(2,0) D.(-2,0)
4.一次函数y=-3x-1的象经过的象限是 ( )
A.第一、二、三象限 B.第二、三、四象限
C.第一、二、四象限 D.第一、三、四象限
5.若正比例函数y=(1-2m)x的象经过点A(x1,y1)和点B(x2,y2),当x1y2,则m的取值范围是 ( )
A.m<0 B.m>0 C.m< D.m>
6.已知一次函数的象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为 ( )
A.y=-x-2 B.y=-x+10
C.y=-x-6 D.y=-x-1
7.某快递公司每天9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数象如示,那么两仓库快递件数相同时的时间为 ( )
A.9:15 B.9:20 C.9:25 D.9:30
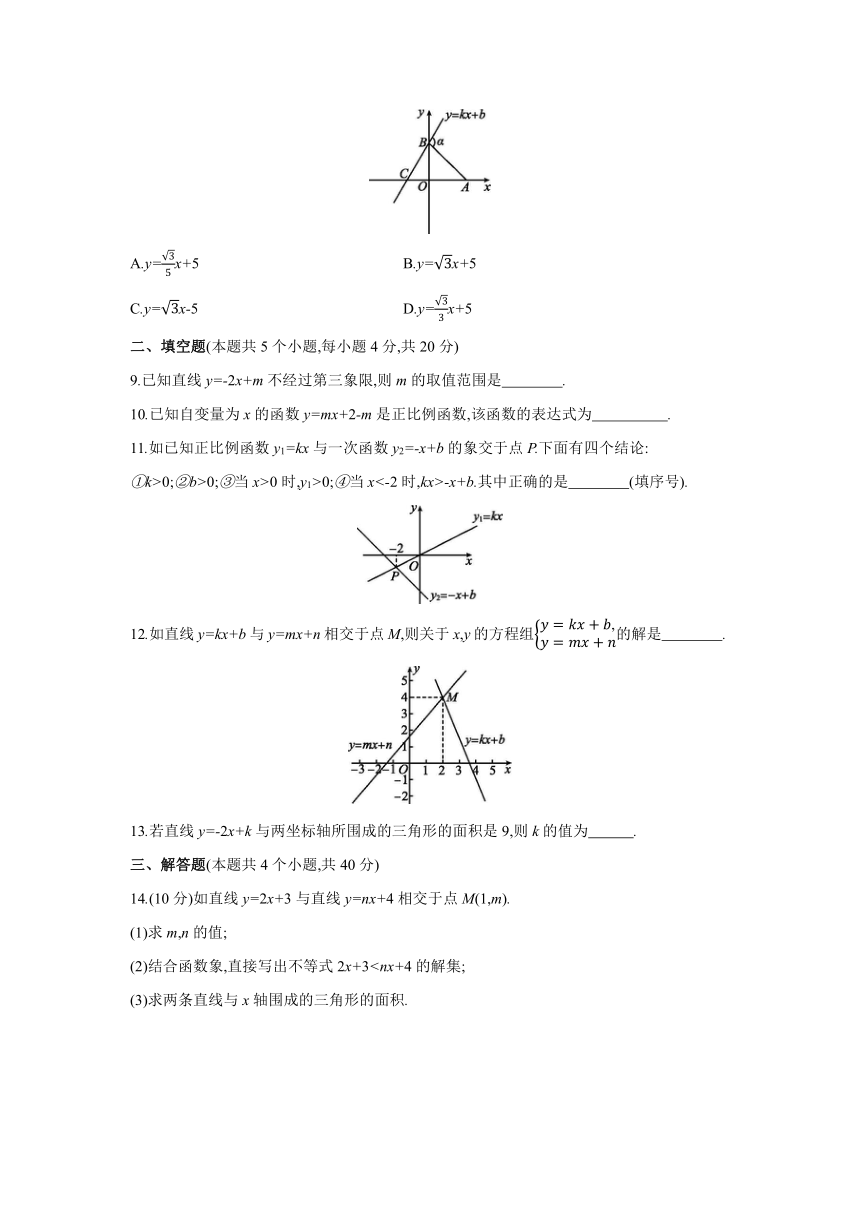
8.如已知点A的坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为 ( )
A.y=x+5 B.y=x+5
C.y=x-5 D.y=x+5
二、填空题(本题共5个小题,每小题4分,共20分)
9.已知直线y=-2x+m不经过第三象限,则m的取值范围是 .
10.已知自变量为x的函数y=mx+2-m是正比例函数,该函数的表达式为 .
11.如已知正比例函数y1=kx与一次函数y2=-x+b的象交于点P.下面有四个结论:
①k>0;②b>0;③当x>0时,y1>0;④当x<-2时,kx>-x+b.其中正确的是 (填序号).
12.如直线y=kx+b与y=mx+n相交于点M,则关于x,y的方程组的解是 .
13.若直线y=-2x+k与两坐标轴所围成的三角形的面积是9,则k的值为 .
三、解答题(本题共4个小题,共40分)
14.(10分)如直线y=2x+3与直线y=nx+4相交于点M(1,m).
(1)求m,n的值;
(2)结合函数象,直接写出不等式2x+3(3)求两条直线与x轴围成的三角形的面积.
15.(10分)某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本及利润如下表,设每天生产A种品牌白酒x瓶,每天获利y元.
A B
成本(元/瓶) 50 35
利润(元/瓶) 20 15
(1)请写出y关于x的函数表达式(不必写出自变量的取值范围);
(2)如果该酒厂每天投入成本27000元,那么每天获利多少元
16.(9分)已知M(3,2),点P在x轴上,点Q在y轴上.
(1)若N(-2,1),PM+PN最短,求点P的坐标;
(2)若N(1,-1),QM+QN最短,求点Q的坐标.
17.(11分)甲、乙两地相距300 km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE所在直线的函数表达式;
(3)求轿车从甲地出发后经过多长时间追上货车.
详 解
1.D 2.C 3.D 4.B
5.D 解: 由题意,知y随x的增大而减小,
∴1-2m<0,解得m>.故选D.
6.B 7.B
8.B 解: ∵点A的坐标为(5,0),∴OA=5.
∵∠BCA=60°,∠α=105°,
∴∠BAC=105°-60°=45°,∴△AOB是等腰直角三角形,∴AO=BO=5,∴B(0,5).
∵∠CBO=90°-∠BCA=30°,∴BC=2CO,
BO==CO=5,
∴CO=,∴C-,0,
把B(0,5)和C-,0代入y=kx+b,得解得
∴直线的函数表达式为y=x+5.故选B.
9.m≥0
10.y=2x
11.①③ 解: ∵直线y1=kx经过第一、三象限,∴k>0,故①正确;∵y2=-x+b与y轴交点在负半轴,∴b<0,故②错误;∵正比例函数y1=kx经过原点,且y随x的增大而增大,∴当x>0时,y1>0;故③正确;当x<-2时,正比例函数y1=kx的象在一次函数y2=-x+b象的下方,即kx<-x+b,故④错误.故答案为①③.
12. 解: ∵直线y=kx+b与y=mx+n相交于点M(2,4),
∴关于x,y的方程组的解是
13.±6
14.解:(1)∵直线y=2x+3与直线y=nx+4相交于点M(1,m),∴m=2+3=5,∴M(1,5),
∴5=n+4,∴n=1.
(2)由象可知不等式2x+3(3)由直线y=2x+3与直线y=x+4可知,两直线与x轴的交点分别为-,0,(-4,0),
∴两条直线与x轴围成的三角形的面积为×-+4×5=.
15.解:(1)依题意,得y=20x+15(600-x),即y=5x+9000.
(2)依题意,得50x+35(600-x)=27000.
解得x=400,
∴y=5×400+9000=11000.
答:每天获利11000元.
16.解:(1)作点M关于x轴的对称点M'.
∵M(3,2),∴M'(3,-2).
设直线M'N的表达式为y=kx+b,
∴解得
∴直线M'N的表达式为y=-x-.直线M'N与x轴的交点即为所求点P.
∵点P的纵坐标为0,∴-x-=0,解得x=-,∴P-,0.
(2)作点N关于y轴的对称点N'.
∵N(1,-1),∴N'(-1,-1).
设直线MN'的表达式为y=ax+c,
∴解得
∴直线MN'的表达式为y=x-.直线MN'与y轴的交点即为所求点Q.
∵点Q的横坐标为0,
∴y=x-=-,
∴Q0,-.
17.解:(1)线段CD表示轿车在途中停留了2.5-2=0.5(h).
(2)设线段DE所在直线的函数表达式为y=kx+b(k≠0).
把点D,E的坐标(2.5,80),(4.5,300)分别代入y=kx+b,
得
解得
∴线段DE所在直线的函数表达式为y=110x-195.
(3)∵点A的坐标为(5,300),设直线OA的函数表达式为y=ax(a≠0).
将点A的坐标代入y=ax,
得300=5a,解得a=60,
∴直线OA的函数表达式为y=60x.
由象,得轿车在DE段追上货车.
令60x=110x-195,
解得x=3.9,
∴3.9-1=2.9(h).
答:轿车从甲地出发后经过2.9 h追上货车.
一、选择题(本题共8个小题,每小题5分,共40分)
1.已知点A(4,5),则点A关于x轴对称的点A'的坐标是 ( )
A.(-5,-4) B.(-4,5)
C.(-4,-5) D.(4,-5)
2.函数y=的自变量的取值范围是 ( )
A.x≠0 B.x≠1 C.x≥1 D.x>1
3.下面哪个点在函数y=x+1的象上 ( )
A.(2,1) B.(-2,1) C.(2,0) D.(-2,0)
4.一次函数y=-3x-1的象经过的象限是 ( )
A.第一、二、三象限 B.第二、三、四象限
C.第一、二、四象限 D.第一、三、四象限
5.若正比例函数y=(1-2m)x的象经过点A(x1,y1)和点B(x2,y2),当x1
A.m<0 B.m>0 C.m< D.m>
6.已知一次函数的象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为 ( )
A.y=-x-2 B.y=-x+10
C.y=-x-6 D.y=-x-1
7.某快递公司每天9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数象如示,那么两仓库快递件数相同时的时间为 ( )
A.9:15 B.9:20 C.9:25 D.9:30
8.如已知点A的坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为 ( )
A.y=x+5 B.y=x+5
C.y=x-5 D.y=x+5
二、填空题(本题共5个小题,每小题4分,共20分)
9.已知直线y=-2x+m不经过第三象限,则m的取值范围是 .
10.已知自变量为x的函数y=mx+2-m是正比例函数,该函数的表达式为 .
11.如已知正比例函数y1=kx与一次函数y2=-x+b的象交于点P.下面有四个结论:
①k>0;②b>0;③当x>0时,y1>0;④当x<-2时,kx>-x+b.其中正确的是 (填序号).
12.如直线y=kx+b与y=mx+n相交于点M,则关于x,y的方程组的解是 .
13.若直线y=-2x+k与两坐标轴所围成的三角形的面积是9,则k的值为 .
三、解答题(本题共4个小题,共40分)
14.(10分)如直线y=2x+3与直线y=nx+4相交于点M(1,m).
(1)求m,n的值;
(2)结合函数象,直接写出不等式2x+3
15.(10分)某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本及利润如下表,设每天生产A种品牌白酒x瓶,每天获利y元.
A B
成本(元/瓶) 50 35
利润(元/瓶) 20 15
(1)请写出y关于x的函数表达式(不必写出自变量的取值范围);
(2)如果该酒厂每天投入成本27000元,那么每天获利多少元
16.(9分)已知M(3,2),点P在x轴上,点Q在y轴上.
(1)若N(-2,1),PM+PN最短,求点P的坐标;
(2)若N(1,-1),QM+QN最短,求点Q的坐标.
17.(11分)甲、乙两地相距300 km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE所在直线的函数表达式;
(3)求轿车从甲地出发后经过多长时间追上货车.
详 解
1.D 2.C 3.D 4.B
5.D 解: 由题意,知y随x的增大而减小,
∴1-2m<0,解得m>.故选D.
6.B 7.B
8.B 解: ∵点A的坐标为(5,0),∴OA=5.
∵∠BCA=60°,∠α=105°,
∴∠BAC=105°-60°=45°,∴△AOB是等腰直角三角形,∴AO=BO=5,∴B(0,5).
∵∠CBO=90°-∠BCA=30°,∴BC=2CO,
BO==CO=5,
∴CO=,∴C-,0,
把B(0,5)和C-,0代入y=kx+b,得解得
∴直线的函数表达式为y=x+5.故选B.
9.m≥0
10.y=2x
11.①③ 解: ∵直线y1=kx经过第一、三象限,∴k>0,故①正确;∵y2=-x+b与y轴交点在负半轴,∴b<0,故②错误;∵正比例函数y1=kx经过原点,且y随x的增大而增大,∴当x>0时,y1>0;故③正确;当x<-2时,正比例函数y1=kx的象在一次函数y2=-x+b象的下方,即kx<-x+b,故④错误.故答案为①③.
12. 解: ∵直线y=kx+b与y=mx+n相交于点M(2,4),
∴关于x,y的方程组的解是
13.±6
14.解:(1)∵直线y=2x+3与直线y=nx+4相交于点M(1,m),∴m=2+3=5,∴M(1,5),
∴5=n+4,∴n=1.
(2)由象可知不等式2x+3
∴两条直线与x轴围成的三角形的面积为×-+4×5=.
15.解:(1)依题意,得y=20x+15(600-x),即y=5x+9000.
(2)依题意,得50x+35(600-x)=27000.
解得x=400,
∴y=5×400+9000=11000.
答:每天获利11000元.
16.解:(1)作点M关于x轴的对称点M'.
∵M(3,2),∴M'(3,-2).
设直线M'N的表达式为y=kx+b,
∴解得
∴直线M'N的表达式为y=-x-.直线M'N与x轴的交点即为所求点P.
∵点P的纵坐标为0,∴-x-=0,解得x=-,∴P-,0.
(2)作点N关于y轴的对称点N'.
∵N(1,-1),∴N'(-1,-1).
设直线MN'的表达式为y=ax+c,
∴解得
∴直线MN'的表达式为y=x-.直线MN'与y轴的交点即为所求点Q.
∵点Q的横坐标为0,
∴y=x-=-,
∴Q0,-.
17.解:(1)线段CD表示轿车在途中停留了2.5-2=0.5(h).
(2)设线段DE所在直线的函数表达式为y=kx+b(k≠0).
把点D,E的坐标(2.5,80),(4.5,300)分别代入y=kx+b,
得
解得
∴线段DE所在直线的函数表达式为y=110x-195.
(3)∵点A的坐标为(5,300),设直线OA的函数表达式为y=ax(a≠0).
将点A的坐标代入y=ax,
得300=5a,解得a=60,
∴直线OA的函数表达式为y=60x.
由象,得轿车在DE段追上货车.
令60x=110x-195,
解得x=3.9,
∴3.9-1=2.9(h).
答:轿车从甲地出发后经过2.9 h追上货车.
同课章节目录
