华师大版数学七年级下册 第10章轴对称、平移与旋转10.3.2旋转的特征教案
文档属性
| 名称 | 华师大版数学七年级下册 第10章轴对称、平移与旋转10.3.2旋转的特征教案 | 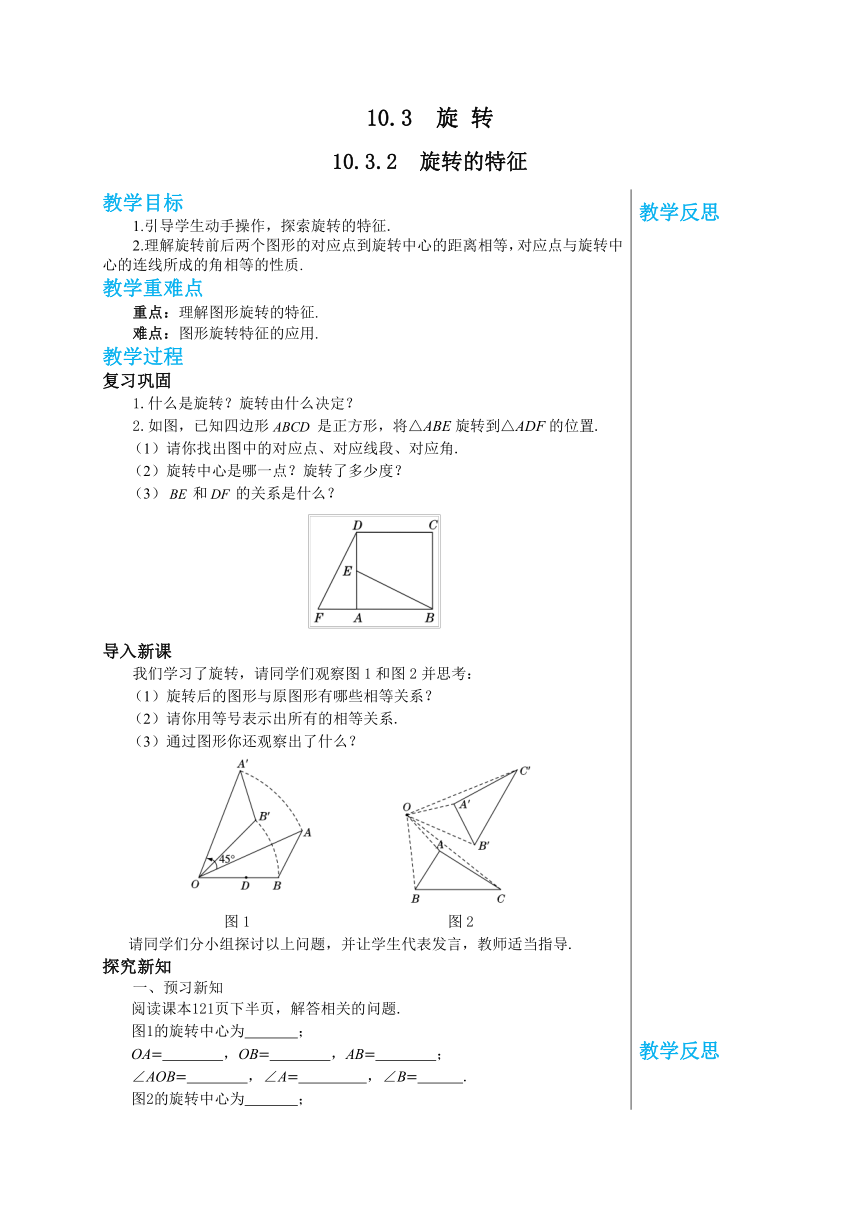 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 11:00:07 | ||
图片预览


文档简介
10.3 旋 转
10.3.2 旋转的特征
教学目标 1.引导学生动手操作,探索旋转的特征. 2.理解旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角相等的性质. 教学重难点 重点:理解图形旋转的特征. 难点:图形旋转特征的应用. 教学过程 复习巩固 1.什么是旋转?旋转由什么决定? 2.如图,已知四边形是正方形,将△ABE旋转到△ADF的位置. (1)请你找出图中的对应点、对应线段、对应角. (2)旋转中心是哪一点?旋转了多少度? (3)和的关系是什么? 导入新课 我们学习了旋转,请同学们观察图1和图2并思考: (1)旋转后的图形与原图形有哪些相等关系? (2)请你用等号表示出所有的相等关系. (3)通过图形你还观察出了什么? 图1 图2 请同学们分小组探讨以上问题,并让学生代表发言,教师适当指导. 探究新知 一、预习新知 阅读课本121页下半页,解答相关的问题. 图1的旋转中心为 ; OA ,OB ,AB ; ∠AOB ,∠A ,∠B . 图2的旋转中心为 ; OA ,OB ,AB ; OC ,BC ,CA ; ∠CAB ,∠ABC ,∠BCA . 二、合作探究 请同学们对比图1和图2的相同点,根据上面的问题总结旋转的特征(学生代表发言,老师点评并进行总结): (1)图形中每一点都绕着旋转中心按相同的方向旋转了同样大小的角度. (2)对应点到旋转中心的距离相等. (3)对应线段相等,对应角相等. (4)图形的形状、大小都没有变化,而只改变了位置. 例1 如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合. (1)△ABC旋转了多少度? (2)连结CE,试判断△AEC的形状. (3)求∠AEC的度数. 【问题探索】 (引发学生思考)(1)图中哪些角是旋转角?旋转中对应角有什么特征?(2)AC与AE有什么关系?旋转过程中对应线段有什么特征?(3)∠AEC在哪个三角形中?等腰三角形有什么特征? 【解】(1)由图可知,∠BAD是旋转角. ∵∠BAC=40°,点C,A,D共线, ∴∠BAD=140°, 即△ABC旋转了140°. (2)由旋转的性质可知,AC=AE, ∴△AEC是等腰三角形. (3)由旋转的性质可知,∠CAE=∠BAD=140°. 又∵AC=AE, ∴∠AEC=(180°-140°)÷2=20°. 【总结】(学生总结,老师点评)本题考查的是旋转变换的性质,理解旋转三要素旋转中心、旋转方向、旋转角度的概念,掌握旋转变换的性质是解题的关键. 例2 如图,△ABC绕点C旋转后,顶点A的对应点为点D,试确定顶点B的对应点的位置,以及旋转后的三角形. 【问题探索】(引发学生思考)旋转要注意哪三个要素? 【解】(1)如题图,连结CD; (2)以CB为一边作∠BCE,使得∠BCE=∠ACD; (3)在射线CE上截取CB′=CB,则B′即为所求的点B的对应点; (4)连结DB′,则△DB′C就是△ABC绕C点旋转后的三角形. 【总结】(学生总结,老师点评)旋转作图时,首先必须确定旋转中心、旋转方向和旋转角,并根据对应点到旋转中心的距离相等找到对应点. 课堂练习 1.如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是 ( ) A.35° B.45° C.55° D.65° 2.如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连结AD.下列结论一定正确的是 ( ) A.∠ABD=∠E B.∠CBE+∠DBE<180° C.AD=BC D.AD∥BC 3.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE旋转后得到的图形. (1)旋转中心是哪一点? (2)旋转了多少度? (3)如果连结EF,那么△AEF是怎样的三角形? 参考答案 1.C 2.D 3.解:(1)旋转中心是A点. (2)∵△ABF是由△ADE旋转而成的,∴B是D的对应点, ∴∠DAB就是旋转角,即旋转了90°. (3)∵∠EAF=90°(与旋转角相等)且AF=AE, ∴△AEF是等腰直角三角形. 课堂小结 布置作业 课本第122页练习第1,2,3题. 板书设计 第10章 轴对称、平移与旋转 10.3 旋 转 10.3.2 旋转的特征 旋转的特征: (1)图形中每一点都绕着旋转中心按相同的方向旋转了同样大小的角度. (2)对应点到旋转中心的距离相等. (3)对应线段相等,对应角相等. (4)图形的形状、大小都没有变化,而只改变了位置. 例1 例2 教学反思 教学反思 教学反思 教学反思
10.3.2 旋转的特征
教学目标 1.引导学生动手操作,探索旋转的特征. 2.理解旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角相等的性质. 教学重难点 重点:理解图形旋转的特征. 难点:图形旋转特征的应用. 教学过程 复习巩固 1.什么是旋转?旋转由什么决定? 2.如图,已知四边形是正方形,将△ABE旋转到△ADF的位置. (1)请你找出图中的对应点、对应线段、对应角. (2)旋转中心是哪一点?旋转了多少度? (3)和的关系是什么? 导入新课 我们学习了旋转,请同学们观察图1和图2并思考: (1)旋转后的图形与原图形有哪些相等关系? (2)请你用等号表示出所有的相等关系. (3)通过图形你还观察出了什么? 图1 图2 请同学们分小组探讨以上问题,并让学生代表发言,教师适当指导. 探究新知 一、预习新知 阅读课本121页下半页,解答相关的问题. 图1的旋转中心为 ; OA ,OB ,AB ; ∠AOB ,∠A ,∠B . 图2的旋转中心为 ; OA ,OB ,AB ; OC ,BC ,CA ; ∠CAB ,∠ABC ,∠BCA . 二、合作探究 请同学们对比图1和图2的相同点,根据上面的问题总结旋转的特征(学生代表发言,老师点评并进行总结): (1)图形中每一点都绕着旋转中心按相同的方向旋转了同样大小的角度. (2)对应点到旋转中心的距离相等. (3)对应线段相等,对应角相等. (4)图形的形状、大小都没有变化,而只改变了位置. 例1 如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合. (1)△ABC旋转了多少度? (2)连结CE,试判断△AEC的形状. (3)求∠AEC的度数. 【问题探索】 (引发学生思考)(1)图中哪些角是旋转角?旋转中对应角有什么特征?(2)AC与AE有什么关系?旋转过程中对应线段有什么特征?(3)∠AEC在哪个三角形中?等腰三角形有什么特征? 【解】(1)由图可知,∠BAD是旋转角. ∵∠BAC=40°,点C,A,D共线, ∴∠BAD=140°, 即△ABC旋转了140°. (2)由旋转的性质可知,AC=AE, ∴△AEC是等腰三角形. (3)由旋转的性质可知,∠CAE=∠BAD=140°. 又∵AC=AE, ∴∠AEC=(180°-140°)÷2=20°. 【总结】(学生总结,老师点评)本题考查的是旋转变换的性质,理解旋转三要素旋转中心、旋转方向、旋转角度的概念,掌握旋转变换的性质是解题的关键. 例2 如图,△ABC绕点C旋转后,顶点A的对应点为点D,试确定顶点B的对应点的位置,以及旋转后的三角形. 【问题探索】(引发学生思考)旋转要注意哪三个要素? 【解】(1)如题图,连结CD; (2)以CB为一边作∠BCE,使得∠BCE=∠ACD; (3)在射线CE上截取CB′=CB,则B′即为所求的点B的对应点; (4)连结DB′,则△DB′C就是△ABC绕C点旋转后的三角形. 【总结】(学生总结,老师点评)旋转作图时,首先必须确定旋转中心、旋转方向和旋转角,并根据对应点到旋转中心的距离相等找到对应点. 课堂练习 1.如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是 ( ) A.35° B.45° C.55° D.65° 2.如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连结AD.下列结论一定正确的是 ( ) A.∠ABD=∠E B.∠CBE+∠DBE<180° C.AD=BC D.AD∥BC 3.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE旋转后得到的图形. (1)旋转中心是哪一点? (2)旋转了多少度? (3)如果连结EF,那么△AEF是怎样的三角形? 参考答案 1.C 2.D 3.解:(1)旋转中心是A点. (2)∵△ABF是由△ADE旋转而成的,∴B是D的对应点, ∴∠DAB就是旋转角,即旋转了90°. (3)∵∠EAF=90°(与旋转角相等)且AF=AE, ∴△AEF是等腰直角三角形. 课堂小结 布置作业 课本第122页练习第1,2,3题. 板书设计 第10章 轴对称、平移与旋转 10.3 旋 转 10.3.2 旋转的特征 旋转的特征: (1)图形中每一点都绕着旋转中心按相同的方向旋转了同样大小的角度. (2)对应点到旋转中心的距离相等. (3)对应线段相等,对应角相等. (4)图形的形状、大小都没有变化,而只改变了位置. 例1 例2 教学反思 教学反思 教学反思 教学反思
