湘教版数学七年级下册 4.3 平行线的性质教案
文档属性
| 名称 | 湘教版数学七年级下册 4.3 平行线的性质教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 100.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 11:09:13 | ||
图片预览

文档简介
4.3 平行线的性质
【教学目标】
知识与技能:经历探索直线平行的性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算.
过程与方法:让学生经历动手操作、发现、猜想、交流、归纳等活动,培养学生的观察能力、操作能力、说理能力和数学语言规范表达能力,在操作中学会与人合作,学会交流自己的思想方法.
情感、态度与价值观:
(1)通过小组讨论,培养合作精神,让学生在探索问题的过程中,体验解决问题的方法和乐趣,增强学习兴趣,在解题中感受生活中数学的存在,体验数学中充满着探索和创造;
(2)培养学生言之有理、言之有据的良好品质,培养学生探索数学问题的兴趣.
【教学重点难点】
重点:探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.
难点:有条理地写出推理过程.
【教学方法】
直观教学法、发现教学法、主体互动法.
【学法引导】
1)教师教法:采用尝试指导、引导发现法,充分发挥学生的主体作用,体现民主意识和开放意识.
2)学生学法:在教师的指导下,积极思维,主动发现,认真研究.
【教学准备】
多媒体教学
【教学过程】
一、情景导入
完成教材86页“做一做”的内容.
问题:根据这些操作,你能猜想出什么结论?
学生:两条平行直线被第三条直线所截,同位角相等.
教师:这个猜想是正确的吗?(引入课题)
二、探究新知
活动1:平行线的性质1
文字简写:两直线平行,同位角相等.
几何表达:,.
课堂练习1
1.如图,a∥b,直线c与a,b都相交.
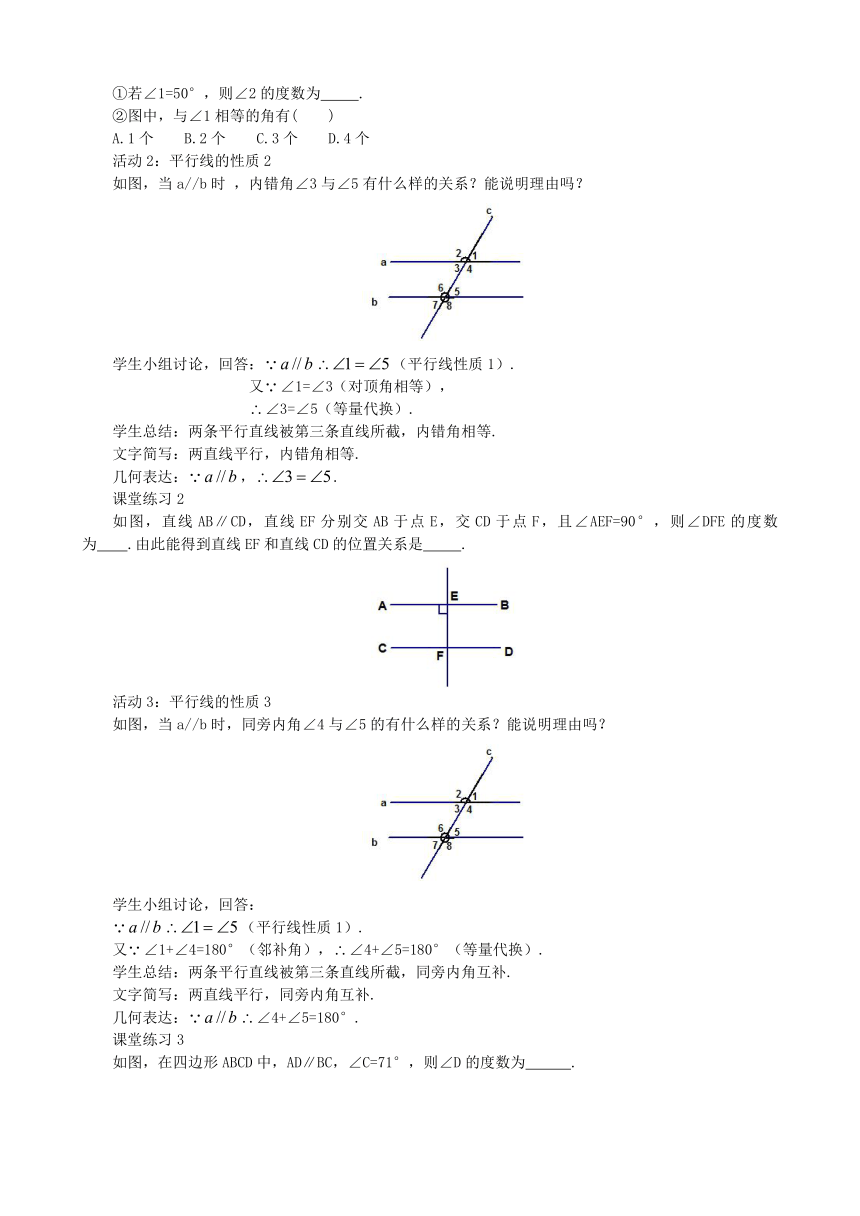
①若∠1=50°,则∠2的度数为 .
②图中,与∠1相等的角有( )
A.1个 B.2个 C.3个 D.4个
活动2:平行线的性质2
如图,当a//b时 ,内错角∠3与∠5有什么样的关系?能说明理由吗?
学生小组讨论,回答:(平行线性质1).
又∠1=∠3(对顶角相等),
∠3=∠5(等量代换).
学生总结:两条平行直线被第三条直线所截,内错角相等.
文字简写:两直线平行,内错角相等.
几何表达:,.
课堂练习2
如图,直线AB∥CD,直线EF分别交AB于点E,交CD于点F,且∠AEF=90°,则∠DFE的度数为 .由此能得到直线EF和直线CD的位置关系是 .
活动3:平行线的性质3
如图,当a//b时,同旁内角∠4与∠5的有什么样的关系?能说明理由吗?
学生小组讨论,回答:
(平行线性质1).
又∠1+∠4=180°(邻补角),∠4+∠5=180°(等量代换).
学生总结:两条平行直线被第三条直线所截,同旁内角互补.
文字简写:两直线平行,同旁内角互补.
几何表达:∠4+∠5=180°.
课堂练习3
如图,在四边形ABCD中,AD∥BC,∠C=71°,则∠D的度数为 .
三、例题解析
例1 如图,直线AB,CD被直线EF所截,AB∥CD,∠1=100°,试求∠3的度数.
解:因为AB∥CD,
所以∠1=∠2= 100°(两直线平行,同位角相等).
又因为∠2 +∠3 = 180°,
所以∠3 = 180°-∠2 = 180°- 100°= 80°.
例2 如图,AD∥BC, ∠B = ∠D,试问∠A与∠C相等吗?为什么?
解:因为AD∥BC,
所以∠A+∠B=180°,
∠D+∠C=180°(两直线平行,同旁内角互补).
又因为∠B =∠D (已知),所以∠A =∠C.
四、巩固练习
1.如图,AB∥CD,CD∥EF,BC∥ED,∠B=70°,求∠C,∠D和∠E的度数.
2. 如图,直线AB,CD被直线AE所截,AB∥CD, ∠1=105°.求∠2,∠3,∠4的度数.
五、课堂小结
(1)本节课你学习到了哪些知识?
(2)还有哪些知识存在问题?
六、布置作业
在例1中,你能分别用平行线的性质2和性质3求出∠3的度数吗?
七、板书设计
【教学目标】
知识与技能:经历探索直线平行的性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算.
过程与方法:让学生经历动手操作、发现、猜想、交流、归纳等活动,培养学生的观察能力、操作能力、说理能力和数学语言规范表达能力,在操作中学会与人合作,学会交流自己的思想方法.
情感、态度与价值观:
(1)通过小组讨论,培养合作精神,让学生在探索问题的过程中,体验解决问题的方法和乐趣,增强学习兴趣,在解题中感受生活中数学的存在,体验数学中充满着探索和创造;
(2)培养学生言之有理、言之有据的良好品质,培养学生探索数学问题的兴趣.
【教学重点难点】
重点:探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.
难点:有条理地写出推理过程.
【教学方法】
直观教学法、发现教学法、主体互动法.
【学法引导】
1)教师教法:采用尝试指导、引导发现法,充分发挥学生的主体作用,体现民主意识和开放意识.
2)学生学法:在教师的指导下,积极思维,主动发现,认真研究.
【教学准备】
多媒体教学
【教学过程】
一、情景导入
完成教材86页“做一做”的内容.
问题:根据这些操作,你能猜想出什么结论?
学生:两条平行直线被第三条直线所截,同位角相等.
教师:这个猜想是正确的吗?(引入课题)
二、探究新知
活动1:平行线的性质1
文字简写:两直线平行,同位角相等.
几何表达:,.
课堂练习1
1.如图,a∥b,直线c与a,b都相交.
①若∠1=50°,则∠2的度数为 .
②图中,与∠1相等的角有( )
A.1个 B.2个 C.3个 D.4个
活动2:平行线的性质2
如图,当a//b时 ,内错角∠3与∠5有什么样的关系?能说明理由吗?
学生小组讨论,回答:(平行线性质1).
又∠1=∠3(对顶角相等),
∠3=∠5(等量代换).
学生总结:两条平行直线被第三条直线所截,内错角相等.
文字简写:两直线平行,内错角相等.
几何表达:,.
课堂练习2
如图,直线AB∥CD,直线EF分别交AB于点E,交CD于点F,且∠AEF=90°,则∠DFE的度数为 .由此能得到直线EF和直线CD的位置关系是 .
活动3:平行线的性质3
如图,当a//b时,同旁内角∠4与∠5的有什么样的关系?能说明理由吗?
学生小组讨论,回答:
(平行线性质1).
又∠1+∠4=180°(邻补角),∠4+∠5=180°(等量代换).
学生总结:两条平行直线被第三条直线所截,同旁内角互补.
文字简写:两直线平行,同旁内角互补.
几何表达:∠4+∠5=180°.
课堂练习3
如图,在四边形ABCD中,AD∥BC,∠C=71°,则∠D的度数为 .
三、例题解析
例1 如图,直线AB,CD被直线EF所截,AB∥CD,∠1=100°,试求∠3的度数.
解:因为AB∥CD,
所以∠1=∠2= 100°(两直线平行,同位角相等).
又因为∠2 +∠3 = 180°,
所以∠3 = 180°-∠2 = 180°- 100°= 80°.
例2 如图,AD∥BC, ∠B = ∠D,试问∠A与∠C相等吗?为什么?
解:因为AD∥BC,
所以∠A+∠B=180°,
∠D+∠C=180°(两直线平行,同旁内角互补).
又因为∠B =∠D (已知),所以∠A =∠C.
四、巩固练习
1.如图,AB∥CD,CD∥EF,BC∥ED,∠B=70°,求∠C,∠D和∠E的度数.
2. 如图,直线AB,CD被直线AE所截,AB∥CD, ∠1=105°.求∠2,∠3,∠4的度数.
五、课堂小结
(1)本节课你学习到了哪些知识?
(2)还有哪些知识存在问题?
六、布置作业
在例1中,你能分别用平行线的性质2和性质3求出∠3的度数吗?
七、板书设计
