人教版数学九年级上册 24.2《点和圆、直线和圆的位置关系》(第1课时)课件(共14张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.2《点和圆、直线和圆的位置关系》(第1课时)课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 11:22:04 | ||
图片预览





文档简介
(共15张PPT)
24.2 点和圆、直线和圆的 位置关系(第1课时)
九年级 上册
点和圆、直线和圆、圆和圆的位置关系是学习圆的重要内容之一,它们都是在学习了圆的有关概念和性质后,进一步研究两个图形之间的位置关系.在研究点和圆的位置关系时,是从其几何特征(交点个数)和代数特性(点到圆心的距离与半径的关系)两个角度刻画的.因此,在与圆有关的位置中,点和圆的位置关系是基础.
对于经过不在同一直线上的三点作圆的问题,可以从过一点、过两点开始探究,其中体现了转化的思想.同时,对过一点、过两点、过不同直线上的三点作圆的探究,其核心都是要明确确定圆的要素——确定圆心和半径.
课件说明
学习目标: 1.理解点和圆的三种位置关系,并会运用它解决一 些实际问题; 2.会过不在同一直线上的三个点作圆,理解三角形
的外心和外接圆的概念; 3.结合本节内容的学习,体会数形结合、分类讨论 的数学思想.
学习重点: 点和圆的位置关系.
课件说明
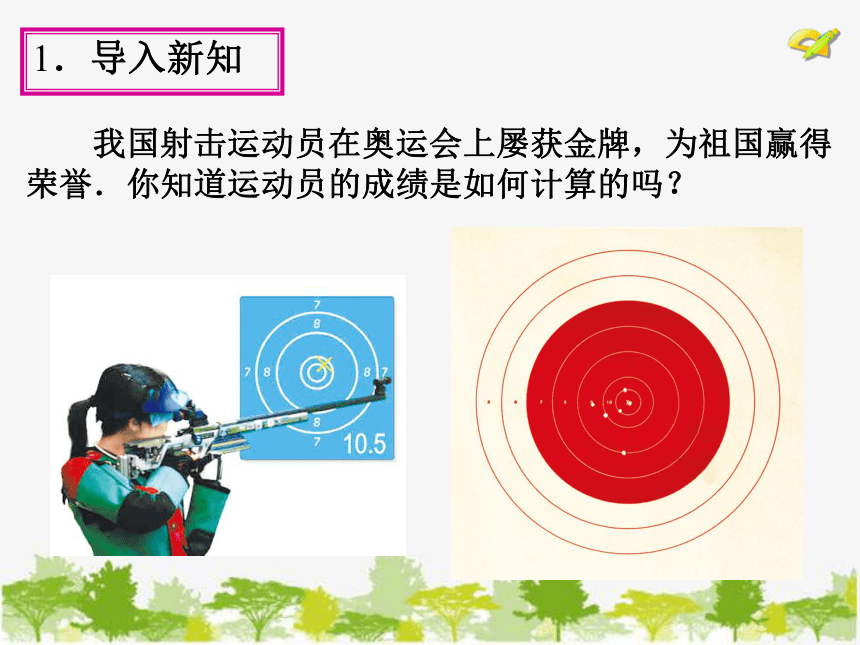
我国射击运动员在奥运会上屡获金牌,为祖国赢得 荣誉.你知道运动员的成绩是如何计算的吗?
1.导入新知
结合上面的问题,你能试着说出点和圆有哪些位置关系吗? 对于点和圆的位置关系,能从数量关系的角度进行 刻画吗? 设⊙O 的半径为 r,点 P 到圆心的距离为 d,则有: 点 P 在圆外 d>r ; 点 P 在圆上 d=r ; 点 P 在圆内 d<r .
2.探究新知
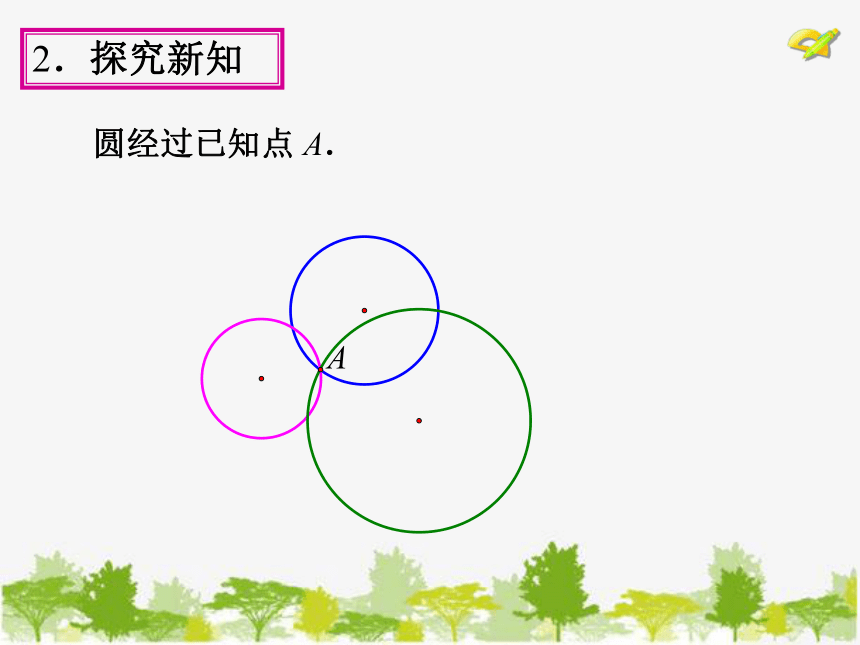
我们知道,已知圆心和半径,可以作一个圆.经过几个已知点,可以作一个圆呢?
2.探究新知
圆经过已知点 A.
2.探究新知
A
圆经过已知点 A、B.
2.探究新知
A
B
已知点 A、B、C
已知三点共线
已知三点不共线
不在同一条直线上的三个点确定一个圆.
2.探究新知
① 连接 AB、BC; ② 分别作线段 AB、BC 的垂直平分线DE 和 FG,DE 和FG 相交于点 O; ③ 以点O 为圆心,OA 为半径作圆,⊙O 就是所要求作的圆.
2.探究新知
O
A
B
C
D
E
F
G
如何经过不在同一条直线上的三个点 A、B、C 作圆?
经过三角形的三个顶点可以作一个圆,这个圆叫做 三角形的外接圆. 外接圆的圆心是三角形三条边的垂直平分线的交点, 叫做这个三角形的外心.
2.探究新知
A
B
C
O
例1 已知⊙O 的半径为 5,圆心 O 的坐标为 (0,0),若点 P 的坐标为(4,2),点 P 与⊙O 的位置关系是( ).
A.点 P 在⊙O 内 B.点 P 在⊙O上
C.点 P 在⊙O 外 D.点 P 在⊙O 上或⊙O 外
3.应用举例
例2 直角三角形的外心是______的中点, 锐角三角形的外心在三角形______,钝角三角形的外心在三角形_________.
(1)点和圆的位置关系:
设⊙O 的半径为 r,点 P 到圆心的距离为 d,则
点 P 在圆外 d>r;
点 P 在圆上 d=r;
点 P 在圆内 d<r.
(2)不在同一条直线上的三个点确定一个圆.
(3)理解三角形外接圆和三角形外心的概念.
4.课堂小结
教科书第 95 页 练习第 2,3 题.
5.布置作业
24.2 点和圆、直线和圆的 位置关系(第1课时)
九年级 上册
点和圆、直线和圆、圆和圆的位置关系是学习圆的重要内容之一,它们都是在学习了圆的有关概念和性质后,进一步研究两个图形之间的位置关系.在研究点和圆的位置关系时,是从其几何特征(交点个数)和代数特性(点到圆心的距离与半径的关系)两个角度刻画的.因此,在与圆有关的位置中,点和圆的位置关系是基础.
对于经过不在同一直线上的三点作圆的问题,可以从过一点、过两点开始探究,其中体现了转化的思想.同时,对过一点、过两点、过不同直线上的三点作圆的探究,其核心都是要明确确定圆的要素——确定圆心和半径.
课件说明
学习目标: 1.理解点和圆的三种位置关系,并会运用它解决一 些实际问题; 2.会过不在同一直线上的三个点作圆,理解三角形
的外心和外接圆的概念; 3.结合本节内容的学习,体会数形结合、分类讨论 的数学思想.
学习重点: 点和圆的位置关系.
课件说明
我国射击运动员在奥运会上屡获金牌,为祖国赢得 荣誉.你知道运动员的成绩是如何计算的吗?
1.导入新知
结合上面的问题,你能试着说出点和圆有哪些位置关系吗? 对于点和圆的位置关系,能从数量关系的角度进行 刻画吗? 设⊙O 的半径为 r,点 P 到圆心的距离为 d,则有: 点 P 在圆外 d>r ; 点 P 在圆上 d=r ; 点 P 在圆内 d<r .
2.探究新知
我们知道,已知圆心和半径,可以作一个圆.经过几个已知点,可以作一个圆呢?
2.探究新知
圆经过已知点 A.
2.探究新知
A
圆经过已知点 A、B.
2.探究新知
A
B
已知点 A、B、C
已知三点共线
已知三点不共线
不在同一条直线上的三个点确定一个圆.
2.探究新知
① 连接 AB、BC; ② 分别作线段 AB、BC 的垂直平分线DE 和 FG,DE 和FG 相交于点 O; ③ 以点O 为圆心,OA 为半径作圆,⊙O 就是所要求作的圆.
2.探究新知
O
A
B
C
D
E
F
G
如何经过不在同一条直线上的三个点 A、B、C 作圆?
经过三角形的三个顶点可以作一个圆,这个圆叫做 三角形的外接圆. 外接圆的圆心是三角形三条边的垂直平分线的交点, 叫做这个三角形的外心.
2.探究新知
A
B
C
O
例1 已知⊙O 的半径为 5,圆心 O 的坐标为 (0,0),若点 P 的坐标为(4,2),点 P 与⊙O 的位置关系是( ).
A.点 P 在⊙O 内 B.点 P 在⊙O上
C.点 P 在⊙O 外 D.点 P 在⊙O 上或⊙O 外
3.应用举例
例2 直角三角形的外心是______的中点, 锐角三角形的外心在三角形______,钝角三角形的外心在三角形_________.
(1)点和圆的位置关系:
设⊙O 的半径为 r,点 P 到圆心的距离为 d,则
点 P 在圆外 d>r;
点 P 在圆上 d=r;
点 P 在圆内 d<r.
(2)不在同一条直线上的三个点确定一个圆.
(3)理解三角形外接圆和三角形外心的概念.
4.课堂小结
教科书第 95 页 练习第 2,3 题.
5.布置作业
同课章节目录
