北师大版数学九年级下册 3.8 圆内接正多边形 同步课时练习:(word版含答案)
文档属性
| 名称 | 北师大版数学九年级下册 3.8 圆内接正多边形 同步课时练习:(word版含答案) | 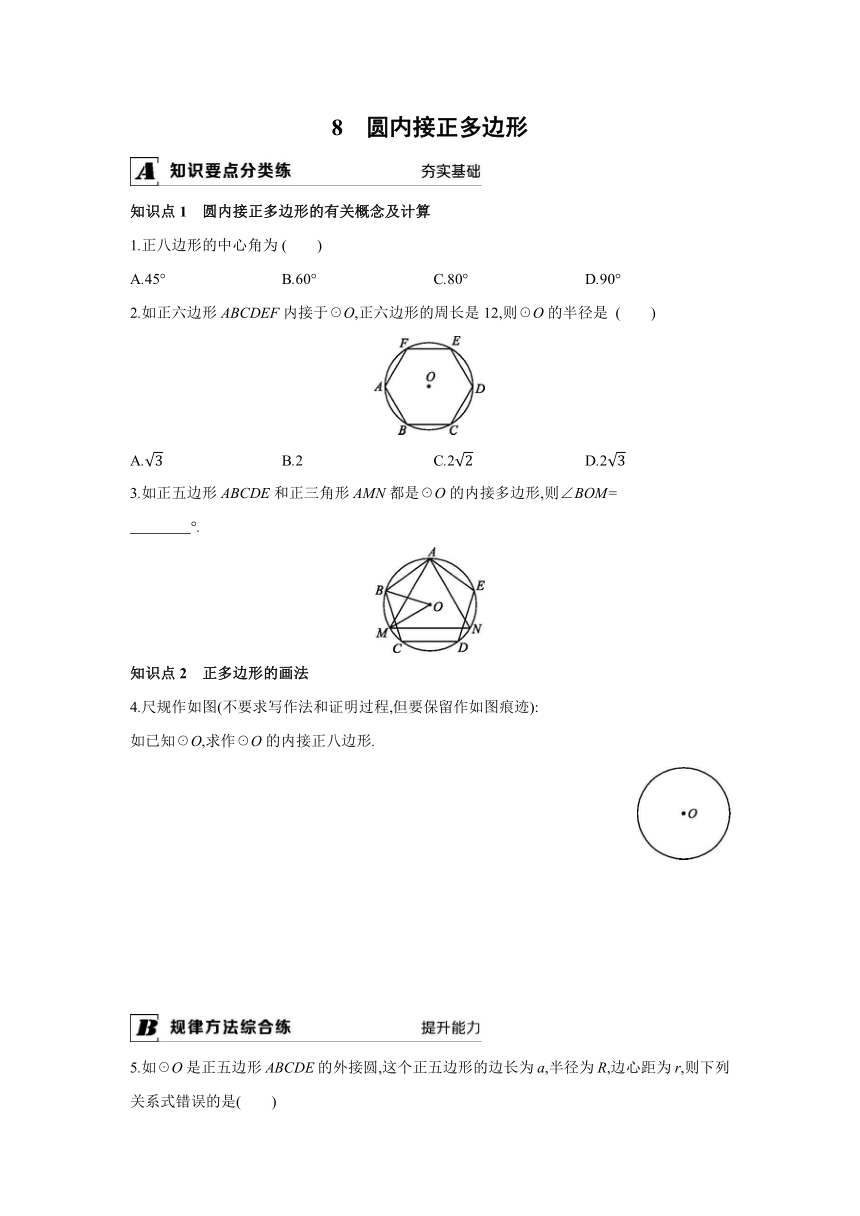 | |
| 格式 | docx | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 08:28:46 | ||
图片预览


文档简介
8 圆内接正多边形
知识点1 圆内接正多边形的有关概念及计算
1.正八边形的中心角为 ( )
A.45° B.60° C.80° D.90°
2.如正六边形ABCDEF内接于☉O,正六边形的周长是12,则☉O的半径是 ( )
A. B.2 C.2 D.2
3.如正五边形ABCDE和正三角形AMN都是☉O的内接多边形,则∠BOM=
°.
知识点2 正多边形的画法
4.尺规作如图(不要求写作法和证明过程,但要保留作如图痕迹):
如已知☉O,求作☉O的内接正八边形.
5.如☉O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2-r2=a2 B.a=2Rsin36°
C.a=2rtan36° D.r=Rcos36°
6.若正六边形的内切圆半径为2,则其外接圆半径为 .
7.如AC是☉O的内接正六边形的一边,点B在上,且BC是☉O的内接正十边形的一边,若AB是☉O的内接正n边形的一边,则n= .
8.如M,N分别是正五边形ABCDE的两边AB,BC上的点,且AM=BN,点O是正五边形的中心,则∠MON的度数是 .
9.如☉O的半径为4cm,点P,Q分别从☉O的内接正六边形ABCDEF的顶点A,D同时出发,均以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,BQ,QE,PE.设运动时间为ts.
(1)求证:四边形PBQE为平行四边形.
(2)填空:
①当t= 时,四边形PBQE为菱形;
②当t= 时,四边形PBQE为矩形.
答案
1.A 2.B
3.48
4.解:如如图,八边形ABCDEFGH就是所求作的正八边形.
5.A
6.
7.15 解:连接BO.
∵AC是☉O的内接正六边形的一边,
∴∠AOC=360°÷6=60°.
∵BC是☉O的内接正十边形的一边,
∴∠BOC=360°÷10=36°,
∴∠AOB=∠AOC-∠BOC=60°-36°=24°,
∴n=360°÷24°=15.
故答案为15.
8.72° 解:如如图,连接OA,OB,OC,则∠AOB==72°.
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC.
在△AOM和△BON中,∵OA=OB,∠OAM=∠OBN,AM=BN,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠MOB+∠BON=∠MOB+∠AOM=∠AOB=72°.
9.解:(1)证明:∵正六边形ABCDEF内接于☉O,
☉O的半径为4cm,∴AB=BC=CD=DE=EF=FA=4cm,∠A=∠ABC=∠C=∠D=∠DEF=∠F.
∵点P,Q分别从A,D两点同时出发,均以1cm/s的速度沿AF,DC向终点F,C运动,
∴AP=DQ=tcm,PF=QC=(4-t)cm.
在△ABP和△DEQ中,
∵AB=DE,∠A=∠D,AP=DQ,
∴△ABP≌△DEQ(SAS),
∴BP=EQ.同理可证PE=QB,
∴四边形PBQE是平行四边形.
(2)①当PA=PF,QC=QD时,四边形PBQE是菱形,此时t=2.故答案为2.
②当t=0时,点P与点A重合,此时可得∠EPF=∠PEF=30°,
∴∠BPE=120°-30°=90°,
∴此时四边形PBQE是矩形.
当t=4时,同理可知∠BPE=90°,此时四边形PBQE是矩形.
综上所述,当t=0或t=4时,四边形PBQE是矩形.故答案为0或4.
知识点1 圆内接正多边形的有关概念及计算
1.正八边形的中心角为 ( )
A.45° B.60° C.80° D.90°
2.如正六边形ABCDEF内接于☉O,正六边形的周长是12,则☉O的半径是 ( )
A. B.2 C.2 D.2
3.如正五边形ABCDE和正三角形AMN都是☉O的内接多边形,则∠BOM=
°.
知识点2 正多边形的画法
4.尺规作如图(不要求写作法和证明过程,但要保留作如图痕迹):
如已知☉O,求作☉O的内接正八边形.
5.如☉O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2-r2=a2 B.a=2Rsin36°
C.a=2rtan36° D.r=Rcos36°
6.若正六边形的内切圆半径为2,则其外接圆半径为 .
7.如AC是☉O的内接正六边形的一边,点B在上,且BC是☉O的内接正十边形的一边,若AB是☉O的内接正n边形的一边,则n= .
8.如M,N分别是正五边形ABCDE的两边AB,BC上的点,且AM=BN,点O是正五边形的中心,则∠MON的度数是 .
9.如☉O的半径为4cm,点P,Q分别从☉O的内接正六边形ABCDEF的顶点A,D同时出发,均以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,BQ,QE,PE.设运动时间为ts.
(1)求证:四边形PBQE为平行四边形.
(2)填空:
①当t= 时,四边形PBQE为菱形;
②当t= 时,四边形PBQE为矩形.
答案
1.A 2.B
3.48
4.解:如如图,八边形ABCDEFGH就是所求作的正八边形.
5.A
6.
7.15 解:连接BO.
∵AC是☉O的内接正六边形的一边,
∴∠AOC=360°÷6=60°.
∵BC是☉O的内接正十边形的一边,
∴∠BOC=360°÷10=36°,
∴∠AOB=∠AOC-∠BOC=60°-36°=24°,
∴n=360°÷24°=15.
故答案为15.
8.72° 解:如如图,连接OA,OB,OC,则∠AOB==72°.
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC.
在△AOM和△BON中,∵OA=OB,∠OAM=∠OBN,AM=BN,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠MOB+∠BON=∠MOB+∠AOM=∠AOB=72°.
9.解:(1)证明:∵正六边形ABCDEF内接于☉O,
☉O的半径为4cm,∴AB=BC=CD=DE=EF=FA=4cm,∠A=∠ABC=∠C=∠D=∠DEF=∠F.
∵点P,Q分别从A,D两点同时出发,均以1cm/s的速度沿AF,DC向终点F,C运动,
∴AP=DQ=tcm,PF=QC=(4-t)cm.
在△ABP和△DEQ中,
∵AB=DE,∠A=∠D,AP=DQ,
∴△ABP≌△DEQ(SAS),
∴BP=EQ.同理可证PE=QB,
∴四边形PBQE是平行四边形.
(2)①当PA=PF,QC=QD时,四边形PBQE是菱形,此时t=2.故答案为2.
②当t=0时,点P与点A重合,此时可得∠EPF=∠PEF=30°,
∴∠BPE=120°-30°=90°,
∴此时四边形PBQE是矩形.
当t=4时,同理可知∠BPE=90°,此时四边形PBQE是矩形.
综上所述,当t=0或t=4时,四边形PBQE是矩形.故答案为0或4.
