北师大版数学九年级下册 第3章 圆 单元测试(word版含解析)
文档属性
| 名称 | 北师大版数学九年级下册 第3章 圆 单元测试(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 210.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 08:38:34 | ||
图片预览




文档简介
第三章 圆 单元测试
一、选择题(每题4分,共28分)
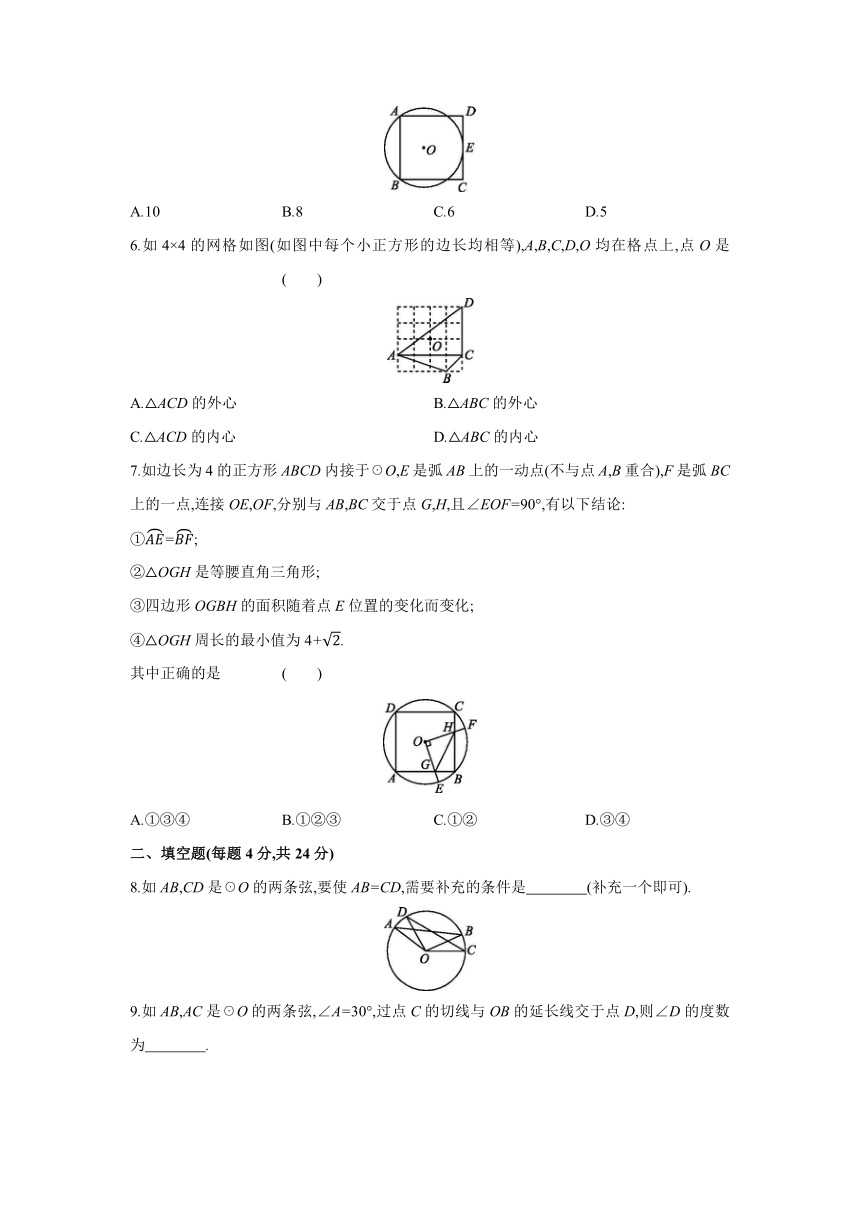
1.已知点P在半径为5cm的☉O内,则点P到圆心O的距离可以是 ( )
A.4cm B.5cm C.6cm D.7cm
2.如PA,PB分别切☉O于点A,B,PA=10,CD切☉O于点E,与PA,PB分别交于点C,D,则△PCD的周长是 ( )
A.10 B.18 C.20 D.22
3.如已知AB是☉O的直径,CD是弦,若∠BCD=36°,则∠ABD等于 ( )
A.54° B.56°
C.64° D.66°
4.如AB是☉O的直径,C,D是☉O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是 ( )
A.OC∥BD
B.AD⊥OC
C.△CEF≌△BED
D.AF=FD
5.如已知☉O的弦AB=8,以AB为一边作正方形ABCD,CD边与☉O相切,切点为E,则☉O的半径为 ( )
A.10 B.8 C.6 D.5
6.如4×4的网格如图(如图中每个小正方形的边长均相等),A,B,C,D,O均在格点上,点O是 ( )
A.△ACD的外心 B.△ABC的外心
C.△ACD的内心 D.△ABC的内心
7.如边长为4的正方形ABCD内接于☉O,E是弧AB上的一动点(不与点A,B重合),F是弧BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
①=;
②△OGH是等腰直角三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△OGH周长的最小值为4+.
其中正确的是 ( )
A.①③④ B.①②③ C.①② D.③④
二、填空题(每题4分,共24分)
8.如AB,CD是☉O的两条弦,要使AB=CD,需要补充的条件是 (补充一个即可).
9.如AB,AC是☉O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为 .
10.直角三角形的两条直角边长分别为6和8,那么这个三角形的外接圆半径为 ,内切圆半径为 .
11.如PA,PB是☉O的切线,A,B为切点,点C,D在☉O上.若∠P=102°,则∠A+∠C=
°.
12.已知半径为2的☉O中,弦AC=2,弦AD=2,则∠COD的度数为 .
13.如,在菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右做无滑动地翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作,菱形中心O所经过的路径总长为 .(结果保留π)
三、解答题(共48分)
14.(10分)如,在☉O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的度数;
(2)已知圆心O到BD的距离为3,求AD的长.
15.(12分)如,AB为☉O的直径,且AB=4,C是上的一动点(不与点A,B重合),过点B作☉O的切线交AC的延长线于点D,E是BD的中点,连接EC.
(1)求证:EC是☉O的切线;
(2)当∠D=30°时,求阴影部分的面积.
16.(12分)如,已知☉O的弦CD与直径AB垂直于点F,点E在CD上,且AE=CE.
(1)求证:CA2=CE·CD;
(2)已知CA=5,AE=3,求sin∠EAF的值.
17.(14分)已知一个零刻度落在点A的量角器(半圆O)的直径为AB,等腰直角三角形BCD绕点B旋转.
(1)如①,当等腰直角三角形BCD运动至斜边BD交量角器边缘于点G,直角边CD交量角器边缘于点E,F,第三边交量角器边缘于点H时,点G在量角器上的读数为20°,求此时点H在量角器上的读数;
(2)如如图②,当点G,E在量角器上的读数α,β满足什么关系时,等腰直角三角形BCD的直角边CD与半圆O相切于点E 请说明理由.
答案
【作者说卷】
圆是同学们非常熟悉的一种几何如图形,系统学习之后我们会发现,其中的知识点多,定理多,公式多,分清它们之间的区别和联系是学好本章知识的关键.本套试卷重点考查这一方面的能力.
知识点分布:(1)圆心角、弧、弦之间的关系及垂径定理,如4,8,14,16题.
(2)圆周角定理及其推论,如9,11,14题.
(3)圆的切线的性质、判定及切线长定理,如2,5,11,15,17题.
(4)点与圆、直线与圆的位置关系,如1题.
(5)弦长、弧长、面积的计算,如13,15题.
思想方法:转化思想、从特殊到一般的思想.
亮点:对有关概念的考查主要通过实例进行,对有关性质的考查更多地关注学生是否借助具体的思想方法去理解,对有关计算着重考查学生是否懂得了基本的定理.
1.A
2.C 解:∵PA,PB分别切☉O于点A,B,CD切☉O于点E,
∴PB=PA=10,CA=CE,DE=DB,
∴△PCD的周长=PC+CD+PD=PC+AC+DB+PD=PA+PB=10+10=20.故选C.
3.A 解:∵AB是☉O的直径,
∴∠ADB=90°.
∵∠DAB=∠BCD=36°,
∴∠ABD=180°-∠ADB-∠DAB=180°-90°-36°=54°.
故选A.
4.C 解:∵AB是☉O的直径,BC平分∠ABD,
∴∠ADB=90°,∠OBC=∠DBC,
∴AD⊥BD.
∵OB=OC,
∴∠OCB=∠OBC,
∴∠DBC=∠OCB,
∴OC∥BD,选项A成立;
∴AD⊥OC,选项B成立;
∴AF=FD,选项D成立;
∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不一定全等,选项C不一定成立.
故选C.
5.D 解:连接EO并延长交AB于点F.
∵CD边与☉O相切,
∴OE⊥CD.
∵四边形ABCD是正方形,
∴AB∥CD,AD=AB=8,
∴EF⊥AB,
∴四边形AFED是矩形,AF=AB=4,
∴EF=AD=8.
连接OA,
∴OA=OE,
∴OF=8-OA.
∵OA2=AF2+OF2,
∴OA2=42+(8-OA)2,
解得OA=5,∴☉O的半径为5.
故选D.
6.B 解:连接OA,OB,OC,OD,设网格中每个小正方形的边长为1.观察如图形可知,OA=OB=OC=,OD=2,
所以点O到A,B,C三点的距离相等,所以点O为△ABC的外心.
故选B.
7.C 解:如如图所示,连接OC,OB,CF,BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴=.
又∵=,∴=,故①正确.
在△BOG与△COH中,
∵∠BOG=∠COH,OB=OC,∠OBG=∠OCH=45°,
∴△BOG≌△COH,
∴OG=OH.
又∵∠HOG=90°,
∴△OGH是等腰直角三角形,故②正确.
∵△BOG≌△COH,
∴S△BOG=S△COH,
∴S四边形OGBH=S△BOC=S正方形ABCD=定值,故③错误.
∵△OGH是等腰直角三角形,
∴当OG⊥BC时,OG的长最小,即△OGH的周长最小,此时OG=OH=2,GH=2,
∴△OGH周长的最小值为4+2,故④错误.故选C.
8.答案不唯一,如=
9.30° 解:连接OC.
∵CD是☉O的切线,
∴∠OCD=90°.
∵∠A=30°,
∴∠BOC=2∠A=60°,
∴∠D=90°-60°=30°.
10.5 2
11.219
12.150°或30°
13.(8+4)π
14.解:(1)∵∠CAB=∠CDB,∠CAB=40°,
∴∠CDB=40°.
又∵∠APD=65°,
∴∠B=65°-40°=25°.
(2)如如图,过点O作OE⊥BD于点E,则OE=3,BE=DE.
又∵O是AB的中点,
∴OE是△ABD的中位线,
∴AD=2OE=6.
15.解:(1)证明:如如图,连接BC,OC,OE.
∵AB为☉O的直径,∴∠ACB=90°.
在Rt△BDC中,∵BE=ED,
∴DE=EC=BE.
又∵OC=OB,OE=OE,
∴△OCE≌△OBE(SSS),
∴∠OCE=∠OBE.
∵BD是☉O的切线,∴∠ABD=90°,
∴∠OCE=∠ABD=90°.
∵OC是☉O的半径,∴EC是☉O的切线.
(2)∵OA=OB,BE=DE,
∴AD∥OE,∴∠D=∠OEB.
∵∠D=30°,∴∠OEB=30°,
∴∠EOB=60°,
∴∠BOC=120°.
∵AB=4,∴OB=2,
∴BE=6,
∴S四边形OBEC=2S△OBE=2××6×2=12,
∴阴影部分的面积为S四边形OBEC-S扇形BOC=12-=12-4π.
16.解:(1)证明:∵弦CD垂直于直径AB,
∴=,
∴∠D=∠C.
∵AE=CE,∴∠CAE=∠C,
∴∠CAE=∠D.
又∵∠C=∠C,
∴△CEA∽△CAD,
∴=,
即CA2=CE·CD.
(2)∵CA2=CE·CD,CA=5,AE=3,AE=CE,
∴52=CD·3,∴CD=.
∵CD⊥AB,∴CF=FD,
∴CF==,
∴EF=CF-CE=-3=.
在Rt△AFE中,sin∠EAF==.
17.解:(1)如如图①所示,连接OG,OH.
∵点G在量角器上的读数为20°,
∴∠AOG=20°.
∵△BCD为等腰直角三角形,
∴∠CBD=45°,∴∠HOG=90°,
∴∠AOH=∠AOG+∠HOG=20°+90°=110°,即点H在量角器上的读数为110°.
(2)β=α+45°.理由如下:
如如图②所示,连接OG,OE.
∵CD为半圆O的切线,E为切点,
∴∠OED=90°,
∴∠OED=∠C,
∴EO∥CB,
∴∠AOE=∠ABC=β.
又∵∠ABG=∠AOG=α,∠ABC=∠ABG+∠DBC,
∴β=α+45°.
一、选择题(每题4分,共28分)
1.已知点P在半径为5cm的☉O内,则点P到圆心O的距离可以是 ( )
A.4cm B.5cm C.6cm D.7cm
2.如PA,PB分别切☉O于点A,B,PA=10,CD切☉O于点E,与PA,PB分别交于点C,D,则△PCD的周长是 ( )
A.10 B.18 C.20 D.22
3.如已知AB是☉O的直径,CD是弦,若∠BCD=36°,则∠ABD等于 ( )
A.54° B.56°
C.64° D.66°
4.如AB是☉O的直径,C,D是☉O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是 ( )
A.OC∥BD
B.AD⊥OC
C.△CEF≌△BED
D.AF=FD
5.如已知☉O的弦AB=8,以AB为一边作正方形ABCD,CD边与☉O相切,切点为E,则☉O的半径为 ( )
A.10 B.8 C.6 D.5
6.如4×4的网格如图(如图中每个小正方形的边长均相等),A,B,C,D,O均在格点上,点O是 ( )
A.△ACD的外心 B.△ABC的外心
C.△ACD的内心 D.△ABC的内心
7.如边长为4的正方形ABCD内接于☉O,E是弧AB上的一动点(不与点A,B重合),F是弧BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
①=;
②△OGH是等腰直角三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△OGH周长的最小值为4+.
其中正确的是 ( )
A.①③④ B.①②③ C.①② D.③④
二、填空题(每题4分,共24分)
8.如AB,CD是☉O的两条弦,要使AB=CD,需要补充的条件是 (补充一个即可).
9.如AB,AC是☉O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为 .
10.直角三角形的两条直角边长分别为6和8,那么这个三角形的外接圆半径为 ,内切圆半径为 .
11.如PA,PB是☉O的切线,A,B为切点,点C,D在☉O上.若∠P=102°,则∠A+∠C=
°.
12.已知半径为2的☉O中,弦AC=2,弦AD=2,则∠COD的度数为 .
13.如,在菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右做无滑动地翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作,菱形中心O所经过的路径总长为 .(结果保留π)
三、解答题(共48分)
14.(10分)如,在☉O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的度数;
(2)已知圆心O到BD的距离为3,求AD的长.
15.(12分)如,AB为☉O的直径,且AB=4,C是上的一动点(不与点A,B重合),过点B作☉O的切线交AC的延长线于点D,E是BD的中点,连接EC.
(1)求证:EC是☉O的切线;
(2)当∠D=30°时,求阴影部分的面积.
16.(12分)如,已知☉O的弦CD与直径AB垂直于点F,点E在CD上,且AE=CE.
(1)求证:CA2=CE·CD;
(2)已知CA=5,AE=3,求sin∠EAF的值.
17.(14分)已知一个零刻度落在点A的量角器(半圆O)的直径为AB,等腰直角三角形BCD绕点B旋转.
(1)如①,当等腰直角三角形BCD运动至斜边BD交量角器边缘于点G,直角边CD交量角器边缘于点E,F,第三边交量角器边缘于点H时,点G在量角器上的读数为20°,求此时点H在量角器上的读数;
(2)如如图②,当点G,E在量角器上的读数α,β满足什么关系时,等腰直角三角形BCD的直角边CD与半圆O相切于点E 请说明理由.
答案
【作者说卷】
圆是同学们非常熟悉的一种几何如图形,系统学习之后我们会发现,其中的知识点多,定理多,公式多,分清它们之间的区别和联系是学好本章知识的关键.本套试卷重点考查这一方面的能力.
知识点分布:(1)圆心角、弧、弦之间的关系及垂径定理,如4,8,14,16题.
(2)圆周角定理及其推论,如9,11,14题.
(3)圆的切线的性质、判定及切线长定理,如2,5,11,15,17题.
(4)点与圆、直线与圆的位置关系,如1题.
(5)弦长、弧长、面积的计算,如13,15题.
思想方法:转化思想、从特殊到一般的思想.
亮点:对有关概念的考查主要通过实例进行,对有关性质的考查更多地关注学生是否借助具体的思想方法去理解,对有关计算着重考查学生是否懂得了基本的定理.
1.A
2.C 解:∵PA,PB分别切☉O于点A,B,CD切☉O于点E,
∴PB=PA=10,CA=CE,DE=DB,
∴△PCD的周长=PC+CD+PD=PC+AC+DB+PD=PA+PB=10+10=20.故选C.
3.A 解:∵AB是☉O的直径,
∴∠ADB=90°.
∵∠DAB=∠BCD=36°,
∴∠ABD=180°-∠ADB-∠DAB=180°-90°-36°=54°.
故选A.
4.C 解:∵AB是☉O的直径,BC平分∠ABD,
∴∠ADB=90°,∠OBC=∠DBC,
∴AD⊥BD.
∵OB=OC,
∴∠OCB=∠OBC,
∴∠DBC=∠OCB,
∴OC∥BD,选项A成立;
∴AD⊥OC,选项B成立;
∴AF=FD,选项D成立;
∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不一定全等,选项C不一定成立.
故选C.
5.D 解:连接EO并延长交AB于点F.
∵CD边与☉O相切,
∴OE⊥CD.
∵四边形ABCD是正方形,
∴AB∥CD,AD=AB=8,
∴EF⊥AB,
∴四边形AFED是矩形,AF=AB=4,
∴EF=AD=8.
连接OA,
∴OA=OE,
∴OF=8-OA.
∵OA2=AF2+OF2,
∴OA2=42+(8-OA)2,
解得OA=5,∴☉O的半径为5.
故选D.
6.B 解:连接OA,OB,OC,OD,设网格中每个小正方形的边长为1.观察如图形可知,OA=OB=OC=,OD=2,
所以点O到A,B,C三点的距离相等,所以点O为△ABC的外心.
故选B.
7.C 解:如如图所示,连接OC,OB,CF,BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴=.
又∵=,∴=,故①正确.
在△BOG与△COH中,
∵∠BOG=∠COH,OB=OC,∠OBG=∠OCH=45°,
∴△BOG≌△COH,
∴OG=OH.
又∵∠HOG=90°,
∴△OGH是等腰直角三角形,故②正确.
∵△BOG≌△COH,
∴S△BOG=S△COH,
∴S四边形OGBH=S△BOC=S正方形ABCD=定值,故③错误.
∵△OGH是等腰直角三角形,
∴当OG⊥BC时,OG的长最小,即△OGH的周长最小,此时OG=OH=2,GH=2,
∴△OGH周长的最小值为4+2,故④错误.故选C.
8.答案不唯一,如=
9.30° 解:连接OC.
∵CD是☉O的切线,
∴∠OCD=90°.
∵∠A=30°,
∴∠BOC=2∠A=60°,
∴∠D=90°-60°=30°.
10.5 2
11.219
12.150°或30°
13.(8+4)π
14.解:(1)∵∠CAB=∠CDB,∠CAB=40°,
∴∠CDB=40°.
又∵∠APD=65°,
∴∠B=65°-40°=25°.
(2)如如图,过点O作OE⊥BD于点E,则OE=3,BE=DE.
又∵O是AB的中点,
∴OE是△ABD的中位线,
∴AD=2OE=6.
15.解:(1)证明:如如图,连接BC,OC,OE.
∵AB为☉O的直径,∴∠ACB=90°.
在Rt△BDC中,∵BE=ED,
∴DE=EC=BE.
又∵OC=OB,OE=OE,
∴△OCE≌△OBE(SSS),
∴∠OCE=∠OBE.
∵BD是☉O的切线,∴∠ABD=90°,
∴∠OCE=∠ABD=90°.
∵OC是☉O的半径,∴EC是☉O的切线.
(2)∵OA=OB,BE=DE,
∴AD∥OE,∴∠D=∠OEB.
∵∠D=30°,∴∠OEB=30°,
∴∠EOB=60°,
∴∠BOC=120°.
∵AB=4,∴OB=2,
∴BE=6,
∴S四边形OBEC=2S△OBE=2××6×2=12,
∴阴影部分的面积为S四边形OBEC-S扇形BOC=12-=12-4π.
16.解:(1)证明:∵弦CD垂直于直径AB,
∴=,
∴∠D=∠C.
∵AE=CE,∴∠CAE=∠C,
∴∠CAE=∠D.
又∵∠C=∠C,
∴△CEA∽△CAD,
∴=,
即CA2=CE·CD.
(2)∵CA2=CE·CD,CA=5,AE=3,AE=CE,
∴52=CD·3,∴CD=.
∵CD⊥AB,∴CF=FD,
∴CF==,
∴EF=CF-CE=-3=.
在Rt△AFE中,sin∠EAF==.
17.解:(1)如如图①所示,连接OG,OH.
∵点G在量角器上的读数为20°,
∴∠AOG=20°.
∵△BCD为等腰直角三角形,
∴∠CBD=45°,∴∠HOG=90°,
∴∠AOH=∠AOG+∠HOG=20°+90°=110°,即点H在量角器上的读数为110°.
(2)β=α+45°.理由如下:
如如图②所示,连接OG,OE.
∵CD为半圆O的切线,E为切点,
∴∠OED=90°,
∴∠OED=∠C,
∴EO∥CB,
∴∠AOE=∠ABC=β.
又∵∠ABG=∠AOG=α,∠ABC=∠ABG+∠DBC,
∴β=α+45°.
