北师大版数学八年级下册同步课时练习:6.3 三角形的中位线 (word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册同步课时练习:6.3 三角形的中位线 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 00:00:00 | ||
图片预览


文档简介
3 三角形的中位线
知识点 1 三角形中位线定理
1.如已知DE是△ABC的中位线,若AC=8,则DE的长为( )
A.2 B.4 C.6 D.8
2.在△ABC中,D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED的度数为
( )
A.22° B.68° C.96° D.112°
3.如在△ABC中,D,E分别是边AB,BC的中点.若△DBE的周长是7,则△ABC的周长是
( )
A.8 B.10 C.12 D.14
4.如在 ABCD中,对角线AC,BD相交于点O,E是AB的中点,OE=5 cm,则AD的长为
cm.
5.如在△ABC中,D,E,F分别为边AB,BC,CA的中点.(1)求证:四边形DECF是平行四边形;(2)若边AC=BC=8,求四边形DECF的周长.
知识点 2 三角形中位线定理的应用
6.如A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选了一点C,连接CA,CB,且分别延长到点M,N,使AM=CA,BN=CB,测得MN=200 m,则A,B间的距离为 m.
7.如示,吴伯伯家有一块等边三角形的空地ABC,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A.15米 B.20米 C.25米 D.30米
知识点 3 中点四边形
8.如在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是 .
9.如在“飞镖形”ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
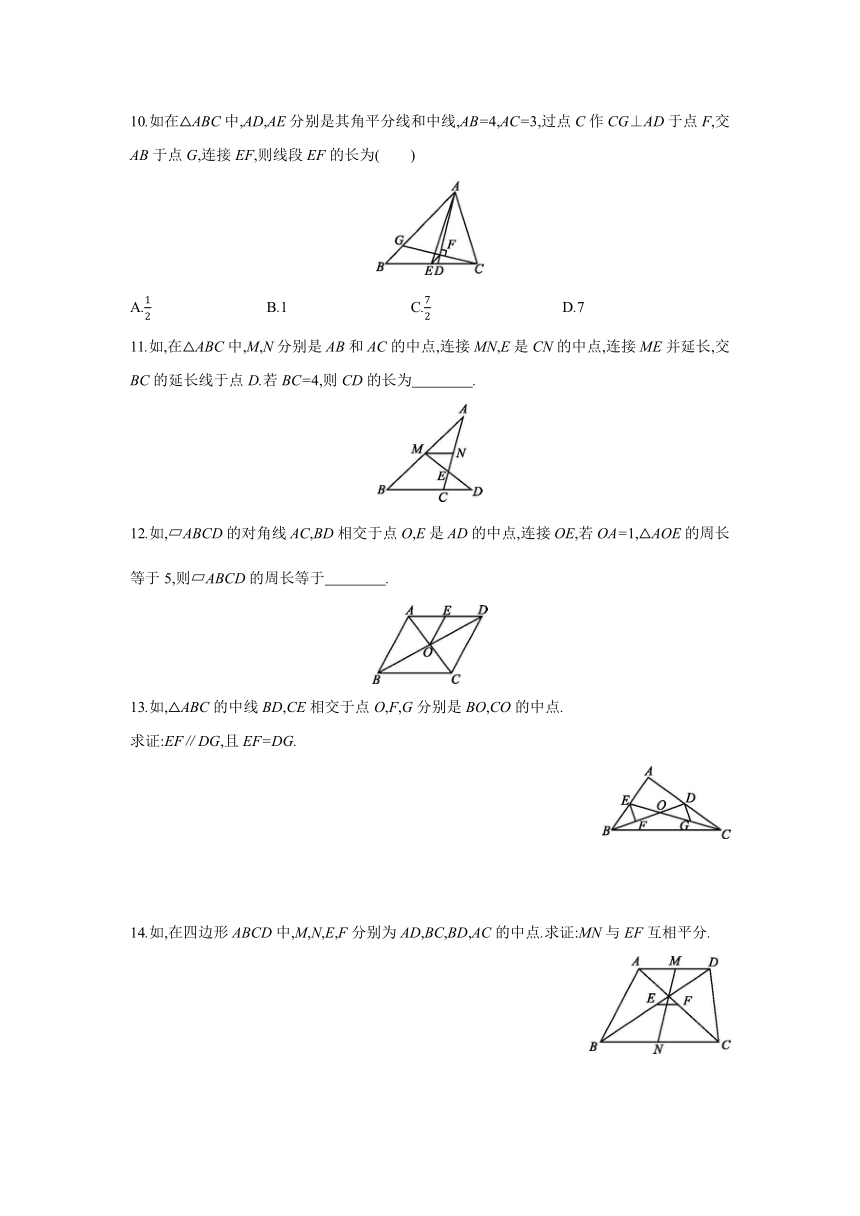
10.如在△ABC中,AD,AE分别是其角平分线和中线,AB=4,AC=3,过点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为( )
A. B.1 C. D.7
11.如,在△ABC中,M,N分别是AB和AC的中点,连接MN,E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 .
12.如, ABCD的对角线AC,BD相交于点O,E是AD的中点,连接OE,若OA=1,△AOE的周长等于5,则 ABCD的周长等于 .
13.如,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点.
求证:EF∥DG,且EF=DG.
14.如,在四边形ABCD中,M,N,E,F分别为AD,BC,BD,AC的中点.求证:MN与EF互相平分.
15.如,在梯形ABCD中,AD∥BC,E,F分别是两腰AB,DC的中点,AF,BC的延长线相交于点G.
(1)求证:△ADF≌△GCF;
(2)类比三角形中位线的定义,我们把EF叫做梯形ABCD的中位线.
阅读填空:
在△ABG中,E是AB的中点,
由(1)的结论可知F是AG的中点,
∴EF是△ABG的 线,
∴EF=BG=(BC+CG).
又由(1)的结论可知:AD=CG,
∴EF=( + ).
因此,可将梯形中位线EF与两底AD,BC的数量关系用文字语言表述为
.
答案
3 三角形的中位线
1.B 解: ∵DE是△ABC的中位线,AC=8,∴DE=AC=×8=4.故选B.
2.B 3.D 4.10
5.解:(1)证明:∵D,F分别是边AB,AC的中点,∴DF∥BC.同理DE∥AC.
∴四边形DECF是平行四边形.
(2)∵AC=BC=8,E,F分别是边BC,AC的中点,∴EC=BC=4,FC=AC=4.∵四边形DECF是平行四边形,∴ DECF的周长=2(EC+FC)=2×(4+4)=16.
6.100
7.C 解: ∵E,F分别是边AB,AC的中点,EF=5米,∴BC=2EF=10米.∵△ABC是等边三角形,∴AB=BC=AC,∴BE=CF=BC=5米,
∴需要篱笆的长=BE+BC+CF+EF=5+10+5+5=25(米).故选C.
8.14
9.证明:连接AC.∵E,F,G,H分别是AB,BC,CD,DA的中点,∴EF,GH分别是△ABC,△ACD的中位线,∴EF∥AC,EF=AC,GH∥AC,GH=AC,∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
10.A 解: 由AD是△ABC的角平分线,CG⊥AD于点F,易证△AFG≌△AFC,∴AG=AC,
CF=FG.∵AB=4,AC=3,∴BG=1.∵AE是△ABC的中线,∴BE=CE,
∴EF为△CBG的中位线,∴EF=BG=.故选A.
11.2 解: 依据三角形中位线定理,即可得到MN=BC=2,MN∥BC,易证△MNE≌△DCE,即可得到CD=MN=2.
12.16 解: ∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OB=OD.又∵E是AD的中点,∴AD=2AE,OE是△ABD的中位线,∴AB=2OE.∵△AOE的周长等于5,∴OA+AE+OE=5,则AE+OE=5-OA=5-1=4,∴AB+AD=2OE+2AE=8,∴ ABCD的周长=2(AB+AD)=2×8=16.
13.证明:如如图, 连接DE,FG.
∵BD,CE是△ABC的中线,∴E,D分别是AB,AC的中点,则DE是△ABC的中位线,
∴DE∥BC,DE=BC.同理FG∥BC,FG=BC,∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,且EF=DG.
14.证明:如如图,连接ME,EN,NF,MF.
∵M,N,E,F分别为AD,BC,BD,AC的中点,
∴ME∥AB且ME=AB,NF∥AB且NF=AB,∴ME∥NF且ME=NF,
∴四边形MENF是平行四边形,
∴MN与EF互相平分.
15.解:(1)证明:∵AD∥BC,
∴∠ADF=∠GCF.
∵F为DC的中点,
∴DF=CF.
在△ADF和△GCF中,
∵∠ADF=∠GCF,DF=CF,∠AFD=∠GFC,
∴△ADF≌△GCF(ASA).
(2)中位 BC AD 梯形的中位线等于两底和的一半
知识点 1 三角形中位线定理
1.如已知DE是△ABC的中位线,若AC=8,则DE的长为( )
A.2 B.4 C.6 D.8
2.在△ABC中,D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED的度数为
( )
A.22° B.68° C.96° D.112°
3.如在△ABC中,D,E分别是边AB,BC的中点.若△DBE的周长是7,则△ABC的周长是
( )
A.8 B.10 C.12 D.14
4.如在 ABCD中,对角线AC,BD相交于点O,E是AB的中点,OE=5 cm,则AD的长为
cm.
5.如在△ABC中,D,E,F分别为边AB,BC,CA的中点.(1)求证:四边形DECF是平行四边形;(2)若边AC=BC=8,求四边形DECF的周长.
知识点 2 三角形中位线定理的应用
6.如A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选了一点C,连接CA,CB,且分别延长到点M,N,使AM=CA,BN=CB,测得MN=200 m,则A,B间的距离为 m.
7.如示,吴伯伯家有一块等边三角形的空地ABC,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A.15米 B.20米 C.25米 D.30米
知识点 3 中点四边形
8.如在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是 .
9.如在“飞镖形”ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
10.如在△ABC中,AD,AE分别是其角平分线和中线,AB=4,AC=3,过点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为( )
A. B.1 C. D.7
11.如,在△ABC中,M,N分别是AB和AC的中点,连接MN,E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 .
12.如, ABCD的对角线AC,BD相交于点O,E是AD的中点,连接OE,若OA=1,△AOE的周长等于5,则 ABCD的周长等于 .
13.如,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点.
求证:EF∥DG,且EF=DG.
14.如,在四边形ABCD中,M,N,E,F分别为AD,BC,BD,AC的中点.求证:MN与EF互相平分.
15.如,在梯形ABCD中,AD∥BC,E,F分别是两腰AB,DC的中点,AF,BC的延长线相交于点G.
(1)求证:△ADF≌△GCF;
(2)类比三角形中位线的定义,我们把EF叫做梯形ABCD的中位线.
阅读填空:
在△ABG中,E是AB的中点,
由(1)的结论可知F是AG的中点,
∴EF是△ABG的 线,
∴EF=BG=(BC+CG).
又由(1)的结论可知:AD=CG,
∴EF=( + ).
因此,可将梯形中位线EF与两底AD,BC的数量关系用文字语言表述为
.
答案
3 三角形的中位线
1.B 解: ∵DE是△ABC的中位线,AC=8,∴DE=AC=×8=4.故选B.
2.B 3.D 4.10
5.解:(1)证明:∵D,F分别是边AB,AC的中点,∴DF∥BC.同理DE∥AC.
∴四边形DECF是平行四边形.
(2)∵AC=BC=8,E,F分别是边BC,AC的中点,∴EC=BC=4,FC=AC=4.∵四边形DECF是平行四边形,∴ DECF的周长=2(EC+FC)=2×(4+4)=16.
6.100
7.C 解: ∵E,F分别是边AB,AC的中点,EF=5米,∴BC=2EF=10米.∵△ABC是等边三角形,∴AB=BC=AC,∴BE=CF=BC=5米,
∴需要篱笆的长=BE+BC+CF+EF=5+10+5+5=25(米).故选C.
8.14
9.证明:连接AC.∵E,F,G,H分别是AB,BC,CD,DA的中点,∴EF,GH分别是△ABC,△ACD的中位线,∴EF∥AC,EF=AC,GH∥AC,GH=AC,∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
10.A 解: 由AD是△ABC的角平分线,CG⊥AD于点F,易证△AFG≌△AFC,∴AG=AC,
CF=FG.∵AB=4,AC=3,∴BG=1.∵AE是△ABC的中线,∴BE=CE,
∴EF为△CBG的中位线,∴EF=BG=.故选A.
11.2 解: 依据三角形中位线定理,即可得到MN=BC=2,MN∥BC,易证△MNE≌△DCE,即可得到CD=MN=2.
12.16 解: ∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OB=OD.又∵E是AD的中点,∴AD=2AE,OE是△ABD的中位线,∴AB=2OE.∵△AOE的周长等于5,∴OA+AE+OE=5,则AE+OE=5-OA=5-1=4,∴AB+AD=2OE+2AE=8,∴ ABCD的周长=2(AB+AD)=2×8=16.
13.证明:如如图, 连接DE,FG.
∵BD,CE是△ABC的中线,∴E,D分别是AB,AC的中点,则DE是△ABC的中位线,
∴DE∥BC,DE=BC.同理FG∥BC,FG=BC,∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,且EF=DG.
14.证明:如如图,连接ME,EN,NF,MF.
∵M,N,E,F分别为AD,BC,BD,AC的中点,
∴ME∥AB且ME=AB,NF∥AB且NF=AB,∴ME∥NF且ME=NF,
∴四边形MENF是平行四边形,
∴MN与EF互相平分.
15.解:(1)证明:∵AD∥BC,
∴∠ADF=∠GCF.
∵F为DC的中点,
∴DF=CF.
在△ADF和△GCF中,
∵∠ADF=∠GCF,DF=CF,∠AFD=∠GFC,
∴△ADF≌△GCF(ASA).
(2)中位 BC AD 梯形的中位线等于两底和的一半
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
