北师大版数学八年级下册同步课时练习:第六章 平行四边形 单元测试 (word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册同步课时练习:第六章 平行四边形 单元测试 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 09:22:01 | ||
图片预览


文档简介
第六章 平行四边形
一、选择题(每题5分,共30分)
1.若一个正多边形的内角和为720°,则这个正多边形的边数是( )
A.4 B.5 C.6 D.7
2.如在Rt△ABC中,∠C=90°,∠A=30°,BC=1,D,E分别是直角边BC,AC的中点,则DE的长为( )
A.1 B.2 C. D.1+
3.如在 ABCD中,AP和BP分别平分∠DAB和∠CBA.点P在边DC上.若AD=4 cm,AP=6 cm,则△ABP的面积等于( )
A.30 cm2 B.6 cm2 C.24 cm2 D.12 cm2
4.已知一个四边形的边长顺次为a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则此四边形是( )
A.任意四边形 B.平行四边形
C.对角线相等的平行四边形 D.对角线互相垂直的平行四边形
5.如在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的所有 ADCE中,DE的最小值是( )
A.2 B.4 C.6 D.8
6.如在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以每秒3个单位长度的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒1个单位长度的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动的时间为( )
A.4 s B.3 s C.2 s D.1 s
二、填空题(每题6分,共24分)
7.在 ABCD中,若∠A+∠C=100°,则∠B= °.
8.如在 ABCD中,AB,BC的长分别为12和24,边AD与BC之间的距离为5,则AB与CD之间的距离为 .
9.如在 ABCD中,对角线AC,BD相交于点O,BD⊥AB.若AB=3,BC=5,则AC的长是 .
10.如已知坐标原点O为 ABCD的对角线AC的中点,顶点A的横坐标为4,AD平行于x轴,且AD的长为5.若 ABCD的面积为10,则顶点B的坐标为 .
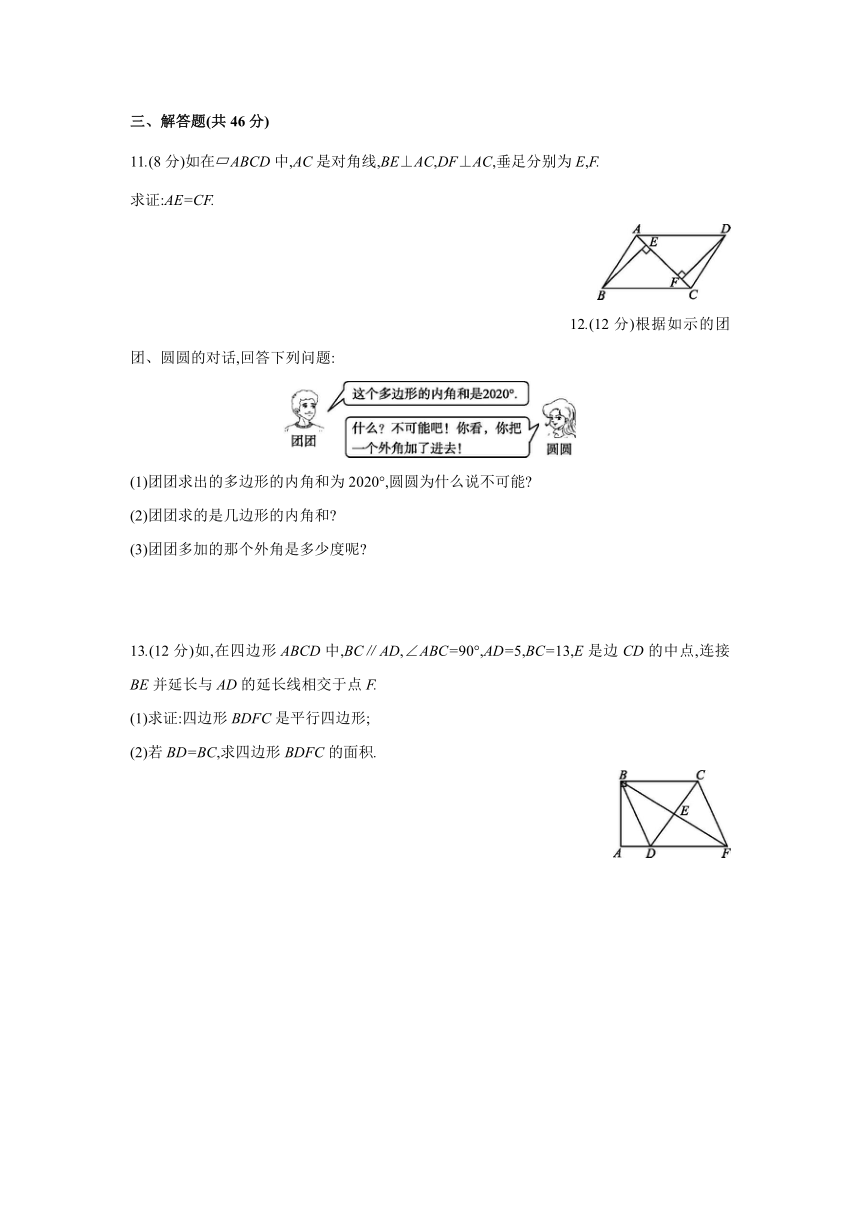
三、解答题(共46分)
11.(8分)如在 ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.
求证:AE=CF.
12.(12分)根据如示的团团、圆圆的对话,回答下列问题:
(1)团团求出的多边形的内角和为2020°,圆圆为什么说不可能
(2)团团求的是几边形的内角和
(3)团团多加的那个外角是多少度呢
13.(12分)如,在四边形ABCD中,BC∥AD,∠ABC=90°,AD=5,BC=13,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若BD=BC,求四边形BDFC的面积.
14.(14分)如,在 ABCD中,E为BC边上的一个动点(不与点B,C重合),过点E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G.
(1)若E为BC的中点,求证:BF=CG.
(2)若AB=5,BC=10,∠B=60°,当点E在线段BC上运动时,FG的长度是否改变 若不变,求出FG的长;若改变,请说明理由.
答案
自我综合评价(六)
1.C 2.A 3.B
4.B 解: 根据a2+b2+c2+d2=2ac+2bd,整理得(a-c)2+(b-d)2=0,那么a=c,b=d,所以此四边形是平行四边形.故选B.
5.B
6.B 解: 若四边形PQBC为平行四边形,则点P在DC上,此时,设运动时间为t s,则CP=12-3t,BQ=t,根据题意,得12-3t=t,解得t=3.故选B.
7.130 解: ∵四边形ABCD为平行四边形,
∴∠A=∠C.又∠A+∠C=100°,∴∠A=∠C=50°.又∵AD∥BC,∴∠B=180°-∠A=180°-50°=130°.
8.10 解: 如如图,过点A作AE⊥BC于点E,AF⊥CD于点F.
由题意,得S ABCD=AE·BC=CD·AF,∴24×5=12·AF,∴AF=10,即AB与CD之间的距离为10.
9.2
10.(1,-1) 解: 如如图,连接BD,设AD与y轴交于点M.
∵点A的横坐标为4,AD平行于x轴,且AD的长为5,
∴点D的横坐标为-1.
∵ ABCD的面积为10,
∴AD·OM=×10,
∴OM=1,
∴点D(-1,1).
∵四边形ABCD是平行四边形,坐标原点O为 ABCD的对角线AC的中点,
∴点B与点D关于原点O中心对称,
∴点B(1,-1).
故答案为(1,-1).
11.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF.
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,∵∠AEB=∠CFD,∠BAE=∠DCF,AB=CD,
∴△ABE≌△CDF,∴AE=CF.
12.解:(1)假设n边形的内角和为2020°,则有(n-2)·180°=2020°,解得n=13.因为边数不能是分数,所以n不存在,所以圆圆说不可能.
(2)团团求的是十三边形的内角和.
(3)团团多加的那个外角是2020°-(13-2)×180°=40°.
13.解:(1)证明:∵BC∥AF,
∴∠CBE=∠DFE.
∵E是边CD的中点,∴CE=DE.
在△BEC与△FED中,∵∠CBE=∠DFE,∠BEC=∠FED,CE=DE,
∴△BEC≌△FED(AAS),
∴BE=FE.
又∵CE=DE,
∴四边形BDFC是平行四边形.
(2)由(1)得△BEC≌△FED,
∴DF=BC=13.
∵BC∥AD,∴∠BAD+∠ABC=180°,
∴∠BAD=180°-∠ABC=180°-90°=90°.
∵BD=BC=13,AD=5,
∴AB===12,
∴四边形BDFC的面积=DF·AB=13×12=156.
14.解:(1)证明:∵四边形ABCD是平行四边形,
∴BF∥CG,∴∠BFE=∠G.
∵E为BC的中点,
∴BE=CE,
又∵∠BEF=∠CEG,
∴△BEF≌△CEG(AAS),
∴BF=CG.
(2)FG的长度不变.
如如图,取BC的中点J,连接AC,AJ.
∵BC=10,∴BJ=CJ=BC=5=AB.
又∵∠B=60°,
∴△ABJ是等边三角形,
∴AJ=BJ=CJ=5,
易得∠BAC=90°,
∴AC===5.
∵EF⊥AB,
∴∠BAC=∠BFE=90°,
∴AC∥FG.
又∵AF∥CG,
∴四边形AFGC是平行四边形,
∴FG=AC=5.
一、选择题(每题5分,共30分)
1.若一个正多边形的内角和为720°,则这个正多边形的边数是( )
A.4 B.5 C.6 D.7
2.如在Rt△ABC中,∠C=90°,∠A=30°,BC=1,D,E分别是直角边BC,AC的中点,则DE的长为( )
A.1 B.2 C. D.1+
3.如在 ABCD中,AP和BP分别平分∠DAB和∠CBA.点P在边DC上.若AD=4 cm,AP=6 cm,则△ABP的面积等于( )
A.30 cm2 B.6 cm2 C.24 cm2 D.12 cm2
4.已知一个四边形的边长顺次为a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则此四边形是( )
A.任意四边形 B.平行四边形
C.对角线相等的平行四边形 D.对角线互相垂直的平行四边形
5.如在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的所有 ADCE中,DE的最小值是( )
A.2 B.4 C.6 D.8
6.如在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以每秒3个单位长度的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒1个单位长度的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动的时间为( )
A.4 s B.3 s C.2 s D.1 s
二、填空题(每题6分,共24分)
7.在 ABCD中,若∠A+∠C=100°,则∠B= °.
8.如在 ABCD中,AB,BC的长分别为12和24,边AD与BC之间的距离为5,则AB与CD之间的距离为 .
9.如在 ABCD中,对角线AC,BD相交于点O,BD⊥AB.若AB=3,BC=5,则AC的长是 .
10.如已知坐标原点O为 ABCD的对角线AC的中点,顶点A的横坐标为4,AD平行于x轴,且AD的长为5.若 ABCD的面积为10,则顶点B的坐标为 .
三、解答题(共46分)
11.(8分)如在 ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.
求证:AE=CF.
12.(12分)根据如示的团团、圆圆的对话,回答下列问题:
(1)团团求出的多边形的内角和为2020°,圆圆为什么说不可能
(2)团团求的是几边形的内角和
(3)团团多加的那个外角是多少度呢
13.(12分)如,在四边形ABCD中,BC∥AD,∠ABC=90°,AD=5,BC=13,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若BD=BC,求四边形BDFC的面积.
14.(14分)如,在 ABCD中,E为BC边上的一个动点(不与点B,C重合),过点E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G.
(1)若E为BC的中点,求证:BF=CG.
(2)若AB=5,BC=10,∠B=60°,当点E在线段BC上运动时,FG的长度是否改变 若不变,求出FG的长;若改变,请说明理由.
答案
自我综合评价(六)
1.C 2.A 3.B
4.B 解: 根据a2+b2+c2+d2=2ac+2bd,整理得(a-c)2+(b-d)2=0,那么a=c,b=d,所以此四边形是平行四边形.故选B.
5.B
6.B 解: 若四边形PQBC为平行四边形,则点P在DC上,此时,设运动时间为t s,则CP=12-3t,BQ=t,根据题意,得12-3t=t,解得t=3.故选B.
7.130 解: ∵四边形ABCD为平行四边形,
∴∠A=∠C.又∠A+∠C=100°,∴∠A=∠C=50°.又∵AD∥BC,∴∠B=180°-∠A=180°-50°=130°.
8.10 解: 如如图,过点A作AE⊥BC于点E,AF⊥CD于点F.
由题意,得S ABCD=AE·BC=CD·AF,∴24×5=12·AF,∴AF=10,即AB与CD之间的距离为10.
9.2
10.(1,-1) 解: 如如图,连接BD,设AD与y轴交于点M.
∵点A的横坐标为4,AD平行于x轴,且AD的长为5,
∴点D的横坐标为-1.
∵ ABCD的面积为10,
∴AD·OM=×10,
∴OM=1,
∴点D(-1,1).
∵四边形ABCD是平行四边形,坐标原点O为 ABCD的对角线AC的中点,
∴点B与点D关于原点O中心对称,
∴点B(1,-1).
故答案为(1,-1).
11.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF.
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,∵∠AEB=∠CFD,∠BAE=∠DCF,AB=CD,
∴△ABE≌△CDF,∴AE=CF.
12.解:(1)假设n边形的内角和为2020°,则有(n-2)·180°=2020°,解得n=13.因为边数不能是分数,所以n不存在,所以圆圆说不可能.
(2)团团求的是十三边形的内角和.
(3)团团多加的那个外角是2020°-(13-2)×180°=40°.
13.解:(1)证明:∵BC∥AF,
∴∠CBE=∠DFE.
∵E是边CD的中点,∴CE=DE.
在△BEC与△FED中,∵∠CBE=∠DFE,∠BEC=∠FED,CE=DE,
∴△BEC≌△FED(AAS),
∴BE=FE.
又∵CE=DE,
∴四边形BDFC是平行四边形.
(2)由(1)得△BEC≌△FED,
∴DF=BC=13.
∵BC∥AD,∴∠BAD+∠ABC=180°,
∴∠BAD=180°-∠ABC=180°-90°=90°.
∵BD=BC=13,AD=5,
∴AB===12,
∴四边形BDFC的面积=DF·AB=13×12=156.
14.解:(1)证明:∵四边形ABCD是平行四边形,
∴BF∥CG,∴∠BFE=∠G.
∵E为BC的中点,
∴BE=CE,
又∵∠BEF=∠CEG,
∴△BEF≌△CEG(AAS),
∴BF=CG.
(2)FG的长度不变.
如如图,取BC的中点J,连接AC,AJ.
∵BC=10,∴BJ=CJ=BC=5=AB.
又∵∠B=60°,
∴△ABJ是等边三角形,
∴AJ=BJ=CJ=5,
易得∠BAC=90°,
∴AC===5.
∵EF⊥AB,
∴∠BAC=∠BFE=90°,
∴AC∥FG.
又∵AF∥CG,
∴四边形AFGC是平行四边形,
∴FG=AC=5.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
