北师大版数学八年级下册同步课时练习:第三章 如图形的平移与旋转 单元测试 (word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册同步课时练习:第三章 如图形的平移与旋转 单元测试 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 218.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 00:00:00 | ||
图片预览


文档简介
第三章 如图形的平移与旋转
一、选择题(每题6分,共36分)
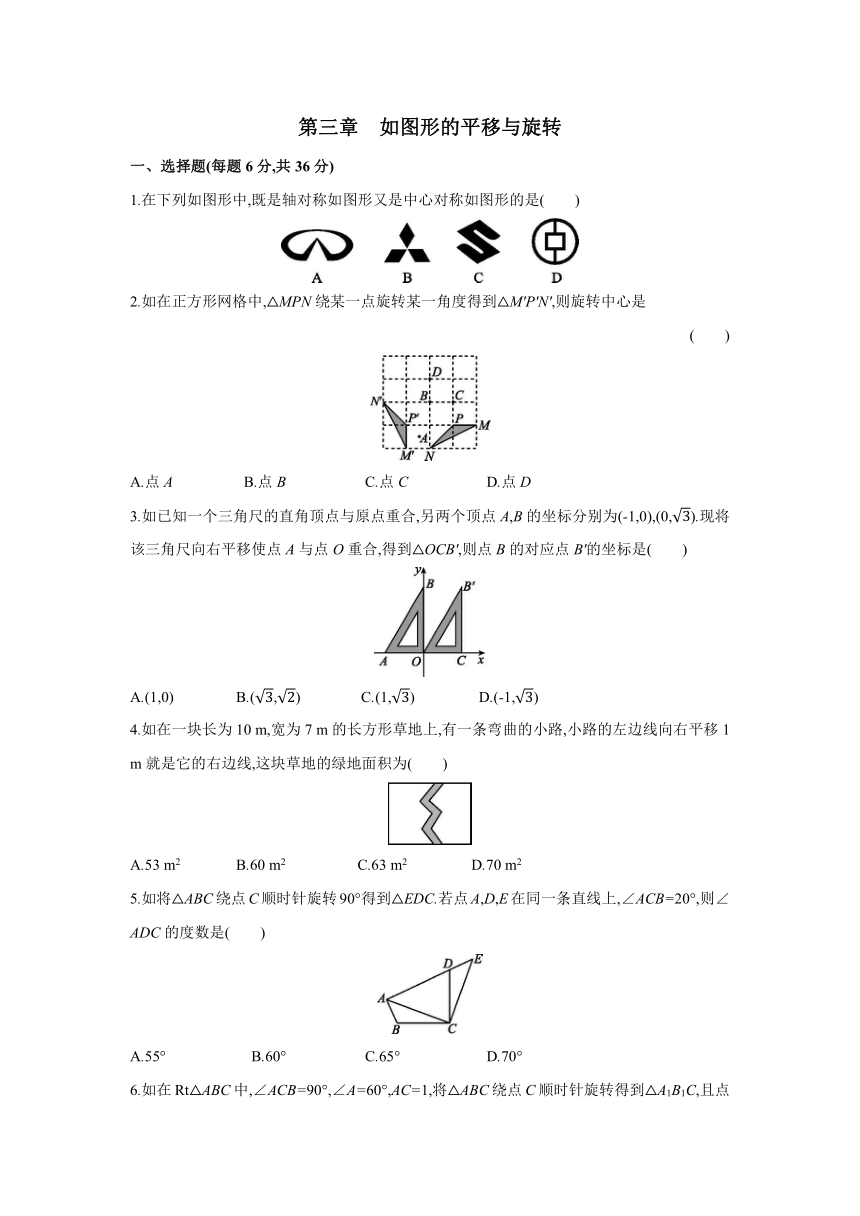
1.在下列如图形中,既是轴对称如图形又是中心对称如图形的是( )
2.如在正方形网格中,△MPN绕某一点旋转某一角度得到△M'P'N',则旋转中心是
( )
A.点A B.点B C.点C D.点D
3.如已知一个三角尺的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角尺向右平移使点A与点O重合,得到△OCB',则点B的对应点B'的坐标是( )
A.(1,0) B.(,) C.(1,) D.(-1,)
4.如在一块长为10 m,宽为7 m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1 m就是它的右边线,这块草地的绿地面积为( )
A.53 m2 B.60 m2 C.63 m2 D.70 m2
5.如将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55° B.60° C.65° D.70°
6.如在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得到△A1B1C,且点A1落在边AB上,取BB1的中点D,连接CD,则CD的长为( )
A. B. C.2 D.3
二、填空题(每题6分,共24分)
7.在平面直角坐标系中,将△ABC向右平移4个单位长度得到△A1B1C1,再将△A1B1C1向上平移3个单位长度得到△A2B2C2,若将△A2B2C2看成是由△ABC经过一次平移得到的,则平移的距离是 个单位长度.
8.如△ABC和△AB'C'成中心对称,点A为对称中心,若∠C=90°,∠B=30°,BC=,则BB'的长为 .
9.如将等边三角形ABC沿BC方向平移得到△A1B1C1,A1B1与AC交于点P.若BC=3,=,则BB1= .
10.如△ABC是边长为4 cm的等边三角形,点D在AB边上(不与点A,B重合),将△ACD绕点C按逆时针方向旋转60°得到△BCE,连接DE,则△BDE周长的最小值是 cm.
三、解答题(共40分)
11.(13分)如,在平面直角坐标系中,有一Rt△ABC,且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
(1)旋转中心的坐标是 ,旋转角的度数是 ;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°,180°得到的三角形;
(3)利用变换前后所形成的如图案,可以证明的定理是 .
12.(13分)如,在△ABC中,AD平分∠BAC交BC于点D.
(1)如如图①,将△ABD沿BC方向平移,使点D移至点C的位置,得到△A'B'D',且A'B'交AC于点E,猜想∠B'EC与∠A'之间的数量关系,并说明理由;(2)如如图②,将△ABD沿AC方向平移,使AB的对应边A'B'经过点D,得到△A'B'D'.求证:A'D'平分∠B'A'C.
13.(14分)如①所示,△ABC,△ECD都是等边三角形,点E在BC上.
(1)试确定AE,BD之间的大小关系;
(2)如果把△ECD绕点C按逆时针方向旋转到如如图②所示的位置,那么(1)中的结论还成立吗 请说明理由.
答案
自我综合评价(三)
1.D 2.B
3.C 解: 因为点A与点O对应,点A(-1,0),点O(0,0),所以如图形向右平移1个单位长度,所以点B的对应点B'的坐标为(0+1,),即(1,).
4.C 解: (10-1)×7=9×7=63(m2).
故这块草地的绿地面积为63 m2.
故选C.
5.C 解: ∵将△ABC绕点C顺时针旋转90°得到△EDC,
∴∠DCE=∠ACB=20°,∠ACE=90°,AC=CE,∴∠ACD=90°-20°=70°.
∵点A,D,E在同一条直线上,∠ACE=90°,AC=CE,∴∠DAC=45°.
在△ADC中,∠ADC+∠DAC+∠ACD=180°,即∠ADC+45°+70°=180°,解得∠ADC=65°.
6.A
7.5 解: 平移的距离是=5(个)单位长度.
8.4
9.1 解: 过点P作PD⊥B1C于点D.
∵将等边三角形ABC沿BC方向平移得到△A1B1C1,∴∠PB1C=∠B=∠ACB=60°,
∴∠CPB1=60°,∴△PCB1是等边三角形.
设等边三角形PCB1的边长是2a,则B1D=CD=a,由勾股定理得PD=a.
∵=,∴·2a·a=,解得a=1(负值已舍去),
∴B1C=2,∴BB1=3-2=1.故答案为1.
10.(4+2) 解: ∵将△ACD绕点C按逆时针方向旋转60°得到△BCE,∴AD=BE,∠DCE=60°,CD=CE,∴△CDE是等边三角形,∴CD=DE,∴△BDE的周长=BD+BE+DE=BD+AD+CD=AB+CD=4+CD,∴当CD取最小值时,△BDE的周长有最小值.∵当CD⊥AB时,CD有最小值为2,∴△BDE周长的最小值为(4+2)cm.
11.解:(1)(0,0) 90°
(2)如如图,△A1AC1顺时针旋转90°,180°得到的三角形分别是△A2A1C2,△BA2C3.
(3)勾股定理
12.解:(1)∠B'EC=2∠A'.理由如下:∵△A'B'D'是由△ABD平移所得,
∴A'B'∥AB,∠A'=∠BAD,∴∠B'EC=∠BAC.∵AD平分∠BAC,∴∠BAC=2∠BAD,
∴∠B'EC=2∠A'.
(2)证明:∵△A'B'D'是由△ABD平移所得,∴A'B'∥AB,∠B'A'D'=∠BAD,
∴∠B'A'C=∠BAC.∵AD平分∠BAC,∴∠BAC=2∠BAD,
∴∠B'A'C=2∠B'A'D',∴A'D'平分∠B'A'C.
13.解:(1)∵△ABC和△ECD都是等边三角形,∴AC=BC,∠ACB=∠ECD=60°,CE=CD,
∴△ACE≌△BCD,∴AE=BD.
(2)成立.理由如下:由(1)知AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACE=∠BCD.在△ACE和△BCD中,
∵AC=BC,∠ACE=∠BCD,CE=CD,
∴△ACE≌△BCD,
∴AE=BD.
一、选择题(每题6分,共36分)
1.在下列如图形中,既是轴对称如图形又是中心对称如图形的是( )
2.如在正方形网格中,△MPN绕某一点旋转某一角度得到△M'P'N',则旋转中心是
( )
A.点A B.点B C.点C D.点D
3.如已知一个三角尺的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角尺向右平移使点A与点O重合,得到△OCB',则点B的对应点B'的坐标是( )
A.(1,0) B.(,) C.(1,) D.(-1,)
4.如在一块长为10 m,宽为7 m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1 m就是它的右边线,这块草地的绿地面积为( )
A.53 m2 B.60 m2 C.63 m2 D.70 m2
5.如将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55° B.60° C.65° D.70°
6.如在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得到△A1B1C,且点A1落在边AB上,取BB1的中点D,连接CD,则CD的长为( )
A. B. C.2 D.3
二、填空题(每题6分,共24分)
7.在平面直角坐标系中,将△ABC向右平移4个单位长度得到△A1B1C1,再将△A1B1C1向上平移3个单位长度得到△A2B2C2,若将△A2B2C2看成是由△ABC经过一次平移得到的,则平移的距离是 个单位长度.
8.如△ABC和△AB'C'成中心对称,点A为对称中心,若∠C=90°,∠B=30°,BC=,则BB'的长为 .
9.如将等边三角形ABC沿BC方向平移得到△A1B1C1,A1B1与AC交于点P.若BC=3,=,则BB1= .
10.如△ABC是边长为4 cm的等边三角形,点D在AB边上(不与点A,B重合),将△ACD绕点C按逆时针方向旋转60°得到△BCE,连接DE,则△BDE周长的最小值是 cm.
三、解答题(共40分)
11.(13分)如,在平面直角坐标系中,有一Rt△ABC,且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
(1)旋转中心的坐标是 ,旋转角的度数是 ;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°,180°得到的三角形;
(3)利用变换前后所形成的如图案,可以证明的定理是 .
12.(13分)如,在△ABC中,AD平分∠BAC交BC于点D.
(1)如如图①,将△ABD沿BC方向平移,使点D移至点C的位置,得到△A'B'D',且A'B'交AC于点E,猜想∠B'EC与∠A'之间的数量关系,并说明理由;(2)如如图②,将△ABD沿AC方向平移,使AB的对应边A'B'经过点D,得到△A'B'D'.求证:A'D'平分∠B'A'C.
13.(14分)如①所示,△ABC,△ECD都是等边三角形,点E在BC上.
(1)试确定AE,BD之间的大小关系;
(2)如果把△ECD绕点C按逆时针方向旋转到如如图②所示的位置,那么(1)中的结论还成立吗 请说明理由.
答案
自我综合评价(三)
1.D 2.B
3.C 解: 因为点A与点O对应,点A(-1,0),点O(0,0),所以如图形向右平移1个单位长度,所以点B的对应点B'的坐标为(0+1,),即(1,).
4.C 解: (10-1)×7=9×7=63(m2).
故这块草地的绿地面积为63 m2.
故选C.
5.C 解: ∵将△ABC绕点C顺时针旋转90°得到△EDC,
∴∠DCE=∠ACB=20°,∠ACE=90°,AC=CE,∴∠ACD=90°-20°=70°.
∵点A,D,E在同一条直线上,∠ACE=90°,AC=CE,∴∠DAC=45°.
在△ADC中,∠ADC+∠DAC+∠ACD=180°,即∠ADC+45°+70°=180°,解得∠ADC=65°.
6.A
7.5 解: 平移的距离是=5(个)单位长度.
8.4
9.1 解: 过点P作PD⊥B1C于点D.
∵将等边三角形ABC沿BC方向平移得到△A1B1C1,∴∠PB1C=∠B=∠ACB=60°,
∴∠CPB1=60°,∴△PCB1是等边三角形.
设等边三角形PCB1的边长是2a,则B1D=CD=a,由勾股定理得PD=a.
∵=,∴·2a·a=,解得a=1(负值已舍去),
∴B1C=2,∴BB1=3-2=1.故答案为1.
10.(4+2) 解: ∵将△ACD绕点C按逆时针方向旋转60°得到△BCE,∴AD=BE,∠DCE=60°,CD=CE,∴△CDE是等边三角形,∴CD=DE,∴△BDE的周长=BD+BE+DE=BD+AD+CD=AB+CD=4+CD,∴当CD取最小值时,△BDE的周长有最小值.∵当CD⊥AB时,CD有最小值为2,∴△BDE周长的最小值为(4+2)cm.
11.解:(1)(0,0) 90°
(2)如如图,△A1AC1顺时针旋转90°,180°得到的三角形分别是△A2A1C2,△BA2C3.
(3)勾股定理
12.解:(1)∠B'EC=2∠A'.理由如下:∵△A'B'D'是由△ABD平移所得,
∴A'B'∥AB,∠A'=∠BAD,∴∠B'EC=∠BAC.∵AD平分∠BAC,∴∠BAC=2∠BAD,
∴∠B'EC=2∠A'.
(2)证明:∵△A'B'D'是由△ABD平移所得,∴A'B'∥AB,∠B'A'D'=∠BAD,
∴∠B'A'C=∠BAC.∵AD平分∠BAC,∴∠BAC=2∠BAD,
∴∠B'A'C=2∠B'A'D',∴A'D'平分∠B'A'C.
13.解:(1)∵△ABC和△ECD都是等边三角形,∴AC=BC,∠ACB=∠ECD=60°,CE=CD,
∴△ACE≌△BCD,∴AE=BD.
(2)成立.理由如下:由(1)知AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACE=∠BCD.在△ACE和△BCD中,
∵AC=BC,∠ACE=∠BCD,CE=CD,
∴△ACE≌△BCD,
∴AE=BD.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
