北师大版数学八年级下册同步课时练习:第三章 如图形的平移与旋转 单元复习小结 (word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册同步课时练习:第三章 如图形的平移与旋转 单元复习小结 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 300.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 09:29:05 | ||
图片预览

文档简介
单元复习小结
类型之一 如图形的平移
1.在平面直角坐标系xOy中,A(2,4),B(-2,3),C(4,-1),将线段AB平移得到线段CD,其中点A的对应点是C,则点B的对应点D的坐标为( )
A.(-4,8) B.(4,-8) C.(0,2) D.(0,-2)
2.如将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD,CE,若△ACD的面积为10,则△BCE的面积为( )
A.5 B.6 C.10 D.4
3.如在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1(点A与点A1,点B与点B1,点C与点C1分别对应),点P的对应点为P1(a+6,b-2).
(1)写出△A1B1C1各点的坐标:A1( , ),B1( , ),C1( , );
(2)在如图中画出△A1B1C1;
(3)求△A1B1C1的面积;
(4)在x轴上找一点M,使得△MB1C1的周长最短.直接写出点M的坐标.
类型之二 如图形的旋转
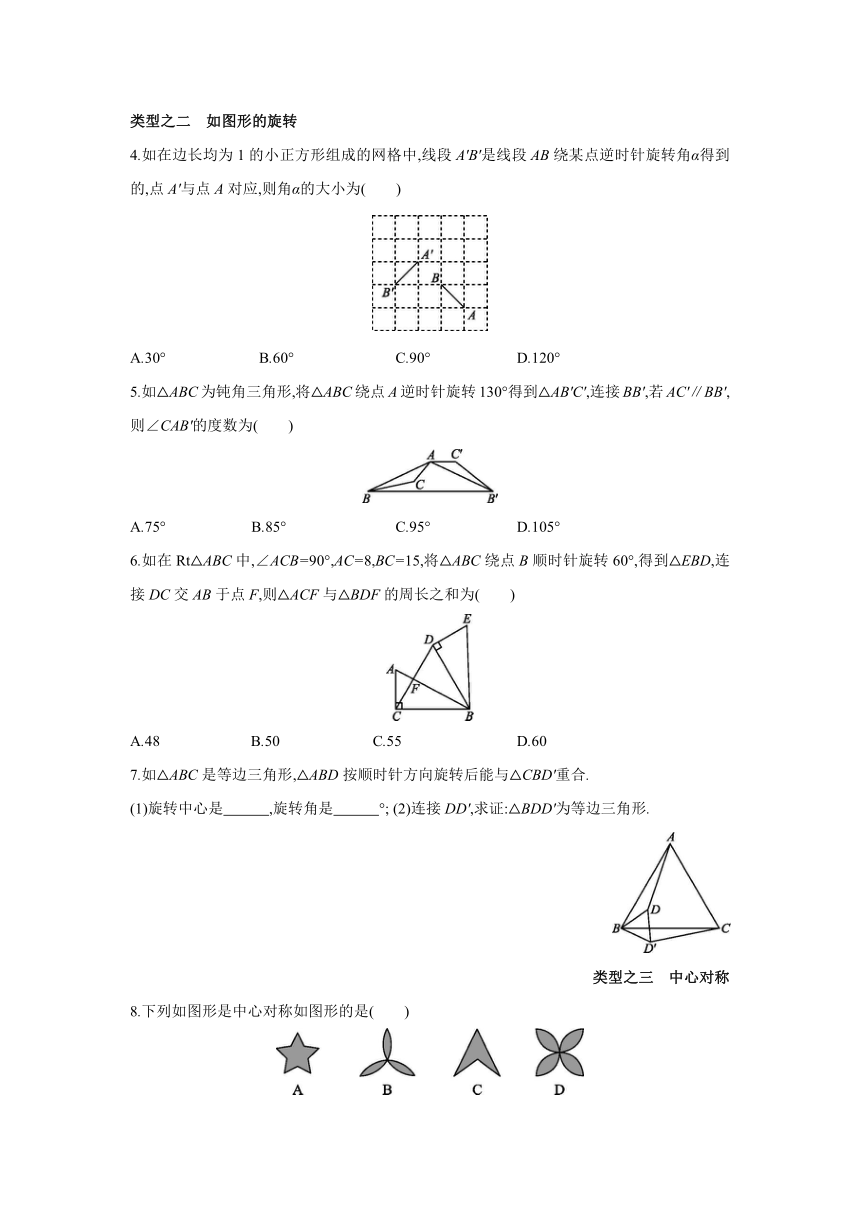
4.如在边长均为1的小正方形组成的网格中,线段A'B'是线段AB绕某点逆时针旋转角α得到的,点A'与点A对应,则角α的大小为( )
A.30° B.60° C.90° D.120°
5.如△ABC为钝角三角形,将△ABC绕点A逆时针旋转130°得到△AB'C',连接BB',若AC'∥BB',则∠CAB'的度数为( )
A.75° B.85° C.95° D.105°
6.如在Rt△ABC中,∠ACB=90°,AC=8,BC=15,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC交AB于点F,则△ACF与△BDF的周长之和为( )
A.48 B.50 C.55 D.60
7.如△ABC是等边三角形,△ABD按顺时针方向旋转后能与△CBD'重合.
(1)旋转中心是 ,旋转角是 °; (2)连接DD',求证:△BDD'为等边三角形.
类型之三 中心对称
8.下列如图形是中心对称如图形的是( )
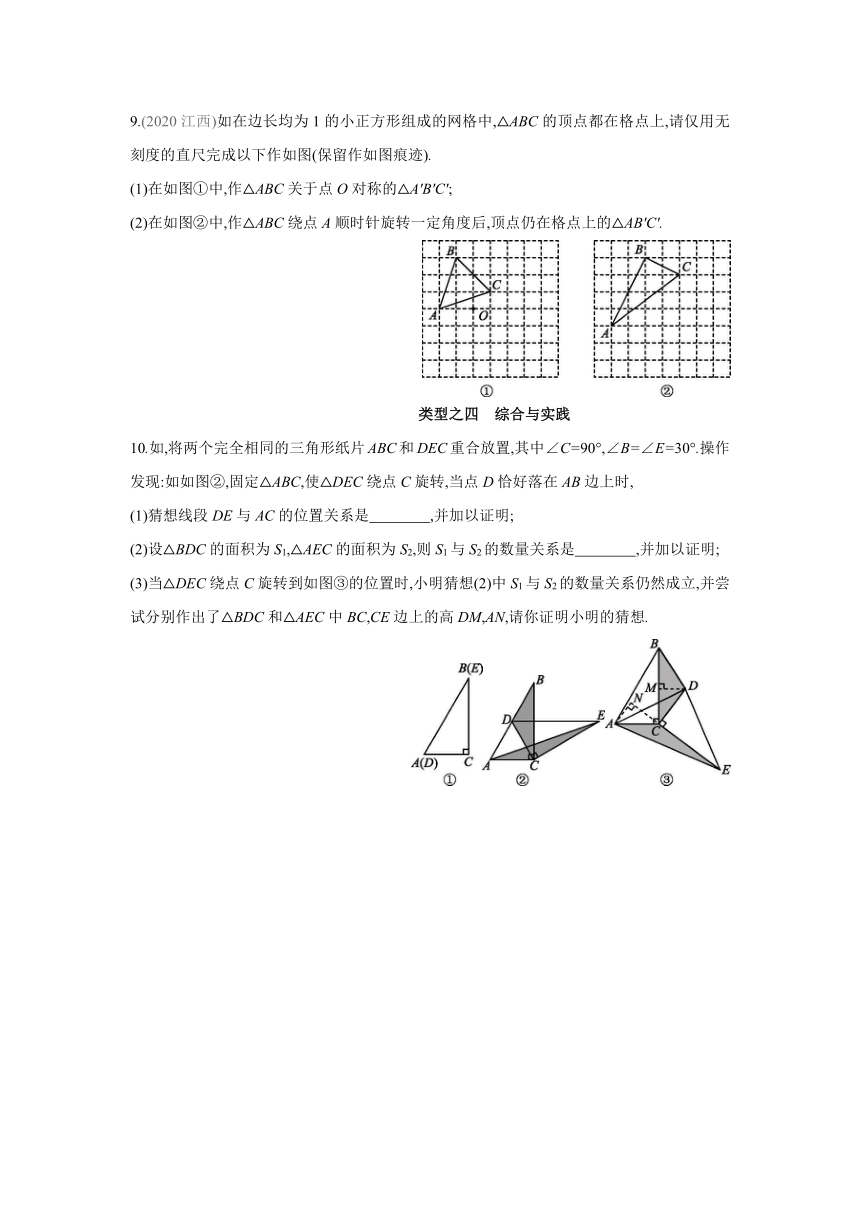
9.(2020江西)如在边长均为1的小正方形组成的网格中,△ABC的顶点都在格点上,请仅用无刻度的直尺完成以下作如图(保留作如图痕迹).
(1)在如图①中,作△ABC关于点O对称的△A'B'C';
(2)在如图②中,作△ABC绕点A顺时针旋转一定角度后,顶点仍在格点上的△AB'C'.
类型之四 综合与实践
10.如,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.操作发现:如如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,
(1)猜想线段DE与AC的位置关系是 ,并加以证明;
(2)设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 ,并加以证明;
(3)当△DEC绕点C旋转到如图③的位置时,小明猜想(2)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高DM,AN,请你证明小明的猜想.
答案
回顾与思考
1.D 解: ∵点A(2,4)的对应点C的坐标为(4,-1),∴平移规律为向右平移2个单位长度,向下平移5个单位长度,
∴点B(-2,3)的对应点D的坐标为(0,-2).
2.A 解: ∵△ABC沿直线AB向右平移后到达△BDE的位置,
∴AB=BD,BC∥DE,
∴S△ABC=S△BCD=S△ACD=×10=5.∵BC∥DE,
∴S△BCE=S△BCD=5.
3.解:(1)3 1 1 -1 4 -2
(2)如如图所示,△A1B1C1即为所求.
(3)△A1B1C1的面积为3×3-×2×2-×1×3-×1×3=4.
(4)如如图,作点B1关于x轴的对称点B1',连接B1'C1交x轴于点M,则点M即为所求.点M的坐标为(2,0).
4.C 解: 如如图,连接AA',BB',作线段AA',BB'的垂直平分线交点为O,点O即为旋转中心.连接OA.
∠AOA'即为旋转角,
∴旋转角为90°.
故选C.
5.D 解: ∵将△ABC绕点A按逆时针方向旋转130°得到△AB'C',
∴∠BAB'=∠CAC'=130°,AB=AB',∴∠AB'B=×(180°-130°)=25°.
∵AC'∥BB',∴∠C'AB'=∠AB'B=25°,∴∠CAB'=∠CAC'-∠C'AB'=130°-25°=105°.
6.C 解: ∵将△ABC绕点B顺时针旋转60°,得到△EBD,∴△ABC≌△EBD,∠CBD=60°,∴BD=BC=15,∴△BCD为等边三角形,∴CD=BC=BD=15.∵AB===17,
∴△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=8+17+15+15=
55.
7.解:(1)点B 60
(2)证明:由旋转的性质,得BD=BD'.
∵旋转角是60°,
∴∠DBD'=60°,
∴△BDD'为等边三角形.
8.D
9.解:(1)分别作出点A,B,C的对应点A',B',C',连接A'B',B'C',C'A',如如图①,△A'B'C'即为所求.
(2)如如图②,△AB'C'即为所求.
10.解:(1)DE∥AC
证明:∵△DEC绕点C旋转,点D恰好落在AB边上,
∴AC=CD.
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠BAC=90°-30°=60°,
∴△ACD是等边三角形,∴∠ACD=60°.
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,∴DE∥AC.
(2)S1=S2
证明:由(1)知△ACD是等边三角形,
∴AC=CD=AD.
∵∠B=30°,∠ACB=90°,
∴CD=AC=AD=AB,
∴BD=AD=AC.
根据等边三角形的性质,△ACD的边AC,AD上的高相等,又DE∥AC,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2.
(3)证明:由题意,得BC=CE,AC=CD.
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,∴∠ACN=∠DCM.
在△ACN和△DCM中,
∵∠ACN=∠DCM,∠N=∠CMD=90°,
AC=DC,∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2.
类型之一 如图形的平移
1.在平面直角坐标系xOy中,A(2,4),B(-2,3),C(4,-1),将线段AB平移得到线段CD,其中点A的对应点是C,则点B的对应点D的坐标为( )
A.(-4,8) B.(4,-8) C.(0,2) D.(0,-2)
2.如将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD,CE,若△ACD的面积为10,则△BCE的面积为( )
A.5 B.6 C.10 D.4
3.如在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1(点A与点A1,点B与点B1,点C与点C1分别对应),点P的对应点为P1(a+6,b-2).
(1)写出△A1B1C1各点的坐标:A1( , ),B1( , ),C1( , );
(2)在如图中画出△A1B1C1;
(3)求△A1B1C1的面积;
(4)在x轴上找一点M,使得△MB1C1的周长最短.直接写出点M的坐标.
类型之二 如图形的旋转
4.如在边长均为1的小正方形组成的网格中,线段A'B'是线段AB绕某点逆时针旋转角α得到的,点A'与点A对应,则角α的大小为( )
A.30° B.60° C.90° D.120°
5.如△ABC为钝角三角形,将△ABC绕点A逆时针旋转130°得到△AB'C',连接BB',若AC'∥BB',则∠CAB'的度数为( )
A.75° B.85° C.95° D.105°
6.如在Rt△ABC中,∠ACB=90°,AC=8,BC=15,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC交AB于点F,则△ACF与△BDF的周长之和为( )
A.48 B.50 C.55 D.60
7.如△ABC是等边三角形,△ABD按顺时针方向旋转后能与△CBD'重合.
(1)旋转中心是 ,旋转角是 °; (2)连接DD',求证:△BDD'为等边三角形.
类型之三 中心对称
8.下列如图形是中心对称如图形的是( )
9.(2020江西)如在边长均为1的小正方形组成的网格中,△ABC的顶点都在格点上,请仅用无刻度的直尺完成以下作如图(保留作如图痕迹).
(1)在如图①中,作△ABC关于点O对称的△A'B'C';
(2)在如图②中,作△ABC绕点A顺时针旋转一定角度后,顶点仍在格点上的△AB'C'.
类型之四 综合与实践
10.如,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.操作发现:如如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,
(1)猜想线段DE与AC的位置关系是 ,并加以证明;
(2)设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 ,并加以证明;
(3)当△DEC绕点C旋转到如图③的位置时,小明猜想(2)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高DM,AN,请你证明小明的猜想.
答案
回顾与思考
1.D 解: ∵点A(2,4)的对应点C的坐标为(4,-1),∴平移规律为向右平移2个单位长度,向下平移5个单位长度,
∴点B(-2,3)的对应点D的坐标为(0,-2).
2.A 解: ∵△ABC沿直线AB向右平移后到达△BDE的位置,
∴AB=BD,BC∥DE,
∴S△ABC=S△BCD=S△ACD=×10=5.∵BC∥DE,
∴S△BCE=S△BCD=5.
3.解:(1)3 1 1 -1 4 -2
(2)如如图所示,△A1B1C1即为所求.
(3)△A1B1C1的面积为3×3-×2×2-×1×3-×1×3=4.
(4)如如图,作点B1关于x轴的对称点B1',连接B1'C1交x轴于点M,则点M即为所求.点M的坐标为(2,0).
4.C 解: 如如图,连接AA',BB',作线段AA',BB'的垂直平分线交点为O,点O即为旋转中心.连接OA.
∠AOA'即为旋转角,
∴旋转角为90°.
故选C.
5.D 解: ∵将△ABC绕点A按逆时针方向旋转130°得到△AB'C',
∴∠BAB'=∠CAC'=130°,AB=AB',∴∠AB'B=×(180°-130°)=25°.
∵AC'∥BB',∴∠C'AB'=∠AB'B=25°,∴∠CAB'=∠CAC'-∠C'AB'=130°-25°=105°.
6.C 解: ∵将△ABC绕点B顺时针旋转60°,得到△EBD,∴△ABC≌△EBD,∠CBD=60°,∴BD=BC=15,∴△BCD为等边三角形,∴CD=BC=BD=15.∵AB===17,
∴△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=8+17+15+15=
55.
7.解:(1)点B 60
(2)证明:由旋转的性质,得BD=BD'.
∵旋转角是60°,
∴∠DBD'=60°,
∴△BDD'为等边三角形.
8.D
9.解:(1)分别作出点A,B,C的对应点A',B',C',连接A'B',B'C',C'A',如如图①,△A'B'C'即为所求.
(2)如如图②,△AB'C'即为所求.
10.解:(1)DE∥AC
证明:∵△DEC绕点C旋转,点D恰好落在AB边上,
∴AC=CD.
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠BAC=90°-30°=60°,
∴△ACD是等边三角形,∴∠ACD=60°.
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,∴DE∥AC.
(2)S1=S2
证明:由(1)知△ACD是等边三角形,
∴AC=CD=AD.
∵∠B=30°,∠ACB=90°,
∴CD=AC=AD=AB,
∴BD=AD=AC.
根据等边三角形的性质,△ACD的边AC,AD上的高相等,又DE∥AC,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2.
(3)证明:由题意,得BC=CE,AC=CD.
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,∴∠ACN=∠DCM.
在△ACN和△DCM中,
∵∠ACN=∠DCM,∠N=∠CMD=90°,
AC=DC,∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
