北师大版数学八年级下册同步课时练习:第一章 三角形的证明 单元复习小结 (word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册同步课时练习:第一章 三角形的证明 单元复习小结 (word版含答案) | 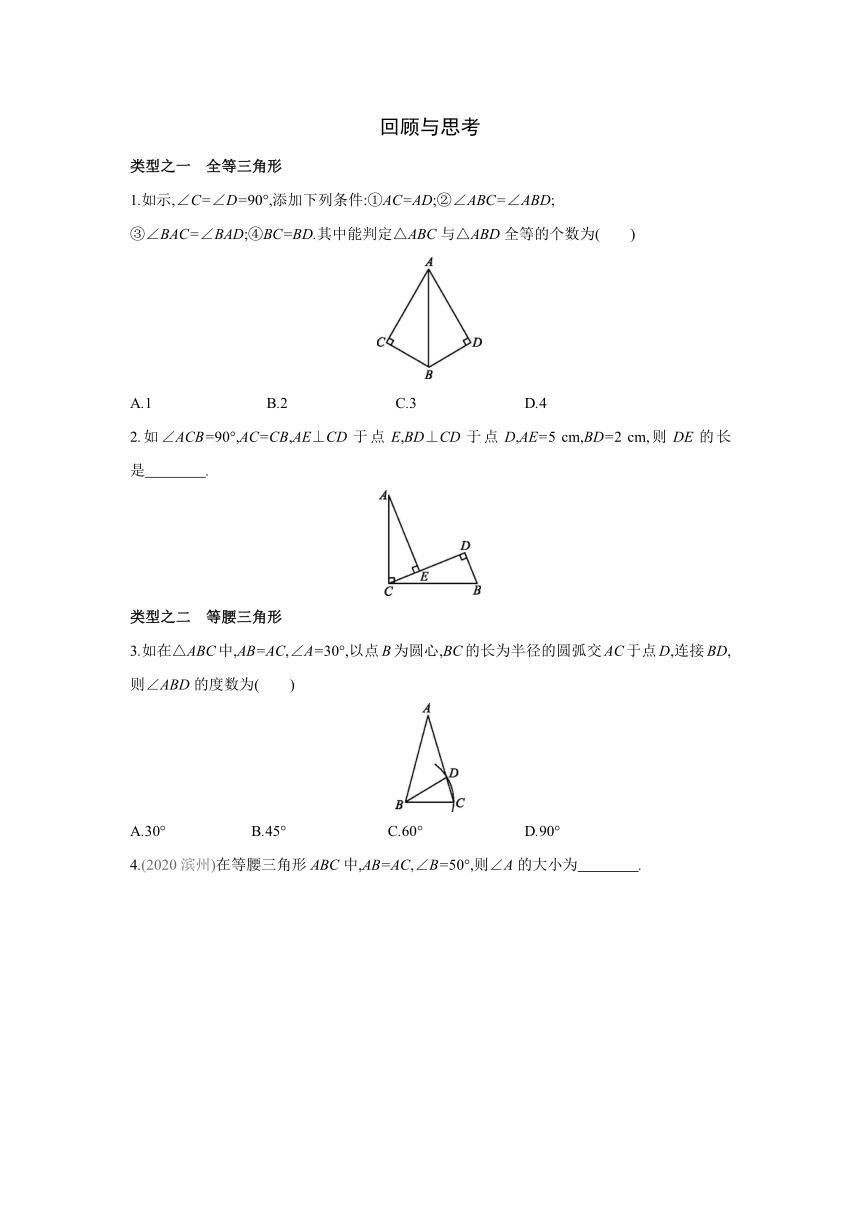 | |
| 格式 | docx | ||
| 文件大小 | 259.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 09:30:13 | ||
图片预览




文档简介
回顾与思考
类型之一 全等三角形
1.如示,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;
③∠BAC=∠BAD;④BC=BD.其中能判定△ABC与△ABD全等的个数为( )
A.1 B.2 C.3 D.4
2.如∠ACB=90°,AC=CB,AE⊥CD于点E,BD⊥CD于点D,AE=5 cm,BD=2 cm,则DE的长是 .
类型之二 等腰三角形
3.如在△ABC中,AB=AC,∠A=30°,以点B为圆心,BC的长为半径的圆弧交AC于点D,连接BD,则∠ABD的度数为( )
A.30° B.45° C.60° D.90°
4.(2020滨州)在等腰三角形ABC中,AB=AC,∠B=50°,则∠A的大小为 .
5.如在△ABC中,BA=BC,BD平分∠ABC,则∠2-∠1= °.
6.如点E在△ABC的AC边的延长线上,点D在AB边上,DE交BC于点F,DF=EF,
BD=CE.求证:△ABC是等腰三角形.
类型之三 直角三角形
7.如已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM的长为( )
A.3 B.4 C.5 D.6
8.已知一个直角三角形的周长是20+4,斜边的长为4,则这个三角形的面积是( )
A.96 B.48 C.24 D.192
9.(2020绥化)在Rt△ABC中,∠C=90°,若AB-AC=2,BC=8,则AB的长是 .
10.如点D,A,E在直线l上,AB=CA,BD⊥l于点D,CE⊥l于点E,且BD=AE.若BD=3,CE=4,求BC的长.
类型之四 角平分线和线段的垂直平分线
11.如点I到△ABC三边的距离相等,AB=6,AC=4,BC=3,将∠ACB平移使其顶点与点I重合,则如图中阴影部分的周长为( )
A.6 B.4 C.3 D.6.5
12.如示,已知∠O及边上两点A和B,用直尺和圆规在∠O的平分线上求作点P,使得△ABP是以AB为底边的等腰三角形.(不写作法,保留作如图痕迹)
13.如,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
(1)试说明BE=CF;
(2)如果AB=5,AC=3,求AE,BE的长.
类型之五 综合与实践
14.如(a),已知点B(0,6),C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.(1)求证:BO=ED.
(2)如如图(b),当点D恰好落在BC上时,
①求OC的长及点E的坐标.
②在x轴上是否存在点P,使△PEC为等腰三角形 若存在,请写出点P的坐标;若不存在,请说明理由.
③如如图(c),M是线段BC上的动点(不与点B,C重合),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否会发生变化 若不发生变化,请直接写出MH+MG的值;若发生变化,请简要说明理由.
答案
回顾与思考
1.D 解: 当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得
Rt△ABC≌Rt△ABD(HL);②当∠ABC=∠ABD时,由∠C=∠D=90°,
∠ABC=∠ABD且AB=AB,可得△ABC≌△ABD(AAS);
③当∠BAC=∠BAD时,由∠C=∠D=90°,∠BAC=∠BAD且AB=AB,
可得△ABC≌△ABD(AAS);
④当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL).故选D.
2.3 cm 解: ∵AE⊥CD于点E,BD⊥CD于点D,
∴∠AEC=∠D=90°=∠ACB,
∴∠A+∠ACE=90°,∠ACE+∠BCD=90°,
∴∠A=∠BCD.
又∵AC=CB,
∴△ACE≌△CBD,
∴AE=CD=5 cm,CE=BD=2 cm,
∴DE=CD-CE=5-2=3(cm).
3.B 解: ∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=(180°-∠A)=×(180°-30°)=75°.
∵以点B为圆心,BC的长为半径的圆弧交AC于点D,∴BC=BD,
∴∠CBD=180°-2∠ACB=180°-2×75°=30°,∴∠ABD=∠ABC-∠CBD=75°-30°=45°.
故选B.
4.80° 解: ∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠A=180°-2×50°=80°.
5.90 解: 如如图,延长BD交AC于点E.
∵BA=BC,BD平分∠ABC,
∴BE⊥AC,
∴∠AEB=90°,
∴∠2-∠1=90°.
故答案为90.
6.证明:过点D作DG∥AC交BC于点G,如如图所示,
则∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,
∵∠GDF=∠E,DF=EF,∠DFG=∠EFC,
∴△GDF≌△CEF(ASA),
∴GD=CE.
∵BD=CE,∴BD=GD,
∴∠B=∠DGB,
则∠B=∠ACB,∴AB=AC,
∴△ABC是等腰三角形.
7.B 解: 如如图,过点P作PH⊥MN于点H.
∵PM=PN,MN=2,
∴MH=NH=MN=1.
∵∠AOB=60°,
∴∠OPH=30°,
∴OH=OP=5,
∴OM=OH-MH=4.故选B.
8.B 解: ∵直角三角形的周长是20+4,斜边的长为4,
∴两直角边长和为20,设其中一条直角边长为x,则另一边长为(20-x),
∴x2+(20-x)2=(4)2,
解得x1=8,x2=12,
∴两直角边长分别为8,12,
∴S=×8×12=48.
故选B.
9.17 解: ∵在Rt△ABC中,∠C=90°,AB-AC=2,BC=8,
∴AC2+BC2=AB2,
即(AB-2)2+82=AB2,
解得AB=17.
10.解:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°.
在Rt△ABD和Rt△CAE中,
∵AB=CA,BD=AE,
∴Rt△ABD≌Rt△CAE(HL),
∴AD=CE=4,AE=BD=3,∠DAB=∠ECA,
∴AC=AB===5.
∵∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°,
∴∠BAC=180°-(∠BAD+∠CAE)=90°,
∴BC===5.
11.A 解: 如如图,连接AI,BI.
∵点I到△ABC三边的距离相等,
∴AI平分∠BAC,BI平分∠ABC,
∴∠CAI=∠DAI,∠CBI=∠EBI.
∵∠ACB平移使其顶点与点I重合,
∴DI∥AC,EI∥BC,
∴∠CAI=∠DIA,∠CBI=∠EIB,
∴∠DIA=∠DAI,∠EIB=∠EBI,
∴DI=DA,EI=EB,
∴DI+DE+EI=DA+DE+EB=AB=6,
即如图中阴影部分的周长为6.
故选A.
12.解: 作∠AOB的平分线和AB的垂直平分线,它们的交点即为所求作的点P.
解:如如图,点P即为所作.
13.解:(1)如如图,连接BD,CD.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°.
∵DG⊥BC且平分BC,
∴BD=CD.
在Rt△BED与Rt△CFD中,
∵BD=CD,DE=DF,
∴Rt△BED≌Rt△CFD(HL),∴BE=CF.
(2)在△AED和△AFD中,∵∠AED=∠AFD=90°,∠EAD=∠FAD,AD=AD,
∴△AED≌△AFD(AAS),∴AE=AF.
设BE=x,则CF=x.∵AB=5,AC=3,AE=AB-BE,AF=AC+CF,∴5-x=3+x,解得x=1,∴BE=1,
∴AE=AB-BE=5-1=4.
14.解:(1)证明:∵△ODC和△EBC都是等边三角形,
∴OC=DC,BC=EC,∠OCD=∠BCE=60°,
∴∠BCO=∠ECD,
∴△OBC≌△DEC(SAS),∴BO=ED.
(2)①OC=2,点E的坐标为(4,6).
②存在,点P的坐标为(-2,0)或(6,0).
③MH+MG的值不会发生变化,MH+MG=6.
类型之一 全等三角形
1.如示,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;
③∠BAC=∠BAD;④BC=BD.其中能判定△ABC与△ABD全等的个数为( )
A.1 B.2 C.3 D.4
2.如∠ACB=90°,AC=CB,AE⊥CD于点E,BD⊥CD于点D,AE=5 cm,BD=2 cm,则DE的长是 .
类型之二 等腰三角形
3.如在△ABC中,AB=AC,∠A=30°,以点B为圆心,BC的长为半径的圆弧交AC于点D,连接BD,则∠ABD的度数为( )
A.30° B.45° C.60° D.90°
4.(2020滨州)在等腰三角形ABC中,AB=AC,∠B=50°,则∠A的大小为 .
5.如在△ABC中,BA=BC,BD平分∠ABC,则∠2-∠1= °.
6.如点E在△ABC的AC边的延长线上,点D在AB边上,DE交BC于点F,DF=EF,
BD=CE.求证:△ABC是等腰三角形.
类型之三 直角三角形
7.如已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM的长为( )
A.3 B.4 C.5 D.6
8.已知一个直角三角形的周长是20+4,斜边的长为4,则这个三角形的面积是( )
A.96 B.48 C.24 D.192
9.(2020绥化)在Rt△ABC中,∠C=90°,若AB-AC=2,BC=8,则AB的长是 .
10.如点D,A,E在直线l上,AB=CA,BD⊥l于点D,CE⊥l于点E,且BD=AE.若BD=3,CE=4,求BC的长.
类型之四 角平分线和线段的垂直平分线
11.如点I到△ABC三边的距离相等,AB=6,AC=4,BC=3,将∠ACB平移使其顶点与点I重合,则如图中阴影部分的周长为( )
A.6 B.4 C.3 D.6.5
12.如示,已知∠O及边上两点A和B,用直尺和圆规在∠O的平分线上求作点P,使得△ABP是以AB为底边的等腰三角形.(不写作法,保留作如图痕迹)
13.如,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
(1)试说明BE=CF;
(2)如果AB=5,AC=3,求AE,BE的长.
类型之五 综合与实践
14.如(a),已知点B(0,6),C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.(1)求证:BO=ED.
(2)如如图(b),当点D恰好落在BC上时,
①求OC的长及点E的坐标.
②在x轴上是否存在点P,使△PEC为等腰三角形 若存在,请写出点P的坐标;若不存在,请说明理由.
③如如图(c),M是线段BC上的动点(不与点B,C重合),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否会发生变化 若不发生变化,请直接写出MH+MG的值;若发生变化,请简要说明理由.
答案
回顾与思考
1.D 解: 当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得
Rt△ABC≌Rt△ABD(HL);②当∠ABC=∠ABD时,由∠C=∠D=90°,
∠ABC=∠ABD且AB=AB,可得△ABC≌△ABD(AAS);
③当∠BAC=∠BAD时,由∠C=∠D=90°,∠BAC=∠BAD且AB=AB,
可得△ABC≌△ABD(AAS);
④当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL).故选D.
2.3 cm 解: ∵AE⊥CD于点E,BD⊥CD于点D,
∴∠AEC=∠D=90°=∠ACB,
∴∠A+∠ACE=90°,∠ACE+∠BCD=90°,
∴∠A=∠BCD.
又∵AC=CB,
∴△ACE≌△CBD,
∴AE=CD=5 cm,CE=BD=2 cm,
∴DE=CD-CE=5-2=3(cm).
3.B 解: ∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=(180°-∠A)=×(180°-30°)=75°.
∵以点B为圆心,BC的长为半径的圆弧交AC于点D,∴BC=BD,
∴∠CBD=180°-2∠ACB=180°-2×75°=30°,∴∠ABD=∠ABC-∠CBD=75°-30°=45°.
故选B.
4.80° 解: ∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠A=180°-2×50°=80°.
5.90 解: 如如图,延长BD交AC于点E.
∵BA=BC,BD平分∠ABC,
∴BE⊥AC,
∴∠AEB=90°,
∴∠2-∠1=90°.
故答案为90.
6.证明:过点D作DG∥AC交BC于点G,如如图所示,
则∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,
∵∠GDF=∠E,DF=EF,∠DFG=∠EFC,
∴△GDF≌△CEF(ASA),
∴GD=CE.
∵BD=CE,∴BD=GD,
∴∠B=∠DGB,
则∠B=∠ACB,∴AB=AC,
∴△ABC是等腰三角形.
7.B 解: 如如图,过点P作PH⊥MN于点H.
∵PM=PN,MN=2,
∴MH=NH=MN=1.
∵∠AOB=60°,
∴∠OPH=30°,
∴OH=OP=5,
∴OM=OH-MH=4.故选B.
8.B 解: ∵直角三角形的周长是20+4,斜边的长为4,
∴两直角边长和为20,设其中一条直角边长为x,则另一边长为(20-x),
∴x2+(20-x)2=(4)2,
解得x1=8,x2=12,
∴两直角边长分别为8,12,
∴S=×8×12=48.
故选B.
9.17 解: ∵在Rt△ABC中,∠C=90°,AB-AC=2,BC=8,
∴AC2+BC2=AB2,
即(AB-2)2+82=AB2,
解得AB=17.
10.解:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°.
在Rt△ABD和Rt△CAE中,
∵AB=CA,BD=AE,
∴Rt△ABD≌Rt△CAE(HL),
∴AD=CE=4,AE=BD=3,∠DAB=∠ECA,
∴AC=AB===5.
∵∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°,
∴∠BAC=180°-(∠BAD+∠CAE)=90°,
∴BC===5.
11.A 解: 如如图,连接AI,BI.
∵点I到△ABC三边的距离相等,
∴AI平分∠BAC,BI平分∠ABC,
∴∠CAI=∠DAI,∠CBI=∠EBI.
∵∠ACB平移使其顶点与点I重合,
∴DI∥AC,EI∥BC,
∴∠CAI=∠DIA,∠CBI=∠EIB,
∴∠DIA=∠DAI,∠EIB=∠EBI,
∴DI=DA,EI=EB,
∴DI+DE+EI=DA+DE+EB=AB=6,
即如图中阴影部分的周长为6.
故选A.
12.解: 作∠AOB的平分线和AB的垂直平分线,它们的交点即为所求作的点P.
解:如如图,点P即为所作.
13.解:(1)如如图,连接BD,CD.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°.
∵DG⊥BC且平分BC,
∴BD=CD.
在Rt△BED与Rt△CFD中,
∵BD=CD,DE=DF,
∴Rt△BED≌Rt△CFD(HL),∴BE=CF.
(2)在△AED和△AFD中,∵∠AED=∠AFD=90°,∠EAD=∠FAD,AD=AD,
∴△AED≌△AFD(AAS),∴AE=AF.
设BE=x,则CF=x.∵AB=5,AC=3,AE=AB-BE,AF=AC+CF,∴5-x=3+x,解得x=1,∴BE=1,
∴AE=AB-BE=5-1=4.
14.解:(1)证明:∵△ODC和△EBC都是等边三角形,
∴OC=DC,BC=EC,∠OCD=∠BCE=60°,
∴∠BCO=∠ECD,
∴△OBC≌△DEC(SAS),∴BO=ED.
(2)①OC=2,点E的坐标为(4,6).
②存在,点P的坐标为(-2,0)或(6,0).
③MH+MG的值不会发生变化,MH+MG=6.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
