选择性必修第一册1.4空间向量的应用 同步练习(Word版含解析)
文档属性
| 名称 | 选择性必修第一册1.4空间向量的应用 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 17:29:05 | ||
图片预览




文档简介
人教A版(2019)选择性必修第一册 1.4 空间向量的应用 同步练习
一、单选题
1.在空间直角坐标系内,平面经过三点,向量是平面的一个法向量,则( )
A. B. C.5 D.7
2.如图,在底面为正方形的四棱锥P-ABCD中,已知PA⊥平面ABCD,且PA=.若点M为PD中点,则直线CM与PB所成角的大小为( )
A.60° B.45° C.30° D.90°
3.如图,在三棱锥中,为等边三角形,为等腰直角三角形,,平面平面,为的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
4.已知正四棱锥,侧棱长是底面边长的2倍,是的中点,则所成的角的余弦值为( )
A. B. C. D.
5.二面角--为60°,A、B是棱上的两点,、分别在半平面内,,,且,,则的长为( )
A. B. C. D.
6.已知四边形ABCD为正方形,P为平面ABCD外一点,PD⊥AD,PD=AD=2,二面角P-AD-C为60°,则P到AB的距离是( )
A.2 B.
C.2 D.
7.若O为坐标原点, =(1,1,-2),=(3,2,8),=(0,1,0),则线段AB的中点P到点C的距离为( )
A. B.
C. D.
8.已知,,则平面ABC的一个单位法向量为( )
A. B.
C. D.
9.如图,在三棱锥中,已知,,平面平面,则异面直线与所成角的余弦值为( )
A. B. C. D.
10.在棱长为的正方体中,是的中点,则点到平面的距离是( )
A. B. C. D.
11.直三棱柱ABC-A1B1C1中,△ABC为等边三角形, AA1=AB,M是A1C1的中点,则AM与平面所成角的正弦值为( )
A. B. C. D.
12.若平面α,β的法向量分别为,,则下列结论中正确的是( )
A. B.α,β相交但不垂直
C. D.或α,β重合
二、填空题
13.若向量是直线l的方向向量,向量是平面α的法向量,则直线l与平面α所成的角为______.
14.如图,四棱柱的底面是正方形,为底面中心,平面,.平面的法向量________.
15.如图所示,已知点P为菱形ABCD外一点,且平面ABCD,,点F为PC的中点,则二面角的正切值为__________
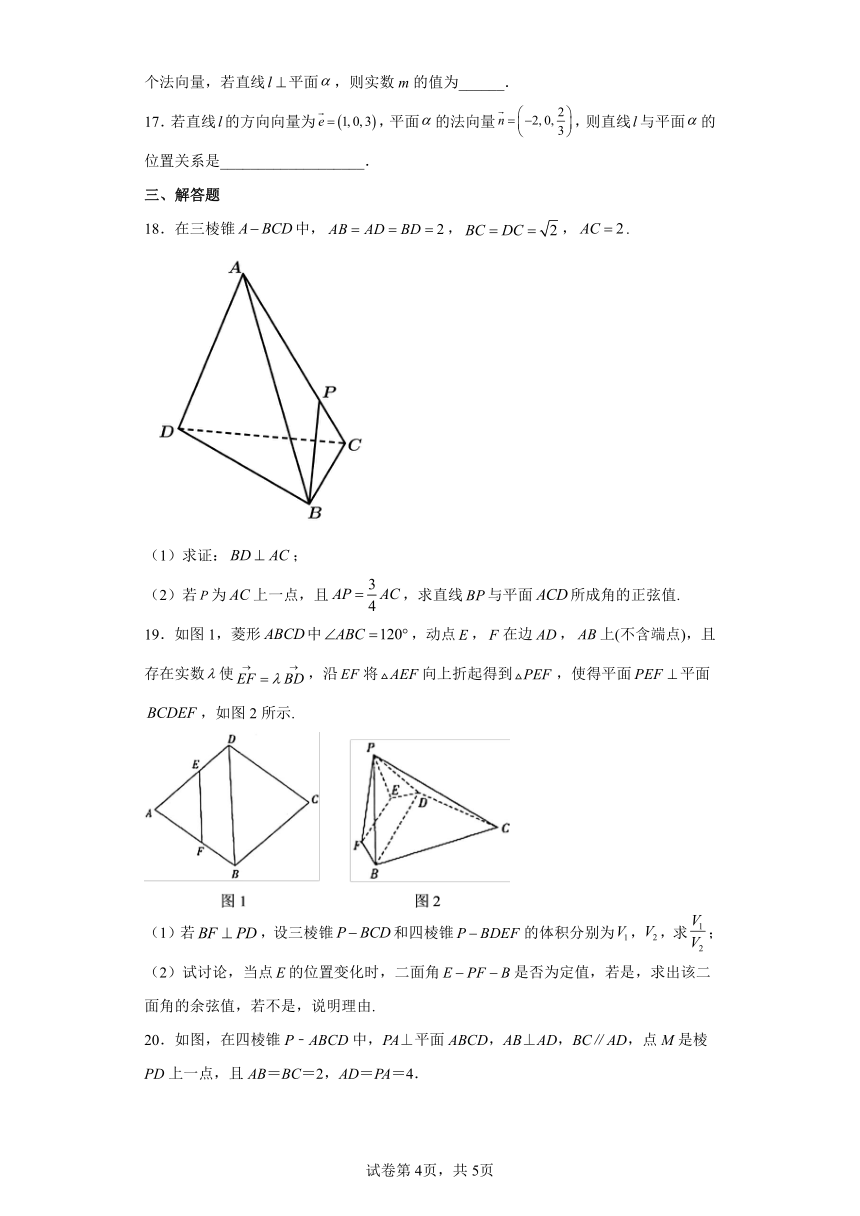
16.已知向量是直线l的一个方向向量,向量是平面的一个法向量,若直线平面,则实数m的值为______.
17.若直线的方向向量为,平面的法向量,则直线与平面的位置关系是___________________.
三、解答题
18.在三棱锥中,,,.
(1)求证:;
(2)若为上一点,且,求直线与平面所成角的正弦值.
19.如图1,菱形中,动点,在边,上(不含端点),且存在实数使,沿将向上折起得到,使得平面平面,如图2所示.
(1)若,设三棱锥和四棱锥的体积分别为,,求;
(2)试讨论,当点的位置变化时,二面角是否为定值,若是,求出该二面角的余弦值,若不是,说明理由.
20.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AB⊥AD,BC∥AD,点M是棱PD上一点,且AB=BC=2,AD=PA=4.
(1)若PM:MD=1:2,求证:PB∥平面ACM;
(2)求二面角A﹣CD﹣P的正弦值;
(3)若直线AM与平面PCD所成角的正弦值为,求MD的长.
21.如图,已知平面,底面为正方形,,分别为的中点.
(1)求证:平面;
(2)求与平面所成角的正弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
求出,,利用与数量积为0,求解即可.
【详解】
,
可得,,
故选:D
2.C
以为坐标原点建立空间直角坐标系,求出,,利用向量法即可求出.
【详解】
如图所示:以为坐标原点,以,,为单位向量建立空间直角坐标系,
设,则,,,,,
故,,
故,
由异面直线夹角的范围是,故直线与所成角的大小为.
故选:C.
3.B
取的中点,连接,根据等腰三角形的性质以及面面垂直的性质证明两两垂直,以为坐标原点,建立如图所示的空间直角坐标系,求出各点坐标以及和的坐标,由空间向量夹角公式计算即可求解.
【详解】
取的中点,连接,因为,所以
又因为平面平面,平面平面,面,
所以平面,
又因为,,可得两两垂直,
所以以为坐标原点,建立如图所示的空间直角坐标系,
因为是等腰直角三角形,,为等边三角形,
可得,,,,
所以,,
所以,
设异面直线与所成角为,则
所以异面直线与所成角的余弦值为,
故选:B.
4.C
建立空间直角坐标系,利用空间向量法求出异面直线所成角的余弦值.
【详解】
解:如图所示建立空间直角坐标系,
不妨设,则,,所以
,,, ,, .
.
与所成角的余弦值为.
故选:.
5.D
由已知条件和空间向量加法可得,再根据向量模和数量积的关系可得 ,由此能求出的长.
【详解】
因为二面角--为60°,A、B是棱上的两点,、分别在半平面内,,,
所以,,
又
所以
.
所以的长为.
故选:D.
本题考查空间线段长的求法,是中档题,解题时要认真审题,注意向量法的合理运用.
6.D
先作出P到AB的距离PE,再解三角形求出PE.
【详解】
因为ABCD为正方形,所以AD⊥DC.
由 ∠PDC为二面角P-AD-C的平面角,即∠PDC=60°.
如图所示,过P作PH⊥DC于H.
∵,∴AD⊥面PDC.,∴AD⊥面PH.
又PH⊥DC, ,∴PH⊥面ABCD,
在平面AC内过H作HE⊥AB于E,连接PE,则PE⊥AB,
所以线段PE即为所求.
以H为坐标原点建立空间直角坐标系,
则
所以,∴
故选:D.
方法点睛:
距离的计算方法有两类:
(1)几何法:利用几何图形求值;
(2)向量法:把距离用向量表示出来,转化为代数计算.
7.D
先求出的坐标,再利用三角形减法法则求的坐标,再求||即得解.
【详解】
由题意= (+)=,=-=,||=.
故答案为D
本题主要考查向量的坐标运算,考查向量的三角形法则和平行四边形法则,考查向量的模的计算,意在考查学生对这些知识的掌握水平和分析推理能力.
8.B
设平面的法向量为,进而得,再根据为单位向量即可得答案.
【详解】
设平面的法向量为,
则有取,则.
所以.因为,
所以平面的一个单位法向量可以是.
故选:B
本题考查平面的法向量的求法,考查运算求解能力,解题得关键在于掌握单位向量的表示形式,是中档题.
9.A
取的中点为,连接,证明平面,,然后建立空间直角坐标系,利用向量求解即可.
【详解】
取的中点为,连接
因为,所以,
因为平面平面,平面平面,平面
所以平面
因为,
所以
如图建立空间直角坐标系,则
所以
所以异面直线与所成角的余弦值为
故选:A
10.A
以为空间直角坐标原点建立空间直角坐标系,通过点面距离公式,计算点到平面的距离.
【详解】
以为空间直角坐标原点,分别为轴建立空间直角坐标系.由于是中点,故,且,设是平面的法向量,故,故可设,故到平面的距离.故选A.
本小题主要考查利用空间向量计算点到面的距离.计算过程中要先求得平面的法向量.属于基础题.
11.B
取的中点,以为原点,所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,即可根据线面角的向量公式求出.
【详解】
如图所示,取的中点,以为原点,所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
不妨设,则,
所以,平面的一个法向量为
设AM与平面所成角为,向量与所成的角为,
所以,
即AM与平面所成角的正弦值为.
故选:B.
12.D
根据题意,结合面面位置关系的向量证明,即可求解.
【详解】
根据题意,易知,故平面α,β的法向量共线,因此或α,β重合.
故选:D.
13.##
直接利用向量的夹角公式求解即可
【详解】
设直线l与平面α所成的角为,则由题意得
,
因为,
所以,
所以直线l与平面α所成的角为,
故答案为:
14.(答案不唯一)
易知,,从而可得,结合,,从而解得
【详解】
是正方形,且,
,
,
,,
,
,
,,
,
故,
故,
∵向量是平面OCB1的法向量,
,
,
故,,取,故,
平面的法向量
故答案为:(答案不唯一)
本题考查平面的法向量,建系求解即可,主要考查学生的运算能力,属于基础题.
15.
分析空间几何体的特征,建立合适的空间直角坐标系,用空间向量求二面角的余弦值,再求正切值﹒
【详解】
如图所示,连接BD,,连接OF,
以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴建立空间直角坐标系Oxyz.
设,则.
所以,,,.
结合图形可知,,且为平面BOF的法向量,
由,,
可求得平面BCF的一个法向量为.
所以,,
所以.
故答案为:
16.-2
由已知可得,即,计算即可得出结果.
【详解】
因为是直线的一个方向向量,是平面的一个法向量,且直线平面,所以,
所以,解得.
故答案为:-2.
17.或
由空间向量数量积的坐标表示可得,再由线面位置关系即可求解.
【详解】
因为直线的方向向量为,平面的法向量,
所以,所以,
所以或,
故答案为:或.
18.(1)证明见解析;(2).
(1)取中点,连接,,证明平面即可;
(2)首先证明平面,然后以射线,,为,,正半轴建系,然后算出和平面的法向量即可得到答案.
【详解】
(1)取中点,连接,,因为,,
所以,,又因为,所以平面,
即.
(2)由(1)得,平面,又因为平面,
所以平面平面,
易得,,所以,即,
又因为平面平面,所以平面,
如图所示,以射线,,为,,正半轴建系,
,,,,,
,,,
设为平面一个法向量,则有,取,
设为直线与平面所成角,则.
即直线与平面所成角的正弦值为.
19.(1);(2);
根据题目信息建立空间直角坐标系,
(1)将直线的方向向量表示出来,根据数量积等于0求解题目中的取值,进而可以求得,最后获得体积之比;
(2)分别将两个平面的法向量求解出来,根据面面角的公式求解平面角的余弦值,最后根据角是钝角得出结果即可.
【详解】
(1)取的中点为,
因为即,所以,
所以,又因为平面平面,
平面平面,
所以平面,
连接,由题意可知,
以点为坐标原点,分别以为轴建立空间直角坐标系,
则,,,,
所以,,
因为,所以,
解得:或者(舍);
因为三棱锥和四棱锥的体积分别为,,
所以.
(2) 二面角是定值,证明如下:
由(1)知,面的法向量,
由,,
设面的法向量为 ,
所以,
取,则,,即,
设二面角的平面角为,
所以,
由图可知二面角的平面角为钝角,
所以二面角的平面角的余弦值为.
用向量方法解决立体几何问题,树立“基底”意识,利用基向量进行线性运算,要理解空间向量概念、性质、运算,注意和平面向量类比.
20.(1)证明见解析;(2);(3)2.
(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,由此能证明PB∥平面ACM.
(2)求出平面CDP的法向量和平面ACD的法向量,利用向量法能求出二面角A﹣CD﹣P的正弦值.
(3)求出平面CDP的法向量,由直线AM与平面PCD所成角的正弦值为,利用向量法能求出MD的长.
【详解】
(1)证明:∵在四棱锥P﹣ABCD中,
PA⊥平面ABCD,AB⊥AD,BC∥AD,
∴以A为原点,AB为x轴,AD为y轴,AP为z轴,
建立空间直角坐标系,
∵点M是棱PD上一点,PM:MD=1:2,
AB=BC=2,AD=PA=4.
∴P(0,0,4),A(0,0,0),B(2,0,0),
C(2,2,0),M(0,,),
=(2,0,﹣4),=(2,2,0),=(0,,),
设平面ACM的法向量,
则,取x=2,得(2,﹣2,1),
∵4﹣4=0,PB 平面ACM,∴PB∥平面ACM.
(2)D(0,4,0),=(2,2,﹣4),=(0,4,﹣4),
设平面CDP的法向量(a,b,c),
则,取b=1,得(1,1,1),
平面ACD的法向量(0,0,1),
设二面角A﹣CD﹣P的平面角为θ,
则|cosθ|==,
∴二面角A﹣CD﹣P的正弦值为=.
(3)设,(0≤λ≤1),
则,
∴,
,平面CDP的法向量,
∵直线AM与平面PCD所成角的正弦值为,
∴| |===,
解得λ=,
∴.
21.(1)证明见解析;(2).
(1)建立空间直角坐标系,利用向量法证得平面.
(2)利用直线的方向向量,平面的法向量,计算线面角的正弦值.
【详解】
(1)以为原点建立如图所示空间直角坐标系,则
.
,
,所以,
由于,所以平面.
(2),
,
设平面的法向量为,则
,令,则,所以.
设直线与平面所成角为,则
.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在空间直角坐标系内,平面经过三点,向量是平面的一个法向量,则( )
A. B. C.5 D.7
2.如图,在底面为正方形的四棱锥P-ABCD中,已知PA⊥平面ABCD,且PA=.若点M为PD中点,则直线CM与PB所成角的大小为( )
A.60° B.45° C.30° D.90°
3.如图,在三棱锥中,为等边三角形,为等腰直角三角形,,平面平面,为的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
4.已知正四棱锥,侧棱长是底面边长的2倍,是的中点,则所成的角的余弦值为( )
A. B. C. D.
5.二面角--为60°,A、B是棱上的两点,、分别在半平面内,,,且,,则的长为( )
A. B. C. D.
6.已知四边形ABCD为正方形,P为平面ABCD外一点,PD⊥AD,PD=AD=2,二面角P-AD-C为60°,则P到AB的距离是( )
A.2 B.
C.2 D.
7.若O为坐标原点, =(1,1,-2),=(3,2,8),=(0,1,0),则线段AB的中点P到点C的距离为( )
A. B.
C. D.
8.已知,,则平面ABC的一个单位法向量为( )
A. B.
C. D.
9.如图,在三棱锥中,已知,,平面平面,则异面直线与所成角的余弦值为( )
A. B. C. D.
10.在棱长为的正方体中,是的中点,则点到平面的距离是( )
A. B. C. D.
11.直三棱柱ABC-A1B1C1中,△ABC为等边三角形, AA1=AB,M是A1C1的中点,则AM与平面所成角的正弦值为( )
A. B. C. D.
12.若平面α,β的法向量分别为,,则下列结论中正确的是( )
A. B.α,β相交但不垂直
C. D.或α,β重合
二、填空题
13.若向量是直线l的方向向量,向量是平面α的法向量,则直线l与平面α所成的角为______.
14.如图,四棱柱的底面是正方形,为底面中心,平面,.平面的法向量________.
15.如图所示,已知点P为菱形ABCD外一点,且平面ABCD,,点F为PC的中点,则二面角的正切值为__________
16.已知向量是直线l的一个方向向量,向量是平面的一个法向量,若直线平面,则实数m的值为______.
17.若直线的方向向量为,平面的法向量,则直线与平面的位置关系是___________________.
三、解答题
18.在三棱锥中,,,.
(1)求证:;
(2)若为上一点,且,求直线与平面所成角的正弦值.
19.如图1,菱形中,动点,在边,上(不含端点),且存在实数使,沿将向上折起得到,使得平面平面,如图2所示.
(1)若,设三棱锥和四棱锥的体积分别为,,求;
(2)试讨论,当点的位置变化时,二面角是否为定值,若是,求出该二面角的余弦值,若不是,说明理由.
20.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AB⊥AD,BC∥AD,点M是棱PD上一点,且AB=BC=2,AD=PA=4.
(1)若PM:MD=1:2,求证:PB∥平面ACM;
(2)求二面角A﹣CD﹣P的正弦值;
(3)若直线AM与平面PCD所成角的正弦值为,求MD的长.
21.如图,已知平面,底面为正方形,,分别为的中点.
(1)求证:平面;
(2)求与平面所成角的正弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
求出,,利用与数量积为0,求解即可.
【详解】
,
可得,,
故选:D
2.C
以为坐标原点建立空间直角坐标系,求出,,利用向量法即可求出.
【详解】
如图所示:以为坐标原点,以,,为单位向量建立空间直角坐标系,
设,则,,,,,
故,,
故,
由异面直线夹角的范围是,故直线与所成角的大小为.
故选:C.
3.B
取的中点,连接,根据等腰三角形的性质以及面面垂直的性质证明两两垂直,以为坐标原点,建立如图所示的空间直角坐标系,求出各点坐标以及和的坐标,由空间向量夹角公式计算即可求解.
【详解】
取的中点,连接,因为,所以
又因为平面平面,平面平面,面,
所以平面,
又因为,,可得两两垂直,
所以以为坐标原点,建立如图所示的空间直角坐标系,
因为是等腰直角三角形,,为等边三角形,
可得,,,,
所以,,
所以,
设异面直线与所成角为,则
所以异面直线与所成角的余弦值为,
故选:B.
4.C
建立空间直角坐标系,利用空间向量法求出异面直线所成角的余弦值.
【详解】
解:如图所示建立空间直角坐标系,
不妨设,则,,所以
,,, ,, .
.
与所成角的余弦值为.
故选:.
5.D
由已知条件和空间向量加法可得,再根据向量模和数量积的关系可得 ,由此能求出的长.
【详解】
因为二面角--为60°,A、B是棱上的两点,、分别在半平面内,,,
所以,,
又
所以
.
所以的长为.
故选:D.
本题考查空间线段长的求法,是中档题,解题时要认真审题,注意向量法的合理运用.
6.D
先作出P到AB的距离PE,再解三角形求出PE.
【详解】
因为ABCD为正方形,所以AD⊥DC.
由 ∠PDC为二面角P-AD-C的平面角,即∠PDC=60°.
如图所示,过P作PH⊥DC于H.
∵,∴AD⊥面PDC.,∴AD⊥面PH.
又PH⊥DC, ,∴PH⊥面ABCD,
在平面AC内过H作HE⊥AB于E,连接PE,则PE⊥AB,
所以线段PE即为所求.
以H为坐标原点建立空间直角坐标系,
则
所以,∴
故选:D.
方法点睛:
距离的计算方法有两类:
(1)几何法:利用几何图形求值;
(2)向量法:把距离用向量表示出来,转化为代数计算.
7.D
先求出的坐标,再利用三角形减法法则求的坐标,再求||即得解.
【详解】
由题意= (+)=,=-=,||=.
故答案为D
本题主要考查向量的坐标运算,考查向量的三角形法则和平行四边形法则,考查向量的模的计算,意在考查学生对这些知识的掌握水平和分析推理能力.
8.B
设平面的法向量为,进而得,再根据为单位向量即可得答案.
【详解】
设平面的法向量为,
则有取,则.
所以.因为,
所以平面的一个单位法向量可以是.
故选:B
本题考查平面的法向量的求法,考查运算求解能力,解题得关键在于掌握单位向量的表示形式,是中档题.
9.A
取的中点为,连接,证明平面,,然后建立空间直角坐标系,利用向量求解即可.
【详解】
取的中点为,连接
因为,所以,
因为平面平面,平面平面,平面
所以平面
因为,
所以
如图建立空间直角坐标系,则
所以
所以异面直线与所成角的余弦值为
故选:A
10.A
以为空间直角坐标原点建立空间直角坐标系,通过点面距离公式,计算点到平面的距离.
【详解】
以为空间直角坐标原点,分别为轴建立空间直角坐标系.由于是中点,故,且,设是平面的法向量,故,故可设,故到平面的距离.故选A.
本小题主要考查利用空间向量计算点到面的距离.计算过程中要先求得平面的法向量.属于基础题.
11.B
取的中点,以为原点,所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,即可根据线面角的向量公式求出.
【详解】
如图所示,取的中点,以为原点,所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
不妨设,则,
所以,平面的一个法向量为
设AM与平面所成角为,向量与所成的角为,
所以,
即AM与平面所成角的正弦值为.
故选:B.
12.D
根据题意,结合面面位置关系的向量证明,即可求解.
【详解】
根据题意,易知,故平面α,β的法向量共线,因此或α,β重合.
故选:D.
13.##
直接利用向量的夹角公式求解即可
【详解】
设直线l与平面α所成的角为,则由题意得
,
因为,
所以,
所以直线l与平面α所成的角为,
故答案为:
14.(答案不唯一)
易知,,从而可得,结合,,从而解得
【详解】
是正方形,且,
,
,
,,
,
,
,,
,
故,
故,
∵向量是平面OCB1的法向量,
,
,
故,,取,故,
平面的法向量
故答案为:(答案不唯一)
本题考查平面的法向量,建系求解即可,主要考查学生的运算能力,属于基础题.
15.
分析空间几何体的特征,建立合适的空间直角坐标系,用空间向量求二面角的余弦值,再求正切值﹒
【详解】
如图所示,连接BD,,连接OF,
以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴建立空间直角坐标系Oxyz.
设,则.
所以,,,.
结合图形可知,,且为平面BOF的法向量,
由,,
可求得平面BCF的一个法向量为.
所以,,
所以.
故答案为:
16.-2
由已知可得,即,计算即可得出结果.
【详解】
因为是直线的一个方向向量,是平面的一个法向量,且直线平面,所以,
所以,解得.
故答案为:-2.
17.或
由空间向量数量积的坐标表示可得,再由线面位置关系即可求解.
【详解】
因为直线的方向向量为,平面的法向量,
所以,所以,
所以或,
故答案为:或.
18.(1)证明见解析;(2).
(1)取中点,连接,,证明平面即可;
(2)首先证明平面,然后以射线,,为,,正半轴建系,然后算出和平面的法向量即可得到答案.
【详解】
(1)取中点,连接,,因为,,
所以,,又因为,所以平面,
即.
(2)由(1)得,平面,又因为平面,
所以平面平面,
易得,,所以,即,
又因为平面平面,所以平面,
如图所示,以射线,,为,,正半轴建系,
,,,,,
,,,
设为平面一个法向量,则有,取,
设为直线与平面所成角,则.
即直线与平面所成角的正弦值为.
19.(1);(2);
根据题目信息建立空间直角坐标系,
(1)将直线的方向向量表示出来,根据数量积等于0求解题目中的取值,进而可以求得,最后获得体积之比;
(2)分别将两个平面的法向量求解出来,根据面面角的公式求解平面角的余弦值,最后根据角是钝角得出结果即可.
【详解】
(1)取的中点为,
因为即,所以,
所以,又因为平面平面,
平面平面,
所以平面,
连接,由题意可知,
以点为坐标原点,分别以为轴建立空间直角坐标系,
则,,,,
所以,,
因为,所以,
解得:或者(舍);
因为三棱锥和四棱锥的体积分别为,,
所以.
(2) 二面角是定值,证明如下:
由(1)知,面的法向量,
由,,
设面的法向量为 ,
所以,
取,则,,即,
设二面角的平面角为,
所以,
由图可知二面角的平面角为钝角,
所以二面角的平面角的余弦值为.
用向量方法解决立体几何问题,树立“基底”意识,利用基向量进行线性运算,要理解空间向量概念、性质、运算,注意和平面向量类比.
20.(1)证明见解析;(2);(3)2.
(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,由此能证明PB∥平面ACM.
(2)求出平面CDP的法向量和平面ACD的法向量,利用向量法能求出二面角A﹣CD﹣P的正弦值.
(3)求出平面CDP的法向量,由直线AM与平面PCD所成角的正弦值为,利用向量法能求出MD的长.
【详解】
(1)证明:∵在四棱锥P﹣ABCD中,
PA⊥平面ABCD,AB⊥AD,BC∥AD,
∴以A为原点,AB为x轴,AD为y轴,AP为z轴,
建立空间直角坐标系,
∵点M是棱PD上一点,PM:MD=1:2,
AB=BC=2,AD=PA=4.
∴P(0,0,4),A(0,0,0),B(2,0,0),
C(2,2,0),M(0,,),
=(2,0,﹣4),=(2,2,0),=(0,,),
设平面ACM的法向量,
则,取x=2,得(2,﹣2,1),
∵4﹣4=0,PB 平面ACM,∴PB∥平面ACM.
(2)D(0,4,0),=(2,2,﹣4),=(0,4,﹣4),
设平面CDP的法向量(a,b,c),
则,取b=1,得(1,1,1),
平面ACD的法向量(0,0,1),
设二面角A﹣CD﹣P的平面角为θ,
则|cosθ|==,
∴二面角A﹣CD﹣P的正弦值为=.
(3)设,(0≤λ≤1),
则,
∴,
,平面CDP的法向量,
∵直线AM与平面PCD所成角的正弦值为,
∴| |===,
解得λ=,
∴.
21.(1)证明见解析;(2).
(1)建立空间直角坐标系,利用向量法证得平面.
(2)利用直线的方向向量,平面的法向量,计算线面角的正弦值.
【详解】
(1)以为原点建立如图所示空间直角坐标系,则
.
,
,所以,
由于,所以平面.
(2),
,
设平面的法向量为,则
,令,则,所以.
设直线与平面所成角为,则
.
答案第1页,共2页
答案第1页,共2页
