人教版数学六年级下册第六单元整理复习2 课件(21张PPT)
文档属性
| 名称 | 人教版数学六年级下册第六单元整理复习2 课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 751.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 16:40:54 | ||
图片预览






文档简介
(共21张PPT)
*
回答下面的问题,并列出算式:
一个圆柱形无盖的水桶,底面半径10分米,高20分米。
1.给这个水桶加个箍,是求什么?
2.求这个水桶的占地面积,是求什么?
3.做这样一个水桶用多少铁皮,是求什么?
4.这个水桶能装多少水,是求什么?
基本练习:
2×3.14×10
3.14×102
3.14×102+2×3.14×10×20
3.14×102×20
(底面周长)
(底面积)
(表面积)
(容积)
1.下面( )图形是圆柱的展开图。(单位:cm)
一、基本练习
关键是应满足:长方形的长等于圆的底面周长。
C=πd
=3.14×3
=9.42 cm
A
2.填空。
(1)一个圆柱和一个圆锥等底等高,圆锥的体积比圆柱的体积少1.2立方分米,那么圆锥的体积是( )立方分米,圆柱的体积是( )立方分米。
0.6
1.8
(2)把一个圆柱体木块削成一个最大的圆锥体,要削去30立方分米,未削前圆柱的体积是( )立方分米
45
(3)一个圆柱体和一个圆锥体的底面积和体积都相等,圆柱的高0.6厘米,圆锥的高是( )厘米。
1.8
*
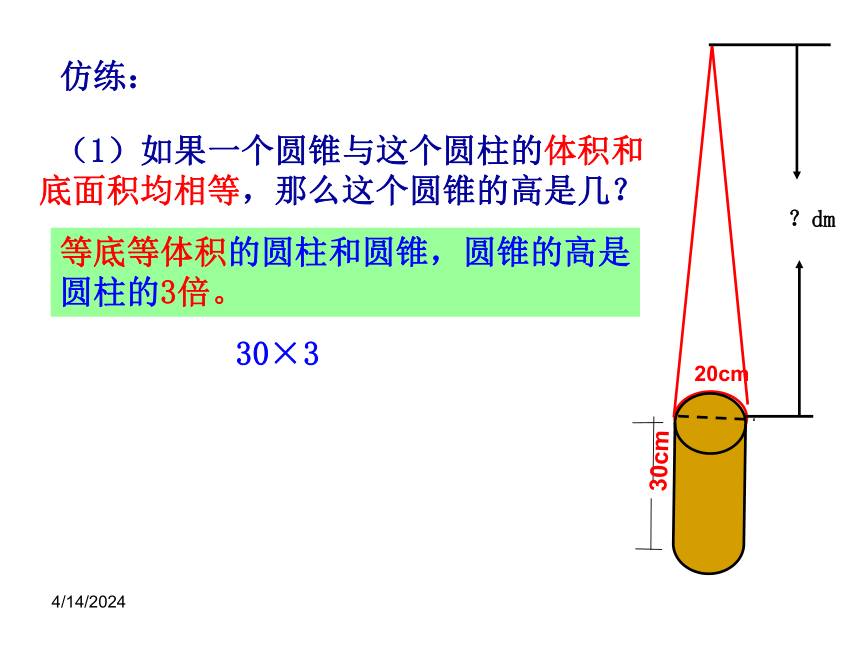
?dm
20cm
30cm
30×3
等底等体积的圆柱和圆锥,圆锥的高是圆柱的3倍。
(1)如果一个圆锥与这个圆柱的体积和底面积均相等,那么这个圆锥的高是几?
仿练:
*
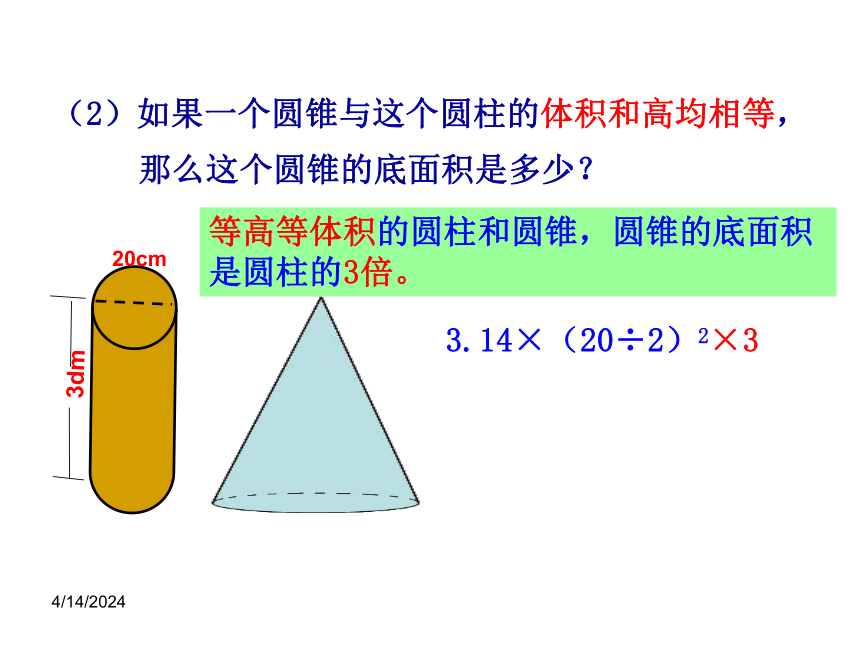
(2)如果一个圆锥与这个圆柱的体积和高均相等,那么这个圆锥的底面积是多少?
20cm
3dm
等高等体积的圆柱和圆锥,圆锥的底面积是圆柱的3倍。
3.14×(20÷2)2×3
(2)圆柱底面半径扩大2倍,高不变,它的侧面积就扩大4倍。( )
(3)圆锥底面积不变,它的高度越高,圆锥的体积就越大。( )
(4)如果圆锥的体积是圆柱体积的1/3,那么这个圆锥和圆柱一定等底等高。( )
(5)两个体积相等的圆柱和圆锥,它们的底面积也相等。圆柱的高一定是圆锥高的1/3。 ( )
(6)一个圆锥的底面半径不变,高扩大2倍,体积就扩大2倍。 ( )
(1)因为圆柱体积是圆锥体积的3倍,所以圆锥体积都比圆柱体积小。 ( )
3.判断。
×
×
体积扩大4倍
√
×
√
√
二、综合练习
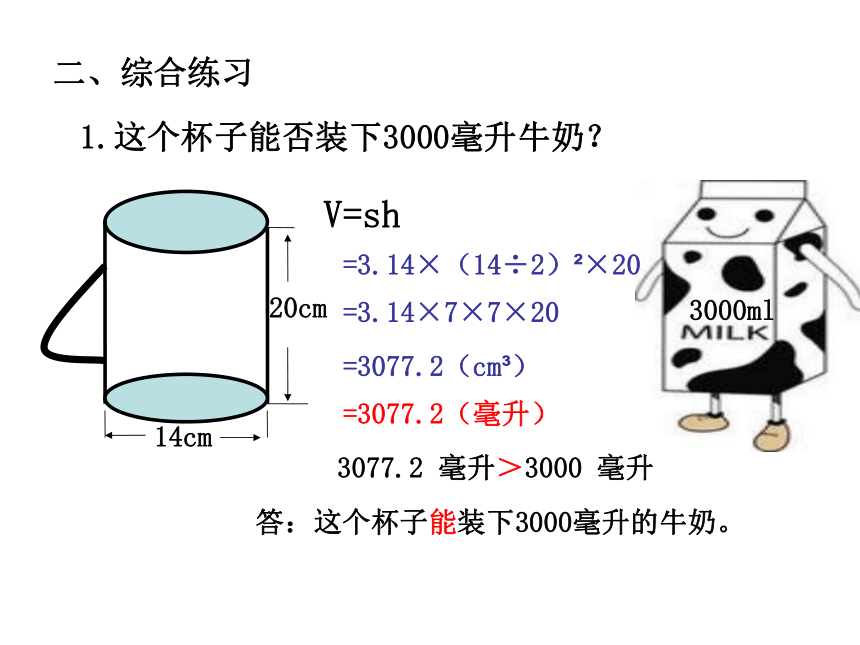
1.这个杯子能否装下3000毫升牛奶?
14cm
20cm
3000ml
V=sh
=3.14×(14÷2) ×20
=3.14×7×7×20
=3077.2(cm )
=3077.2(毫升)
3077.2 毫升>3000 毫升
答:这个杯子能装下3000毫升的牛奶。
2.一个装满稻谷的圆柱形粮囤,底面面积为2平方米,高为80厘米。
(1)你知道这个粮囤的体积是多少立方米?
(2)如果每立方米稻谷约重600千克,这个粮囤的稻谷约重多少千克?
V=sh
=2×0.8
80厘米=0.8米
=1.6(m )
1.6×600=960(千克)
3.在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)
先求圆锥的体积,再求沙的重量
V= sh
1
3
= ×3.14×(4÷2) ×1.5
=3.14×4×0.5
1
3
0.5
=6.28(m )
6.28×1.7=10.676(吨)
1
≈11(吨)
4.一个空心石圆柱如右图。
(1)石柱的实际体积是多少立方分米?
(2)这种石柱每立方分米重3千克。这个石柱的重量大约是多少吨?
V=s环h
=3.14×(3 -1 )×16
=3.14×8×16
=401.92(立方分米)
401.92×3=1205.76(千克)
=1.20576(吨)
5.你能求出下图中的圆柱形钢坯的高吗?如果铸造成圆锥呢?
31.4cm
10cm
20cm
长方体钢坯铸造成圆形钢柱
20cm
铸造(熔铸) 说明体积不变
长方体的体积 = 圆柱的体积
V=abh
h=V÷s
=31.4×10×20
=6280(cm )
=6280÷[3.14×(20÷2) ]
=6280÷314
=20(cm)
6.一瓶葡萄酒,瓶子的容积是1000立方厘米,瓶子中酒高14厘米。小强把瓶子倒过来,这时瓶底中空出的高度为6厘米。你能求出瓶中有多少立方厘米的葡萄酒吗?
14㎝
6㎝
h: 14+6=20(厘米)
S=V÷h
=1000÷20
=50(平方厘米)
V=Sh
=50×14
=700(立方厘米)
*
20cm
30cm
(1)如图,把这根木头横着放,滚动一圈,滚动的面积是多少?
3.14×20×30=1884(平方厘米)
6.比较练习。
*
20cm
30cm
(2)把这根木头全都刷上油漆,刷油漆的面积有多大?
3.14×20×30+ 3.14×(20÷2)2×2
=1884 + 628
=2512(平方厘米)
*
(3)这个木头的体积是多少?
3.14×(20÷2)2 ×30
=3.14 ×3000
=9420(立方分米)
20cm
30cm
*
(4)把这个圆柱形的木头削成最大的圆锥,这个圆锥形的体积是多少?削去的体积是多少?
20cm
30cm
V= Sh
= ×3.14×(20÷2)×30
2
1
3
削成的圆锥与圆柱等底等高。
削去部分的体积是圆柱体积的( )。
2
3
3.14×(20÷2)2×30
×
2
3
*
(5)如果沿着底面直径把这个圆柱切开,那么,它的表面积增加了多少 ?
20cm
30cm
切面的长等于圆柱直径,
切面的宽等于圆柱的高。
20×30×2
=1200(平方厘米)
表面积增加了两个纵切面。
*
(6)把这个圆柱切成四段,它的表面积增加了多少?
20cm
30cm
切成四段,说明切了3下,表面积增加了6个横切面。
一个横切面相当于一个底面。
3.14×(20÷2)2×6
*
(7)如果截去4厘米高的一截,它的表面积会有什么变化呢?
20cm
30cm
表面积减少了,减少了截去部分的侧面积
3.14×20×4
*
*
(8)如果木头浮在水面上,正好一半露出水面,这根木头与水接触面的面积是多少?
3.14×20×30÷2=942(平方厘米)
3.14×10 =314(平方厘米)
942+314=1256(平方厘米)
侧面积的一半 + 一个底面
20
30
*
回答下面的问题,并列出算式:
一个圆柱形无盖的水桶,底面半径10分米,高20分米。
1.给这个水桶加个箍,是求什么?
2.求这个水桶的占地面积,是求什么?
3.做这样一个水桶用多少铁皮,是求什么?
4.这个水桶能装多少水,是求什么?
基本练习:
2×3.14×10
3.14×102
3.14×102+2×3.14×10×20
3.14×102×20
(底面周长)
(底面积)
(表面积)
(容积)
1.下面( )图形是圆柱的展开图。(单位:cm)
一、基本练习
关键是应满足:长方形的长等于圆的底面周长。
C=πd
=3.14×3
=9.42 cm
A
2.填空。
(1)一个圆柱和一个圆锥等底等高,圆锥的体积比圆柱的体积少1.2立方分米,那么圆锥的体积是( )立方分米,圆柱的体积是( )立方分米。
0.6
1.8
(2)把一个圆柱体木块削成一个最大的圆锥体,要削去30立方分米,未削前圆柱的体积是( )立方分米
45
(3)一个圆柱体和一个圆锥体的底面积和体积都相等,圆柱的高0.6厘米,圆锥的高是( )厘米。
1.8
*
?dm
20cm
30cm
30×3
等底等体积的圆柱和圆锥,圆锥的高是圆柱的3倍。
(1)如果一个圆锥与这个圆柱的体积和底面积均相等,那么这个圆锥的高是几?
仿练:
*
(2)如果一个圆锥与这个圆柱的体积和高均相等,那么这个圆锥的底面积是多少?
20cm
3dm
等高等体积的圆柱和圆锥,圆锥的底面积是圆柱的3倍。
3.14×(20÷2)2×3
(2)圆柱底面半径扩大2倍,高不变,它的侧面积就扩大4倍。( )
(3)圆锥底面积不变,它的高度越高,圆锥的体积就越大。( )
(4)如果圆锥的体积是圆柱体积的1/3,那么这个圆锥和圆柱一定等底等高。( )
(5)两个体积相等的圆柱和圆锥,它们的底面积也相等。圆柱的高一定是圆锥高的1/3。 ( )
(6)一个圆锥的底面半径不变,高扩大2倍,体积就扩大2倍。 ( )
(1)因为圆柱体积是圆锥体积的3倍,所以圆锥体积都比圆柱体积小。 ( )
3.判断。
×
×
体积扩大4倍
√
×
√
√
二、综合练习
1.这个杯子能否装下3000毫升牛奶?
14cm
20cm
3000ml
V=sh
=3.14×(14÷2) ×20
=3.14×7×7×20
=3077.2(cm )
=3077.2(毫升)
3077.2 毫升>3000 毫升
答:这个杯子能装下3000毫升的牛奶。
2.一个装满稻谷的圆柱形粮囤,底面面积为2平方米,高为80厘米。
(1)你知道这个粮囤的体积是多少立方米?
(2)如果每立方米稻谷约重600千克,这个粮囤的稻谷约重多少千克?
V=sh
=2×0.8
80厘米=0.8米
=1.6(m )
1.6×600=960(千克)
3.在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)
先求圆锥的体积,再求沙的重量
V= sh
1
3
= ×3.14×(4÷2) ×1.5
=3.14×4×0.5
1
3
0.5
=6.28(m )
6.28×1.7=10.676(吨)
1
≈11(吨)
4.一个空心石圆柱如右图。
(1)石柱的实际体积是多少立方分米?
(2)这种石柱每立方分米重3千克。这个石柱的重量大约是多少吨?
V=s环h
=3.14×(3 -1 )×16
=3.14×8×16
=401.92(立方分米)
401.92×3=1205.76(千克)
=1.20576(吨)
5.你能求出下图中的圆柱形钢坯的高吗?如果铸造成圆锥呢?
31.4cm
10cm
20cm
长方体钢坯铸造成圆形钢柱
20cm
铸造(熔铸) 说明体积不变
长方体的体积 = 圆柱的体积
V=abh
h=V÷s
=31.4×10×20
=6280(cm )
=6280÷[3.14×(20÷2) ]
=6280÷314
=20(cm)
6.一瓶葡萄酒,瓶子的容积是1000立方厘米,瓶子中酒高14厘米。小强把瓶子倒过来,这时瓶底中空出的高度为6厘米。你能求出瓶中有多少立方厘米的葡萄酒吗?
14㎝
6㎝
h: 14+6=20(厘米)
S=V÷h
=1000÷20
=50(平方厘米)
V=Sh
=50×14
=700(立方厘米)
*
20cm
30cm
(1)如图,把这根木头横着放,滚动一圈,滚动的面积是多少?
3.14×20×30=1884(平方厘米)
6.比较练习。
*
20cm
30cm
(2)把这根木头全都刷上油漆,刷油漆的面积有多大?
3.14×20×30+ 3.14×(20÷2)2×2
=1884 + 628
=2512(平方厘米)
*
(3)这个木头的体积是多少?
3.14×(20÷2)2 ×30
=3.14 ×3000
=9420(立方分米)
20cm
30cm
*
(4)把这个圆柱形的木头削成最大的圆锥,这个圆锥形的体积是多少?削去的体积是多少?
20cm
30cm
V= Sh
= ×3.14×(20÷2)×30
2
1
3
削成的圆锥与圆柱等底等高。
削去部分的体积是圆柱体积的( )。
2
3
3.14×(20÷2)2×30
×
2
3
*
(5)如果沿着底面直径把这个圆柱切开,那么,它的表面积增加了多少 ?
20cm
30cm
切面的长等于圆柱直径,
切面的宽等于圆柱的高。
20×30×2
=1200(平方厘米)
表面积增加了两个纵切面。
*
(6)把这个圆柱切成四段,它的表面积增加了多少?
20cm
30cm
切成四段,说明切了3下,表面积增加了6个横切面。
一个横切面相当于一个底面。
3.14×(20÷2)2×6
*
(7)如果截去4厘米高的一截,它的表面积会有什么变化呢?
20cm
30cm
表面积减少了,减少了截去部分的侧面积
3.14×20×4
*
*
(8)如果木头浮在水面上,正好一半露出水面,这根木头与水接触面的面积是多少?
3.14×20×30÷2=942(平方厘米)
3.14×10 =314(平方厘米)
942+314=1256(平方厘米)
侧面积的一半 + 一个底面
20
30
