必修第二册9.2用样本估计总体 同步练习(Word版含解析)
文档属性
| 名称 | 必修第二册9.2用样本估计总体 同步练习(Word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览



文档简介
人教A版(2019)必修第二册 9.2 用样本估计总体 同步练习
一、单选题
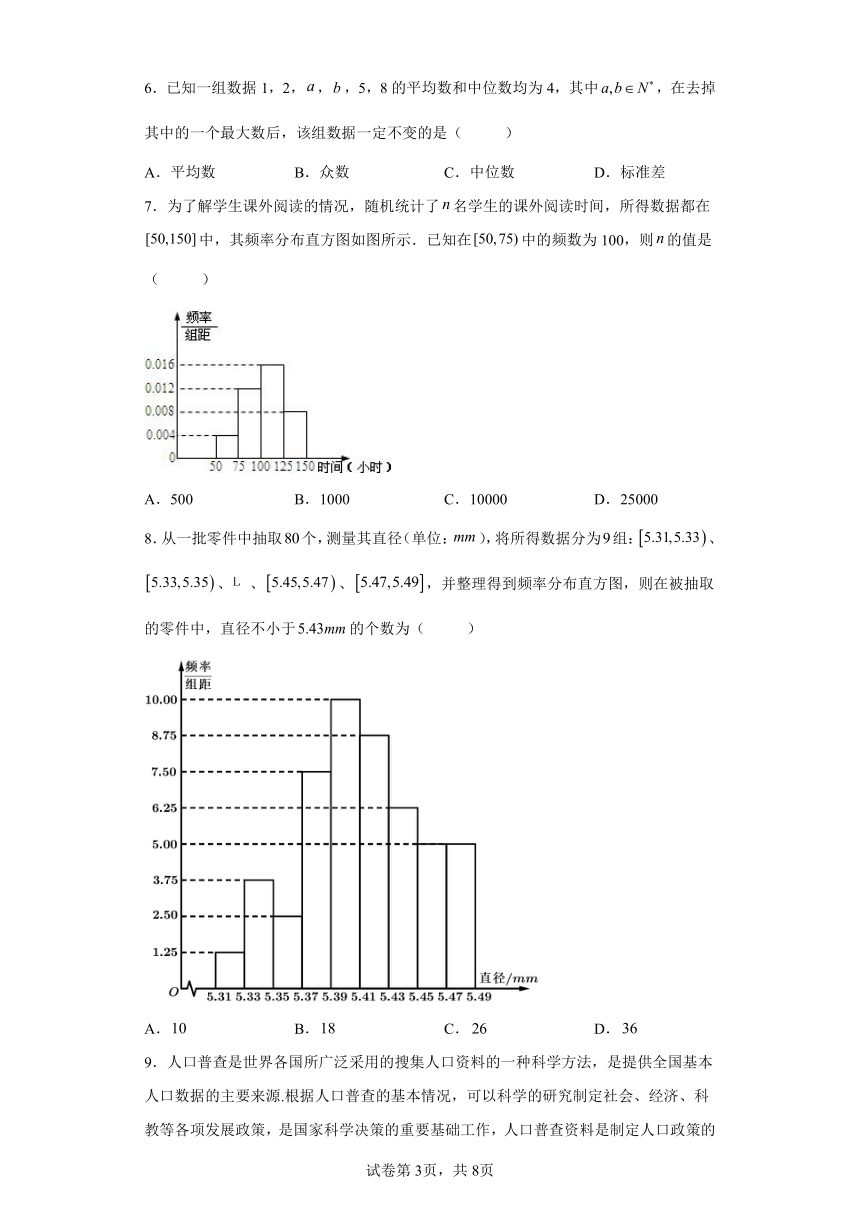
1.为了增强大学生的环保意识,加强对“碳中和”概念的宣传,某公益组织分别在两所大学随机选取10名学生进行环保问题测试(满分100分),这20名学生得分的折线图如图所示,关于这两所学校被选取的学生的得分,下列结论错误的是( )
A.校学生分数的平均分大于校学生分数的平均分
B.校学生分数的众数大于校学生分数的众数
C.校学生分数的中位数等于校学生分数的中位数
D.校学生分数的方差大于校学生分数的方
2.安徽省统计局2020年11月20日发布了全省规模以上工业增加值同比增长速度(注:增加值增长速度均为扣除价格因素的实际增长率,同比是指在相邻时段内某一相同时间点进行比较),如下折线统计图所示,则下列说法正确的是( )
A.2020年3月份到10月份,工业增加值同比有增加也有下降
B.2020年3月份到10月份,工业增加值同比增加速度最大的是8月
C.2020年10月工业增加值同比下降
D.2020年10月工业增加值同比增长
3.在某次测量中得到的样本数据如下17,22,37,42,31,58,61,若B样本数据恰好是样本数据都减2后所得数据,则,两样本的下列数字特征对应相同的是( )
A.平均数 B.众数 C.中位数 D.方差
4.第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法错误的是( )
A.第一场得分的中位数为 B.第二场得分的平均数为
C.第一场得分的极差大于第二场得分的极差 D.第一场与第二场得分的众数相等
5.下表为12名毕业生的起始月薪:
毕业生 起始月薪 毕业生 起始月薪
1 2850 7 2890
2 2950 8 3130
3 3050 9 2940
4 2880 10 3325
5 2755 11 2920
6 2710 12 2880
根据表中所给的数据计算第85百分位数为( )A.2710 B.2890 C.3130 D.2940
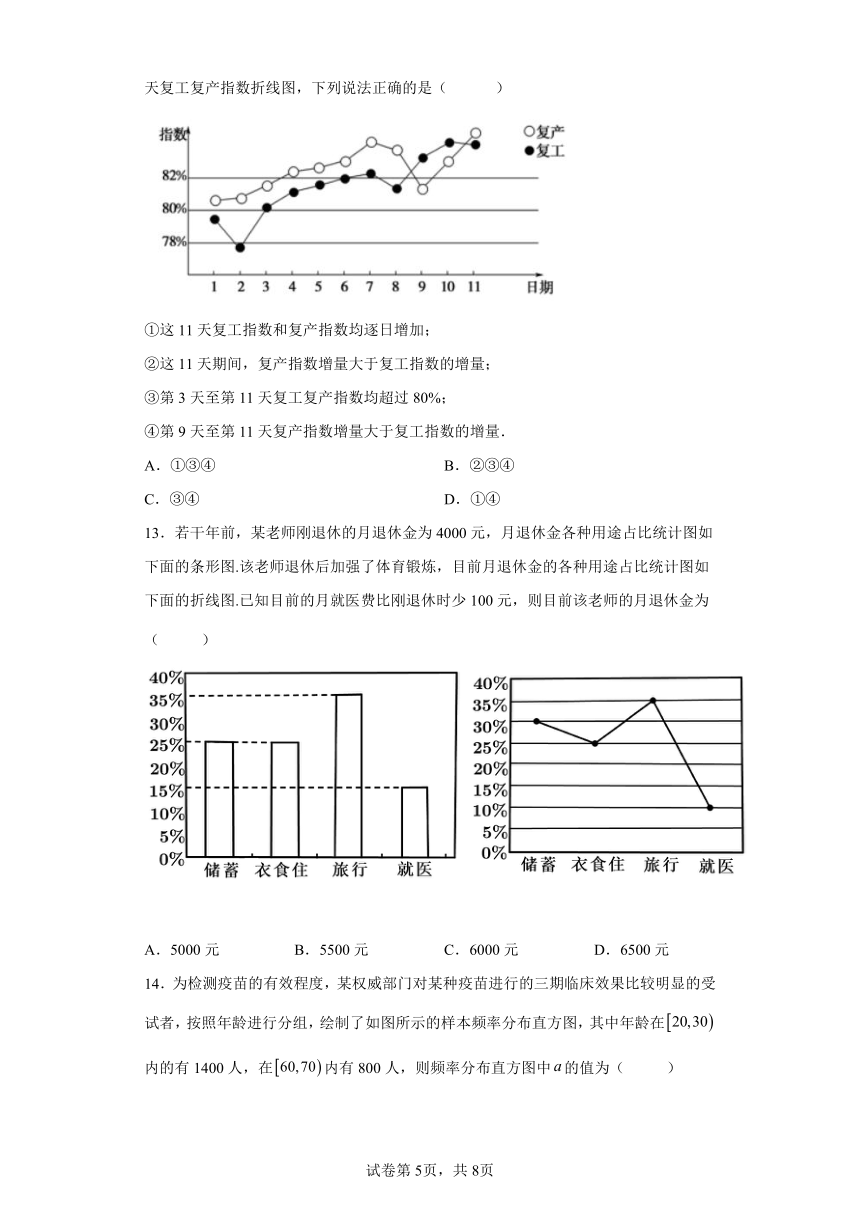
6.已知一组数据1,2,,,5,8的平均数和中位数均为4,其中,在去掉其中的一个最大数后,该组数据一定不变的是( )
A.平均数 B.众数 C.中位数 D.标准差
7.为了解学生课外阅读的情况,随机统计了名学生的课外阅读时间,所得数据都在中,其频率分布直方图如图所示.已知在中的频数为100,则的值是( )
A.500 B.1000 C.10000 D.25000
8.从一批零件中抽取个,测量其直径(单位:),将所得数据分为组:、、、、,并整理得到频率分布直方图,则在被抽取的零件中,直径不小于的个数为( )
A. B. C. D.
9.人口普查是世界各国所广泛采用的搜集人口资料的一种科学方法,是提供全国基本人口数据的主要来源.根据人口普查的基本情况,可以科学的研究制定社会、经济、科教等各项发展政策,是国家科学决策的重要基础工作,人口普查资料是制定人口政策的依据和前提.截止2020年10月10日,我国共进行了六次人口普查,下图是这六次人口普查的人数和增幅情况,下列说法正确的是( )
A.人口数逐次增加,第二次增幅最大 B.第六次普查人数最多,第四次增幅最小
C.第六次普查人数最多,第三次增幅最大 D.人口数逐次增加,从第二次开始增幅减小
10.一组数据中的每一个数据都乘以3,再减去50,得到一组新数据,若求得新的数据的平均数是1.6,方差是3.6,则原来数据的平均数和方差分别是( )
A.17.2,3.6 B.54.8,3.6 C.17.2,0.4 D.54.8,0.4
11.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
12.我国新冠肺炎疫情防控进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
①这11天复工指数和复产指数均逐日增加;
②这11天期间,复产指数增量大于复工指数的增量;
③第3天至第11天复工复产指数均超过80%;
④第9天至第11天复产指数增量大于复工指数的增量.
A.①③④ B.②③④
C.③④ D.①④
13.若干年前,某老师刚退休的月退休金为4000元,月退休金各种用途占比统计图如下面的条形图.该老师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该老师的月退休金为( )
A.5000元 B.5500元 C.6000元 D.6500元
14.为检测疫苗的有效程度,某权威部门对某种疫苗进行的三期临床效果比较明显的受试者,按照年龄进行分组,绘制了如图所示的样本频率分布直方图,其中年龄在内的有1400人,在内有800人,则频率分布直方图中的值为( )
A.0.008 B.0.08 C.0.006 D.0.06
15.已知一组数据,,的平均数是5,方差是4则由,,,11这4个数据组成的新的一组数据的方差是( )
A.16 B.14 C.12 D.8
二、填空题
16.甲组数据为,乙组数据为,则甲、乙两组数据的平均数、极差及中位数相同的是_________
17.某测试卷的满分为100分,60分及以上为及格.现有100人参加测试,将这100人的卷面分数按照,,,分组后绘制的频率分布直方图如图所示.由于及格人数较少,某位老师准备将每位学生的卷面得分采用“开方乘以10取整”的方法进行换算以提高及格率(实数a的取整为不超过a的最大整数),如:某位学生卷面得分为49分,则换算成70分作为最终考试成绩,则按照这种方法求出的及格率与实际及格率的差是______.
18.A工厂年前加紧手套生产,设该工厂连续5天生产的手套数依次为x1,x2,x3,x4,x5(单位:万只),若这组数据x1,x2,x3,x4,x5的方差为1.44,且x12,x22,x32,x42,x52的平均数为4,则该工厂这5天平均每天生产手套___________万只.
三、解答题
19.现有银川二中高一年级某班甲、乙两名学生自进入高中以来的历次数学成绩(单位:分),具体考试成绩如下:
甲:、、、、、、、、、、、、;
乙:、、、、、、、、、、、、.
(1)请你画出两人数学成绩的茎叶图;
(2)根据茎叶图,运用统计知识对两人的成绩进行比较.(最少写出两条统计结论)
20.一次数学知识竞赛中,两组学生成绩如下表:
分数 50 60 70 80 90 100
人数 甲组 2 5 10 13 14 6
乙组 4 4 16 2 12 12
已经算得两个组的平均分都是80分,请根据你所学过的统计知识,进一步判断这两个组这次竞赛中成绩谁优谁次,并说明理由.
21.某厂研制了一种生产高精产品的设备,为检验新设备生成产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 8.8 9.3 9.0 9.2 8.9 8.8 9.0 9.1 9.2 8.7
新设备 9.1 9.4 9.1 9.0 9.1 9.3 9.6 9.5 9.4 9.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生成产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高)
22.某校根据该校高一年级100名学生的英语成绩(不包括听力部分)得到如下频数分布表:
分组
频数 8 24 36 28 4
(1)根据频数分布表,作出这些数据的频率分布直方图,并求这100名学生英语成绩(不包括听力部分)的平均分(同一组中的数据用该组区间的中间值作代表);
(2)若这100名学生英语成绩的优秀率为,求英语成绩为优秀的分数线(保留整数位).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
给定的折线图,理出两校学生测试分数,再逐一分析各个选项即可判断作答.
【详解】
由图知,校学生测试分数从小到大依次为:50,51,60,63,65,69,74,76,76,78,
校学生测试分数从小到大依次为:53,55,56,61,63,64,65,65,67,73,
校学生分数的平均分,
校学生分数的平均分,A正确;
校学生分数的众数为76,校学生分数的众数为65,B正确;
校学生分数的中位数为67,校学生分数的中位数为63.5,C错误;
校学生分数分布较为分散,相对于波动较大,校学生分数分布较为集中,相对于波动较小,
即校学生分数的方差大于校学生分数的方差,D正确.
故选:C
2.D
A.增长速度都是正值,工业增加值都在增加
B.可看到,最高点是在四月
C. 2020年10月工业增加值同比增长
【详解】
由题意可知该折线统计图是工业增加值同比增长率,2020年3月份到10月份,工业增加值同比都在增加,故A错误;
2020年3月份到10月份,工业增加值同比增加速度最大的是4月,增速为,故B错误;
2020年10月工业增加值同比增长,故C错误,D正确.
故选:D
3.D
B样本数据是样本数据都减2后所得的,则A、B两样本数据的平均数、众数、中位数都发生改变,由方差的统计学意义可知, A、B的方差不变.
【详解】
由数据A : 17,22,37,42,31,58,61得到数据B: 15,20,35,40,29,56,59,
所以B的平均数、众数、中位数比A的平均数、众数、中位数均小2;
因为A、B的离散程度相同, 所以A、B的方差相同.
故选:D
(1) 平均数:是指在一组数据中所有数据之和再除以这组数据的个数,表示一组数据集中趋势的量数;
(2) 方差:是各个数据分别与其平均数之差的平方的和的平均数,数据和其数学期望(即均值)之间的偏离程度,反映数据离散程度.两组数据的离散程度相同, 所以他们的方差相同.
4.C
根据茎叶图按顺序排列第一场、第二场得分分数,中间两数的平均数即为中位数,出现次数最多的数为众数,最大数减最小数为极差,求出相应数据即可判断各项正误.
【详解】
由茎叶图可知第一场得分为:0,0,0,0,0,2,3,7,10,12,17,19,中位数为,众数为0,极差为19,第二场得分为:0,0,0,0,3,6,7,7,9,10,10,24,众数为0,平均数为,极差为24,所以选项C的说法是错误的.
故选:C
本题考查茎叶图,根据茎叶图计算样本数据的中位数、众数及平均数,属于基础题.
5.C
将数据按从小到大顺序排列,结合百分位数概念计算即可.
【详解】
将数据从小到大排列:
2710 2755 2850 2880 2880 2890
2920 2940 2950 3050 3130 3325
,故表中所给的数据计算得第85百分位数为第11位数:3130.
故选:C
6.B
由题设得或,分别求出数据变化前后的平均数、众数、中位数、标准差,再确定对应值是否发生变化.
【详解】
由题意,,可得,又中位数为4,则或,
当时,众数为5,标准差为;当时,众数为4,标准差为;
∴去掉其中的一个最大数后,数据为1,2,,,5,
当,平均数,众数为5,中位数为3,标准差为;
当时,平均数,众数为4,中位数为4,标准差为;
综上,数据变化前后一定不変的是众数.
故选:B
7.B
根据频率分布直方图可得在中的频率,进而可得.
【详解】
由图可得在中的频率为,
所以,
故选:B.
8.C
根据频率分布直方图计算直径不小于的零件所占的频率,乘以即可得出结果.
【详解】
由频率分布直方图可知,直径不小于的零件所占的频率为,
因此,在被抽取的零件中,直径不小于的个数为.
故选:C.
9.C
人口数由柱状图判断,增幅由折线图判断.
【详解】
A.人口数逐次增加,第三次增幅最大,故错误;
B.第六次普查人数最多,第六次增幅最小,故错误;
C.第六次普查人数最多,第三次增幅最大,故正确;
D.人口数逐次增加,从第三次开始增幅减小,故错误;
故选:C
10.C
根据均值和方差的公式计算可结果.
【详解】
设一组数据为,平均数为,方差为,所得一组新数据为,平均数为,方差为,
则,,
所以,
所以,所以,
由题意得,
所以,
所以
所以,
所以,所以.
故选:C.
关键点点睛:熟练掌握几个数据的均值和方差公式是解题关键.
11.B
根据频率分布直方图读出众数a,计算中位数b,平均数c,再比较大小.
【详解】
由频率分布直方图可知:众数;
中位数应落在70-80区间内,则有:,解得:;
平均数
=4.5+8.25+9.75+22.5+21.25+4.75=71
所以
故选:B
从频率分布直方图可以估计出的几个数据:
(1)众数:频率分布直方图中最高矩形的底边中点的横坐标;
(2)平均数:频率分布直方图每组数值的中间值乘以频率后相加;
(3)中位数:把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标.
12.C
根据拆线图的性质逐一判断即可.
【详解】
对于①,由折线图知这11天的复工复产指数有增有减,故①错.
对于②,由第1天和第11天复工和复产指数位置可知,复产指数的增量小于复工指数的增量,故②错.
对于③,由折线图知,第3天至第11天复工、复产指数均超过80%,故③正确.
对于④,由折线图知,第9天至第11天复产指数增量大于复工指数的增量,故④正确.
故选:C
13.A
根据条形图计算出刚退休时就医费用,进而计算出现在的就医费用,结合目前就医费用所占退休金的比例可得出结果.
【详解】
刚退休时就医费用为元,现在的就医费用为元,占退休金的,
因此,目前该教师的月退休金为元.
故选:A
14.A
根据频率分布直方图,及年龄在内的有1400人,可知总人数,进而确定答案.
【详解】
假设总人数为,则,解得,
∴,解得,
故选:A.
15.C
根据,,的平均和方差是得出,
求出,,,11这4个数据得方差为即可得出答案.
【详解】
解:由已知得,,
则新数据的平均数为,
所以方差为
,
故选:C
16.平均数
根据定义分别计算甲、乙两组数据平均数,中位数,极差,由此确定答案.
【详解】
甲组数据的平均数为,极差为32,中位数为18.5,
乙组数据的平均数为,极差为38,中位数为16,
所以甲、乙两组数据的平均数相同,
故答案为:平均数.
17.0.52
根据换算方法,及格率与实际及格率的差是内的频率求解.
【详解】
由频率分布直方图,得卷面得分在内的频率为:,
所以按照这种方式求出的及格率与实际及格率的差是0.52.
故答案为:0.52
18.
根据方差公式与平均值公式即可求解.
【详解】
设每天生产平均值为
依题意得
所以
又因为 ,
所以解得
故答案为:
19.(1)图见解析
(2)答案见解析
(1)直接按照茎叶图定义画出即可;
(2)通过中位数、平均数、方差依次比较.
(1)
甲、乙两人数学成绩的茎叶图如图所示:
(2)
①从整体分析:乙同学的得分情况是大致对称的,中位数是;甲同学的得分情况,也大致对称,中位数是;
②平均分的角度分析:甲同学的平均分为,
乙同学的平均分为,乙同学的平均成绩比甲同学高;
③方差(稳定性)的角度:乙同学的成绩比较稳定,总体情况比甲同学好.
20.见解析
【详解】
试题分析:根据题目所提供的甲组和乙组的竞赛成绩,用我们所学过的统计知识进行分析对比判断两组这次竞赛成绩,首先平均分一致,平均实力相当,其一看众数甲组好于乙组,其二看方差甲组较小,说明甲组成绩较稳定,其三看中位数甲组在中位数以上的人数比乙组在中位数以上的人数多,说明甲组总体成绩较好,其四高分段人数和满分人数乙组人数较多,乙组好于甲组,从不同角度利用统计量数据的考查可以得出相应的判断.
试题解析:
(1)甲组成绩的众数为90分,乙组成绩的众数为70分,从成绩的众数比较看,甲组成绩好些.
(2)×[2×(50-80)2+5×(60-80)2+10×(70-80)2+13×(80-80)2+14×(90-80)2+6×(100-80)2]=×(2×900+5×400+10×100+13×0+14×100+6×400)=172.
=×(4×900+4×400+16×100+2×0+12×100+12×400)=256.
因为,所以甲组成绩较乙组成绩稳定.
(3)甲、乙两组成绩的中位数、平均数都是80分,其中甲组成绩在80分以上(含80分)的有33人,乙组成绩在80分以上(含80分)的有26人,从这一角度看,甲组成绩总体较好.
(4)从成绩统计表看,甲组成绩大于或等于90分的人数为20人,乙组成绩大于或等于90分的人数为24人,所以乙组成绩在高分阶段的人数多,同时,乙组得满分的比甲组得满分的多6人,从这一角度看,乙组成绩较好.
利用统计数据,借助我们所学过的统计量进行计算分析对比,判断两组竞赛成绩谁优谁欠,第一计算平均分,平均反映出两组实力的强弱,当平均分一致时,计算方差,当方差较小时,说明成绩较稳定,另外看众数较大的组成绩较好,还有中位数,两组在中位数以上的人数哪个组人数较多,说明那个组总体成绩较好,最后高分段人数和满分人数哪个组人数较多,说明那个组好,因此要从不同角度利用统计量数据的考查可以得出相应的判断.
21.(1),,,;
(2)新设备生产产品的该项指标的均值较旧设备有显著提高.
(1)根据平均数和方差的计算方法,计算出平均数和方差.
(2)根据题目所给判断依据,结合(1)的结论进行判断.
【详解】
(1),
,
由得
,
.
(2)依题意,,,得,
所以新设备生产产品的该项指标的均值较旧设备有显著提高.
22.(1)频率分布直方图答案见解析,平均分;(2)分数线为99.
(1)作出频率分布直方图,结合频率分布直方图的性质能求出平均分.(2)由题可知,,的频率为0.04,,的频率为0.28,由此能求出英语成绩为优秀的分数线.
【详解】
解:(1)频率分布直方图如下:
平均分.
(2)由题可知,的频率为0.04,
的频率为0.28,
因为这100名学生英语成绩的优秀率为,所以成绩优秀的分数线在之间,
设优秀成绩的分数线为x,则有.1
解得.
故英语成绩为优秀的分数线为99.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.为了增强大学生的环保意识,加强对“碳中和”概念的宣传,某公益组织分别在两所大学随机选取10名学生进行环保问题测试(满分100分),这20名学生得分的折线图如图所示,关于这两所学校被选取的学生的得分,下列结论错误的是( )
A.校学生分数的平均分大于校学生分数的平均分
B.校学生分数的众数大于校学生分数的众数
C.校学生分数的中位数等于校学生分数的中位数
D.校学生分数的方差大于校学生分数的方
2.安徽省统计局2020年11月20日发布了全省规模以上工业增加值同比增长速度(注:增加值增长速度均为扣除价格因素的实际增长率,同比是指在相邻时段内某一相同时间点进行比较),如下折线统计图所示,则下列说法正确的是( )
A.2020年3月份到10月份,工业增加值同比有增加也有下降
B.2020年3月份到10月份,工业增加值同比增加速度最大的是8月
C.2020年10月工业增加值同比下降
D.2020年10月工业增加值同比增长
3.在某次测量中得到的样本数据如下17,22,37,42,31,58,61,若B样本数据恰好是样本数据都减2后所得数据,则,两样本的下列数字特征对应相同的是( )
A.平均数 B.众数 C.中位数 D.方差
4.第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法错误的是( )
A.第一场得分的中位数为 B.第二场得分的平均数为
C.第一场得分的极差大于第二场得分的极差 D.第一场与第二场得分的众数相等
5.下表为12名毕业生的起始月薪:
毕业生 起始月薪 毕业生 起始月薪
1 2850 7 2890
2 2950 8 3130
3 3050 9 2940
4 2880 10 3325
5 2755 11 2920
6 2710 12 2880
根据表中所给的数据计算第85百分位数为( )A.2710 B.2890 C.3130 D.2940
6.已知一组数据1,2,,,5,8的平均数和中位数均为4,其中,在去掉其中的一个最大数后,该组数据一定不变的是( )
A.平均数 B.众数 C.中位数 D.标准差
7.为了解学生课外阅读的情况,随机统计了名学生的课外阅读时间,所得数据都在中,其频率分布直方图如图所示.已知在中的频数为100,则的值是( )
A.500 B.1000 C.10000 D.25000
8.从一批零件中抽取个,测量其直径(单位:),将所得数据分为组:、、、、,并整理得到频率分布直方图,则在被抽取的零件中,直径不小于的个数为( )
A. B. C. D.
9.人口普查是世界各国所广泛采用的搜集人口资料的一种科学方法,是提供全国基本人口数据的主要来源.根据人口普查的基本情况,可以科学的研究制定社会、经济、科教等各项发展政策,是国家科学决策的重要基础工作,人口普查资料是制定人口政策的依据和前提.截止2020年10月10日,我国共进行了六次人口普查,下图是这六次人口普查的人数和增幅情况,下列说法正确的是( )
A.人口数逐次增加,第二次增幅最大 B.第六次普查人数最多,第四次增幅最小
C.第六次普查人数最多,第三次增幅最大 D.人口数逐次增加,从第二次开始增幅减小
10.一组数据中的每一个数据都乘以3,再减去50,得到一组新数据,若求得新的数据的平均数是1.6,方差是3.6,则原来数据的平均数和方差分别是( )
A.17.2,3.6 B.54.8,3.6 C.17.2,0.4 D.54.8,0.4
11.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
12.我国新冠肺炎疫情防控进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
①这11天复工指数和复产指数均逐日增加;
②这11天期间,复产指数增量大于复工指数的增量;
③第3天至第11天复工复产指数均超过80%;
④第9天至第11天复产指数增量大于复工指数的增量.
A.①③④ B.②③④
C.③④ D.①④
13.若干年前,某老师刚退休的月退休金为4000元,月退休金各种用途占比统计图如下面的条形图.该老师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该老师的月退休金为( )
A.5000元 B.5500元 C.6000元 D.6500元
14.为检测疫苗的有效程度,某权威部门对某种疫苗进行的三期临床效果比较明显的受试者,按照年龄进行分组,绘制了如图所示的样本频率分布直方图,其中年龄在内的有1400人,在内有800人,则频率分布直方图中的值为( )
A.0.008 B.0.08 C.0.006 D.0.06
15.已知一组数据,,的平均数是5,方差是4则由,,,11这4个数据组成的新的一组数据的方差是( )
A.16 B.14 C.12 D.8
二、填空题
16.甲组数据为,乙组数据为,则甲、乙两组数据的平均数、极差及中位数相同的是_________
17.某测试卷的满分为100分,60分及以上为及格.现有100人参加测试,将这100人的卷面分数按照,,,分组后绘制的频率分布直方图如图所示.由于及格人数较少,某位老师准备将每位学生的卷面得分采用“开方乘以10取整”的方法进行换算以提高及格率(实数a的取整为不超过a的最大整数),如:某位学生卷面得分为49分,则换算成70分作为最终考试成绩,则按照这种方法求出的及格率与实际及格率的差是______.
18.A工厂年前加紧手套生产,设该工厂连续5天生产的手套数依次为x1,x2,x3,x4,x5(单位:万只),若这组数据x1,x2,x3,x4,x5的方差为1.44,且x12,x22,x32,x42,x52的平均数为4,则该工厂这5天平均每天生产手套___________万只.
三、解答题
19.现有银川二中高一年级某班甲、乙两名学生自进入高中以来的历次数学成绩(单位:分),具体考试成绩如下:
甲:、、、、、、、、、、、、;
乙:、、、、、、、、、、、、.
(1)请你画出两人数学成绩的茎叶图;
(2)根据茎叶图,运用统计知识对两人的成绩进行比较.(最少写出两条统计结论)
20.一次数学知识竞赛中,两组学生成绩如下表:
分数 50 60 70 80 90 100
人数 甲组 2 5 10 13 14 6
乙组 4 4 16 2 12 12
已经算得两个组的平均分都是80分,请根据你所学过的统计知识,进一步判断这两个组这次竞赛中成绩谁优谁次,并说明理由.
21.某厂研制了一种生产高精产品的设备,为检验新设备生成产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 8.8 9.3 9.0 9.2 8.9 8.8 9.0 9.1 9.2 8.7
新设备 9.1 9.4 9.1 9.0 9.1 9.3 9.6 9.5 9.4 9.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生成产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高)
22.某校根据该校高一年级100名学生的英语成绩(不包括听力部分)得到如下频数分布表:
分组
频数 8 24 36 28 4
(1)根据频数分布表,作出这些数据的频率分布直方图,并求这100名学生英语成绩(不包括听力部分)的平均分(同一组中的数据用该组区间的中间值作代表);
(2)若这100名学生英语成绩的优秀率为,求英语成绩为优秀的分数线(保留整数位).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
给定的折线图,理出两校学生测试分数,再逐一分析各个选项即可判断作答.
【详解】
由图知,校学生测试分数从小到大依次为:50,51,60,63,65,69,74,76,76,78,
校学生测试分数从小到大依次为:53,55,56,61,63,64,65,65,67,73,
校学生分数的平均分,
校学生分数的平均分,A正确;
校学生分数的众数为76,校学生分数的众数为65,B正确;
校学生分数的中位数为67,校学生分数的中位数为63.5,C错误;
校学生分数分布较为分散,相对于波动较大,校学生分数分布较为集中,相对于波动较小,
即校学生分数的方差大于校学生分数的方差,D正确.
故选:C
2.D
A.增长速度都是正值,工业增加值都在增加
B.可看到,最高点是在四月
C. 2020年10月工业增加值同比增长
【详解】
由题意可知该折线统计图是工业增加值同比增长率,2020年3月份到10月份,工业增加值同比都在增加,故A错误;
2020年3月份到10月份,工业增加值同比增加速度最大的是4月,增速为,故B错误;
2020年10月工业增加值同比增长,故C错误,D正确.
故选:D
3.D
B样本数据是样本数据都减2后所得的,则A、B两样本数据的平均数、众数、中位数都发生改变,由方差的统计学意义可知, A、B的方差不变.
【详解】
由数据A : 17,22,37,42,31,58,61得到数据B: 15,20,35,40,29,56,59,
所以B的平均数、众数、中位数比A的平均数、众数、中位数均小2;
因为A、B的离散程度相同, 所以A、B的方差相同.
故选:D
(1) 平均数:是指在一组数据中所有数据之和再除以这组数据的个数,表示一组数据集中趋势的量数;
(2) 方差:是各个数据分别与其平均数之差的平方的和的平均数,数据和其数学期望(即均值)之间的偏离程度,反映数据离散程度.两组数据的离散程度相同, 所以他们的方差相同.
4.C
根据茎叶图按顺序排列第一场、第二场得分分数,中间两数的平均数即为中位数,出现次数最多的数为众数,最大数减最小数为极差,求出相应数据即可判断各项正误.
【详解】
由茎叶图可知第一场得分为:0,0,0,0,0,2,3,7,10,12,17,19,中位数为,众数为0,极差为19,第二场得分为:0,0,0,0,3,6,7,7,9,10,10,24,众数为0,平均数为,极差为24,所以选项C的说法是错误的.
故选:C
本题考查茎叶图,根据茎叶图计算样本数据的中位数、众数及平均数,属于基础题.
5.C
将数据按从小到大顺序排列,结合百分位数概念计算即可.
【详解】
将数据从小到大排列:
2710 2755 2850 2880 2880 2890
2920 2940 2950 3050 3130 3325
,故表中所给的数据计算得第85百分位数为第11位数:3130.
故选:C
6.B
由题设得或,分别求出数据变化前后的平均数、众数、中位数、标准差,再确定对应值是否发生变化.
【详解】
由题意,,可得,又中位数为4,则或,
当时,众数为5,标准差为;当时,众数为4,标准差为;
∴去掉其中的一个最大数后,数据为1,2,,,5,
当,平均数,众数为5,中位数为3,标准差为;
当时,平均数,众数为4,中位数为4,标准差为;
综上,数据变化前后一定不変的是众数.
故选:B
7.B
根据频率分布直方图可得在中的频率,进而可得.
【详解】
由图可得在中的频率为,
所以,
故选:B.
8.C
根据频率分布直方图计算直径不小于的零件所占的频率,乘以即可得出结果.
【详解】
由频率分布直方图可知,直径不小于的零件所占的频率为,
因此,在被抽取的零件中,直径不小于的个数为.
故选:C.
9.C
人口数由柱状图判断,增幅由折线图判断.
【详解】
A.人口数逐次增加,第三次增幅最大,故错误;
B.第六次普查人数最多,第六次增幅最小,故错误;
C.第六次普查人数最多,第三次增幅最大,故正确;
D.人口数逐次增加,从第三次开始增幅减小,故错误;
故选:C
10.C
根据均值和方差的公式计算可结果.
【详解】
设一组数据为,平均数为,方差为,所得一组新数据为,平均数为,方差为,
则,,
所以,
所以,所以,
由题意得,
所以,
所以
所以,
所以,所以.
故选:C.
关键点点睛:熟练掌握几个数据的均值和方差公式是解题关键.
11.B
根据频率分布直方图读出众数a,计算中位数b,平均数c,再比较大小.
【详解】
由频率分布直方图可知:众数;
中位数应落在70-80区间内,则有:,解得:;
平均数
=4.5+8.25+9.75+22.5+21.25+4.75=71
所以
故选:B
从频率分布直方图可以估计出的几个数据:
(1)众数:频率分布直方图中最高矩形的底边中点的横坐标;
(2)平均数:频率分布直方图每组数值的中间值乘以频率后相加;
(3)中位数:把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标.
12.C
根据拆线图的性质逐一判断即可.
【详解】
对于①,由折线图知这11天的复工复产指数有增有减,故①错.
对于②,由第1天和第11天复工和复产指数位置可知,复产指数的增量小于复工指数的增量,故②错.
对于③,由折线图知,第3天至第11天复工、复产指数均超过80%,故③正确.
对于④,由折线图知,第9天至第11天复产指数增量大于复工指数的增量,故④正确.
故选:C
13.A
根据条形图计算出刚退休时就医费用,进而计算出现在的就医费用,结合目前就医费用所占退休金的比例可得出结果.
【详解】
刚退休时就医费用为元,现在的就医费用为元,占退休金的,
因此,目前该教师的月退休金为元.
故选:A
14.A
根据频率分布直方图,及年龄在内的有1400人,可知总人数,进而确定答案.
【详解】
假设总人数为,则,解得,
∴,解得,
故选:A.
15.C
根据,,的平均和方差是得出,
求出,,,11这4个数据得方差为即可得出答案.
【详解】
解:由已知得,,
则新数据的平均数为,
所以方差为
,
故选:C
16.平均数
根据定义分别计算甲、乙两组数据平均数,中位数,极差,由此确定答案.
【详解】
甲组数据的平均数为,极差为32,中位数为18.5,
乙组数据的平均数为,极差为38,中位数为16,
所以甲、乙两组数据的平均数相同,
故答案为:平均数.
17.0.52
根据换算方法,及格率与实际及格率的差是内的频率求解.
【详解】
由频率分布直方图,得卷面得分在内的频率为:,
所以按照这种方式求出的及格率与实际及格率的差是0.52.
故答案为:0.52
18.
根据方差公式与平均值公式即可求解.
【详解】
设每天生产平均值为
依题意得
所以
又因为 ,
所以解得
故答案为:
19.(1)图见解析
(2)答案见解析
(1)直接按照茎叶图定义画出即可;
(2)通过中位数、平均数、方差依次比较.
(1)
甲、乙两人数学成绩的茎叶图如图所示:
(2)
①从整体分析:乙同学的得分情况是大致对称的,中位数是;甲同学的得分情况,也大致对称,中位数是;
②平均分的角度分析:甲同学的平均分为,
乙同学的平均分为,乙同学的平均成绩比甲同学高;
③方差(稳定性)的角度:乙同学的成绩比较稳定,总体情况比甲同学好.
20.见解析
【详解】
试题分析:根据题目所提供的甲组和乙组的竞赛成绩,用我们所学过的统计知识进行分析对比判断两组这次竞赛成绩,首先平均分一致,平均实力相当,其一看众数甲组好于乙组,其二看方差甲组较小,说明甲组成绩较稳定,其三看中位数甲组在中位数以上的人数比乙组在中位数以上的人数多,说明甲组总体成绩较好,其四高分段人数和满分人数乙组人数较多,乙组好于甲组,从不同角度利用统计量数据的考查可以得出相应的判断.
试题解析:
(1)甲组成绩的众数为90分,乙组成绩的众数为70分,从成绩的众数比较看,甲组成绩好些.
(2)×[2×(50-80)2+5×(60-80)2+10×(70-80)2+13×(80-80)2+14×(90-80)2+6×(100-80)2]=×(2×900+5×400+10×100+13×0+14×100+6×400)=172.
=×(4×900+4×400+16×100+2×0+12×100+12×400)=256.
因为,所以甲组成绩较乙组成绩稳定.
(3)甲、乙两组成绩的中位数、平均数都是80分,其中甲组成绩在80分以上(含80分)的有33人,乙组成绩在80分以上(含80分)的有26人,从这一角度看,甲组成绩总体较好.
(4)从成绩统计表看,甲组成绩大于或等于90分的人数为20人,乙组成绩大于或等于90分的人数为24人,所以乙组成绩在高分阶段的人数多,同时,乙组得满分的比甲组得满分的多6人,从这一角度看,乙组成绩较好.
利用统计数据,借助我们所学过的统计量进行计算分析对比,判断两组竞赛成绩谁优谁欠,第一计算平均分,平均反映出两组实力的强弱,当平均分一致时,计算方差,当方差较小时,说明成绩较稳定,另外看众数较大的组成绩较好,还有中位数,两组在中位数以上的人数哪个组人数较多,说明那个组总体成绩较好,最后高分段人数和满分人数哪个组人数较多,说明那个组好,因此要从不同角度利用统计量数据的考查可以得出相应的判断.
21.(1),,,;
(2)新设备生产产品的该项指标的均值较旧设备有显著提高.
(1)根据平均数和方差的计算方法,计算出平均数和方差.
(2)根据题目所给判断依据,结合(1)的结论进行判断.
【详解】
(1),
,
由得
,
.
(2)依题意,,,得,
所以新设备生产产品的该项指标的均值较旧设备有显著提高.
22.(1)频率分布直方图答案见解析,平均分;(2)分数线为99.
(1)作出频率分布直方图,结合频率分布直方图的性质能求出平均分.(2)由题可知,,的频率为0.04,,的频率为0.28,由此能求出英语成绩为优秀的分数线.
【详解】
解:(1)频率分布直方图如下:
平均分.
(2)由题可知,的频率为0.04,
的频率为0.28,
因为这100名学生英语成绩的优秀率为,所以成绩优秀的分数线在之间,
设优秀成绩的分数线为x,则有.1
解得.
故英语成绩为优秀的分数线为99.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
