必修第二册第九章统计 单元练习(Word版含解析)
文档属性
| 名称 | 必修第二册第九章统计 单元练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 888.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览



文档简介
人教A版(2019)必修第二册 第九章 统计 同步练习
一、单选题
1.在高一(1)班组织的“我爱古诗词”的调研考试中,全班40名学生的成绩数据(均为整数且都在)统计为如下的频率分布直方图,则第四小组(成绩分布在)的频率为( )
A.0.001 B.0.01 C.0.03 D.0.3
2.10名工人某天生产同一零件,生产的件数是15、17、14、10、15、17、17、16、14、12.设其平均数为a,中位数为b,众数为c,则有( )
A. B. C. D.
3.已知甲 乙两组数据(已按从小到大的顺序排列):甲组:27,28,39,40,m,50;乙组:24,n,34,43,48,52.若这两组数据的30百分位数 80百分位数分别相等,则等于( )
A. B. C. D.
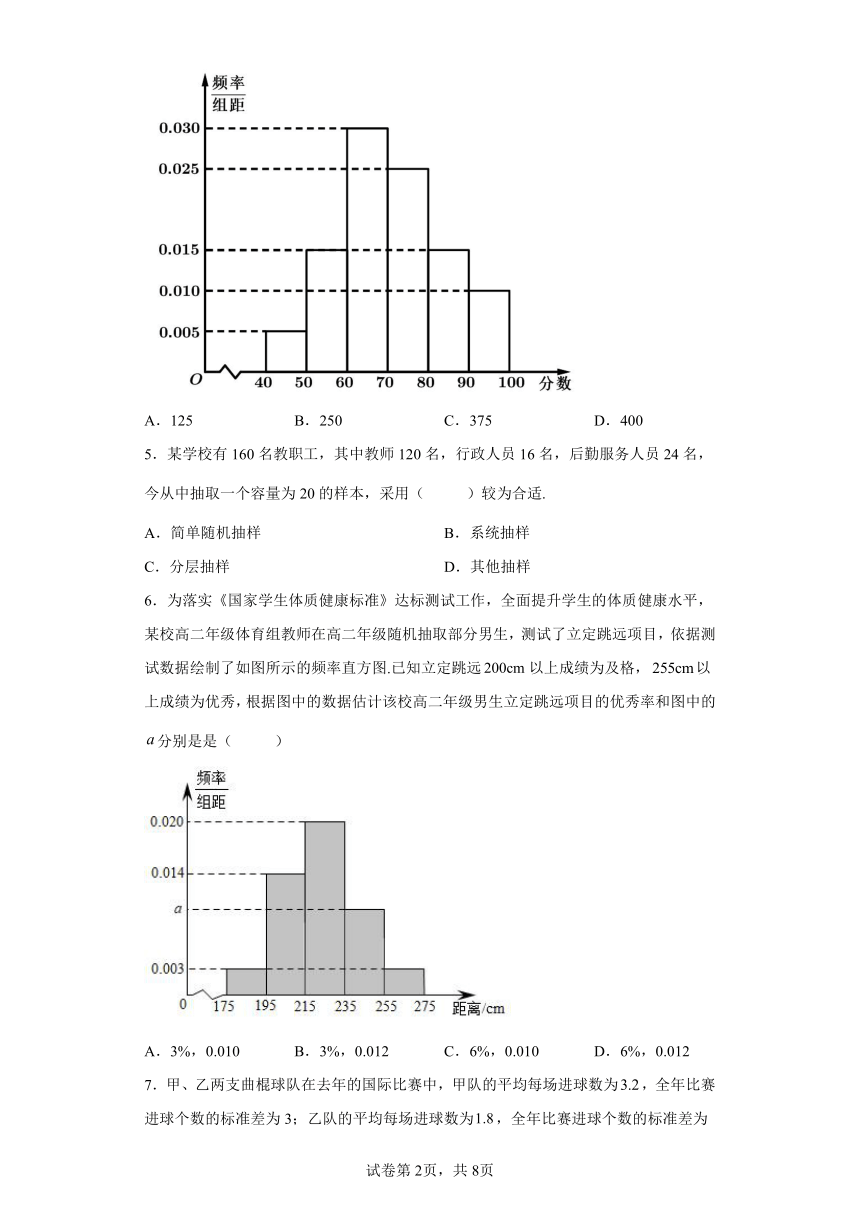
4.2020年是脱贫攻坚战决胜之年凝心聚力打赢脫贫攻坚战,确保全面建成小康社会某县举行扶贫知识政策答题比赛,分初赛和复赛两个阶段进行规定:初赛成绩大于80分的进入复赛,某校有500名学生参加了初赛,所有学生的成绩均在区间内,其频率分布直方图如图所示,则进入复赛的人数为( )
A.125 B.250 C.375 D.400
5.某学校有160名教职工,其中教师120名,行政人员16名,后勤服务人员24名,今从中抽取一个容量为20的样本,采用( )较为合适.
A.简单随机抽样 B.系统抽样
C.分层抽样 D.其他抽样
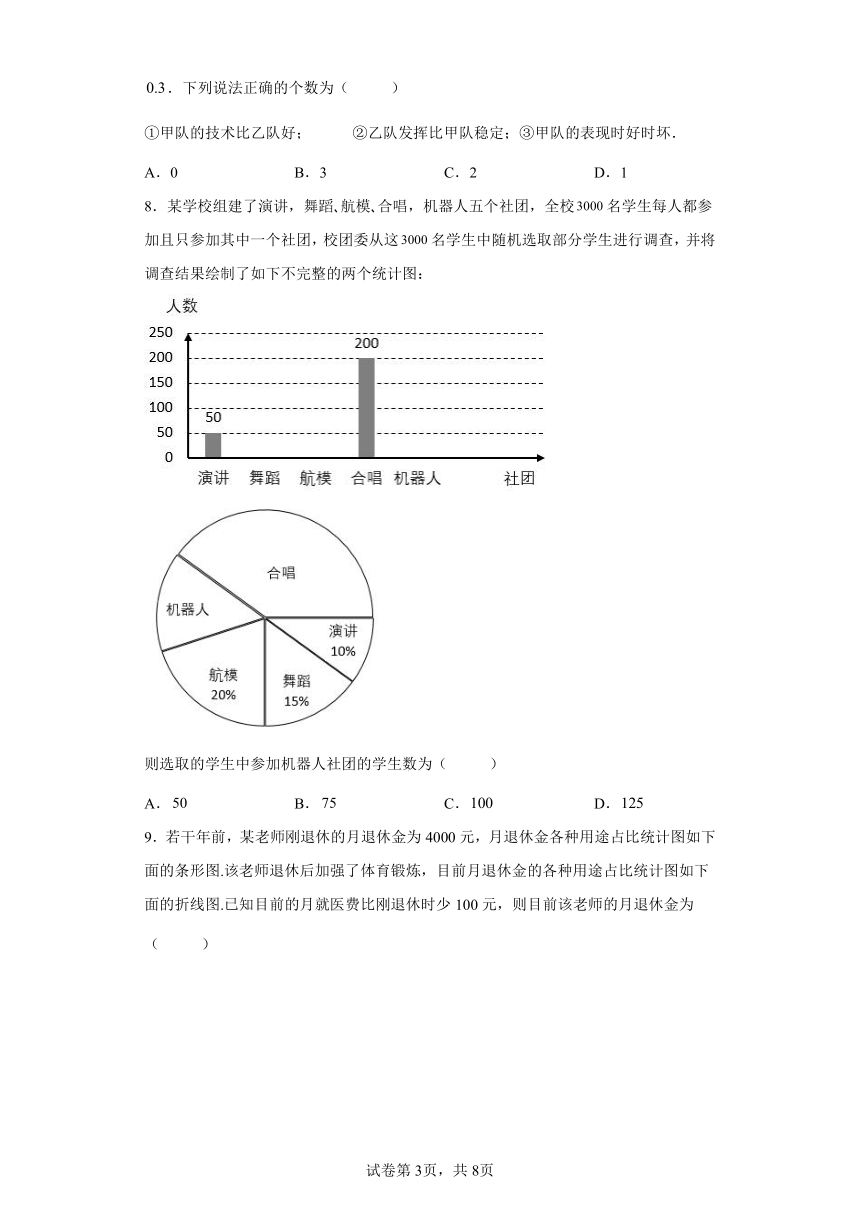
6.为落实《国家学生体质健康标准》达标测试工作,全面提升学生的体质健康水平,某校高二年级体育组教师在高二年级随机抽取部分男生,测试了立定跳远项目,依据测试数据绘制了如图所示的频率直方图.已知立定跳远以上成绩为及格,以上成绩为优秀,根据图中的数据估计该校高二年级男生立定跳远项目的优秀率和图中的分别是是( )
A.3%,0.010 B.3%,0.012 C.6%,0.010 D.6%,0.012
7.甲、乙两支曲棍球队在去年的国际比赛中,甲队的平均每场进球数为,全年比赛进球个数的标准差为3;乙队的平均每场进球数为,全年比赛进球个数的标准差为.下列说法正确的个数为( )
①甲队的技术比乙队好; ②乙队发挥比甲队稳定;③甲队的表现时好时坏.
A.0 B.3 C.2 D.1
8.某学校组建了演讲,舞蹈 航模 合唱,机器人五个社团,全校名学生每人都参加且只参加其中一个社团,校团委从这名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为( )
A. B. C. D.
9.若干年前,某老师刚退休的月退休金为4000元,月退休金各种用途占比统计图如下面的条形图.该老师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该老师的月退休金为( )
A.5000元 B.5500元 C.6000元 D.6500元
10.我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,大数据的相关岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
数据开发 8% 25% 32% 35%
数据分析 15% 36% 32% 17%
数据挖掘 9% 12% 28% 51%
数据产品 7% 17% 41% 35%
由表中数据可得该市大数据相关的各类岗位的薪资水平高低情况为( )A.数据挖掘>数据开发>数据产品>数据分析 B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品 D.数据挖掘>数据产品>数据分析>数据开发
11.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
12.已知某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的平均数为,方差为,则( )
A., B.,
C., D.,
二、填空题
13.现凯里一中高一年级、高二年级、高三年级的学生人数分别是1500、2000、2500人,现用分层抽样方法在全校抽取一个容量为120人的样本,则高二年级应该抽_______人.
14.下列数据是30个不同国家中每100000名男性患某种疾病的死亡率:
27.0 23.9 41.6 33.1 40.6 18.8 13.7 28.9 13.2 14.5
27.0 34.8 28.9 3.2 50.1 5.6 8.7 15.2 7.1 5.2
16.5 13.8 19.2 11.2 15.7 10.0 5.6 1.5 33.8 9.2
这组数据的第40百分位数是________.
15.在用抽签法抽样时,有下列五个步骤:
(1)从箱中每次抽出1个号签,并记录其编号,连续抽取k次;
(2)将总体中的所有个体编号;
(3)制作号签;
(4)将总体中与抽到的签的编号相一致的个体取出构成样本;
(5)将号签放在同一箱中,并搅拌均匀.
以上步骤的次序是______________.
16.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为___________.
三、解答题
17.现有银川二中高一年级某班甲、乙两名学生自进入高中以来的历次数学成绩(单位:分),具体考试成绩如下:
甲:、、、、、、、、、、、、;
乙:、、、、、、、、、、、、.
(1)请你画出两人数学成绩的茎叶图;
(2)根据茎叶图,运用统计知识对两人的成绩进行比较.(最少写出两条统计结论)
18.治理沙漠离不开优质的树苗,现从苗圃中随机地抽测了200株树苗的高度(单位:cm),得到以下频率分布直方图.
(1)求直方图中a的值及众数 中位数;
(2)若树高185cm及以上是可以移栽的合格树苗.从样本中按分层抽样方法抽取20株树苗作进一步研究,不合格树苗 合格树苗分别应抽取多少株?
19.某校有高中生2000人,其中男女生比例约为,为了获得该校全体高中生的身高信息,采取了以下两种方案:方案一:采用比例分配的分层随机抽样方法,抽收了样本容量为的样本,得到频数分布表和频率分布直方图.方案二:采用分层随机抽样方法,抽取了男、女生样本量均为25的样本,计算得到男生样本的均值为170,方差为16,女生样本的均值为160,方差为20.
身高(单位:)
频数 6 4
(1)根据图表信息,求,并补充完整频率分布直方图,估计该校高中生的身高均值;(同一组中的数据以这组数据所在区间中点的值为代表)
(2)计算方案二中总样本的均值及方差;
(3)计算两种方案总样本均值的差,并说明用方案二总样本的均值作为总体均值的估计合适吗?为什么?
20.从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到频数分布表和频率分布直方图如下.
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18) 2
合计 100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率分布直方图中的a,b的值.
21.某校根据该校高一年级100名学生的英语成绩(不包括听力部分)得到如下频数分布表:
分组
频数 8 24 36 28 4
(1)根据频数分布表,作出这些数据的频率分布直方图,并求这100名学生英语成绩(不包括听力部分)的平均分(同一组中的数据用该组区间的中间值作代表);
(2)若这100名学生英语成绩的优秀率为,求英语成绩为优秀的分数线(保留整数位).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
根据频率之和为1可求出.
【详解】
由频率分布直方图可得第四小组的频率为.
故选:D.
2.B
将样本数据由小到大进行排列,根据定义求出,即可得出结论.
【详解】
解:将生产的件数由小到大排列为:10、12、14、14、15、15、16、17、17、17,
∴ ,中位数为,
众数为,
因此,,
故选:B.
3.A
根据百分位数的定义并结合已知条件求出的值,由此可得的值.
【详解】
因为×6=1.8,×6=4.8,所以30百分位数为第二个数,即n=28,80百分位数为第五个数即m=48,所以==.
故选:A
4.A
根据直方图求得成绩大于80分的频率,然后乘以总人数即得所求.
【详解】
由直方图可知,成绩大于80分的频率为,
又∵总人数为500人,所以进入复赛的人数为500×0.25=125,
故选:A.
本题考查直方图,关键是理解直方图的意义.
5.C
利用分层抽样的概念求解.
【详解】
由题知,学校教职工有3种类别,所以选用分层抽样较为合适.
故选:C.
6.C
根据频率分布直方图可直接求出优秀率,根据频率之和为,可求出.
【详解】
由频率分布直方图可得,优秀率为;
由,解得;
故选:C.
7.B
根据平均数、方差的知识,对四个说法逐一分析,由此得出正确选项.
【详解】
∵甲队平均数大于乙队的平均数,∴甲队的技术比乙队好,
又∵甲队的标准差大于乙队的标准差,∴乙队发挥比甲队稳定,甲队的表现时好时坏,故①②③都对.
故选:B
本题主要考查平均数、方差在实际生活中的应用,属于基础题.
8.B
根据演讲的人数,求得本次调查的人数为人,进而求得机器人所占的比例,即可求解.
【详解】
由题意,本次调查的人数为人,
其中合唱比赛所占的比例为,
所以机器人所占的比例为,
所以选取的学生中参加机器人社团的学生数为人.
故选:B.
9.A
根据条形图计算出刚退休时就医费用,进而计算出现在的就医费用,结合目前就医费用所占退休金的比例可得出结果.
【详解】
刚退休时就医费用为元,现在的就医费用为元,占退休金的,
因此,目前该教师的月退休金为元.
故选:A
10.B
根据题意和表格的数据分别计算数据开发、数据分析、数据产品的平均薪资,进而比较大小即可.
【详解】
由题中选项知数据挖掘的平均薪资最高,故只需计算并比较其他三类工作岗位的平均薪资.估计数据开发的平均薪资为;
估计数据分析的平均薪资为;
估计数据产品的平均薪资为.
故数据挖掘>数据产品>数据开发>数据分析.
故选:B.
11.A
可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】
设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
12.A
由题设条件,利用平均数和方差的计算公式计算即可求解.
【详解】
设7个数为,
则,
,
所以,
所以,
则这个数的平均数为,
方差为.
故选:A.
13.40
由样本与总体所占比例相等可得.
【详解】
设高二年级应该抽取人,则,解得.
故答案为:40.
14.13.75
将数据从小到大排列,由,所求数为第12和第13两数的平均数.
【详解】
将数据按从小到大排列为
1.5 3.2 5.2 5.6 5.6 7.1 8.7 9.2
10.0 11.2 13.2 13.7 13.8 14.5 15.2 15.7
16.5 18.8 19.2 23.9 27 27 28.9 28.9
33.1 33.8 34.8 40.6 41.6 50.1
,
这组数据的第40百分位数是.
故答案为:
本题考查求百分位数,属于基础题.
15.(2)(3)(5)(1)(4)
按照抽签法的步骤判断,即编号,做号签,放入容器,进行抽取,构成样本.
【详解】
利用抽签法第一步要进行编号,然后做号签,放入容器,接下来按照逐个不放回地抽取号签,最后将与编号一致的个体取出构成样本,故这些步骤的先后顺序为(2)(3)(5)(1)(4).
故答案为:(2)(3)(5)(1)(4).
16.0.98.
本题考查通过统计数据进行概率的估计,采取估算法,利用概率思想解题.
【详解】
由题意得,经停该高铁站的列车正点数约为,其中高铁个数为10+20+10=40,所以该站所有高铁平均正点率约为.
本题考点为概率统计,渗透了数据处理和数学运算素养.侧重统计数据的概率估算,难度不大.易忽视概率的估算值不是精确值而失误,根据分类抽样的统计数据,估算出正点列车数量与列车总数的比值.
17.(1)图见解析
(2)答案见解析
(1)直接按照茎叶图定义画出即可;
(2)通过中位数、平均数、方差依次比较.
(1)
甲、乙两人数学成绩的茎叶图如图所示:
(2)
①从整体分析:乙同学的得分情况是大致对称的,中位数是;甲同学的得分情况,也大致对称,中位数是;
②平均分的角度分析:甲同学的平均分为,
乙同学的平均分为,乙同学的平均成绩比甲同学高;
③方差(稳定性)的角度:乙同学的成绩比较稳定,总体情况比甲同学好.
18.(1),众数为,中位数
(2)7株和13株
(1)利用频率分布直方图的性质及众数 中位数的求法即得;
(2)利用直方图及分层抽样方法即得.
(1)
∵,
∴,众数为,
设中位数为x,因为,
,
则,
,
∴
故,众数为,中位数.
(2)
由题可知合格树苗所占频率为,不合格树苗所占频率为,
不合格的抽取株,合格的抽取株,
故不合格树苗 合格树苗分别应抽取7株和13株.
19.(1),,频率分布直方图见解析,身高均值(2)均值为,方差为;(3)总样本均值的差为,不合适,理由见解析.
(1)利用身高在区间的频率和频数即可求的值,进而可得的值,求出各组的频率即可补全频率分布直方图,由平均数的计算公式即可求身高均值;
(2)把男生样本记为:,其均值为,方差为,把女生样本记为:,其均值为,方差为,则总体样本均值为,
根据方差公式和平均数公式变形即可得样本总体方差.
(3)两个方案的均值相减即可求均值差,由于没有进行等比例的分层抽样,每个个体被抽到的可能性不同,代表性较差,因此不合适.
【详解】
(1)因为身高在区间的频率为,频数为,
所以样本容量为,,,
,
所以身高在的频率为,小矩形的高为,
所以身高在的频率为,小矩形的高为,
由此补全频率分布直方图:
由频率分布直方图可知:样本的身高均值为:
,
所以由样本估计总体可知,估计该校高中生的身高均值为
(2)把男生样本记为:,其均值为,方差为,
把女生样本记为:,其均值为,方差为,
总体样本均值记为,方差记为,
所以,
又因为,
所以,
同理可得:,
所以
,
(3)两种方案总样本均值的差为,
所以用方案二总体样本均值作为总体均值的估计不合适,原因是没有进行等比例的分层抽样,每个个体被抽到的可能性不同,因此代表性较差.
20.(1)0.9;(2),.
(1)由频数分布表得,课外阅读时间不少于12小时的共有10(名),即可求解样本中学生该周课外阅读时间少于12小时的频率;
(2)由频数分布表得,课外阅读时间落在[4,6)的人数为17,则频率是=0.17,进而可计算频率分布直方图中的值.
【详解】
(1)由频数分布表得,100名学生课外阅读时间不少于12小时的共有6+2+2=10(名),
所以样本中学生该周课外阅读时间少于12小时的频率P=1–=0.9;
则从该校随机选取一名学生,估计这名学生该周课外阅读时间少于12小时的频率是0.9;
(2)由频数分布表得,课外阅读时间落在[4,6)的人数为17,则频率是=0.17,
所以由频率分布直方图得,a==0.085,
同理可得,b==0.125.
本题主要考查了频率分布直方图的应用,其中解答中熟记在频率分布直方图中,各小长方形的面积表示相应各组的频率,所以所有小长方形的面积的和等于1,且每个小矩形的高度为是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
21.(1)频率分布直方图答案见解析,平均分;(2)分数线为99.
(1)作出频率分布直方图,结合频率分布直方图的性质能求出平均分.(2)由题可知,,的频率为0.04,,的频率为0.28,由此能求出英语成绩为优秀的分数线.
【详解】
解:(1)频率分布直方图如下:
平均分.
(2)由题可知,的频率为0.04,
的频率为0.28,
因为这100名学生英语成绩的优秀率为,所以成绩优秀的分数线在之间,
设优秀成绩的分数线为x,则有.1
解得.
故英语成绩为优秀的分数线为99.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在高一(1)班组织的“我爱古诗词”的调研考试中,全班40名学生的成绩数据(均为整数且都在)统计为如下的频率分布直方图,则第四小组(成绩分布在)的频率为( )
A.0.001 B.0.01 C.0.03 D.0.3
2.10名工人某天生产同一零件,生产的件数是15、17、14、10、15、17、17、16、14、12.设其平均数为a,中位数为b,众数为c,则有( )
A. B. C. D.
3.已知甲 乙两组数据(已按从小到大的顺序排列):甲组:27,28,39,40,m,50;乙组:24,n,34,43,48,52.若这两组数据的30百分位数 80百分位数分别相等,则等于( )
A. B. C. D.
4.2020年是脱贫攻坚战决胜之年凝心聚力打赢脫贫攻坚战,确保全面建成小康社会某县举行扶贫知识政策答题比赛,分初赛和复赛两个阶段进行规定:初赛成绩大于80分的进入复赛,某校有500名学生参加了初赛,所有学生的成绩均在区间内,其频率分布直方图如图所示,则进入复赛的人数为( )
A.125 B.250 C.375 D.400
5.某学校有160名教职工,其中教师120名,行政人员16名,后勤服务人员24名,今从中抽取一个容量为20的样本,采用( )较为合适.
A.简单随机抽样 B.系统抽样
C.分层抽样 D.其他抽样
6.为落实《国家学生体质健康标准》达标测试工作,全面提升学生的体质健康水平,某校高二年级体育组教师在高二年级随机抽取部分男生,测试了立定跳远项目,依据测试数据绘制了如图所示的频率直方图.已知立定跳远以上成绩为及格,以上成绩为优秀,根据图中的数据估计该校高二年级男生立定跳远项目的优秀率和图中的分别是是( )
A.3%,0.010 B.3%,0.012 C.6%,0.010 D.6%,0.012
7.甲、乙两支曲棍球队在去年的国际比赛中,甲队的平均每场进球数为,全年比赛进球个数的标准差为3;乙队的平均每场进球数为,全年比赛进球个数的标准差为.下列说法正确的个数为( )
①甲队的技术比乙队好; ②乙队发挥比甲队稳定;③甲队的表现时好时坏.
A.0 B.3 C.2 D.1
8.某学校组建了演讲,舞蹈 航模 合唱,机器人五个社团,全校名学生每人都参加且只参加其中一个社团,校团委从这名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为( )
A. B. C. D.
9.若干年前,某老师刚退休的月退休金为4000元,月退休金各种用途占比统计图如下面的条形图.该老师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该老师的月退休金为( )
A.5000元 B.5500元 C.6000元 D.6500元
10.我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,大数据的相关岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
数据开发 8% 25% 32% 35%
数据分析 15% 36% 32% 17%
数据挖掘 9% 12% 28% 51%
数据产品 7% 17% 41% 35%
由表中数据可得该市大数据相关的各类岗位的薪资水平高低情况为( )A.数据挖掘>数据开发>数据产品>数据分析 B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品 D.数据挖掘>数据产品>数据分析>数据开发
11.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
12.已知某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的平均数为,方差为,则( )
A., B.,
C., D.,
二、填空题
13.现凯里一中高一年级、高二年级、高三年级的学生人数分别是1500、2000、2500人,现用分层抽样方法在全校抽取一个容量为120人的样本,则高二年级应该抽_______人.
14.下列数据是30个不同国家中每100000名男性患某种疾病的死亡率:
27.0 23.9 41.6 33.1 40.6 18.8 13.7 28.9 13.2 14.5
27.0 34.8 28.9 3.2 50.1 5.6 8.7 15.2 7.1 5.2
16.5 13.8 19.2 11.2 15.7 10.0 5.6 1.5 33.8 9.2
这组数据的第40百分位数是________.
15.在用抽签法抽样时,有下列五个步骤:
(1)从箱中每次抽出1个号签,并记录其编号,连续抽取k次;
(2)将总体中的所有个体编号;
(3)制作号签;
(4)将总体中与抽到的签的编号相一致的个体取出构成样本;
(5)将号签放在同一箱中,并搅拌均匀.
以上步骤的次序是______________.
16.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为___________.
三、解答题
17.现有银川二中高一年级某班甲、乙两名学生自进入高中以来的历次数学成绩(单位:分),具体考试成绩如下:
甲:、、、、、、、、、、、、;
乙:、、、、、、、、、、、、.
(1)请你画出两人数学成绩的茎叶图;
(2)根据茎叶图,运用统计知识对两人的成绩进行比较.(最少写出两条统计结论)
18.治理沙漠离不开优质的树苗,现从苗圃中随机地抽测了200株树苗的高度(单位:cm),得到以下频率分布直方图.
(1)求直方图中a的值及众数 中位数;
(2)若树高185cm及以上是可以移栽的合格树苗.从样本中按分层抽样方法抽取20株树苗作进一步研究,不合格树苗 合格树苗分别应抽取多少株?
19.某校有高中生2000人,其中男女生比例约为,为了获得该校全体高中生的身高信息,采取了以下两种方案:方案一:采用比例分配的分层随机抽样方法,抽收了样本容量为的样本,得到频数分布表和频率分布直方图.方案二:采用分层随机抽样方法,抽取了男、女生样本量均为25的样本,计算得到男生样本的均值为170,方差为16,女生样本的均值为160,方差为20.
身高(单位:)
频数 6 4
(1)根据图表信息,求,并补充完整频率分布直方图,估计该校高中生的身高均值;(同一组中的数据以这组数据所在区间中点的值为代表)
(2)计算方案二中总样本的均值及方差;
(3)计算两种方案总样本均值的差,并说明用方案二总样本的均值作为总体均值的估计合适吗?为什么?
20.从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到频数分布表和频率分布直方图如下.
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18) 2
合计 100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率分布直方图中的a,b的值.
21.某校根据该校高一年级100名学生的英语成绩(不包括听力部分)得到如下频数分布表:
分组
频数 8 24 36 28 4
(1)根据频数分布表,作出这些数据的频率分布直方图,并求这100名学生英语成绩(不包括听力部分)的平均分(同一组中的数据用该组区间的中间值作代表);
(2)若这100名学生英语成绩的优秀率为,求英语成绩为优秀的分数线(保留整数位).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
根据频率之和为1可求出.
【详解】
由频率分布直方图可得第四小组的频率为.
故选:D.
2.B
将样本数据由小到大进行排列,根据定义求出,即可得出结论.
【详解】
解:将生产的件数由小到大排列为:10、12、14、14、15、15、16、17、17、17,
∴ ,中位数为,
众数为,
因此,,
故选:B.
3.A
根据百分位数的定义并结合已知条件求出的值,由此可得的值.
【详解】
因为×6=1.8,×6=4.8,所以30百分位数为第二个数,即n=28,80百分位数为第五个数即m=48,所以==.
故选:A
4.A
根据直方图求得成绩大于80分的频率,然后乘以总人数即得所求.
【详解】
由直方图可知,成绩大于80分的频率为,
又∵总人数为500人,所以进入复赛的人数为500×0.25=125,
故选:A.
本题考查直方图,关键是理解直方图的意义.
5.C
利用分层抽样的概念求解.
【详解】
由题知,学校教职工有3种类别,所以选用分层抽样较为合适.
故选:C.
6.C
根据频率分布直方图可直接求出优秀率,根据频率之和为,可求出.
【详解】
由频率分布直方图可得,优秀率为;
由,解得;
故选:C.
7.B
根据平均数、方差的知识,对四个说法逐一分析,由此得出正确选项.
【详解】
∵甲队平均数大于乙队的平均数,∴甲队的技术比乙队好,
又∵甲队的标准差大于乙队的标准差,∴乙队发挥比甲队稳定,甲队的表现时好时坏,故①②③都对.
故选:B
本题主要考查平均数、方差在实际生活中的应用,属于基础题.
8.B
根据演讲的人数,求得本次调查的人数为人,进而求得机器人所占的比例,即可求解.
【详解】
由题意,本次调查的人数为人,
其中合唱比赛所占的比例为,
所以机器人所占的比例为,
所以选取的学生中参加机器人社团的学生数为人.
故选:B.
9.A
根据条形图计算出刚退休时就医费用,进而计算出现在的就医费用,结合目前就医费用所占退休金的比例可得出结果.
【详解】
刚退休时就医费用为元,现在的就医费用为元,占退休金的,
因此,目前该教师的月退休金为元.
故选:A
10.B
根据题意和表格的数据分别计算数据开发、数据分析、数据产品的平均薪资,进而比较大小即可.
【详解】
由题中选项知数据挖掘的平均薪资最高,故只需计算并比较其他三类工作岗位的平均薪资.估计数据开发的平均薪资为;
估计数据分析的平均薪资为;
估计数据产品的平均薪资为.
故数据挖掘>数据产品>数据开发>数据分析.
故选:B.
11.A
可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】
设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
12.A
由题设条件,利用平均数和方差的计算公式计算即可求解.
【详解】
设7个数为,
则,
,
所以,
所以,
则这个数的平均数为,
方差为.
故选:A.
13.40
由样本与总体所占比例相等可得.
【详解】
设高二年级应该抽取人,则,解得.
故答案为:40.
14.13.75
将数据从小到大排列,由,所求数为第12和第13两数的平均数.
【详解】
将数据按从小到大排列为
1.5 3.2 5.2 5.6 5.6 7.1 8.7 9.2
10.0 11.2 13.2 13.7 13.8 14.5 15.2 15.7
16.5 18.8 19.2 23.9 27 27 28.9 28.9
33.1 33.8 34.8 40.6 41.6 50.1
,
这组数据的第40百分位数是.
故答案为:
本题考查求百分位数,属于基础题.
15.(2)(3)(5)(1)(4)
按照抽签法的步骤判断,即编号,做号签,放入容器,进行抽取,构成样本.
【详解】
利用抽签法第一步要进行编号,然后做号签,放入容器,接下来按照逐个不放回地抽取号签,最后将与编号一致的个体取出构成样本,故这些步骤的先后顺序为(2)(3)(5)(1)(4).
故答案为:(2)(3)(5)(1)(4).
16.0.98.
本题考查通过统计数据进行概率的估计,采取估算法,利用概率思想解题.
【详解】
由题意得,经停该高铁站的列车正点数约为,其中高铁个数为10+20+10=40,所以该站所有高铁平均正点率约为.
本题考点为概率统计,渗透了数据处理和数学运算素养.侧重统计数据的概率估算,难度不大.易忽视概率的估算值不是精确值而失误,根据分类抽样的统计数据,估算出正点列车数量与列车总数的比值.
17.(1)图见解析
(2)答案见解析
(1)直接按照茎叶图定义画出即可;
(2)通过中位数、平均数、方差依次比较.
(1)
甲、乙两人数学成绩的茎叶图如图所示:
(2)
①从整体分析:乙同学的得分情况是大致对称的,中位数是;甲同学的得分情况,也大致对称,中位数是;
②平均分的角度分析:甲同学的平均分为,
乙同学的平均分为,乙同学的平均成绩比甲同学高;
③方差(稳定性)的角度:乙同学的成绩比较稳定,总体情况比甲同学好.
18.(1),众数为,中位数
(2)7株和13株
(1)利用频率分布直方图的性质及众数 中位数的求法即得;
(2)利用直方图及分层抽样方法即得.
(1)
∵,
∴,众数为,
设中位数为x,因为,
,
则,
,
∴
故,众数为,中位数.
(2)
由题可知合格树苗所占频率为,不合格树苗所占频率为,
不合格的抽取株,合格的抽取株,
故不合格树苗 合格树苗分别应抽取7株和13株.
19.(1),,频率分布直方图见解析,身高均值(2)均值为,方差为;(3)总样本均值的差为,不合适,理由见解析.
(1)利用身高在区间的频率和频数即可求的值,进而可得的值,求出各组的频率即可补全频率分布直方图,由平均数的计算公式即可求身高均值;
(2)把男生样本记为:,其均值为,方差为,把女生样本记为:,其均值为,方差为,则总体样本均值为,
根据方差公式和平均数公式变形即可得样本总体方差.
(3)两个方案的均值相减即可求均值差,由于没有进行等比例的分层抽样,每个个体被抽到的可能性不同,代表性较差,因此不合适.
【详解】
(1)因为身高在区间的频率为,频数为,
所以样本容量为,,,
,
所以身高在的频率为,小矩形的高为,
所以身高在的频率为,小矩形的高为,
由此补全频率分布直方图:
由频率分布直方图可知:样本的身高均值为:
,
所以由样本估计总体可知,估计该校高中生的身高均值为
(2)把男生样本记为:,其均值为,方差为,
把女生样本记为:,其均值为,方差为,
总体样本均值记为,方差记为,
所以,
又因为,
所以,
同理可得:,
所以
,
(3)两种方案总样本均值的差为,
所以用方案二总体样本均值作为总体均值的估计不合适,原因是没有进行等比例的分层抽样,每个个体被抽到的可能性不同,因此代表性较差.
20.(1)0.9;(2),.
(1)由频数分布表得,课外阅读时间不少于12小时的共有10(名),即可求解样本中学生该周课外阅读时间少于12小时的频率;
(2)由频数分布表得,课外阅读时间落在[4,6)的人数为17,则频率是=0.17,进而可计算频率分布直方图中的值.
【详解】
(1)由频数分布表得,100名学生课外阅读时间不少于12小时的共有6+2+2=10(名),
所以样本中学生该周课外阅读时间少于12小时的频率P=1–=0.9;
则从该校随机选取一名学生,估计这名学生该周课外阅读时间少于12小时的频率是0.9;
(2)由频数分布表得,课外阅读时间落在[4,6)的人数为17,则频率是=0.17,
所以由频率分布直方图得,a==0.085,
同理可得,b==0.125.
本题主要考查了频率分布直方图的应用,其中解答中熟记在频率分布直方图中,各小长方形的面积表示相应各组的频率,所以所有小长方形的面积的和等于1,且每个小矩形的高度为是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
21.(1)频率分布直方图答案见解析,平均分;(2)分数线为99.
(1)作出频率分布直方图,结合频率分布直方图的性质能求出平均分.(2)由题可知,,的频率为0.04,,的频率为0.28,由此能求出英语成绩为优秀的分数线.
【详解】
解:(1)频率分布直方图如下:
平均分.
(2)由题可知,的频率为0.04,
的频率为0.28,
因为这100名学生英语成绩的优秀率为,所以成绩优秀的分数线在之间,
设优秀成绩的分数线为x,则有.1
解得.
故英语成绩为优秀的分数线为99.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
